二叉排序树的删除

code

#include <bits/stdc++.h>

using namespace std;

const int ENDFLAG = -1; //输入结束的标志

typedef struct
{
    int key; //关键字
    int otherinfo; //其他数据项
}ElemType;

istream& operator >>(istream &is, ElemType& e)
{
    cin >> e.key >> e.otherinfo;
    return is;
}

typedef struct BSTNode
{
    ElemType data; //数据域
    struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;

//当树中不存在关键字等于key的节点时才进行插入
//且新插入的节点一定是一个新添加的叶子节点。
void InsertBST(BSTree &T, ElemType e)
{
    if (T == NULL) //找到插入位置，递归结束
    {
        BSTNode *s = new BSTNode; //生成新的节点*s
        s->data = e; //将新节点的数据域置为e
        s->lchild = s->rchild = NULL; //将新节点的左右子树置为空
        T = s; //把新节点*s连接到已找到的插入位置
    }
    else if (e.key < T->data.key)
        InsertBST(T->lchild, e); //将*s插入左子树
    else
        InsertBST(T->rchild, e); //将*s插入右子树
}

void CreateBST(BSTree &T)
{
    T = NULL;
    ElemType e;
    cin >> e;
    while (e.key != ENDFLAG)
    {
        InsertBST(T, e);
        cin >> e;
    }
}

BSTNode* SearchBST(BSTree T, int key)
{
    if (T == NULL || key == T->data.key) return T; //查找结束，如果失败则返回空指针，成功则返回该指针
    else if (key < T->data.key) return SearchBST(T->lchild, key); //递归查找左子树
    else return SearchBST(T->rchild, key); //递归查找右子树
}

void inorder(BSTree T)
{
    if (T)
    {
        inorder(T->lchild);
        cout << T->data.key << " ";
        inorder(T->rchild);
    }
}

void DeleteBST(BSTree &T, int key)
{
    BSTNode *p = T;
    BSTNode *f = NULL;
    //查找被删节点p及其父节点f
    while (p)
    {
        if (p->data.key == key) break;
        f = p; //*f为*p的父节点
        if (key < p->data.key) p = p->lchild;
        else p = p->rchild;
    }
    if (p == NULL) return; //没找到被删节点，结束
    ///对被删节点p进行处理
    BSTNode *q = p; //将被删节点p用q暂存
    //第一种情况：p的左右子树均不为空
    if ((p->lchild) && (p->rchild))
    {
        //在p的左子树中查找其直接前驱节点，即最右下点
        BSTNode *s = p->lchild;
        while (s->rchild)
        {
            //向右走到尽头
            q = s;
            s = s->rchild;
        }
        p->data = s->data; //将p节点的值改为s节点的值
        //删除s节点
        //注意：因为s为最右下的点，所以s只有左子树
        if (q != p) q->rchild = s->lchild; //q的右子树等于s的左子树
        else q->lchild = s->lchild; //q的左子树等于s的左子树
        delete s;
        return;
    }
    //第二种情况：p的右子树为空。只需重接左子树
    else if (p->rchild == NULL)
    {
        p = p->lchild;
    }
    //第三种情况：p的左子树为空，只需重接右子树
    else if (p->lchild == NULL)
    {
        p = p->rchild;
    }
    //将p所指向的子树挂接到其父节点*f相应的位置上
    if (f == NULL) //被删节点为根节点
        T = p;
    else if (q == f->lchild) //被删节点是父节点的左儿子
        f->lchild = p; //挂接到f的左子树的位置上
    else //被删节点是父节点的右儿子
        f->rchild = p; //挂接到f的右子树的位置上
    delete q;
}

int main()
{
    BSTree T;
    CreateBST(T);
    int x;
    cin >> x;
    printf("要删除的元素是%d\n", x);
    printf("删除%d之前对%d的查询结果如下：\n", x, x);
    BSTNode *s = SearchBST(T, x);
    if (s == NULL) puts("Not Found!");
    else cout << "s->data.key = " << s->data.key << endl;
    puts("此时的先序遍历结果：");
    inorder(T);
    cout << endl;
    DeleteBST(T, x);
    printf("删除%d之后对%d的查询结果如下：\n", x, x);
    s = SearchBST(T, x);
    if (s == NULL) puts("Not Found!");
    else cout << "s->data.key = " << s->data.key << endl;
    puts("此时的先序遍历结果：");
    inorder(T);
    return 0;
}

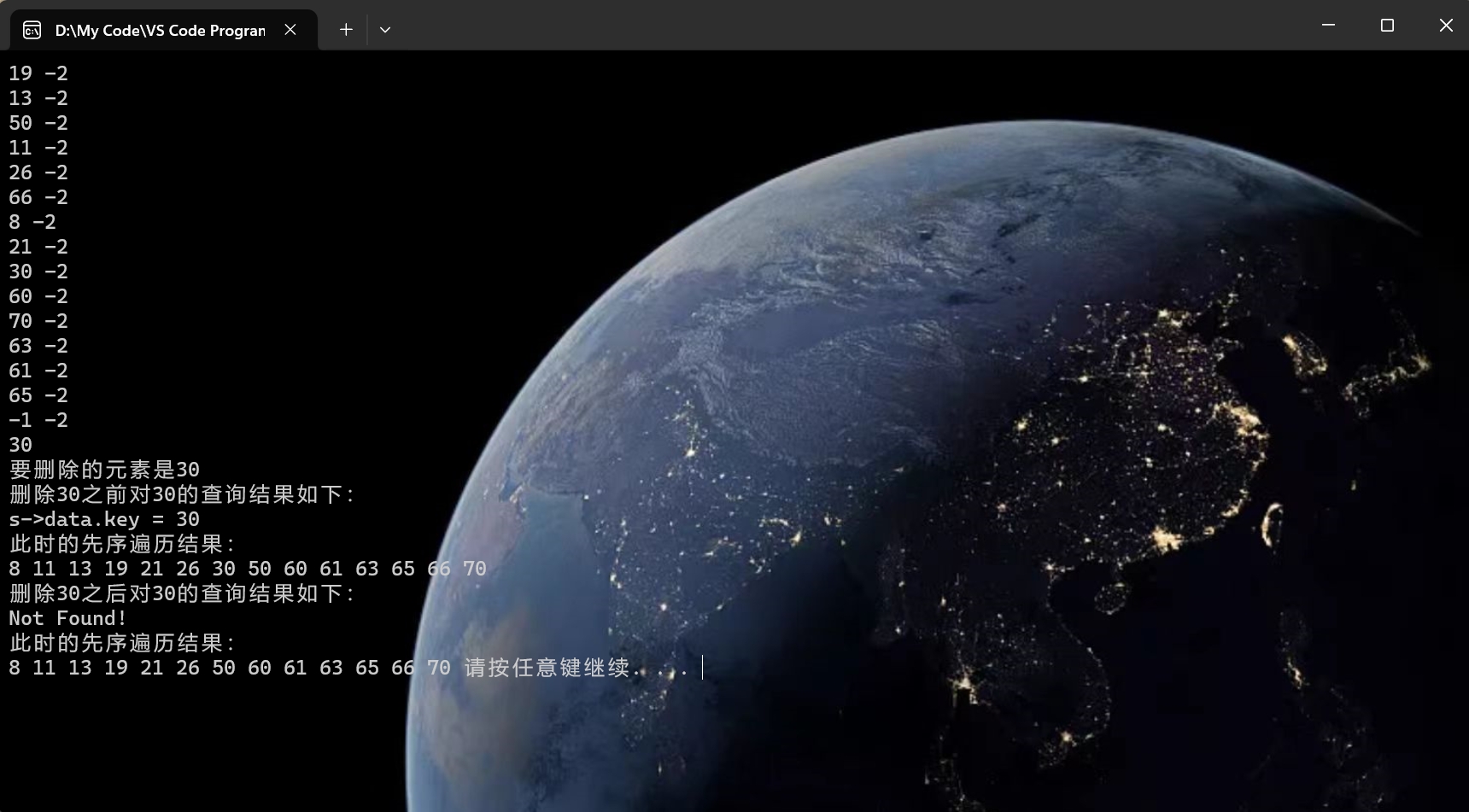
运行结果