图的邻接矩阵--Dijkstra算法

图的邻接矩阵--**Dijkstra算法**
//代码附有详细注释
完整代码在我的资源中有。

常量，用于表示图中的无穷（max）和顶点个数（n）
不同的图对应不同的顶点个数。

#define max 1000
#define n 5

方便理解的别名，代码越长越有优势

typedef int Graph[n][n]; //图
//typedef <元素类型关键字><数组类型名>[<常量表达式1>][<常量表达式2>]
typedef int vertex; //顶点 

 

算法核心
G为已存在的图，v表示源点，dist数组用于辅助查找搜索

void shortp(Graph G, vertex v, int dist[n])
//源点v
//dist[n]表示当前所找到的从源点v到终点Vi的最短路径长度
{
int i, wmin, u, S[n];
//wmin代表一次搜索过程中最小值，u代表其最小值指向的顶点
int num=1;
for (i=0; i<n; i++)//数组dist及集合S赋初值
{
dist[i]=G[v][i];
S[i]=0; 
}
S[v]=1; //把顶点v加入集合S中,1表示在集合S当中，0表示不在集合S中
do{
wmin=max; 
u=v;
for(i=0; i<n; i++) //选择顶点u
{
if (S[i] == 0) //不在集合S中的顶点
{
if (dist[i] < wmin) //找到最小值及其顶点
{
u=i;
wmin=dist[i];
}
}
}
S[u]=1; //把找到的顶点加入到集合S中
for (i=0; i<n; i++) 
{
if (S[i] == 0) //不在集合S中的顶点
{
if (dist[u]+G[u][i] < dist[i]) //u为最小值指向的顶点，dist[u]+G[u][i]表示从源点v0先到顶点u再到其他顶点的路径，dist[i]表示从源点v0直接到其他顶点的路径
dist[i]=dist[u]+G[u][i]; //取两者最小的作为源点v0直接到其他顶点的路径
}
}
num++;
}while (num != n-1);
}

 

主函数用于测验，图设置为有向网图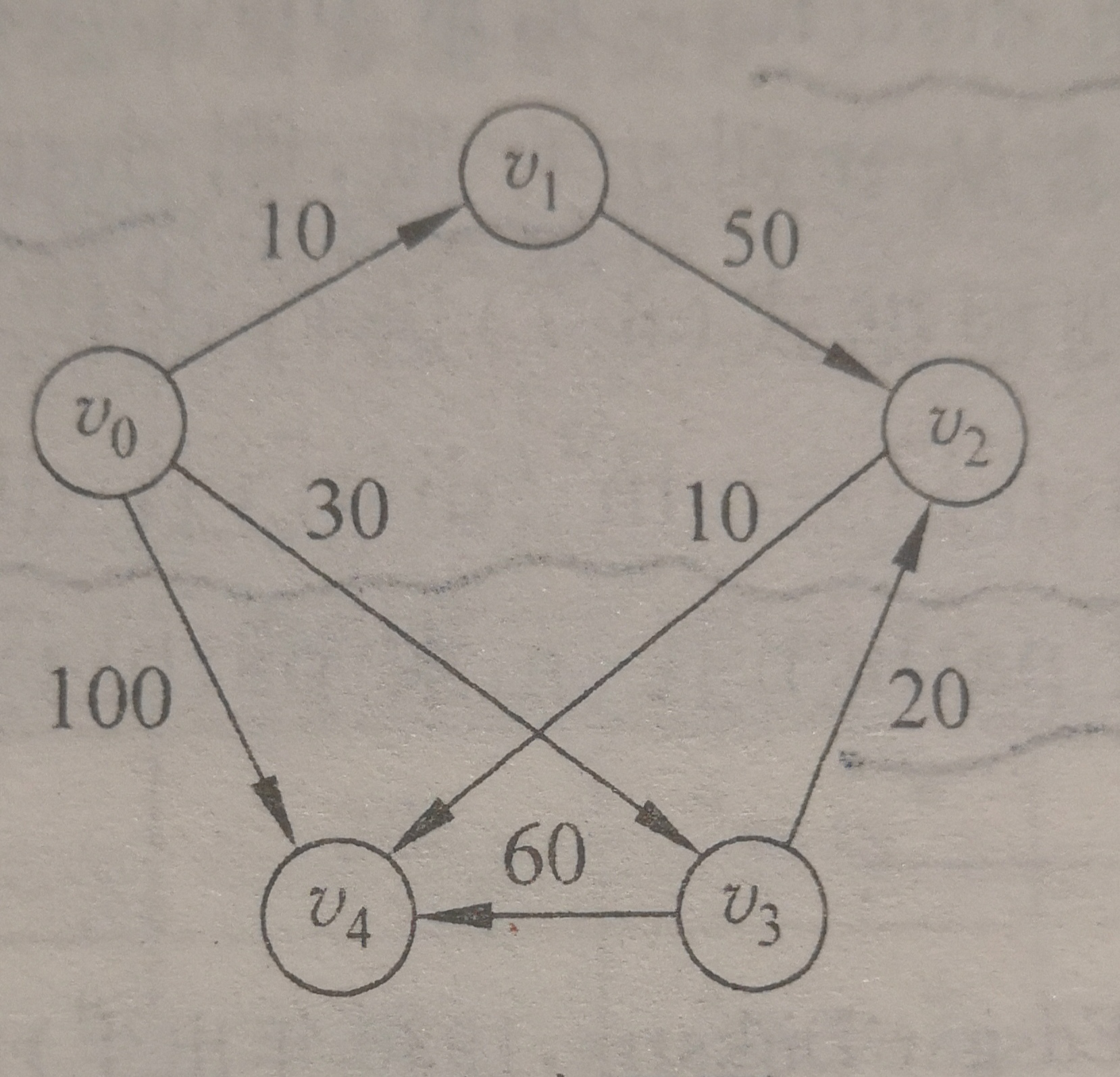

void main()
{ 
Graph G={
{ 0, 10,10000, 30, 100},
{10000, 0, 50,10000,10000},
{10000,10000, 0,10000, 10},
{10000,10000, 20, 0, 60},
{10000,10000,10000,10000, 0}}; 
vertex v=0; //源点v
int dist[n], i, j;
printf("please input weight of Graph ( 10000 is NaN ):\n"); 
for(i=0; i<n; i++)
{
for(j=0; j<n; j++)    printf("%5d ", G[i][j]);
printf("\n");
}
printf("\n");
shortp(G, v, dist);
for (i=0; i<n; i++) 
if (i != v)
printf("the shortest path of v[%d]->[%d] is:%d\n",v,i,dist[i]);
printf("\n");
}

最后，如果觉得这篇博客能帮助到你，请点赞、关注、收藏，后续我会持续更新，谢谢。