概率论与数理统计
概率论与数理统计
第一讲 随机事件与概率
1.1 随机事件
知识点


例题

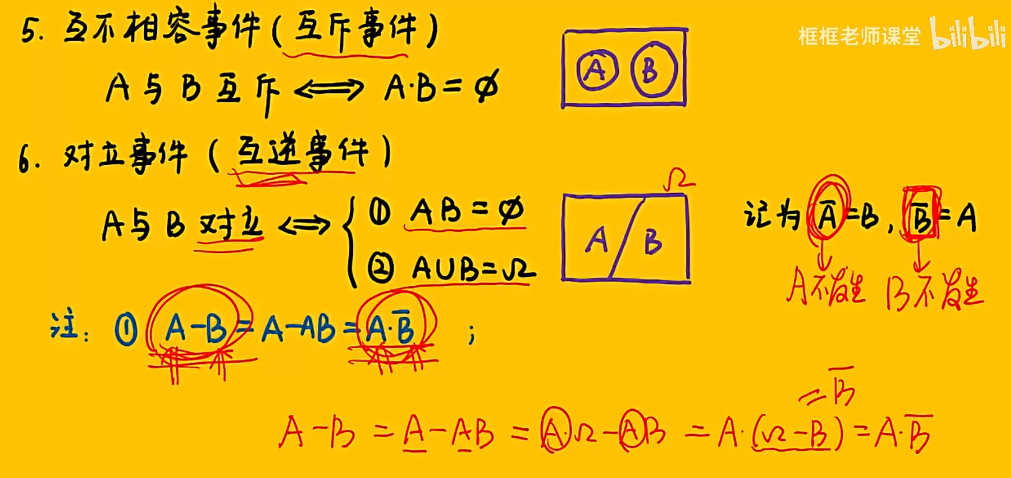
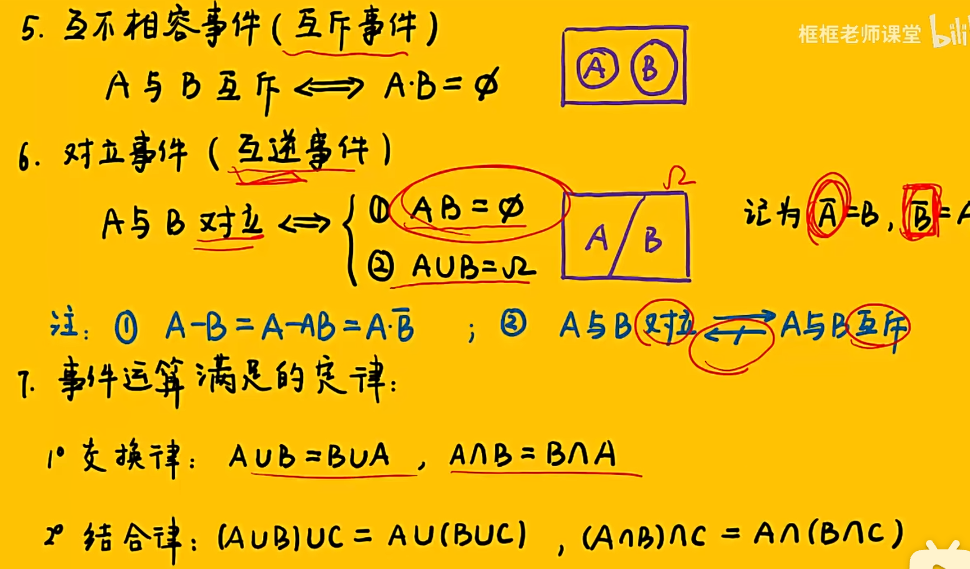
1.2 事件间的关系与运算
知识点

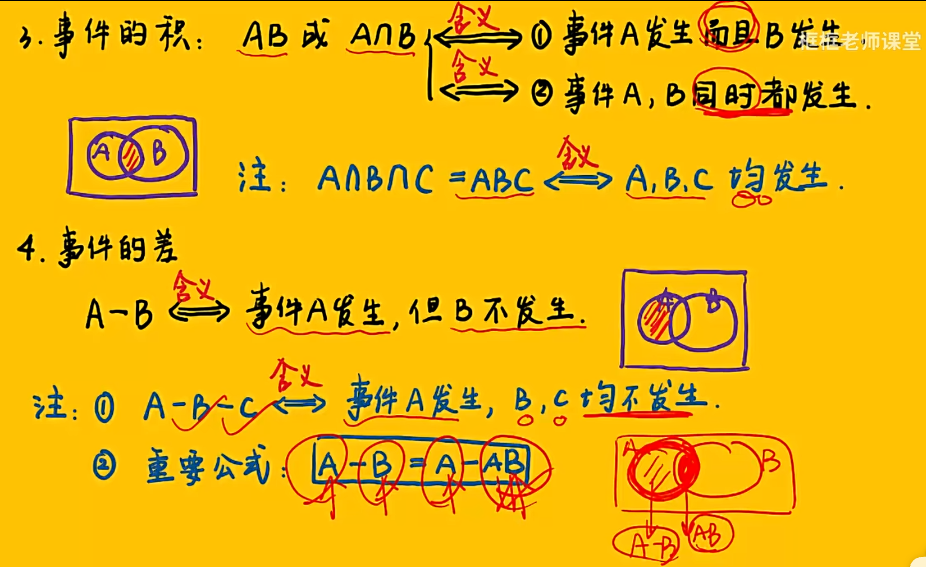
注:重要公式——被减数 - 减数 = 被减数 - 两者的交集 (在集合或事件的运算中总是成立)

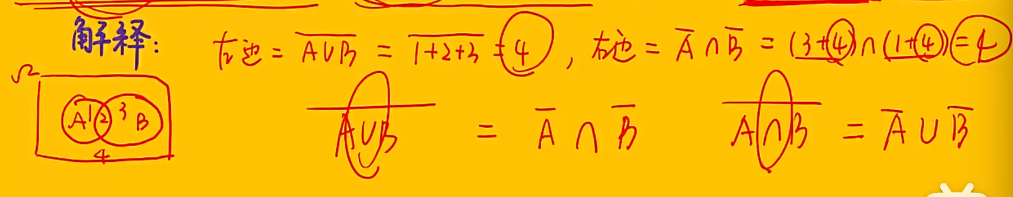
例题

1.3 概率的定义与性质
知识点


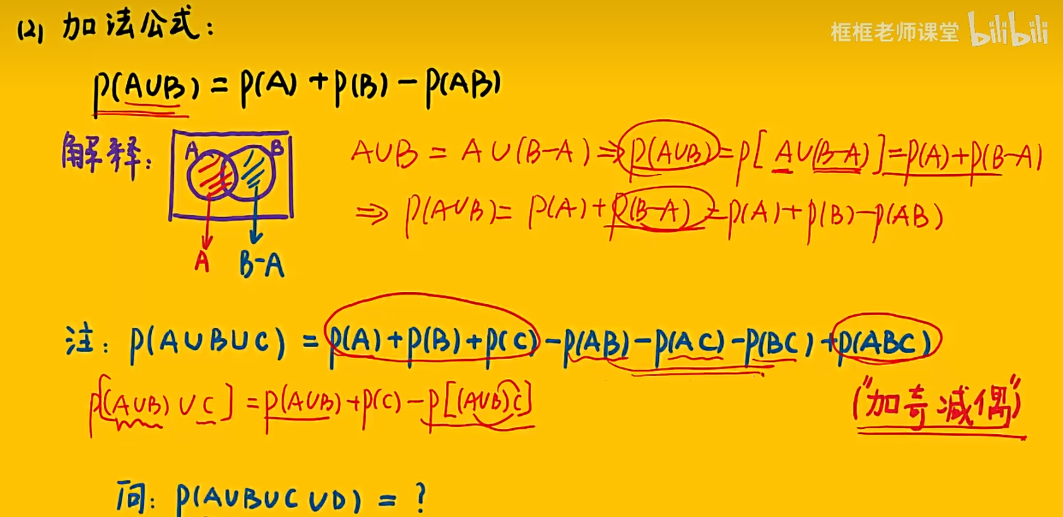
例题



1.4 古典概型
知识点

排列和组合
排列公式

组合公式

例题



1.5 几何概型
知识点

例题


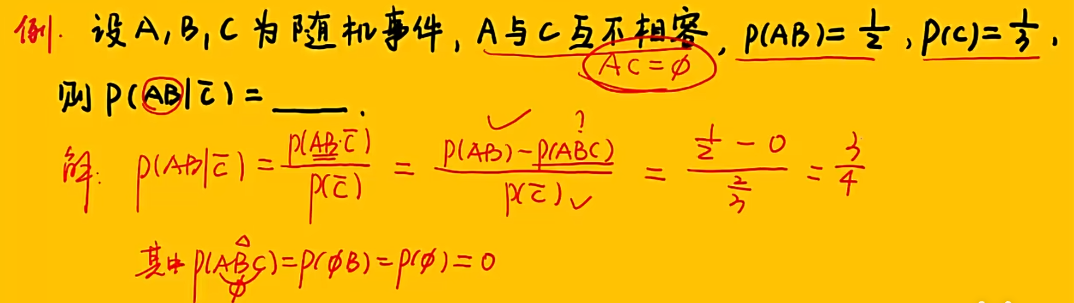
1.6 条件概率与乘积公式
知识点

注:公式4——忽略后面的A,P(B∪C) = P(B) + P(C) -P(BC),然后加入A;
公式5同理——忽略A,P(B-C) = P(B) - P(BC);
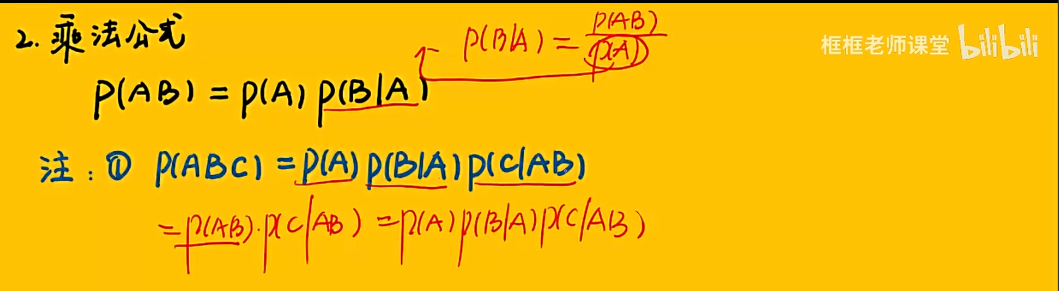
注:P(ABC)——第一步让A发生,第二步让B发生,但A已经发生,因此是P(B|A),第三步让C发生,但AB已经发生,因此是P(C|AB);
例题
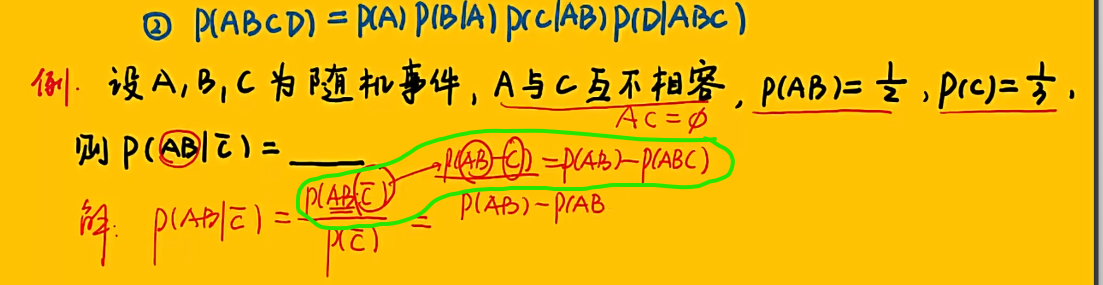

注:三事件——“第1此通过”、“第1次未过,第2次通过”、“前2次均未过,第3次通过”为互斥事件,因此互斥事件的概率 = 各事件概率的和;

1.7 全概率公式与贝叶斯公式
知识点

注:划分,又称为完备事件组;

注:由右下角图可知,BA1与BA2之间互斥,因此BA1,BA2,BA3······BAn是完备事件组;

注:贝叶斯公式,又称为逆概公式;
贝叶斯公式本质:已知一个复杂事件B发生的前提条件下,第j个小划分(完备)事件发生的条件概 率;
逆概公式原因:已知一个复杂事件发生的前提下,反过来求其中一个小划分(完备)事件发生的条件概率;

注:因为划分不唯一,因此要找到适合该应用题的一个划分;
例题

注:凡是涉及到复杂事件的概率,需要考虑用全概率公式;而第一步就是要找到适合于本题的一个划分——分阶段;

注:已知复杂事件发生的条件下, 问事件发生原因,需要考虑用贝叶斯公式;
1.8 事件的独立性
知识点


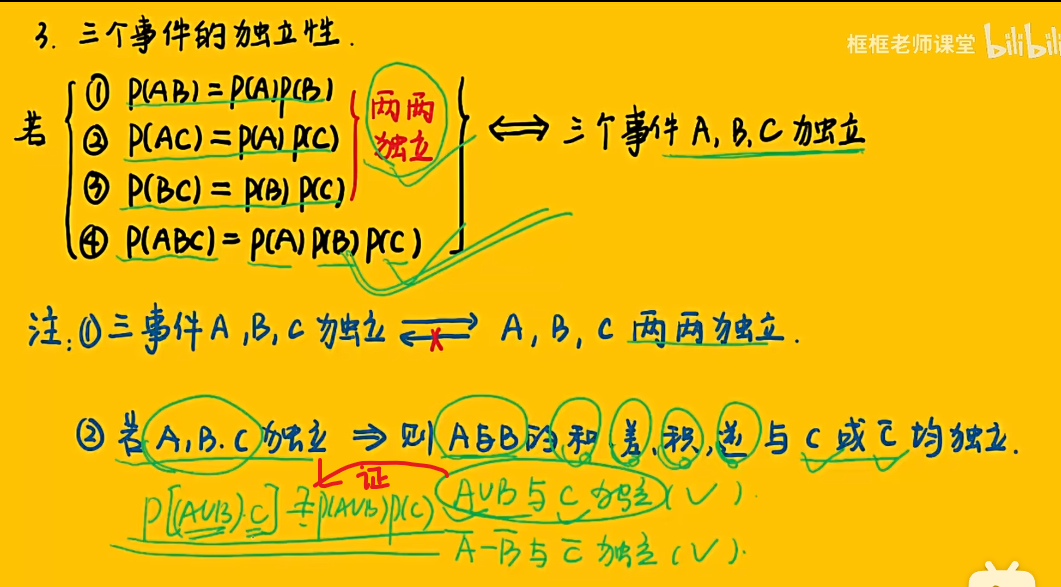
例题

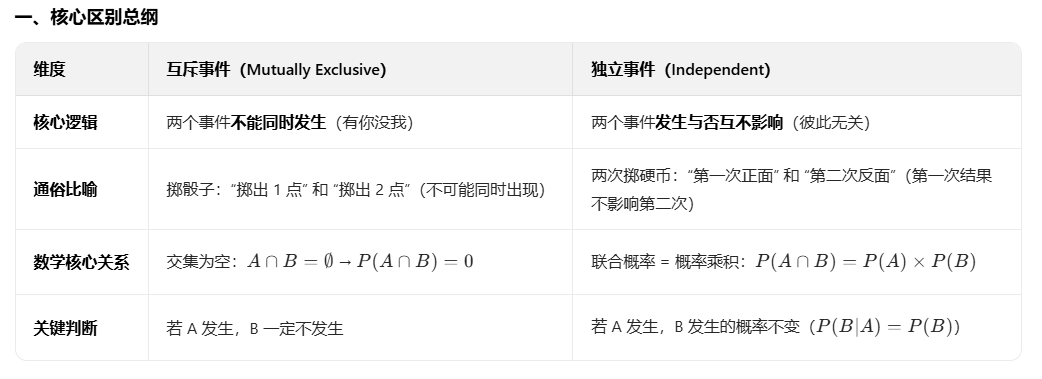
注:独立 ≠ 互斥



1.9 伯努利概型
知识点


例题


第二讲 随机变量及其分布
2.1随机变量与分布函数
知识点





例题


2.2 离散型随机变量及其分布
知识点


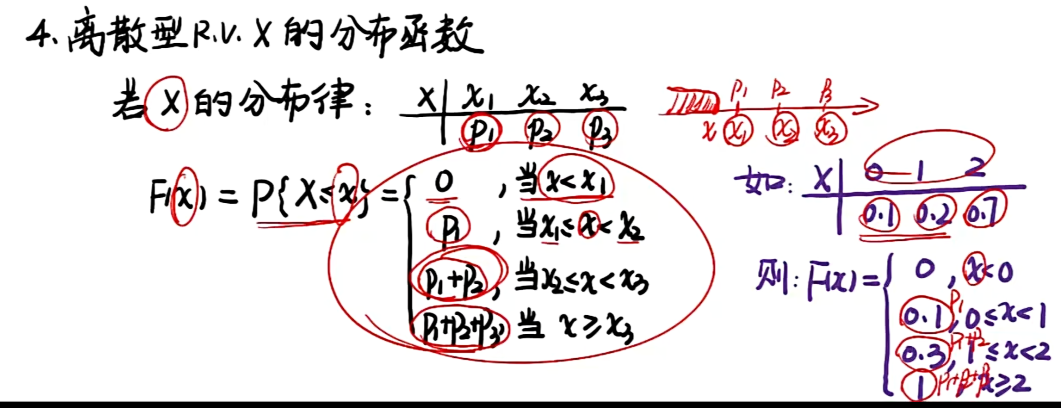
注:仅X1,X2,X3三个点上有概率,其余区域无;
例题


注:X=0,1,2,3最后一个1/2是不能通过的概率,X=4中的所有1/2是允许通过的概率;
知识点

注:二项分布的基础是 伯努利试验;

注:
-
泊松分布中λ 是单位时间 / 空间内事件的平均发生次数;
-
泊松分布的期望和方差相等,均为 λ;
-
泊松分布与二项分布的关系,见下图



例题

例题解释,如下图



2.3 连续型随机变量及其分布
知识点


注:规范性解释,如下图:

例题





知识点

注:①的解释是使用了上述例题的秒杀法;
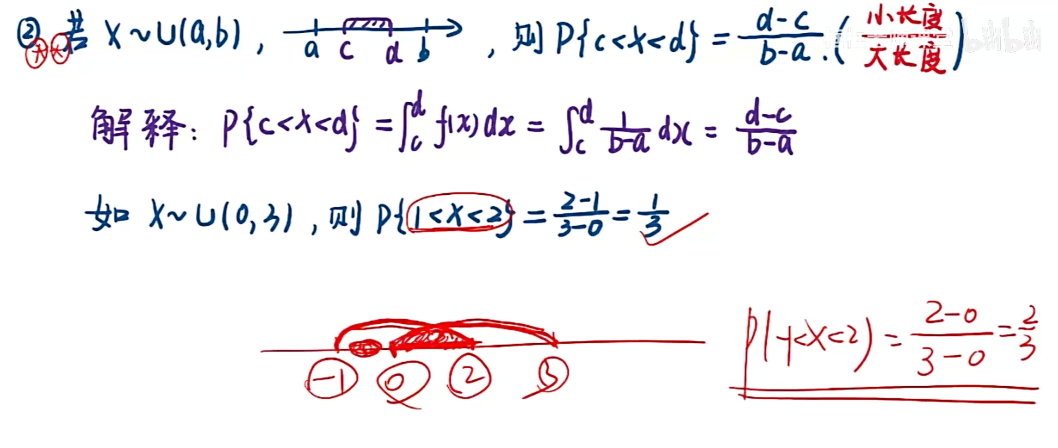
注:下方红字示例——无论小长度还是大长度,必须保证是有效长度;


注:举例——一个老电池使用t0个小时的情况下,它再使用T个小时的概率 = 一个新电池直接使用T个小时的概率

注:分子中交集,本质上是区间,“大大取大”,因此取P{x>t0+T},然后用秒杀公式;
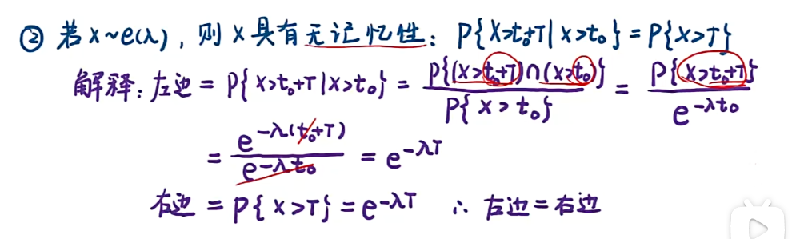
例题
均匀分布

注:十字交叉相乘法,如下图

指数分布
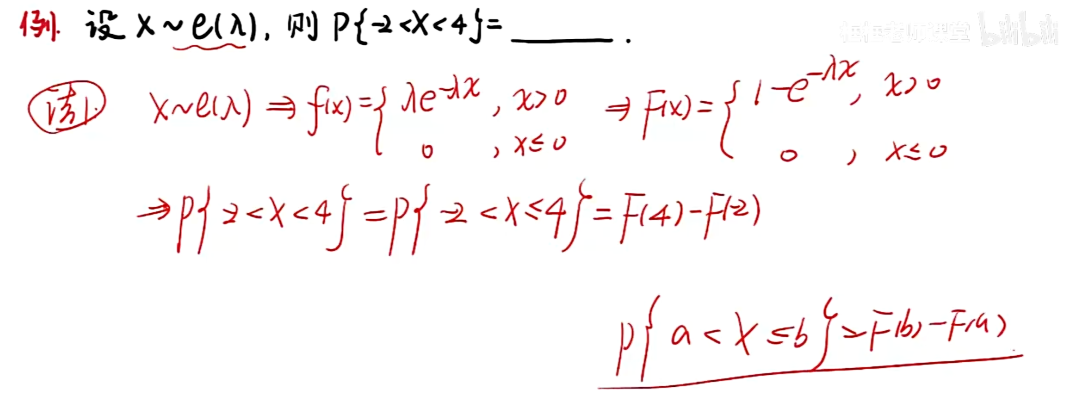
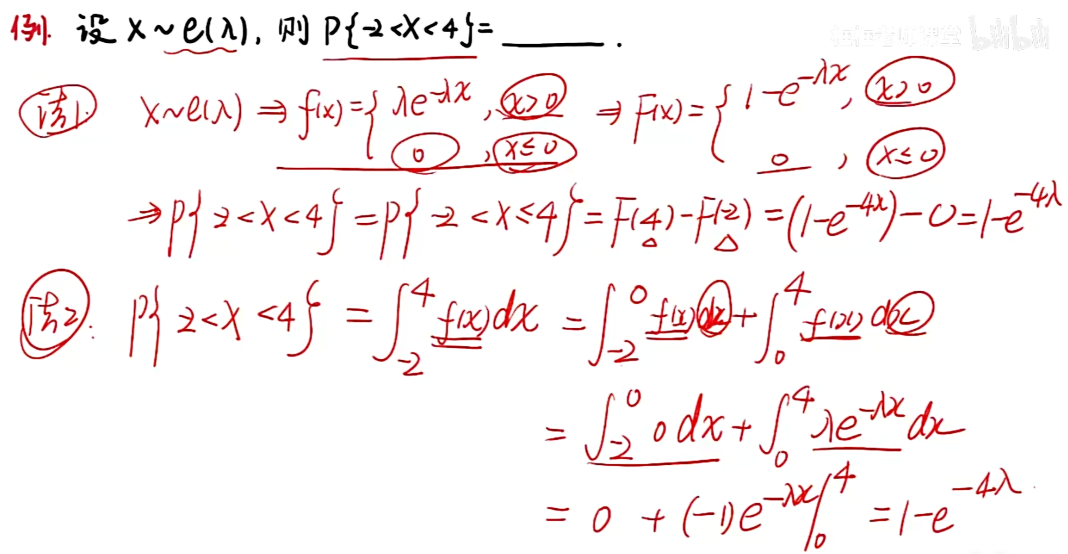
知识点
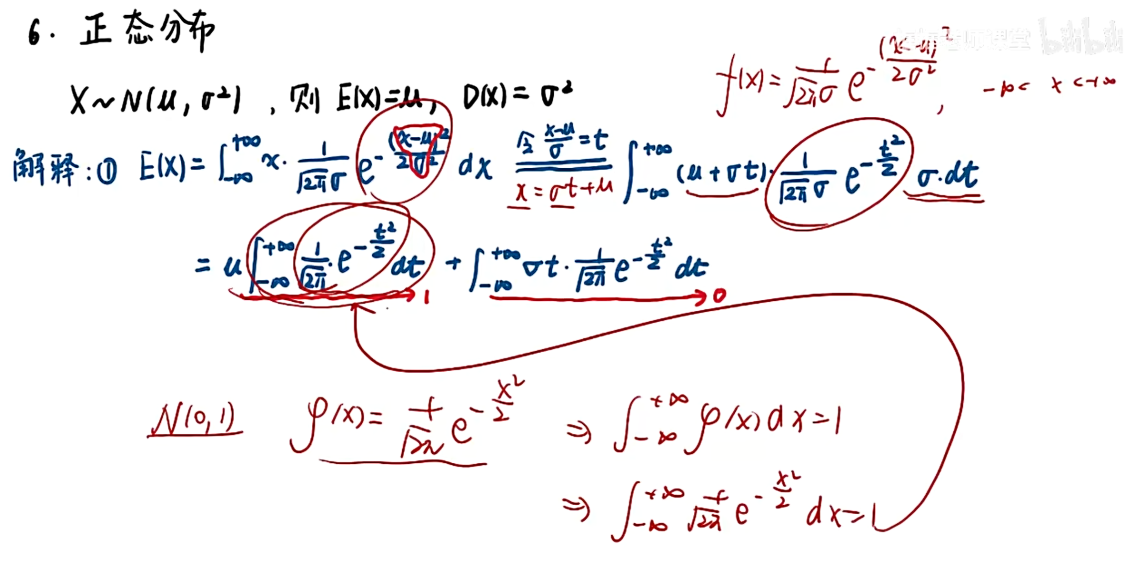
正态分布
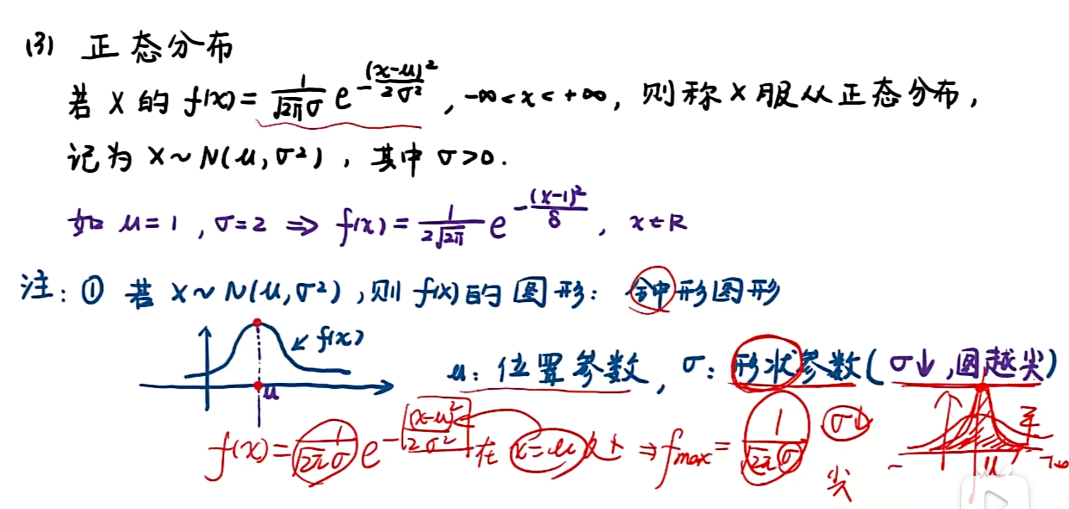
注:δ越小,图越尖,原因——δ越小,fmax变大,要保证图形面积为1(+∞,-∞对f(x)的积分为1),图会变尖;


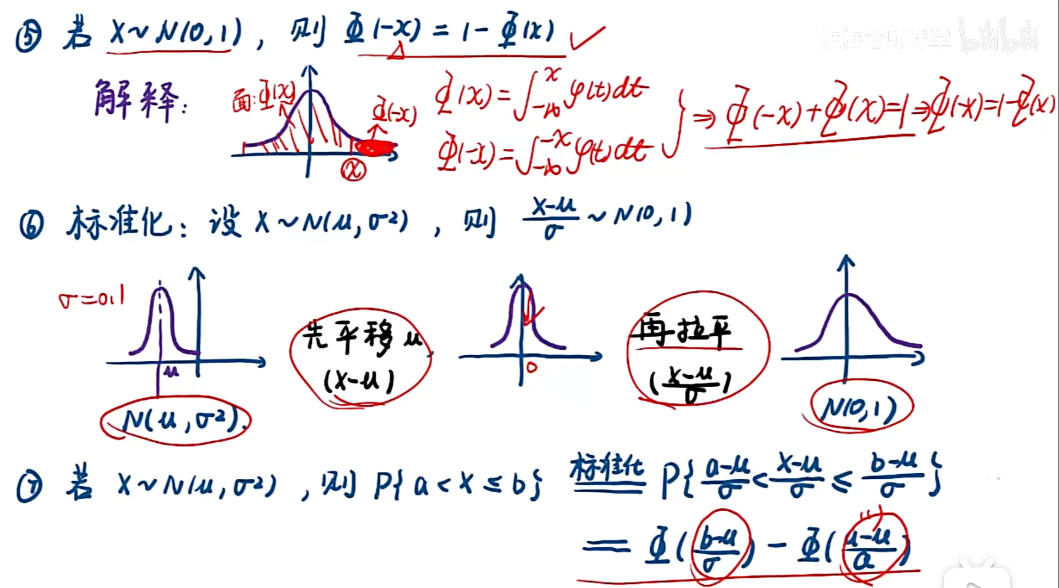
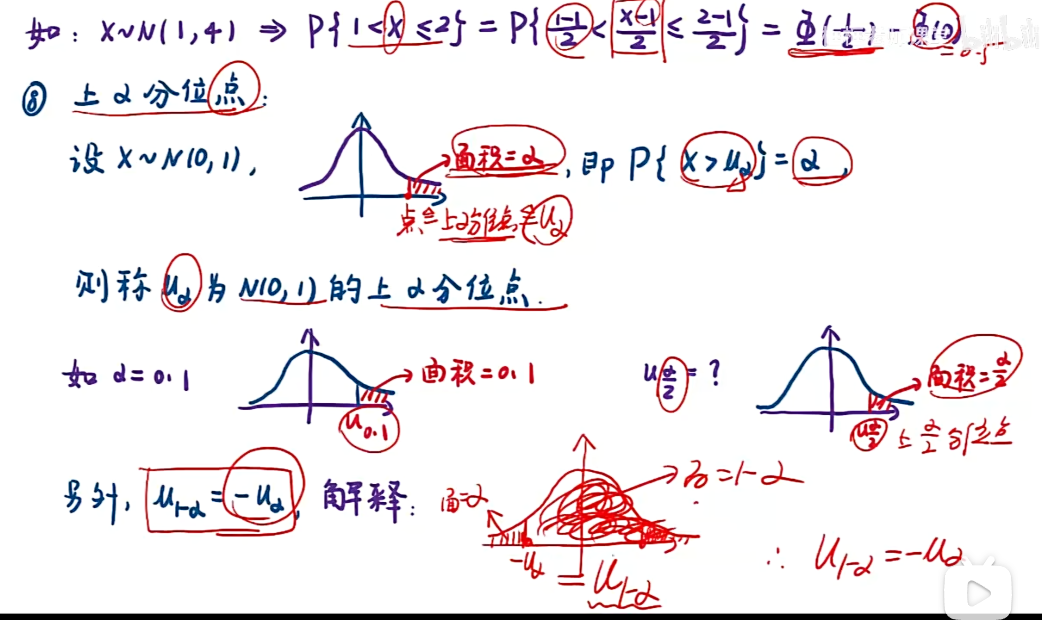
注:在连续条件下,概率 = 面积;
例题


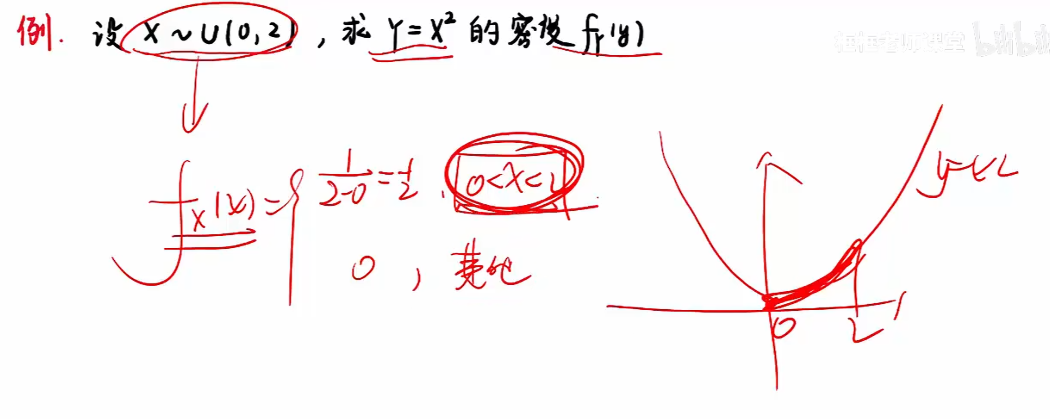
2.4 随机变量函数的分布
知识点


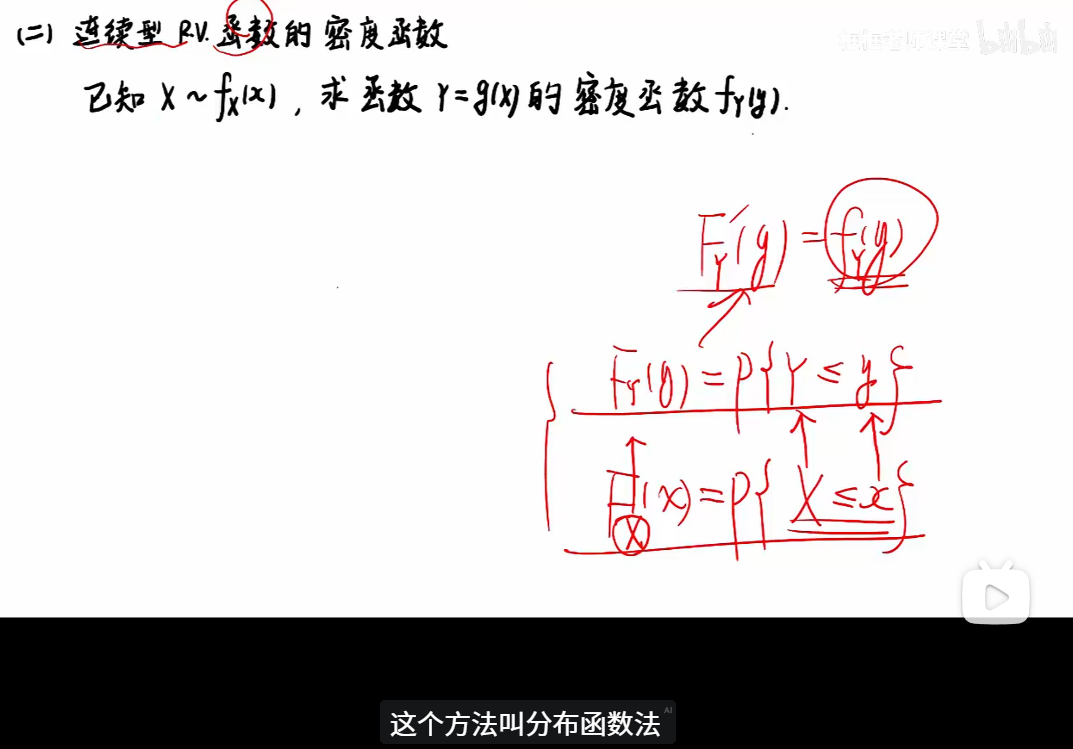


例题


注:一般求密度时,有效区间可以取成开区间,因此8 ≤ y可以改为8 < y, 把等号放入其他中;

注:
-
公式法的前提是 y = g(x) 具有单调性;
-
h`(y)取绝对值,是因为密度天然具有非负性;h(y)与y = g(x)同单调;
例题


注:满足公式法前提条件:单调;

注:如果不单调,检查其在有效区间上是否单调,如果单调,则可用公式法;


第三讲 多维随机变量及其分布
3.1 二维随机变量及其分布函数
知识点


注:无论X < -∞还是 Y < -∞,均是不可能事件,为空集;

例题

3.2 二维离散型R.V及其分布
知识点


例题


注:
P12中最后的C12表示从要放的两封信选出一封信,乘以1表示放入2号邮箱只有一种放法,后面乘以2表示放入3号或4号邮箱;
P13中将2封信捆绑成一个包,因此放法只有一种,分子为1;
3.3 二维连续型R.V及其分布
知识点

注:积分变量与字母无关,因此u,v可以变换为x,y;
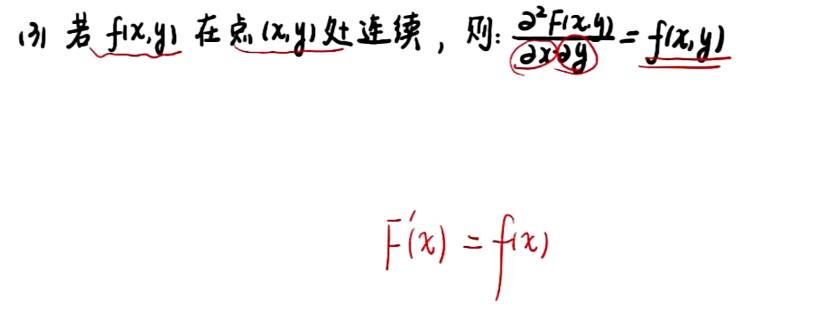
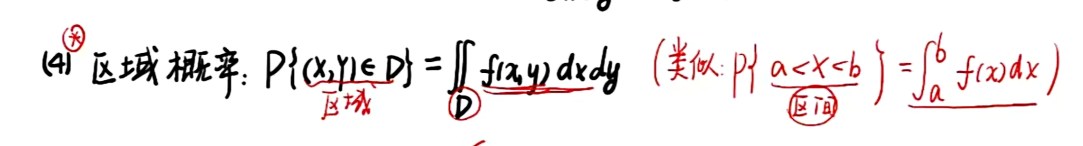
例题
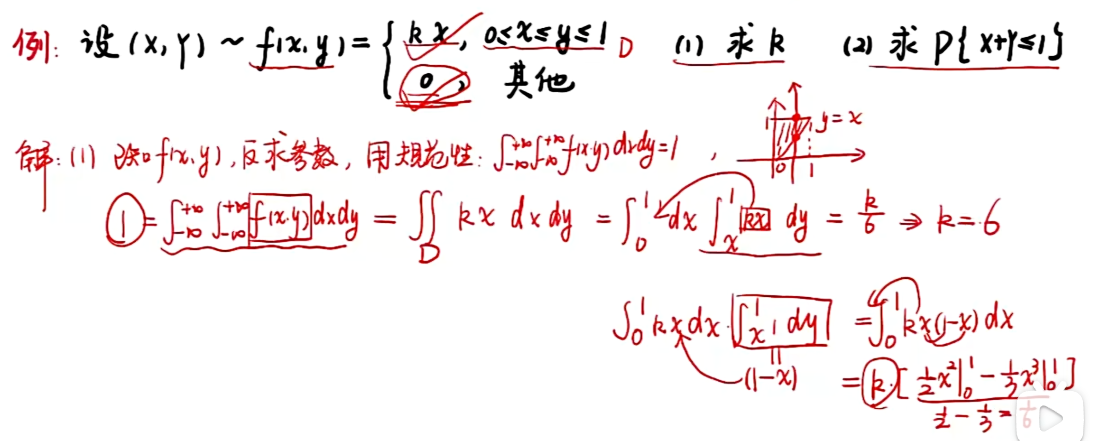


注:因为题中定义x > 0, y > 0, 将x,y看做u,v,则u > 0, v > 0;因此只有当(x,y)落在第一象限时,才会出现交集;
知识点

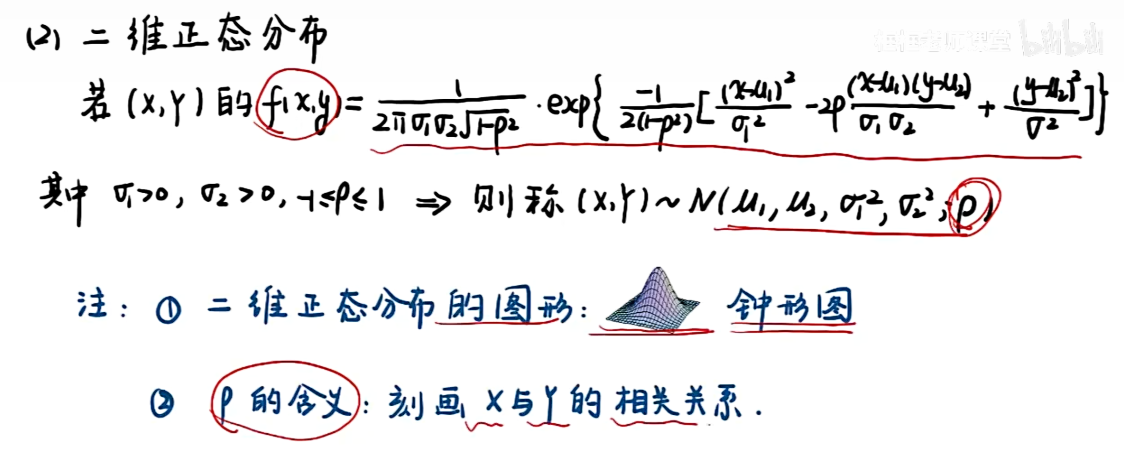
3.4 边缘分布
知识点



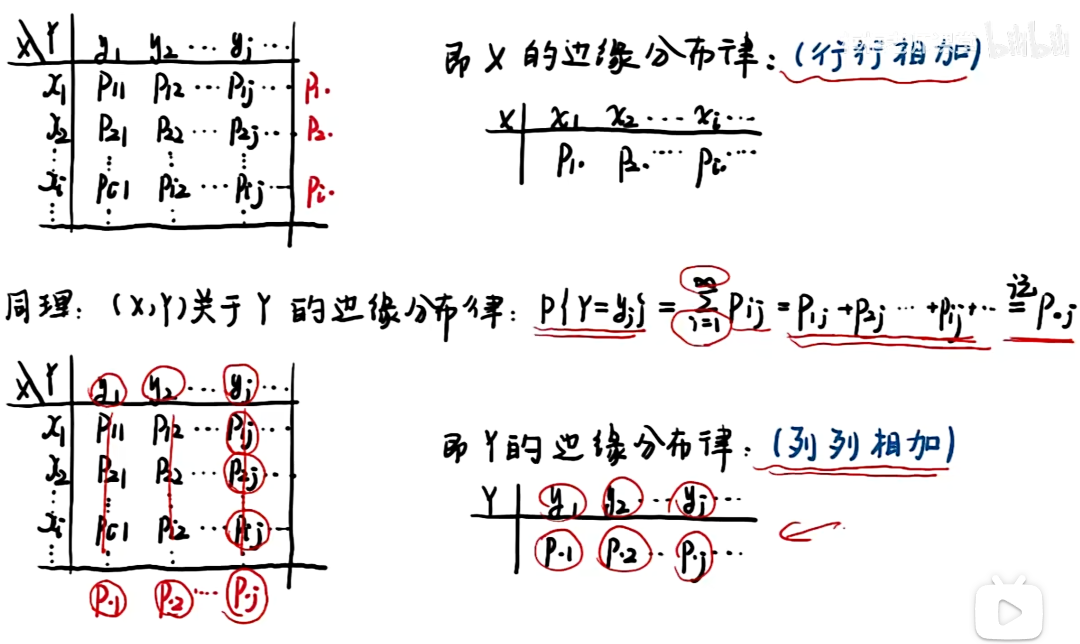
例题

知识点

例题


3.5 条件分布
知识点

例题

知识点

注:因为Y=y固定,在注①中y为常数,所以为一元函数;在注②中fY(y)也为常数可提取出来,后面的根据边缘密度函数公式可转换为fY(y);
例题


注:由于固定Y=y,则$-\sqrt{1-y2}和\sqrt{1-y2}$均为常数;


3.6 二维R.V的独立性
知识点

例题

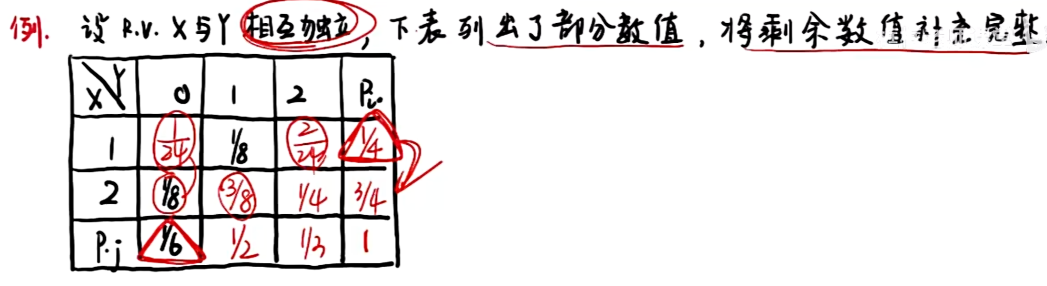



3.7 二维R.V函数的分布
例题
两个离散型R.V函数的分布

两个连续型R.V函数的分布





知识点
利用卷积公式求Z=X+Y的密度

例题


知识点

注:等价于——因为X,Y的最大值均小于Z,等价于两个变量分别都小于Z;
例题

第四讲 随机变量的数字特征
4.1 数学期望
知识点

例题
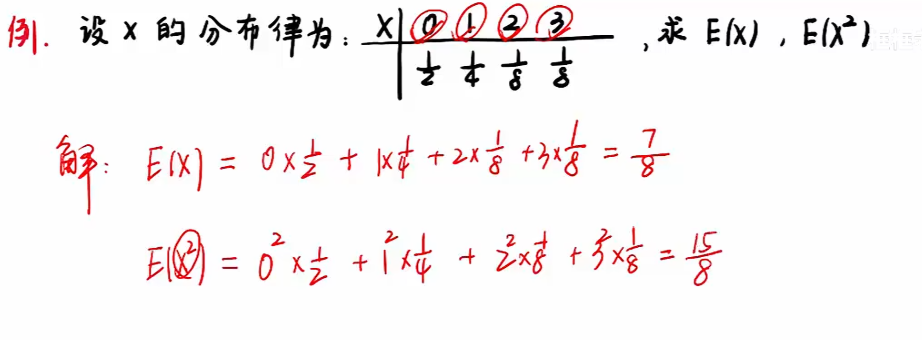

知识点

例题

连续型随机变量的数学期望
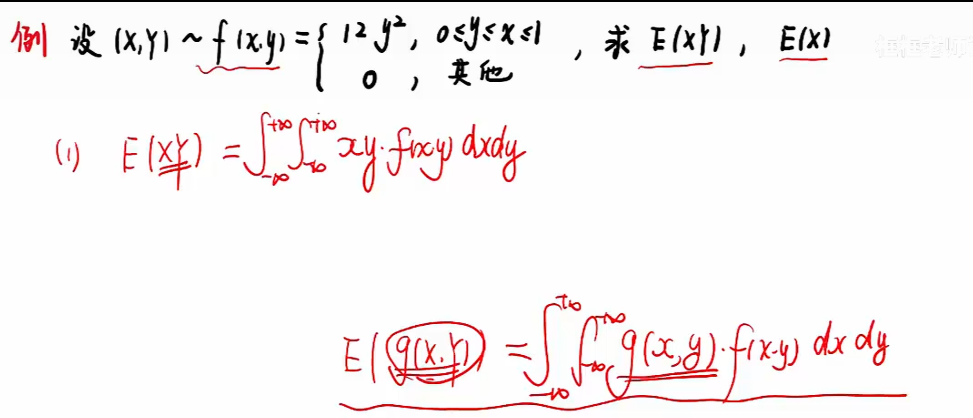

知识点

4.2 方差
知识点

例题
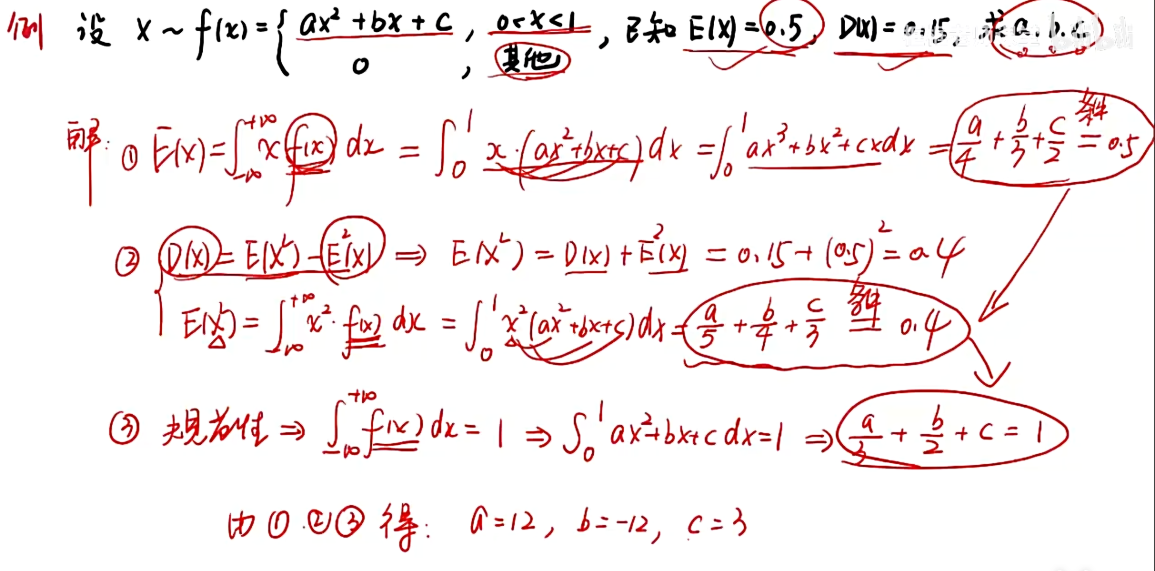
知识点
方差的性质

注:第4点,方差为0,说明随机变量等于它的数学期望是一个必然事件;
例题

4.3 常见分布的期望与方差
知识点


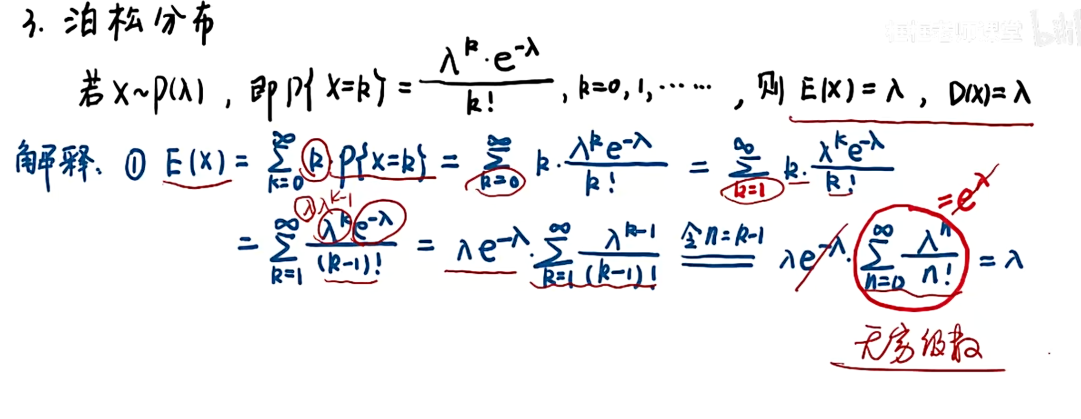
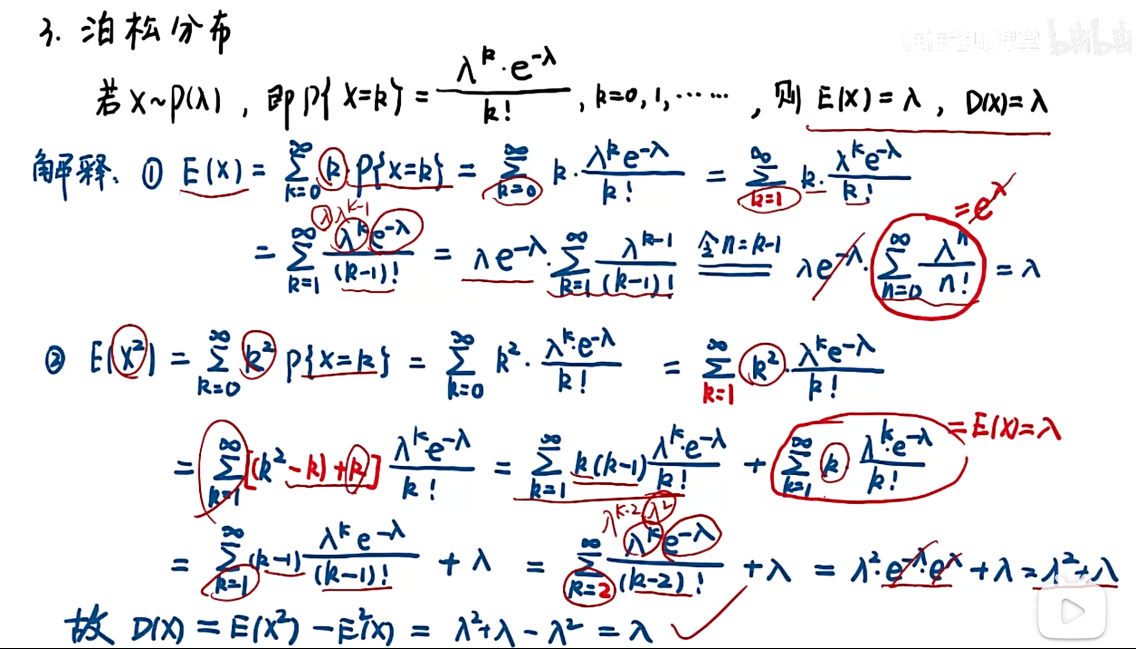
注:由于0^2 = 0 ,0乘以任何数都等于0,则将k=0改为k=1;
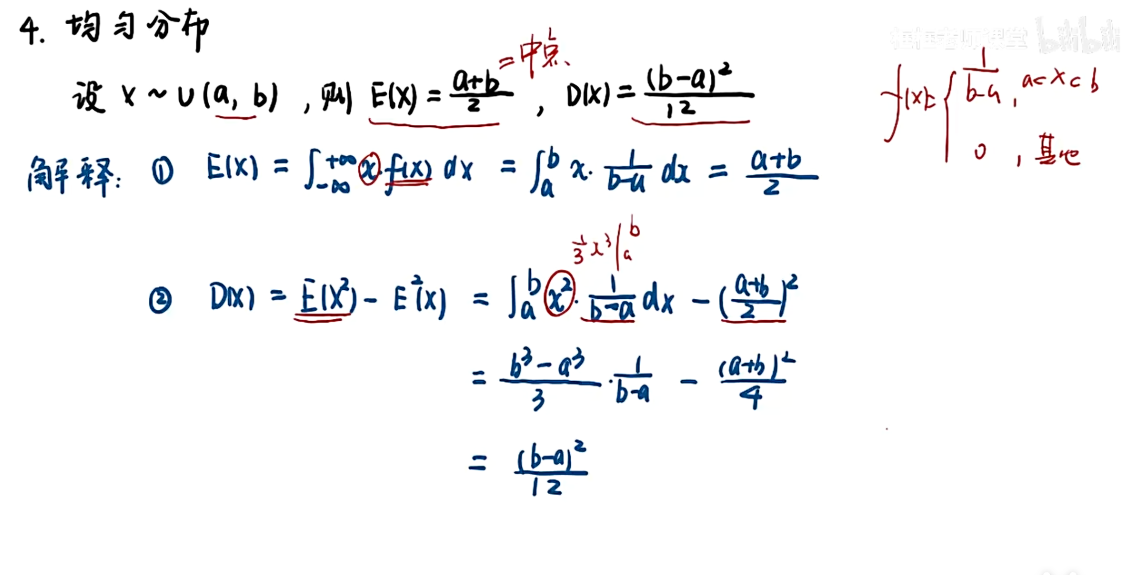

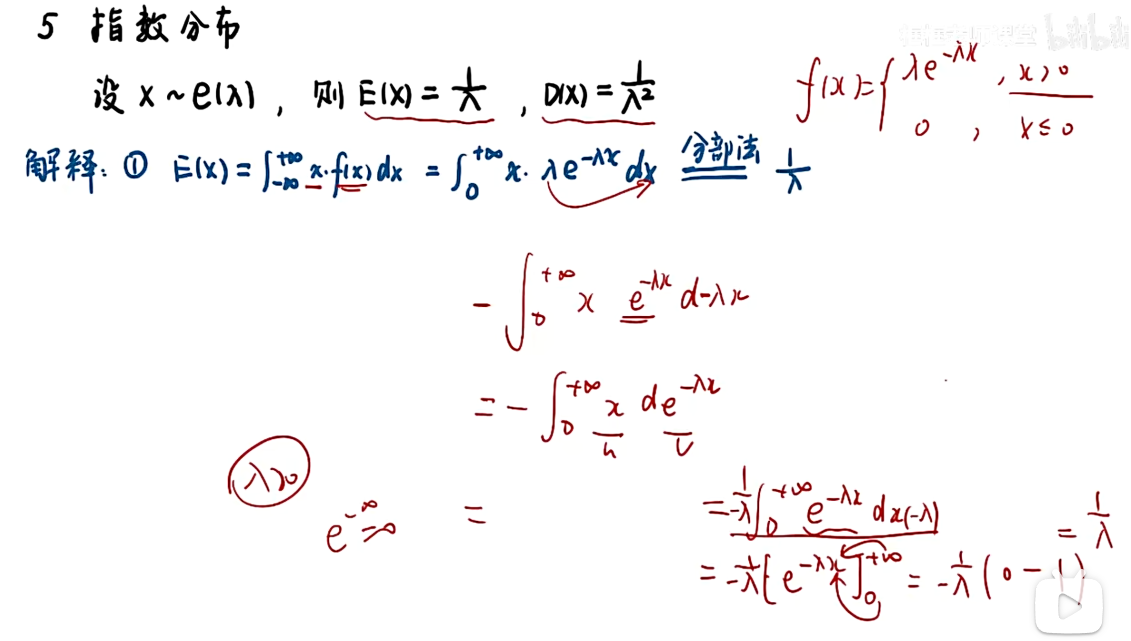


注:第二项是奇函数,积分后等于0;
例题


4.4 协方差与相关系数
知识点
协方差
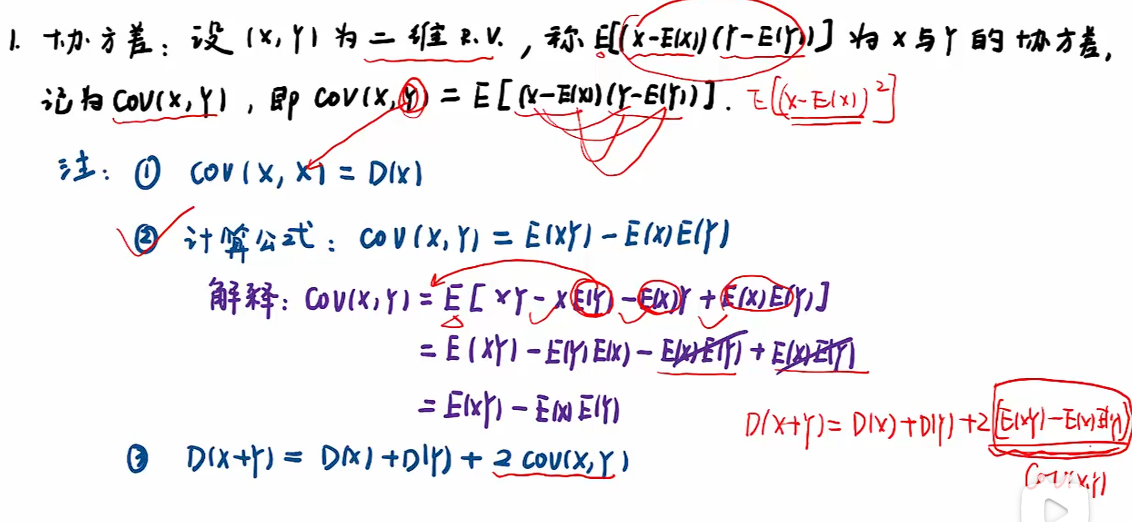

相关系数

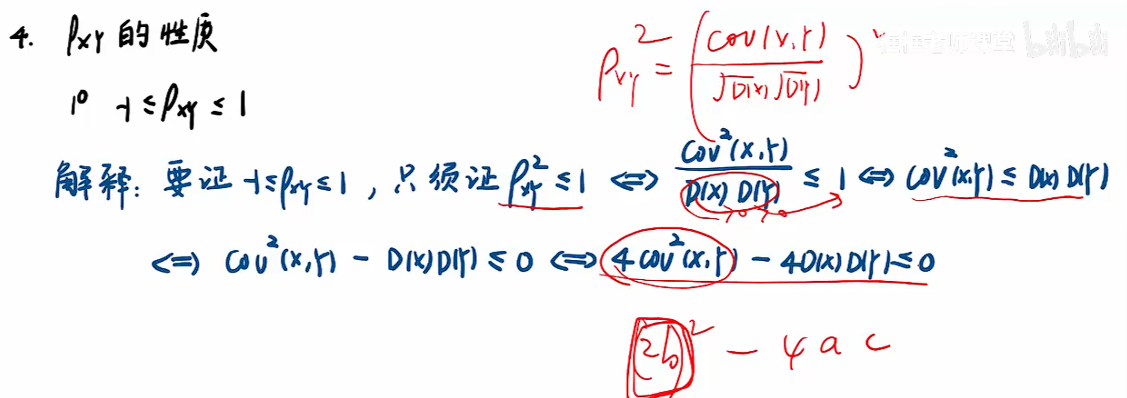
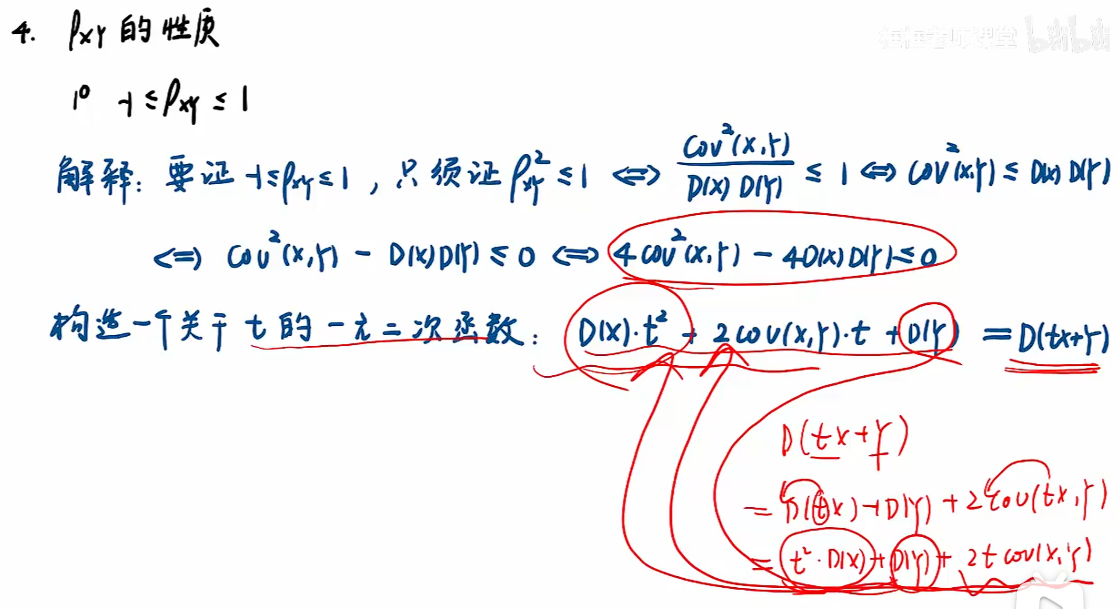

注:方差肯定大于等于0,因此关于t的一元二次函数也大于等于0;
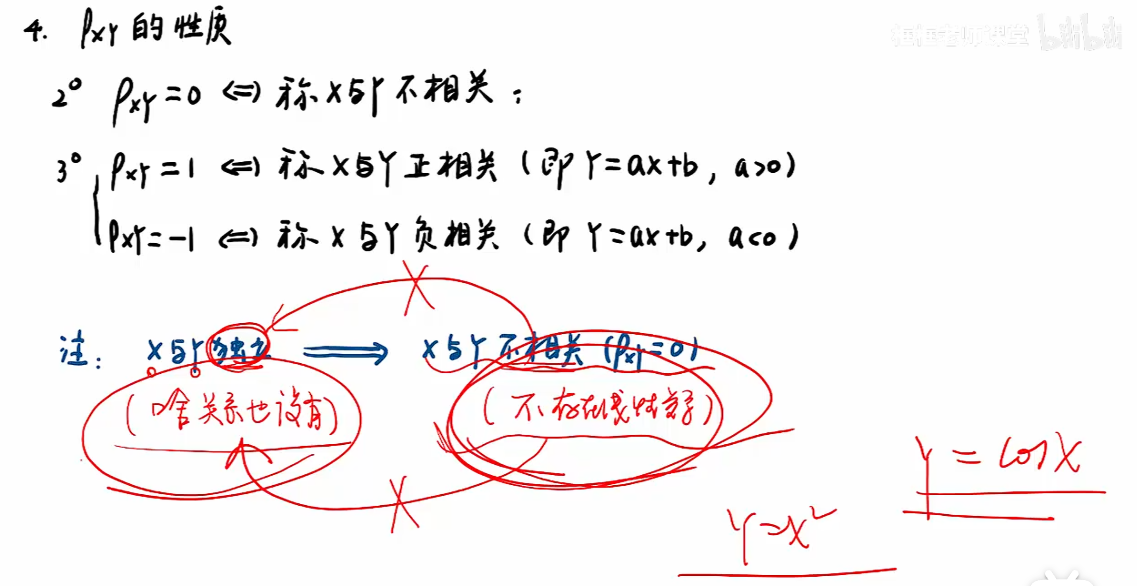
例题





第五讲 大数定律和中心极限定理
5.1 大数定律
知识点
切比雪夫不等式
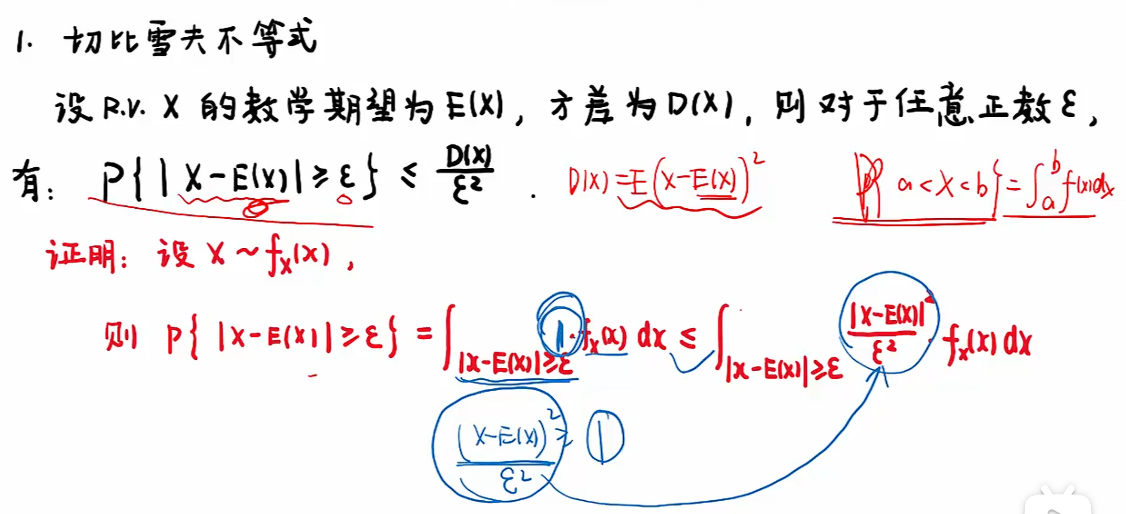

注:此处证明用了两次“放大”;

例题
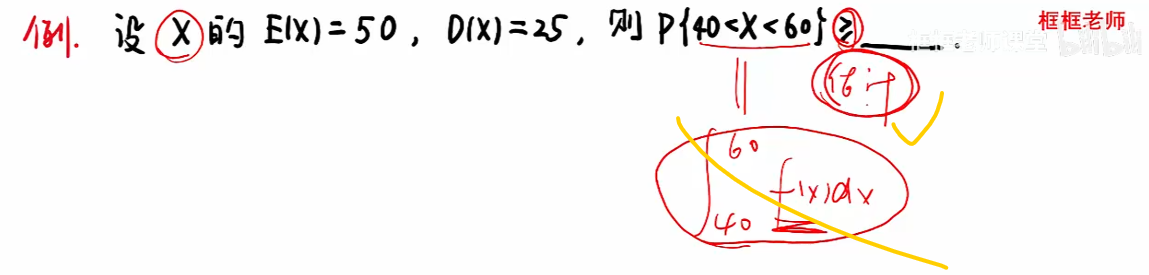

注:切比雪夫不等式只能估计,不像密度函数可以求出来具体等于多少;

知识点
切比雪夫大数定律

伯努利大数定律

辛钦大数定律

注:辛钦大数定律的条件:期望存在,但方差不一定存在
5.2 中心极限定理
知识点


注:当n趋于∞时,“近似”可以换为“精确”;

例题


注:涉及到求和就可以考虑中心极限定理;
第六讲 样本与抽样分布
6.1 数理统计的基本概念
知识点




注:当n充分大时,经验分布函数 约等于 总体分布函数;

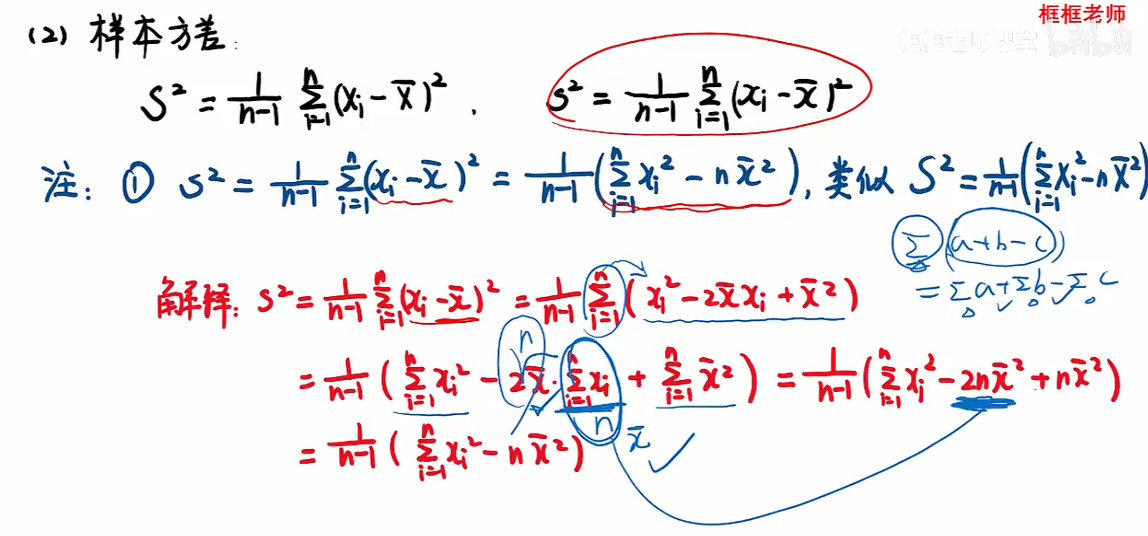 .
.

注:
- 第一个样本方差是修正方差,原本应除以n,修正后除以n-1,因为性质会更佳;
- x拔是常数;
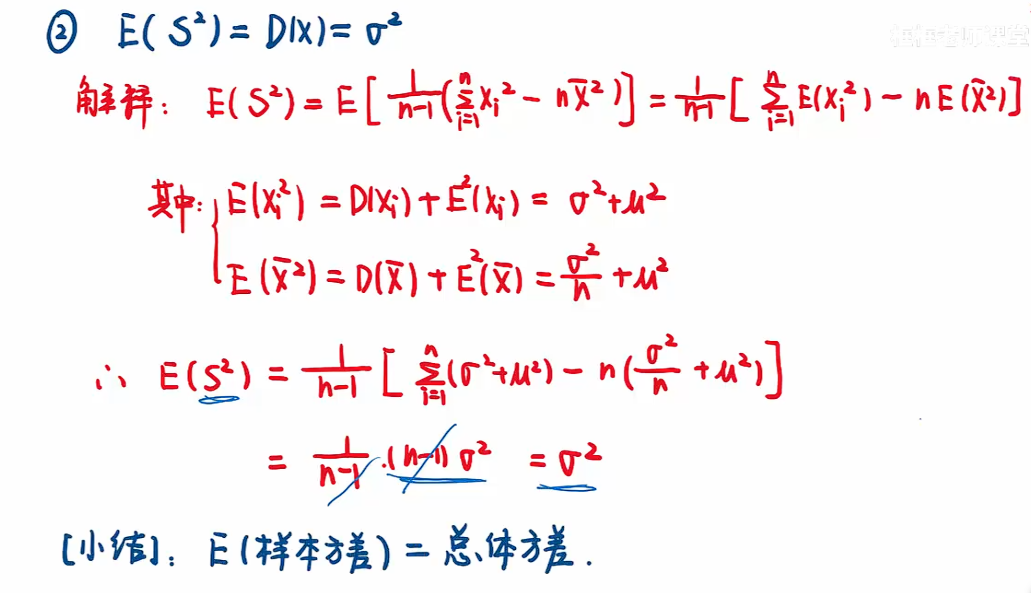

例题


6.2 抽样分布
知识点
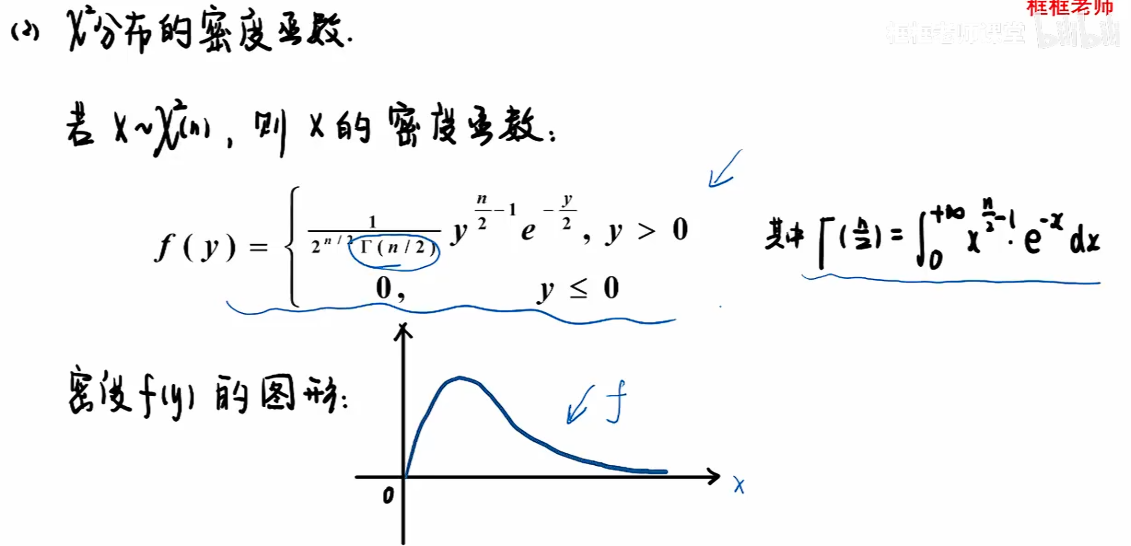
卡方分布


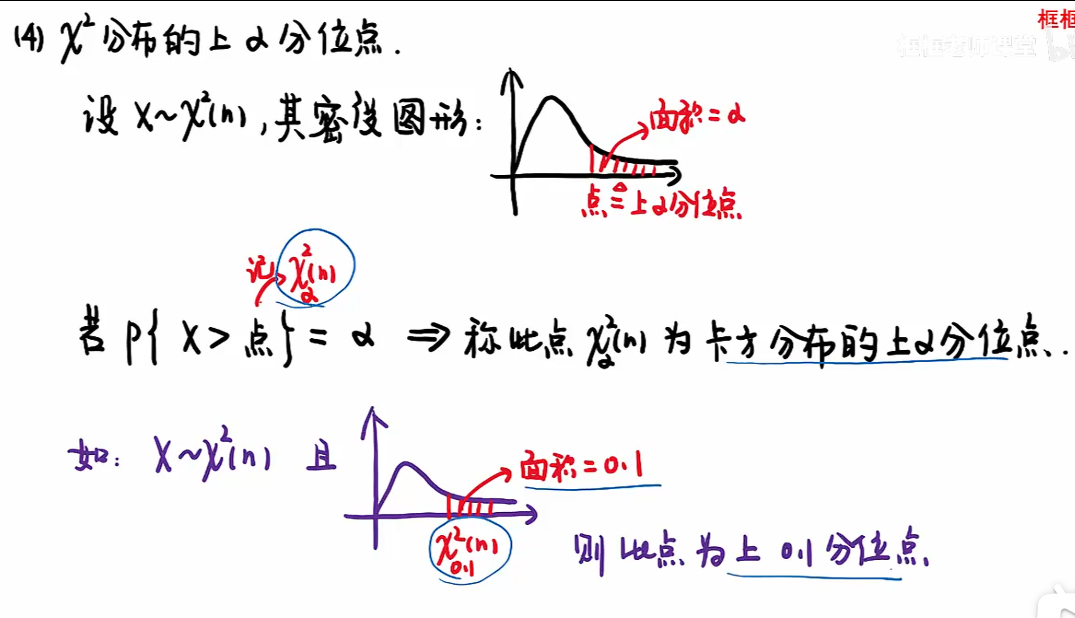
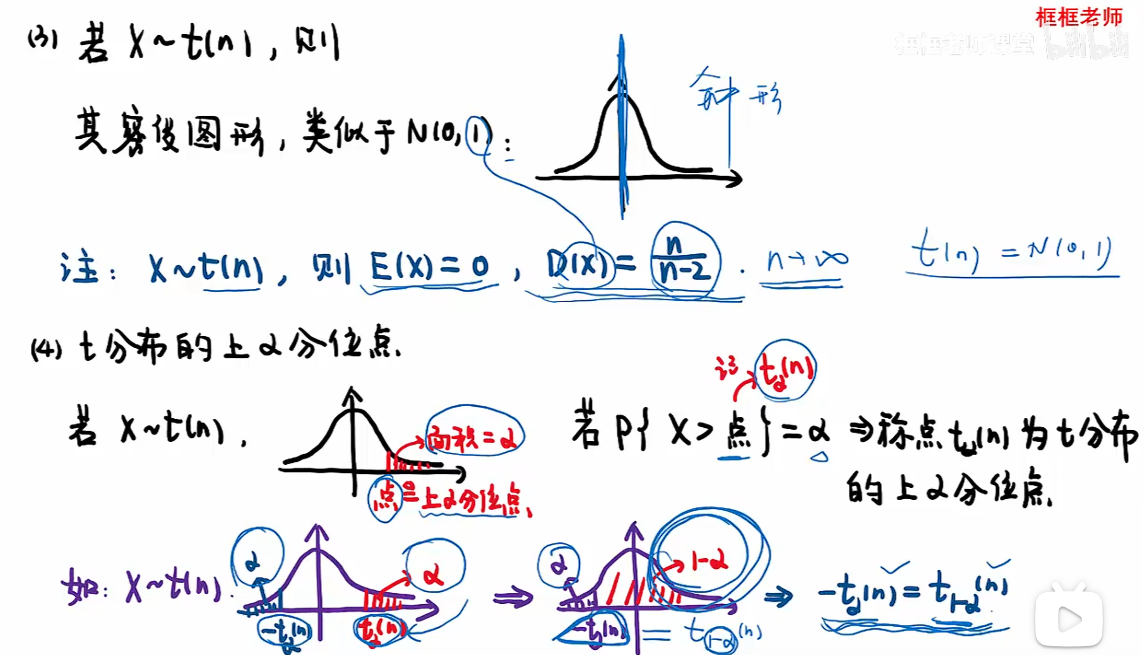
t分布

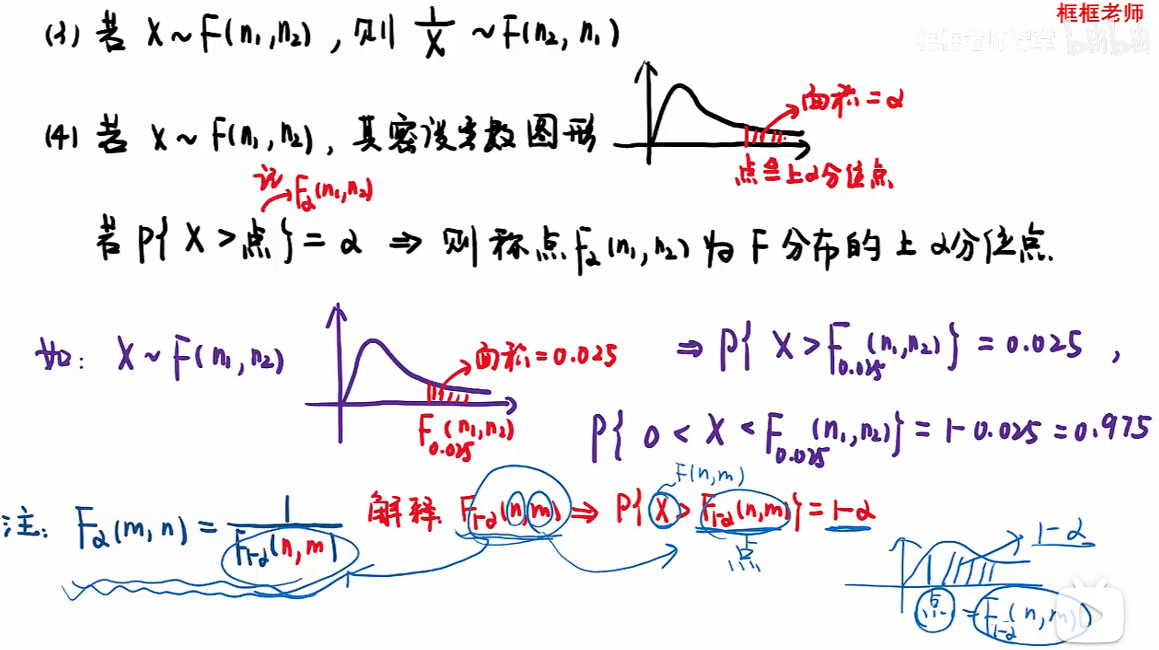
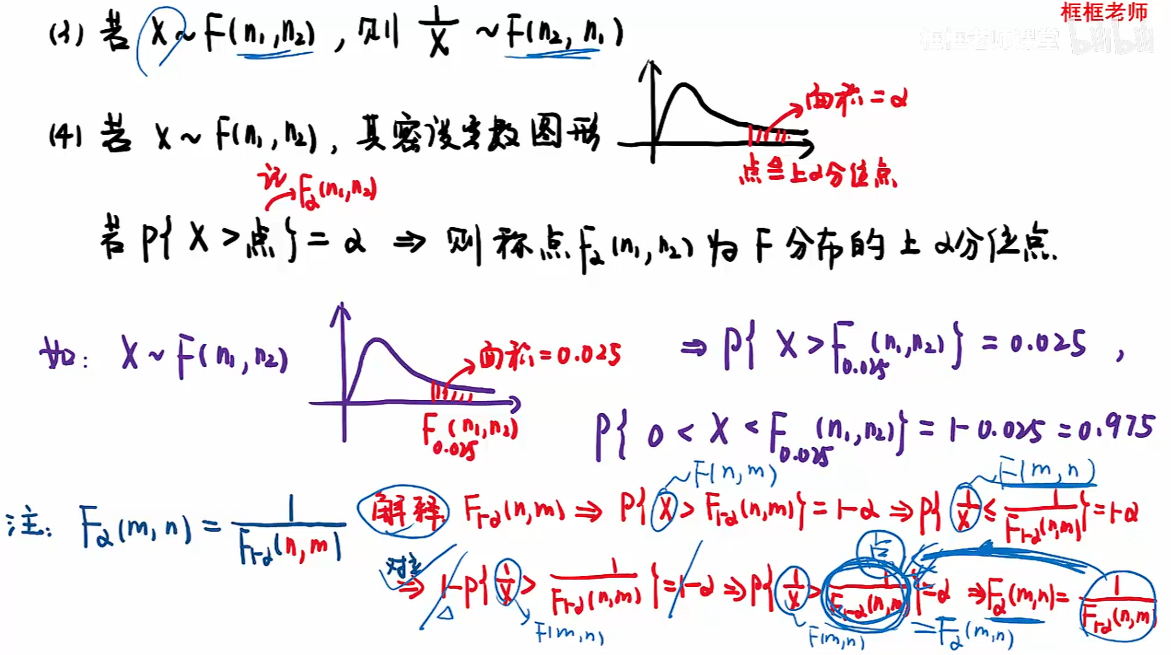
F分布

常见统计分布中 “n” 的含义对照表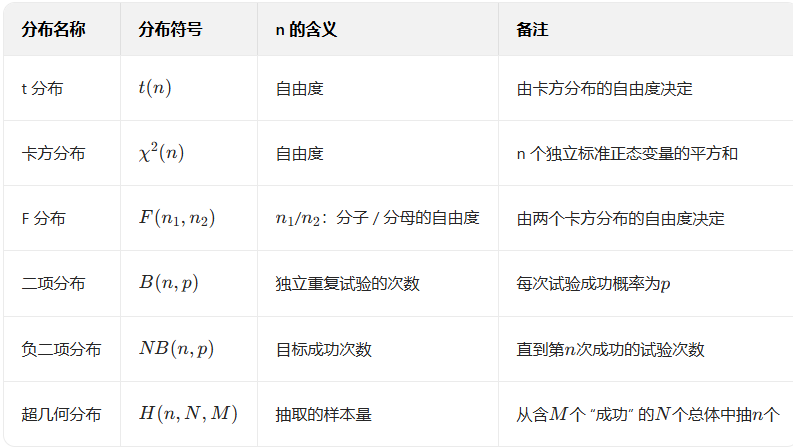
例题
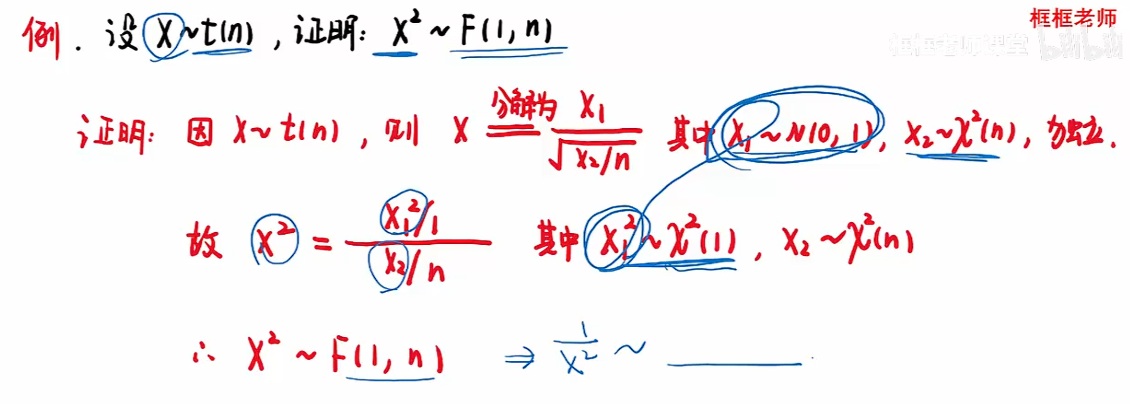
知识点
正态总体的样本均值与样本方差的分布

注:“理解①中”只要在独立的条件下,正态+正态还是正态,正态除以一个常数n也是正态;
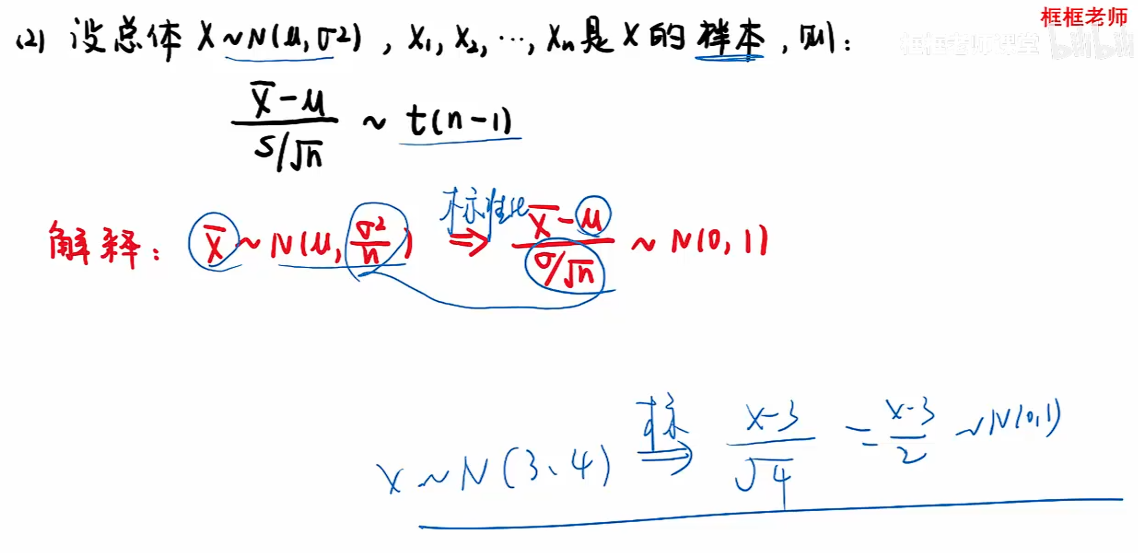

注:分子可得到一个标准正态,分母可得到一个卡方;并且分子分母相互独立;因此一个分子除以根号卡分,且根号里要除自由度n-1,就是t分布;
例题


知识点
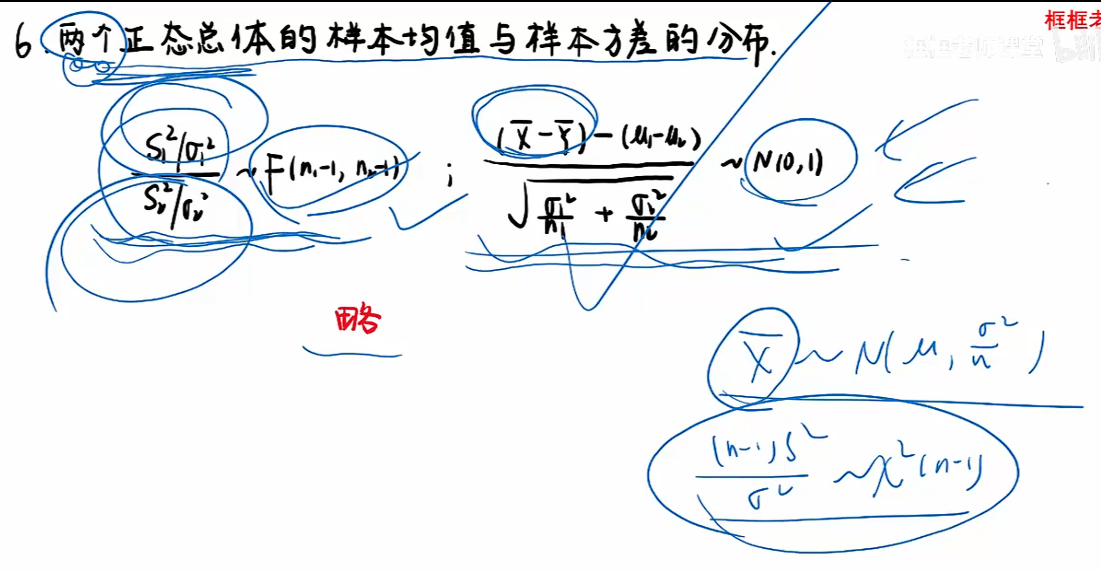
第七讲 参数估计
7.1 点估计
知识点
点估计

注:令总体的期望等于样本的均值
矩估计

注:总体矩E(x)右上角的“1”代表x的一次方;
例题


知识点
最大似然估计


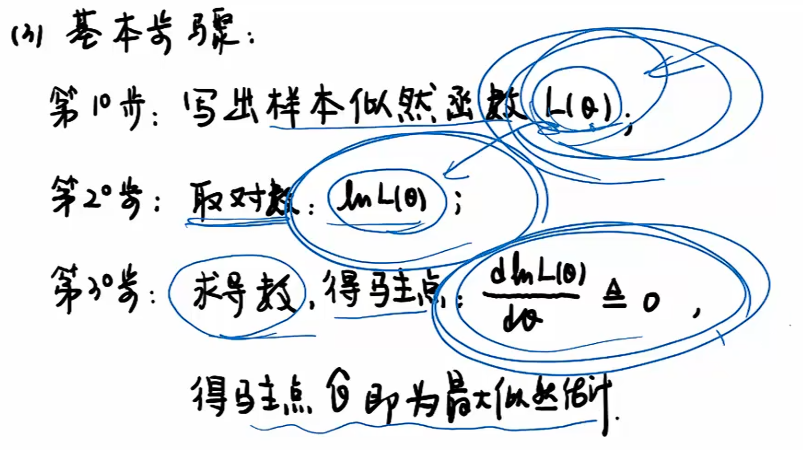
例题

注:X服从泊松分布,其是离散型的;

注:x1,x2···要求均大于0;
7.2 估计量的评选标准
知识点
无偏性(重点)

例题


注:由于x1,x2,···xi,xi+1是独立且同分布,因此其期望方差均相同,则平方的期望也相同;
知识点
有效性

例题

知识点
一致性
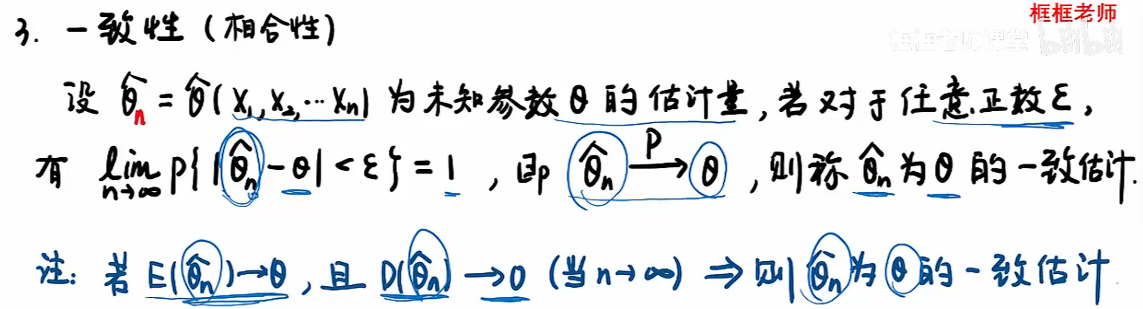
例题
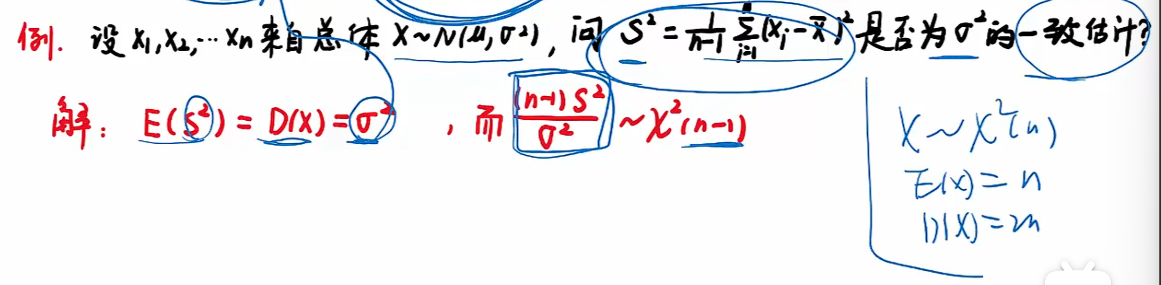
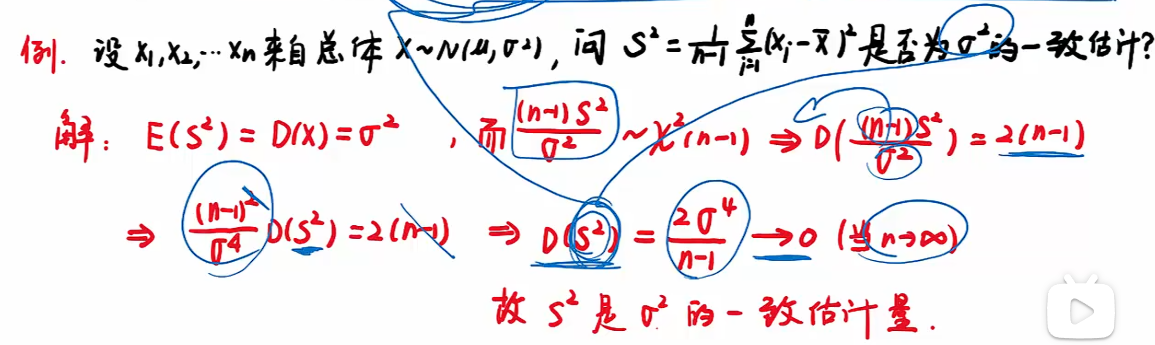
注:
- 第一步先看是否无偏;(样本方差的期望等于总体方差),因此由第一步得其是无偏的;
- 第二个公式,构建卡方分布,利用卡分分布性质,判断方差是否趋于0;
7.3 区间估计
知识点
置信区间

例题


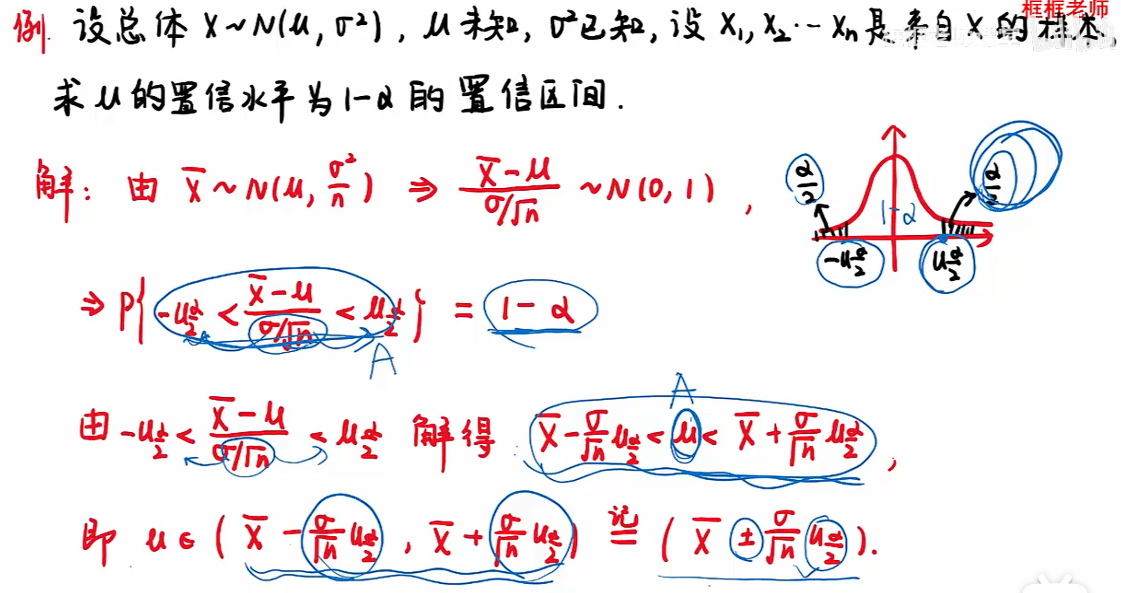
注:
思路——构造一个含有μ的函数;
第一步——样本均值也服从正态分布,将其标准化;
第二步——求出函数的范围(a,b),进而通过恒等变形求出μ的范围;
总结

注:此处的枢轴量指的就是J;
分情况:
情况一:

注:服从正态分布;
例题

情况二:


注:服从t分布;
例题:

注:S值题已告知,若未告知,则通过红色式子算;

情况三:
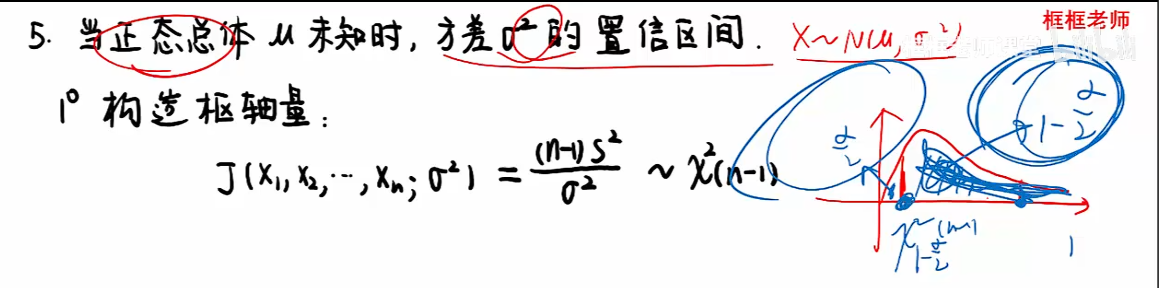

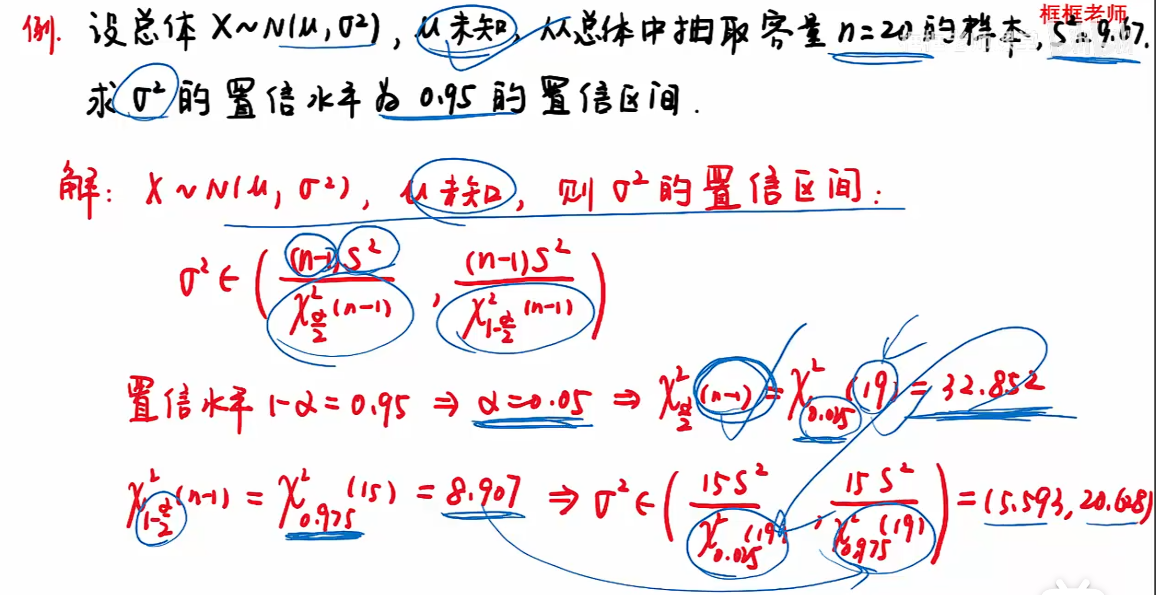
情况四:
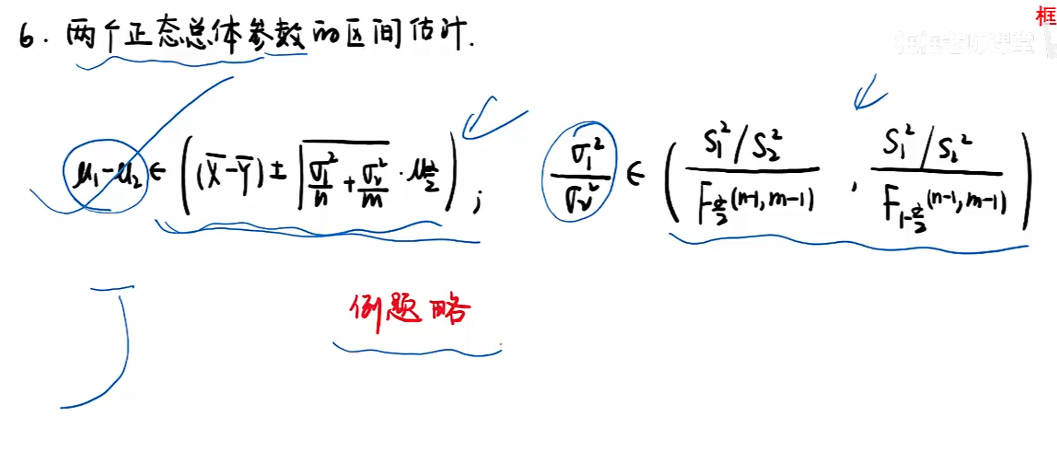
第八讲 假设检验
8.1 题型一
检查均值μ
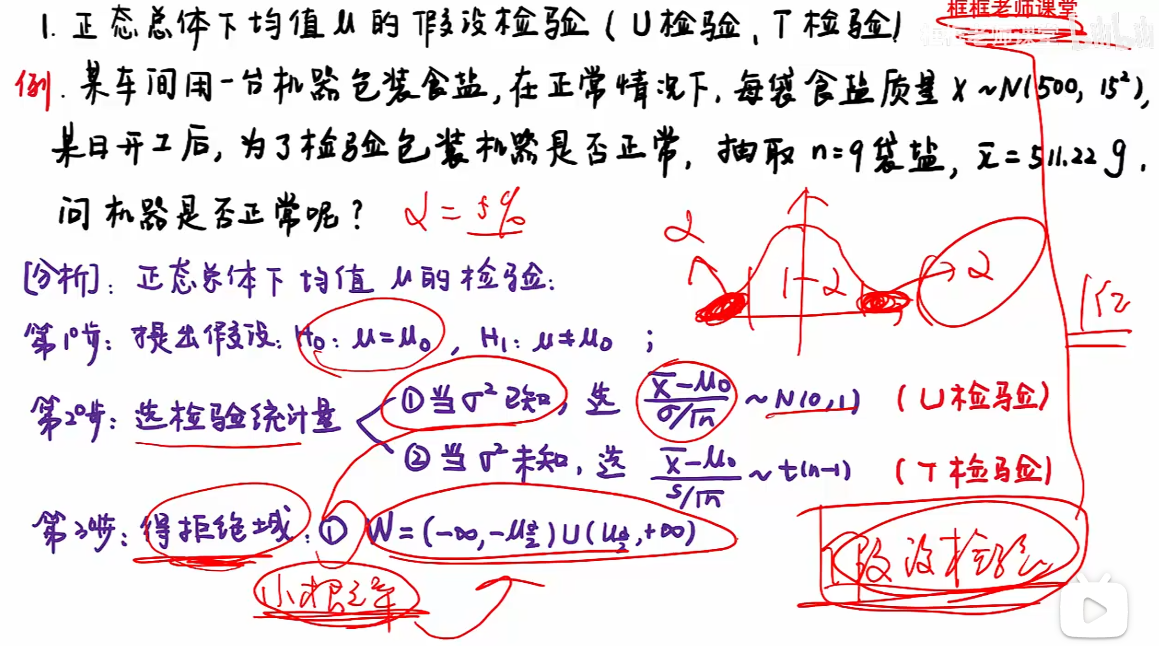
注:α指显著性水平;拒绝域指的是小概率事件对应的区间,即α概率构造的区间;.
假设检验:小概率事件在一次实验中基本不可能发生,如果发生,就要拒绝;
比如老师说他中了一个亿彩票,你本能就会不相信这个小概率事件;

注:若小概率事件落在拒绝域W,则拒绝H0,反之,接受H0;


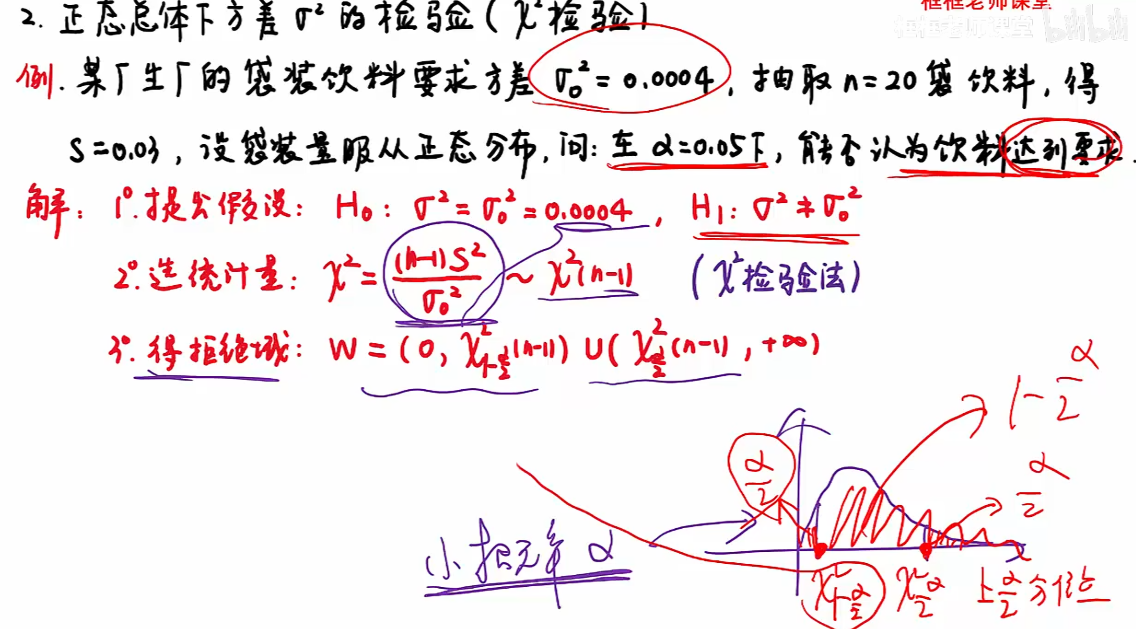
8.2 题型二
检查方差
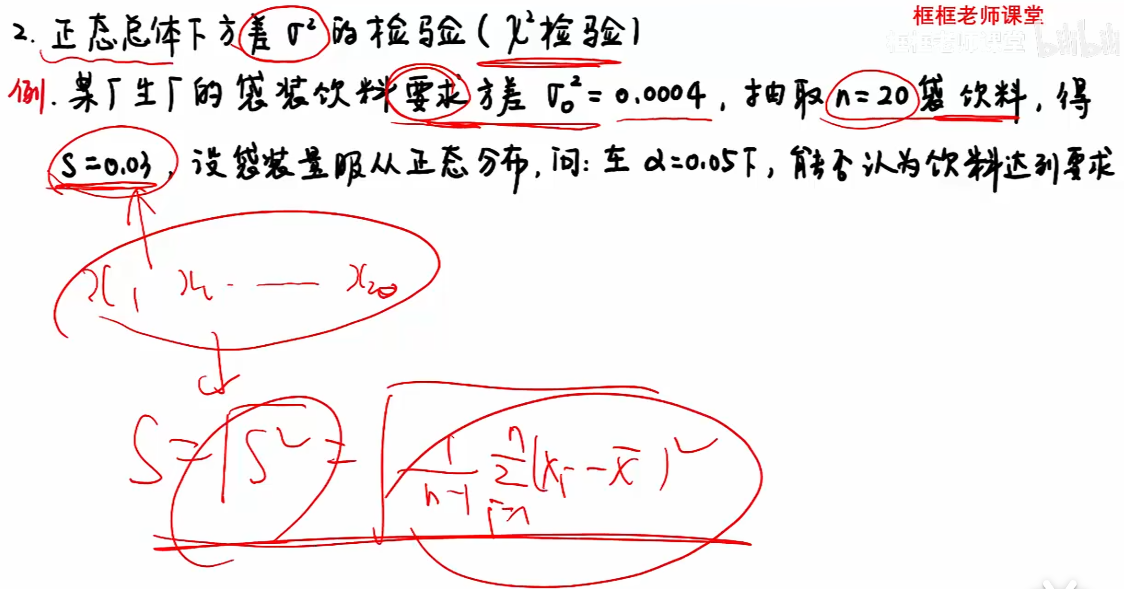
注:若题未告知S,则按上图中红色公式计算;




 浙公网安备 33010602011771号
浙公网安备 33010602011771号