Logistic回归

1 基本表述

    当\(Y\)是离散变量，\(X=(X_1,X_2,...,X_n)\)包含离散变量或连续变量，或两者都有时，可以用逻辑回归来学习函数\(f:X \to Y\)。逻辑回归先假设出了条件分布\(P(Y|X)\)的参数形式，然后直接用训练数据估计出其参数。当\(Y\)是布尔型变量（只包含两个类别）时，\(P(Y|X)\)的参数形式表示如下：

\[P(Y=1|X)=\frac 1 {1+\exp({\omega_0+\Sigma_{i=1}^n \omega_i X_i})}\\ \]

\[P(Y=0|X)=\frac {\exp(\omega_0 + \Sigma_{i=1}^n \omega_i X_i)} {1+\exp(\omega_0+\Sigma_{i=1}^n \omega_i X_i)} \]

    两个概率表达式的和为1。

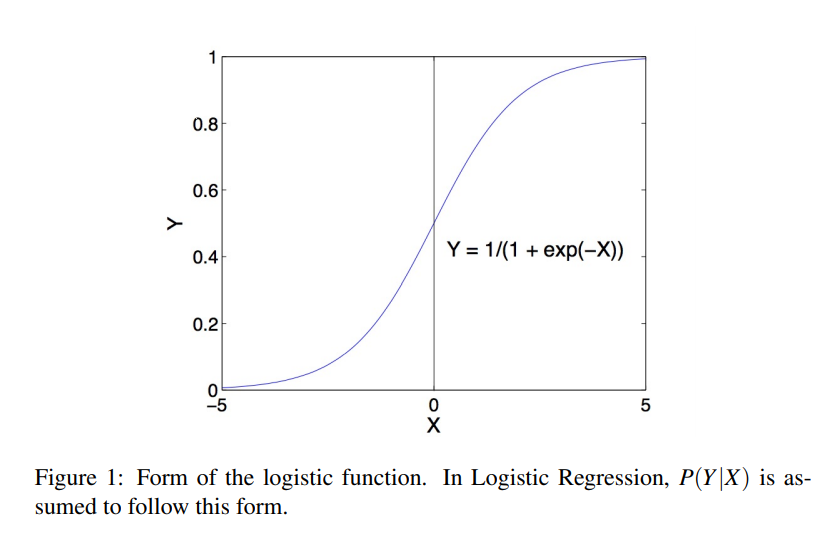
    这种形式的\(P(Y|X)\)使得分类过程只依赖于一种简洁的线性表达式。对于给定的\(X\)，我们通常去寻找使得\(P(Y=y_k|X)\)达到最大的\(y_k\)，将其作为给定实例的类别。换句话说，就是如果满足：

\[1 \lt \frac {P(Y=0|X)}{P(Y=1|X)} \]

    则令新实例的类别\(Y=0\)。上述条件可变换成：

\[1< \exp({\omega_0 + \Sigma_{i=1}^n \omega_iX_i}) \]

    两边取自然对数可得出将新实例的类别判定为0的线性分类规则：

\[0<\omega_0 + \Sigma_{i=1}^n \omega_iX_i \]

    否则将新实例的类别判定为1。

    Logistic回归所使用的\(P(Y|X)\)的参数形式正是高斯朴素贝叶斯分类器的假设所隐含的形式。因此，我们可以把Logistic回归看作是一种与GNB密切相关的替代方法，尽管在许多情况下，二者会产生不同的结果。

2 Gaussian Naive Bayes Classifier的\(P(Y|X)\)的表达式

    本节主要推导了高斯朴素贝叶斯（GNB）分类器的假设所产生的\(P(Y | X)\)形式，表明它正是Logistic回归所使用的\(P(Y | X)\)形式。特别地，考虑基于以下建模假设的GNB：

• \(Y\)是布尔型变量，由二项分布生成，参数\(\pi=P(Y=1)\)
• \(X=(X_1,X_2,...,X_n)\)，每个\(X_i\)均为连续型随机变量
• 对每个\(X_i\)来说，\(P(X_i|Y=y_k)\)是一个高斯分布\(N(\mu_{ik},\sigma_i)\)（注意到标准差\(\sigma_i\)只与特征有关，与类别无关）
• 对于所有的\(i,j\ne i\)，在给定\(Y\)的情况下，\(X_i\)和\(X_j\)条件独立

    我们现在从这组GNB假设中推导出\(P(Y | X)\)的参数形式。一般来说，Bayes规则允许我们写作如下形式：

\[P(Y=1|X)=\frac {P(Y=1)P(X|Y=1)}{P(Y=1)P(X|Y=1)+P(Y=0)P(X|Y=0)} \]

    通过分子分母同时除以分子得：

\[P(Y=1|X)=\frac 1 {1+ \frac {P(Y=0)P(X|Y=0)}{P(Y=1)P(X|Y=1)}} \]

    等价于：

\[P(Y=1|X)=\frac 1 {1+ \exp(ln\frac {P(Y=0)P(X|Y=0)}{P(Y=1)P(X|Y=1)})} \]

    由于特征条件独立假设，可将上式写成：

\[\begin{aligned} P(Y=1|X)&=\frac 1 {1+ \exp(ln\frac {P(Y=0)}{P(Y=1)} + \Sigma_i ln \frac {P(X_i|Y=0)} {P(X_i|Y=1)})}\\ &= \frac 1 {1+ \exp(ln\frac {1-\pi}{\pi} + \Sigma_i ln \frac {P(X_i|Y=0)} {P(X_i|Y=1)})} \end{aligned} \]

    现在考虑分母中累计和的表达式，在\(P(X_i|Y=y_k)\)为高斯分布的假定条件下，可将累计和表达式展开为：

\[\begin{aligned} \Sigma_i ln \frac {P(X_i|Y=0)}{P(X_i)Y=1} &=\Sigma_iln \frac {\frac 1 {\sqrt{2 \pi \sigma_i^2}} \exp(\frac {-(X_i-\mu_{i0})^2}{2\sigma_i^2})}{\frac 1 {\sqrt{2 \pi \sigma_i^2}} \exp(\frac {-(X_i-\mu_{i1})^2}{2\sigma_i^2})}\\ &=\Sigma_iln \exp(\frac{(X_i-\mu_{i1})^2-(X_i-\mu_{i0})^2}{2\sigma_i^2})\\ &=\Sigma_i(\frac{(X_i-\mu_{i1})^2-(X_i-\mu_{i0})^2}{2\sigma_i^2})\\ &=\Sigma_i(\frac{(X_i^2-2X_i\mu_{i1}+\mu_{i1}^2)-(X_i^2-2X_i\mu_{i0}+\mu_{i0}^2)}{2\sigma_i^2})\\ &=\Sigma_i(\frac{2X_i(\mu_{i0}-\mu_{i1})+\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2})\\ &=\Sigma_i(\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}X_i+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2}) \end{aligned} \]

    该表达式是特征变量\(X_i\)的线性加权和，将其重新代回\(P(Y=1|X)\)的表达式，有：

\[P(Y=1|X)=\frac 1 {1+ \exp(ln\frac {1-\pi}{\pi} + \Sigma_i(\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}X_i+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2}))} \]

    其等价于：

\[P(Y=1|X)=\frac 1 {1+ \exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} \]

    其中：

\[\omega_i=\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}\\ \omega_0=ln \frac{1-\pi}\pi + \Sigma_i \frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2} \]

    因此：

\[P(Y=0|X)=1-P(Y=1|X)=\frac {\exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} {1+ \exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} \]

3 逻辑回归的参数估计

    上一小节证明了在高斯朴素贝叶斯的假设下，其\(P(Y|X)\)正是逻辑回归中的\(P(Y|X)\)的形式，并且还给出了\(\omega_i\)的表达式。本节给出逻辑回归的参数估计更一般的方法。不直接使用高斯朴素贝叶斯假设下的\(P(Y|X)\)主要是因为：

• 逻辑回归所假设的\(P(Y|X)\)在很多问题环境中都适用，可能超出了GNB（高斯朴素贝叶斯）对应的问题。
• 在很多情况下，GNB的假设并不能完全满足，需要从数据中直接估计\(\omega_i\)，而不是依赖于GNB估计过程。

    训练Logistic回归的一个合理方法是选择使条件数据的似然最大化的参数值。条件数据似然是训练数据中以它们对应的X值为条件，观察到当前Y值的概率。选择满足以下条件的权重参数\(W\)：

\[W \leftarrow arg \max_{W} \prod_lP(Y^l|X^l,W) \]

    其中，\(W=(\omega_0,\omega_1,...,\omega_n)\)是需要估计的参数向量，\(Y^l\)表示第\(l\)个训练样本的\(Y\)的观测值，\(X^l\)表示第\(l\)个训练样本的\(X\)的观测值，\(\prod_lP(Y^l|X^l,W)\)即代表条件数据似然，这里将权重向量\(W\)列在条件里面，表示这个表达式是关于\(W\)的函数。

    等价地，可以写出其对数似然的表达式：

\[W \leftarrow arg \max_{W} \sum_l ln P(Y^l|X^l,W) \]

    其中的条件数据对数似然可以记为：

\[l(W)=\Sigma_l( Y^l lnP(Y^l=1|X^l,W)+(1-Y^l)lnP(Y^l=0|X^l,W)) \]

    其中，\(Y\)值只能为1或者0，对于给定的\(Y^l\)，累计和符号后面求和的两个表达式一个为0，一个非0 。

    为了和通常做法一致，此处调换变量\(P(Y=0|X)\)和\(P(Y=1|X)\)的表达式：

\[P(Y=0|X)=\frac 1 {1+ \exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} \]

\[P(Y=1|X)=\frac {\exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} {1+ \exp(\omega_0+\Sigma_{i=1}^n \omega_iX_i)} \]

    因此，对数条件似然的表达式可写为：

\[\begin{aligned} l(W) &=\sum_{l} Y^{l} \ln P\left(Y^{l}=1 \mid X^{l}, W\right)+\left(1-Y^{l}\right) \ln P\left(Y^{l}=0 \mid X^{l}, W\right) \\ &=\sum_{l} Y^{l} \ln \frac{P\left(Y^{l}=1 \mid X^{l}, W\right)}{P\left(Y^{l}=0 \mid X^{l}, W\right)}+\ln P\left(Y^{l}=0 \mid X^{l}, W\right) \\ &=\sum_{l} Y^{l}\left(w_{0}+\sum_{i}^{n} w_{i} X_{i}^{l}\right)-\ln \left(1+\exp \left(w_{0}+\sum_{i}^{n} w_{i} X_{i}^{l}\right)\right) \end{aligned} \]

    其中，\(X_i^l\)表示第\(l\)个训练样本的第\(i\)个特征\(X_i\)的观测值，注意到上标\(l\)与对数似然函数\(l(W)\)无关。

    然而，并不存在使\(l(W)\)最大的\(W\)的闭式解（显示表达式），一种常见的做法是使用梯度上升，主要考虑偏导数的梯度向量。向量梯度第\(i\)个分量的形式为：

\[\frac{\partial l(W)}{\partial \omega_i} =\sum_l X_i^l(Y^l-\hat P(Y^l=1|X^l,W)) \]

    其中，\(\hat p(Y^l|X^l,W)\)表示逻辑回归的预测值；为了考虑权重\(\omega_0\)，可以设一个定值变量\(X_0=1\)，适用于所有\(l\)。这个偏导数有一个直观的解释：括号里的表达式为预测误差。注意到当\(Y^l\)为1时我们希望\(\hat p(Y^l=1|X^l,W)\)为1，反之亦然，这个误差表达式乘了一个\(X_i^l\)，这就解释了预测时\(\omega_iX_I^l\)的重要性。

    给出了每个\(w_i\)的偏导表达式，我们可以使用标准梯度上升来优化权重\(W\)。从初始权重为0开始，我们沿着梯度的方向反复更新权重，每次迭代时根据下列公式：

\[\omega_i \leftarrow \omega_i + \eta \sum_l X_i^l(Y^l-\hat P(Y^l=1|X^l,W)) \]

    这里\(\eta\)是一个值很小的常量（如0.01），它决定了迭代的步长。由于条件对数似然函数\(l(W)\)是凹函数，因此梯度上升过程会收敛到一个全局最大值。梯度上升法已经被详尽讨论，通常使用共轭梯度上升法，收敛速度更快。

4 逻辑回归中的正则化

    逻辑回归中同样可能出现过拟合的问题，特别是当特征变量特别多且训练数据较为稀少的时候。一种降低过拟合的方式是正则化，即新建一种使较大值的\(W\)将受到更多惩罚的带惩罚项修正过的的对数似然函数：

\[W \leftarrow arg \max_W \sum_l lnP(Y^l|X^l,W)-\frac {\lambda} 2 ||W||^2 \]

    其中，加了一个与权重向量\(W\)的范数成正比的惩罚项，这里的\(\lambda\)是一个正的常数，它决定了该惩罚项的惩罚强度。

    加入惩罚项后目标函数发生了变化。在\(P(W)\)的先验分布时均值为0，方差与\(1/\lambda\)有关的正态分布的假设条件下，最大化目标函数\(l(W)\)相当于计算参数\(W\)的最大后验估计（MAP）。通常情况下，参数\(W\)的MAP估计涉及到下述目标的优化问题：

\[\sum_llnP(Y^l|X^l,W)+lnP(W) \]

    如果\(P(W)\)是一个0均值的正态分布，\(lnP(W)\)将产生一个与\(||W||^2\)成比例的式子。

    给定带惩罚项的对数似然函数后，可以类比不带惩罚项的对数似然函数求偏导过程，推导出其梯度上升规则：

\[\frac{\partial l(W)}{\partial \omega_i} =\sum_l X_i^l(Y^l-\hat P(Y^l=1|X^l,W))-\lambda \omega_i \]

    可以得出修改后的梯度上升规则：

\[\omega_i \leftarrow \omega_i + \eta \sum_l X_i^l(Y^l-\hat P(Y^l=1|X^l,W))-\eta\lambda\omega_i \]

    在我们对特定\(\omega_i\)的可能值有先验知识的情况下，可以通过使用非零均值的\(W\)上的正态先验信息来推导类似的惩罚项。

5 多分类变量的逻辑回归

    上面讨论了当\(Y\)为布尔型变量时如何用逻辑回归来学习\(P(Y|X)\)，更一般的情形是\(Y\)具有多个类别\({y_1,y_2,...,y_K}\)，其条件概率可表示为：

\[P\left(Y=y_{k} \mid X\right)=\frac{\exp \left(w_{k 0}+\sum_{i=1}^{n} w_{k i} X_{i}\right)}{1+\sum_{j=1}^{K-1} \exp \left(w_{j 0}+\sum_{i=1}^{n} w_{j i} X_{i}\right)} \]

    当\(Y=y_k\)时，

\[P\left(Y=y_{K} \mid X\right)=\frac 1 {1+\sum_{j=1}^{K-1} \exp \left(w_{j 0}+\sum_{i=1}^{n} w_{j i} X_{i}\right)} \]

    这里的\(w_{ji}\)表示与第\(j\)个类别\(Y=y_j\)，第\(i\)个特征\(X_i\)相关的权重。当\(K=2\)时，即为二分类的条件概率表达式。同时各类别的条件概率的表达式和为1。

    上述表达式与二分类的表达式最大的不同是\(Y\)有\(K\)个不同的值，需要构建\(K-1\)个不同的线性表达式来刻画\(Y\)的不同值的分布。对于\(Y\)的第\(K\)个值，即其最后一个值来说，其概率是1减去前\(K-1\)个值的概率和。

    此时，正则化的梯度上升规则为：

\[w_{ji} \leftarrow w_{ji}+\eta \sum_l X_i^l(\delta(Y^l=y_j)-\hat P(Y^l=y_j|X^l,W))-\eta\lambda w_{ji} \]

    其中\(\delta(Y^l=y_j)=1\)表示第\(l\)个训练样本的类别变量\(Y^l\)的值为\(y_j\)，即该实例属于第\(j\)个类，否则\(\delta(Y^l=y_j)=0\)。括号里的量表示真实概率与估计概率的差异，当模型估计值完全匹配上观测值时，该差异为0。

6 朴素贝叶斯分类器和Logistic回归的关系

概括地说，逻辑回归直接估计了\(P(Y|X)\)的参数，而朴素贝叶斯直接估计的是\(P(Y)\)和\(P(Y|X)\)。我们通常将前者称为有判别力的分类器（discriminative classfier），后者称为有生产力的分类器（generative classifier）。

上述第2小节展示了在一种高斯朴素贝叶斯分类器的假设条件下，最后得出的\(P(Y|X)\)就是逻辑回归使用的参数形式的\(P(Y|X)\)，并且逻辑回归中的参数\(w_i\)可以用高斯朴素贝叶斯的参数来表示。事实上，如果GNB的假设条件成立，随着训练样本数的无限增长，GNB和Logistic回归会渐近地收敛到相同的分类器。

但这两种算法在某些方面也有差异：

• 当GNB建模假设不成立时，Logistic回归和GNB通常学习不同的分类器函数。在这种情况下，Logistic回归的渐近（训练样本数接近无穷大）分类精度往往优于GNB的渐近精度。虽然Logistic回归与朴素贝叶斯假设一致，即输入特征\(X_i\)在给定\(Y\)的条件下是独立的，但它并不像naivebayes那样严格地依赖于这个假设。对于不符合这一假设的数据，Logistic回归的条件似然最大化算法将调整其参数，使其与数据的拟合（条件似然）最大化，即使得到的参数与朴素贝叶斯参数估计不一致。
• GNB和Logistic回归以不同的速率收敛于其渐近精度。在\(log\) n阶例子中（ in order log n examples），GNB参数估计收敛于其渐近值，其中n是\(X\)的维数。相比之下，Logistic回归参数估计收敛得更慢，需要n阶例子（ requiring order n examples. ）。在多个数据集中，当训练样本较多时，Logistic回归的表现优于GNB，而在训练数据较少时，GNB的表现优于Logistic回归。

7 总结

• 我们可以用贝叶斯规则作为设计学习算法（即函数逼近器）的基础。具体如下：假设我们希望学习某个目标函数\(f:X\to Y\)，或者等价地，\(P(Y|X)\)，我们利用训练数据来获得\(P(X|Y)\)和\(P(Y)\)的估计。然后使用这些估计的概率分布，再加上Bayes规则，可以对新的\(X\)示例进行分类。这种类型的分类器称为生成分类器，因为我们可以将分布\(P(X|Y)\)视为如何根据目标属性\(Y\)生成随机实例\(X\)的规则描述。
• 直接学习Bayes分类器需要极大数量（超过\(|X|\)，\(X\)是实例空间）的训练实例，除非对\(P(Y|X)\)做出某种形式的预先假设。NB分类器假设所有的特征变量\(X_i\)在给定\(Y\)的条件下是独立的。这个假设极大地减少了学习分类器时必须估计的参数数量。NB是一种广泛应用的学习算法，适用于离散型和连续型的\(X\)。
• 当\(X\)是离散值属性向量时，NB学习算法可以看作线性分类器，即每个朴素贝叶斯分类器对应于\(X\)中的一个超平面决策曲面。如果假设每个特征\(X_i\)的方差与类别\(y_k\)无关(\(\sigma_{ik}=\sigma_i\)），那么上述描述同样适用于高斯朴素Bayes分类器。
• Logistic回归是一种函数逼近算法，不同于NB，它使用训练数据直接估计\(P(Y|X)\)。在这个意义上，逻辑回归通常被称为判别分类器，因为它可以将分布\(P(Y|X)\)看作是对给定实例\(X\)的目标值\(Y\)的直接判别。
• Logistic回归是\(X\)上的线性分类器。在朴素贝叶斯假设成立的前提下，Logistic回归和Gaussian朴素贝叶斯提出的线性分类器在训练样本数接近无穷大的情况下，在极限上是相同的。然而，如果这些假设不成立，朴素的Bayes偏差将导致它在一定程度上比Logistic回归更不准确。换句话说，NB是一种比逻辑回归有更大偏差但方差更低的学习算法。如果这个偏差在实际数据中是合适（可以接受）的，那么NB将是首选。否则，逻辑回归将是首选。
• 我们可以把函数逼近学习算法看作是函数或条件分布\(P(Y|X)\)的统计估计。他们从训练数据样本中估计出\(P(Y|X)\)。与其他统计估计器一样，通过对不同样本的训练数据的偏差和预期方差来描述学习算法是有用的。