数据结构

分治

ST 表

ST 表是用倍增思想在 \(O(n\log n)\) 的预处理时间复杂度后用 \(O(1)\) 时间求区间 RMQ 的数据结构。我们记 \(f_{u,t}\) 表示区间 \([u,u+2^t)\) 的极值，然后通过递推式 \(f_{u,t}=\max / \min(f_{u,t-1},f_{u+2^{t-1},t-1})\) 就可以求出所有的 \(f\) 值，然后查询相当于两个长度为 \(2^{\lfloor \log n \rfloor}\) 的 \(f\) 值的极值。

code：

inline void build()
{
 for (int i = 1; i <= n; i++) st[i][0] = a[i];
 for (int j = 1; 1 + (1 << j) <= n; j++)
  for (int i = 1; i + (1 << j) - 1 <= n; i++)
   st[i][j] = max(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
inline int query(int l, int r)
{
 int t = log2(r - l + 1);
 return max(st[l][t], st[r - (1 << t) + 1][t]);
}

ST 表还有一种卡空间的写法，放在这里。

using poly = vector<int>;
struct table
{
 poly pos;
 vector<poly> f;
 int st[N], ed[N];
 inline void build()
 {
  int siz = pos.size(), lg = __lg(siz);
  f.resize(lg + 1);
  fo(i, 0, lg) f[i].resize(siz + 1);
  fo(i, 1, siz) f[0][i] = a[pos[i - 1]];
  fo(i, 1, lg) fo(j, 1, siz) if (j + (1 << i) - 1 <= siz) f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << i - 1)]);
  fo(i, 1, n) st[i] = ed[i] = -1;
  int j = 0;
  fo(i, 1, n)
  {
   if (pos.back() < i) break;
   while (pos[j] < i) ++j;
   st[i] = j + 1;
  }
  j = siz - 1;
  Fo(i, n, 1)
  {
   if (pos.front() > i) break;
   while (pos[j] > i) --j;
   ed[i] = j + 1;
  }
 }
 inline int qry(int l, int r)
 {
  int k = __lg(r - l + 1);
  return max(f[k][l], f[k][r - (1 << k) + 1]);
 }
} st;

维护信息特点

显然，如果 ST 表只能维护 RMQ 问题那是不是太弱了。于是我们发现区间 \(\gcd\) 也可以用 ST 表维护。那 ST 表维护的信息到底有什么特点呢？

满足结合律。我们需要保证算贡献的顺序对结果没有影响；
可重复贡献。发现 query 中有一部分的贡献是重复的。

这解释了为什么不能用 ST 表维护区间和。

笛卡儿树

主要用途是区间 RMQ。

如何维护

笛卡尔树每个节点维护两个值 \(k,w\)，其中 \(k\) 表示键值，\(w\) 表示值。在这个树上，\(k\) 满足 BST 性质，\(w\) 满足小根堆性质。

建树

我们按键值排序，然后每次当前节点肯定插在右链的最末端，于是我们用一个栈维护右链，考虑将一个节点插进来的时候，我们在栈中自顶向下找到第一个满足 \(w < w_i\) 的节点，当前节点作这个点的右儿子，剩下的所有节点当当前节点的左儿子，并且全部弹出栈，如果排序是 \(O(n)\) 的（大多情况是把下标当作 \(k\)），那么复杂度就是 \(O(n)\) 的。

code:

for (int i = 1; i <= n; i++)
{
 int k = top;
 while (k && a[stk[k]] > a[i]) --k;
 if (k) rs[stk[k]] = i;
 if (k < top) ls[i] = stk[k + 1];
 stk[++k] = i, top = k;
}

这样我们就能解释为什么笛卡尔树不是笛卡尔本人发明的却还要叫这个名字了？

感觉跟雷峰塔名字里有雷锋是因为乐于助人一样扯。

性质

对于一个以 \(u\) 为根节点的子树，我们可以知道 \(u\) 的子树构成了一个序列上的连续区间，这个区间满足最大（或最小）值是 \(u\) 的值，设这个区间是 \(S\)，且\(S\) 的任意连续子集，只要包含 \(u\)，那么这个区间最大（或最小）值肯定是 \(u\) 的值。

这个性质可以帮助我们迅速找出每个数作为 \(\max\) 管辖的区间，从而进行别的操作，例如这个题就利用了这样的性质进行分治。

线段树

线段树的具体操作就不再赘述了。

双半群结构

我们来看线段树维护的这个结构是什么样子的。

线段树每个节点上有一个标记信息，这些信息属于集合 \(T\)；
然后每个点自己还有一个信息，这些信息属于集合 \(D\)；
合并时有运算 \(*\) 满足 \(D*D\rightarrow D\)；
懒标记对当前节点的信息有影响。设运算方式为 @ 满足 \(D\) @ \(T \rightarrow D\)；
我们有标记复合运算 # 满足 \(T\) # \(T \rightarrow T\)。

那这样的系统要满足什么条件呢？

对于不同的区间的合并，不同的合并顺序并不影响结果。设三个区间维护的信息分别是 \(d_1,d_2,d_3\)，那么总应该有 \((d_1*d_2)*d_3=d_1*(d_2*d_3)\)，即满足结合律；
标记满足结合律：\((t_1\)#\(t_2)\)#\(t_3=t_1\)#\((t_2\)#\(t_3)\)；
\((t_1\)#\(t_2)@d=t_1@(t_2@d)\)；
\(t@(d_1*d_2)=(t@d_1)*(t@d_2)\)；
如果没有任何的标记，也就是说标记是空的，记为 \(\epsilon\)，满足 \(\epsilon @ d = d\)；
\(\epsilon\) # \(t=t\)。

数学中我们把配备了二元运算且满足结合律的结构叫做半群，于是我们发现：

所有信息，加上合并操作，构成半群；
所有标记，加上标记复合操作，构成半群。因其有单位元 \(\epsilon\)，所以它构成 幺半群；
标记会对信息有影响，这在数学中称作幺半群作用。

由此我们可以根据抽象数据结构的原理来维护线段树。

线段树维护矩阵

为什么线段树可以用来维护矩阵？

线段树维护矩阵的时候，信息和标记都是矩阵。对于常见的三种矩阵乘法 \((+,\times),(\min,+),(\max,+)\)，发现它们运算后的结果都是矩阵，也就是说对于信息和标记的运算都满足结合律、分配率、封闭性，且存在单位元，满足双半群性质，可以用线段树维护。

有了线段树维护矩阵之后，一些看似困难的问题也就有了漂亮的线性代数形式。

seg-beats

这是一种使用线段树维护区间最值操作以及维护区间历史最值的方法，来自 jiry_2 吉司机的国集论文，当然我会用矩阵解释其中一部分。

区间最值操作

区间最值操作指的是对区间取 \(\min\) 或取 \(\max\) 的操作，例题是 HDU5306. Gorgeous Sequence。考虑每个节点额外维护最大值 \(mx\)，次大值 \(se\) 和最大值出现次数 \(t\)，当我们找到区间 \([l,r]\) 时，如果 \(k\geq mx\) 就直接跳过去，如果 \(se<k<mx\) 此时所有最大值都被修改为 \(k\) 并且最大值个数不变，否则递归左右儿子。可以证明它的时间复杂度是 \(O(m\log n)\) 的，但是我不会，因为博客到这里并没有学会势能分析法。

inline void pushdown(int p)
{
 if (tag[p] == -1) return;
 if (fir[ls] > tag[p]) sum[ls] += 1ll * (tag[p] - fir[ls]) * cnt[ls], fir[ls] = tag[ls] = tag[p];
 if (fir[rs] > tag[p]) sum[rs] += 1ll * (tag[p] - fir[rs]) * cnt[rs], fir[rs] = tag[rs] = tag[p];
 tag[p] = -1;
}
void update(int p, int pl, int pr, int L, int R, int x)
{
 if (L <= pl && pr <= R && sec[p] < x)
 {
  if (fir[p] <= x) return;
  sum[p] -= 1ll * (fir[p] - x) * cnt[p], fir[p] = x, tag[p] = x;
  return;
 }
 int mid = (pl + pr) >> 1;
 pushdown(p);
 if (L <= mid) update(ls, pl, mid, L, R, x);
 if (R > mid) update(rs, mid + 1, pr, L, R, x);
 pushup(p);
}

沿用这一思路，我们可以做支持区间加减的区间最值操作问题，但是这不值得推广，尤其是在比赛中。换一种思路，我们发现这种做法本质上是把区间内元素分成最大值和非最大值两类分别维护。我们发现区间最大值操作只会标记在 \(se<k<mx\) 的区间节点上，可以看成只针对最大值的区间加减操作，于是分别维护最大值和非最大值两类的加减标记，下传的时候判断当前节点最大值是否为区间最大值即可。注意这样做是 \(O(m\log^2 n)\) 的，我们还是不会证。

然后我们考同时支持区间最大值和区间最小值的问题，例题是 BZOJ4695. 最假女选手（你也可以在 Luogu 上找到它）。我们延用上一个问题的操作，通过划分数域将区间最值转化成区间加减问题，对 max 和 min 分别做就可以了。

区间历史最值

从这里我要开始使用矩阵了，接下来请欣赏矩阵技术的表演。

区间加减维护区间历史最值

例题是 BZOJ3064 CPU 监控。对于每个节点我们维护 \([mx, hmx]\) 表示当前最大值和历史最大值，发现利用 \((+,\max)\) 矩阵可以列出操作的矩阵式子。

对于区间加操作，我们有

\[\begin{bmatrix}mx+x \\ hmx\end{bmatrix}=\begin{bmatrix}x & -\infty \\ -\infty & 0\end{bmatrix}\begin{bmatrix}mx\\hmx\end{bmatrix} \]

对于用 \(mx\) 更新 \(hmx\) 的操作，可以构造矩阵

\[\begin{bmatrix}mx\\\max(mx,hmx)\end{bmatrix}=\begin{bmatrix}0 & -\infty \\ 0 & 0\end{bmatrix}\begin{bmatrix}mx\\hmx\end{bmatrix} \]

这样规模较大，考虑缩减，发现只有利用加法改变这个值的时候 \(hmx\) 会改变，于是可以将两个矩阵缩减为

\[\begin{bmatrix}mx+x \\ \max(mx+x,hmx)\end{bmatrix}=\begin{bmatrix}x & -\infty \\ x & 0\end{bmatrix}\begin{bmatrix}mx \\ hmx\end{bmatrix} \]

进一步观察发现转移矩阵右边一列可以不维护，于是可以只维护左边的一列，只不过难以写为矩阵形式罢了。

结合区间最值后的历史最值问题

例题是【模板】线段树 3（区间最值操作、区间历史最值）。

同样利用矩阵。沿用区间最值问题的通用解法，对于最大值和非最大值，维护 \((+,\max/\min)\) 矩阵 \([mx,hmx]\) 和 \([se,smx]\) 以及标记，用上一个题的做法将区间加减操作集成到这里就可以了。

使用矩阵的时候要注意由于矩阵乘法自带的 \(O(k^2)\) 到 \(O(k^3)\) 的大常数可能会被卡，要不嫌麻烦地舍弃无用的维护信息转化为 tag 做，这也是为什么我这些题都没用矩阵写的原因。

猫树

鲜花：起这个名字是因为发明这个数据结构的人非常喜欢猫。

一类普遍的问题是给定序列 \(\{a_n\}\)，\(m\) 次询问一段 \([l,r]\) 的某种支持结合律和快速合并的信息，要求在线。下面假设合并复杂度为 \(O(1)\)，记 \(O(A)-O(B)-O(C)\) 从前到后分别表示预处理复杂度、单次询问复杂度和空间复杂度。

对于可减信息，直接用前缀和实现即可；对于可重复贡献的信息，长序列使用线段树 \(O(n)-O(\log n)-O(n)\) 解决，短序列多次询问使用 ST 表一类倍增倍增 RMQ \(O(n\log n)-O(1)-O(n\log n)\) 做，长序列多次询问建立笛卡尔树转化为 LCA 问题然后转为正负 1 RMQ 问题，然后使用四毛子一类科技做到 \(O(n)-O(1)-O(n)\)。上面的问题类型都有成熟的解法，但是对于仅支持结合律和快速合并的问题，例如最大子段和、区间段哈希值之类信息一般使用线段树，时间复杂度 \(O(n)-O(\log n)-O(n)\)，但是询问不够优秀，利用猫树可以做到 \(O(n\log n)-O(1)-O(n\log n)\)。

为了更快的询问，显然我们需要更劣的预处理复杂度来平衡。考虑一个询问 \([l,r]\)，如果 \(l=r\)，那么直接得到答案，否则考虑 \([l,r]\) 拆成线段树节点的时候，被哪个区间 \([pl,pr]\) 恰好包含，这等价于 \(pl\leq l\leq mid<r\leq pr\),如果我们预处理了线段树节点中 \([i,mid]\) 的信息和 \(prel(p,i)\) 与 \([mid+1,i]\) 的信息和 \(prer(p,i)\)，那么所求信息和就是 \(prel(p,l)+prer(p,r)\)，这一步是 \(O(n)\) 的，现在的问题是如何快速求出 \(p\)。

考虑一般情况下我们写的线段树，也就是左儿子编号为 p << 1，右儿子编号为 p << 1 | 1，那么 \([l,r]\) 定位的区间就是 \(l,r\) 两个叶子结点的 LCA，也就是这两个节点编号的二进制数的 LCP！只需要 x >> (int)log2(x ^ y)，也就是找出第一个不同的位置丢掉后边的，预处理 \(\log_2(n)\) 就可以 \(O(1)\) 求出 \(p\)，于是得到了 \(O(n\log n)-O(1)-O(n\log n)\) 的算法！

能不能更好？当然可以！这个方法来自参考文章的评论区。

我们将序列分块，块长 \(\log n\)，对于每一块建立猫树，再建一颗以块为单位的猫树，预处理时间复杂度 \(O(\dfrac{n}{\log n}\log n\log \log n+\dfrac{n}{\log n}\log\dfrac{n}{\log n})=O(n\log\log n)\)，查询复杂度 \(O(1)\)，非常优！！！并且不断套娃可以是复杂度越来越低，只不过常数会越来越大，并且会越来越难写，仅仅是这种方法就已经很难写了，但确实是应对某些毒瘤题的利器！

令人感到遗憾的一点是这种数据结构不支持修改，这是它们维护的数据信息特征决定的。

李超线段树

李超线段树主要作用是维护区间上的线段，操作有插入一条线段和查询某个点上最值。

每个节点上我们村的是当前区间的中间点最优的情况，这里用到了标记永久化思想（毕竟一次函数是变的，当前区间最优不一定是这个区间子区间的最优）。

对于插入操作，不妨设区间中点处新的更优，那么如果左端点新的反而比旧的劣，说明新旧两条线在左侧有交点，那就再去更新左侧，同理，如果右端点新的反而比旧的劣，更新右侧。

对于查询操作，注意因为有标记永久化，所以每一层都要取一个最优。

实现

#define D double
struct Line
{
 int id;
 D k, b;
 Line() {}
 Line(D x0, D y0, D x1, D y1, int _id)
 {
  id = _id;
  if (abs(x0 - x1) < eps) k = 0, b = max(y0, y1);
  else k = (y1 - y0) / (x1 - x0), b = y0 - k * x0;
 }
 D val(D x) { return k * x + b; }
};
Line t[M << 2];
void update(int p, int pl, int pr, int L, int R, Line g)
{
 if (L == pl && pr == R)
 {
  if (t[p].id == 0) return t[p] = g, void();
  int mid = (pl + pr) >> 1;
  if (abs(t[p].val(mid) - g.val(mid)) < eps)
  {
   if (t[p].id < g.id) swap(t[p], g);
  }
  else if (t[p].val(mid) < g.val(mid)) swap(t[p], g);
  int fl = (g.val(pl) + eps < t[p].val(pl));
  int fr = (g.val(pr) + eps < t[p].val(pr));
  if (fl && fr) return;
  if (!fl) update(ls(p), pl, mid, L, mid, g);
  if (!fr) update(rs(p), mid + 1, pr, mid + 1, R, g);
  return;
 }
 int mid = (pl + pr) >> 1;
 if (R <= mid) update(ls(p), pl, mid, L, R, g);
 else if (L > mid) update(rs(p), mid + 1, pr, L, R, g);
 else update(ls(p), pl, mid, L, mid, g), update(rs(p), mid + 1, pr, mid + 1, R, g);
}
Line query(int p, int pl, int pr, int pos)
{
 if (pl == pr) return t[p];
 int mid = (pl + pr) >> 1;
 Line ret;
 if (pos <= mid) ret = query(ls(p), pl, mid, pos);
 else ret = query(rs(p), mid + 1, pr, pos);
 if (abs(ret.val(pos) - t[p].val(pos)) < eps)
 {
  if (ret.id < t[p].id) return ret;
  return t[p];
 }
 else
 {
  if (ret.val(pos) > t[p].val(pos)) return ret;
  else return t[p];
 }
}

动态开点

=李超线段树+动态开点。

struct line
{
 int k, b;
 line() { k = 0, b = INF; }
 line(int _k, int _b) { k = _k, b = _b; }
 int f(int x) { return k * x + b; }
};
struct node
{
 int ls, rs;
 line l;
 int f(int x) { return l.k * x + l.b; }
 // 为什么这里要在节点内把 line 分开？
 // 因为 update 里的 swap 操作如果直接交换 tr[p] 和 g 会出错。
} tr[N];
int nc, rt;
void update(int &p, int pl, int pr, line g)
{
 if (!p) return tr[p = ++nc].l = g, void();
 int mid = (pl + pr) >> 1;
 if (tr[p].f(mid) > g.f(mid)) swap(tr[p].l, g);
 if (tr[p].l.k < g.k) update(tr[p].ls, pl, mid, g);
 else update(tr[p].rs, mid + 1, pr, g);
}
int query(int p, int pl, int pr, int k)
{
 if (!p) return INF;
 int mid = (pl + pr) >> 1;
 if (k <= mid) return min(tr[p].f(k), query(tr[p].ls, pl, mid, k));
 else return min(tr[p].f(k), query(tr[p].rs, mid + 1, pr, k));
}

应用

所有斜率优化的题都可以用李超线段树草过去！

为什么呢？因为斜率优化和李超线段树的区别不过是维护直线方式不同罢了，其他完全一样。

单侧递归线段树

又名：楼房重建线段树（来源是其例题），兔队线段树（因为粉兔致力于推广该方法）

例题：楼房重建（你也可以在 QOJ 上找到它，或者在 UR #19 前进四中发现它并写出 \(O(n\log^2 n)\) 的做法。）

题意相当于求前缀 \(\max\) 的个数。这里我们用线段树维护。

这里左区间对右区间有影响，我们考虑在 pushup 的时候维护一个 calc 函数，calc(p,v) 表示考虑到节点 \(p\)，前面对他的影响是 \(v\)，再算答案。

如果 \(v\geq mx_p\)，直接 return 0；

再如果 \(v \geq mx_{ls(p)}\)，递归右儿子 calc(rs(p),v)；

否则递归左儿子，结果是 calc(ls(p),v)+c[p]-c[ls(p)]。其中 \(c_p=c_{ls(p)}\) 表示的是右儿子在左儿子的影响下对答案的贡献。这是因为既然原来较大的 \(mx_{ls(p)}\) 都没对右边产生影响，那较小的 \(v\) 自然不会对右边产生影响。

code:

int n, m, c[N << 2];
double mx[N << 2];
int calc(int p, int pl, int pr, double v)
{
 if (v >= mx[p]) return 0;
 if (pl == pr) return (mx[p] > v);
 int mid = (pl + pr) >> 1;
 if (mx[ls(p)] <= v) return calc(rs(p), mid + 1, pr, v);
 else return calc(ls(p), pl, mid, v) + c[p] - c[ls(p)];
}
void update(int p, int pl, int pr, int pos, int v)
{
 if (pl == pr)
 {
  mx[p] = 1.0 * v / pos, c[p] = 1;
  return;
 }
 int mid = (pl + pr) >> 1;
 if (pos <= mid) update(ls(p), pl, mid, pos, v);
 else update(rs(p), mid + 1, pr, pos, v);
 mx[p] = max(mx[ls(p)], mx[rs(p)]);
 c[p] = c[ls(p)] + calc(rs(p), mid + 1, pr, mx[ls(p)]);
}

这个 trick 越来越常用了啊。

线段树分治

算是线段树的一个常用应用。思想类似于线段树优化建图，核心思路是在时间维建立线段树把每个修改存在的区间拆到线段树节点上，最后在线段树上用 \(\text{polylog}(n)\) 的复杂度把查询一起解决。

线段树分治最常见的应用场景是在动态图的问题中，例如洛谷上的模板题和离线可过的动态图连通性问题，一般配合可撤销并查集维护。

平衡树

平衡树维护信息的特征其实和线段树是一样的，只不过是在加上区间反转操作之后就不能用线段树了，因为线段树没有办法交换两个儿子。

Splay

节点维护信息

rt ：根节点
tot ：节点个数
val[p] ：节点的权值
siz[p]：节点子树大小
fa[p]：父亲节点的编号
ch[p][0/1] ：左儿子和右儿子的编号

下面的讲解中，我们设 \(p\) 表示当前节点，\(f\) 表示 \(p\) 的父亲，\(g\) 表示 \(f\) 的父亲。

基本操作

pushup：更新节点子树大小
get：判断这个节点是一个右儿子还是一个左儿子
clear:删掉当前节点

实现：

void pushup(int p) { siz[p] = siz[ch[p][0]] + siz[ch[p][1]] + cnt[p]; }
bool get(int p) { return p == ch[fa[p]][1]; }
void clear(int p) { siz[p] = ch[p][0] = ch[p][1] = val[p] = fa[p] = cnt[p] = 0; }

旋转操作

旋转操作分为左旋和右旋，左旋可以看做右旋的逆过程，所以这里只讲解右旋。我们要求旋转之后，当前节点 \(p\) 的深度减一，而这棵树仍然满足 BST 性质。

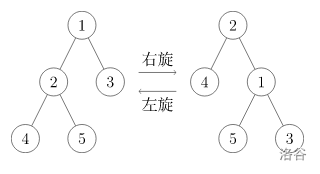
旋转过程：

将 \(p\) 的右儿子接到 \(f\) 的左儿子上，将 \(f\) 接到 \(p\) 的右儿子上
如果 \(g\) 存在，用 \(p\) 来填上 \(f\) 原来的位置
更新 \(f\) ，\(p\)

实现：

void rotate(int p)
{
 int f = fa[p], g = fa[f], chk = get(p);
 ch[f][chk] = ch[p][chk ^ 1];
 if (ch[p][chk ^ 1]) fa[ch[p][chk ^ 1]] = f;
 ch[p][chk ^ 1] = f, fa[f] = p, fa[p] = g;
 if (g) ch[g][f == ch[g][1]] = p;
 pushup(f), pushup(p);
}

Splay 操作

Splay 操作规定：每一次旋转之后，都要将节点 \(p\) 旋至根节点。

Splay 操作就是对 \(p\) 做多次 Splay 步骤。每对 \(p\) 做一次 Splay 步骤，\(p\) 到 \(rt\) 的距离就减一。Splay 步骤分三种，具体有 6 种操作。分类很繁杂难理解，但代码很好写。

先把实现放上：

void splay(int p)
{
 for (int f = fa[p]; f = fa[p], f; rotate(p))
  if (fa[f]) rotate(get(p) == get(f) ? f : p);
 rt = p;
}

你没看错，这么短的代码，蕴含了 3 种复杂操作和十分复杂的复杂度分析。我们来分析这三种操作。

zig：将 \(p\) 直接左旋或右旋。这个操作用于 \(f=rt\) 时，这样就可以直接把 \(p\) 旋转到 \(rt\)。
zig-zig：当 \(f\) 不是根节点，而 \(chk(f)=chk(p)\) 时，我们先将 \(g\) 左旋或右旋，再将 \(p\) 左旋或右旋。
zig-zag：使用条件就是上面两种都不适用的时候。我们将 \(p\) 先左旋再右旋或先右旋后左旋。

手摸一下就可以理解这 3 种操作。至于上面说的 6 种，是因为有左旋和右旋的区别，我们在 rotate 里已经解决掉了。

剩下的操作就是次要的了，可以用递归实现。这里直接放代码。

void nw(int k, int fath, int op) { val[++tot] = k, siz[tot] = cnt[tot] = 1, fa[tot] = fath, ch[fath][op] = tot; }
void ins(int k)
{
 if (!rt) return val[++tot] = k, cnt[tot]++, rt = tot, pushup(rt);
 int cur = rt, f = 0;
 while (true)
 {
  if (val[cur] == k)
  {
   cnt[cur]++, pushup(cur), pushup(f), splay(cur);
   break;
  }
  f = cur, cur = ch[cur][val[cur] < k];
  if (!cur)
  {
   val[++tot] = k;
   cnt[tot]++, fa[tot] = f, ch[f][val[f] < k] = tot;
   pushup(tot), pushup(f), splay(tot);
   break;
  }
 }
}
int rk(int k)
{
 int p = rt, res = 0;
 while (true)
 {
  if (k < val[p]) p = ch[p][0];
  else
  {
   res += siz[ch[p][0]];
   if (!p) return res + 1;
   if (val[p] == k) return splay(p), res + 1;
   res += cnt[p], p = ch[p][1];
  }
 }
}
int prev()
{
 int p = ch[rt][0];
 if (!p) return p;
 while (ch[p][1]) p = ch[p][1];
 return splay(p), p;
}
int next()
{
 int p = ch[rt][1];
 if (!p) return p;
 while (ch[p][0]) p = ch[p][0];
 return splay(p), p;
}
void del(int k)
{
 rk(k);
 if (cnt[rt] > 1) return --cnt[rt], pushup(rt), void();
 if (!ch[rt][0] && !ch[rt][1]) return clear(rt), rt = 0, void();
 if (!ch[rt][0])
 {
  int cur = rt;
  return rt = ch[rt][1], fa[rt] = 0, clear(cur), void();
 }
 if (!ch[rt][1])
 {
  int cur = rt;
  return rt = ch[rt][0], fa[rt] = 0, clear(cur), void();
 }
 int cur = rt, x = prev();
 fa[ch[cur][1]] = x, ch[x][1] = ch[cur][1], clear(cur), pushup(rt);
}
int kth(int k)
{
 int p = rt;
 while (1)
 {
  if (ch[p][0] && k <= siz[ch[p][0]]) p = ch[p][0];
  else
  {
   k -= cnt[p] + siz[ch[p][0]];
   if (k <= 0) return splay(p), val[p];
   p = ch[p][1];
  }
 }
}

时间复杂度分析

我们运用势能分析法（参考资料：势能分析法-Dfkuaid（没错时间复杂度相关的记号只要没有说明就和他一样，别问我为什么））求时间复杂度。

约定 \(\operatorname{subtree}(x)\) 表示点 \(x\) 在 splay 上的子树这一个点集，\(|x|=|\operatorname{subtree(x)}|\)，记 \(p\) 旋转之后的点为 \(p'\) 用来区分。

感性理解势能就是说对于每个数据结构，有的操作可能为后面的操作积累了势能，也就是说后面操作代价可能变大，也可能为后面操作消耗了势能，也就是说后面操作代价可能变小。

定义势能函数 \(\Phi(p)=\sum_{x\in\operatorname{subtree}(p)}f(x)\)，其中 \(f(x)=\log |x|\)，对于 \(p,f,g\) 三点一线的情况，\(\Phi_{i}-\Phi_{i-1}\leq f_i(p)+f_i(g)-2f_{i-1}(f)\)。我们观察树的结构，发现 \(|p'|\geq |p|+|g'|\)，于是可得 \(f_{i-1}(p)+f_{i-1}(g)-2f_{i}(p)=\log |p|+\log |g|-2\log |p'|=\log \frac{|p||g|}{|p'|^2}\leq \log \frac{|p||g|}{(|p|+|g'|)}\leq -1\)，于是 \(\hat c_i=c_i+\Phi(i)-\Phi(i-1)=1+3(f_i(p)-f_{i-1}(p))-1=3\cdot(f_{i}(p)-f{i-1}(p))\)。对于三点不共线的情况，同理可得（我很懒）\(\hat c_i\leq 2\cdot(f_i(p)-f_{i-1}(p))\)。对于直接旋转到根的情况，\(\hat c_i=1+f_i(x)-f_{i-1}(x)\)。于是单次 splay 的时间复杂度为 \(O(1+f_k(p)-f_0(p))\leq O(\log n)\)。

于是 \(\sum c_i=\sum \hat c_i + \Phi(D_0)-\Phi(D_n)=O(m\log n)\)，又根据势函数的定义，\(-n\log n\leq \Phi(D_0)-\Phi(D_m)\leq n\log n\)，于是 \(\sum c_i=O((n+m)\log n)\)。

无旋 Treap（FHQ-Treap）

FHQ-Treap 是由范浩强发明的不用旋转的 Treap，其不用旋转的性质可以帮助我们进行可持久化操作。

作为 Treap，FHQ-Treap 的每个点都记录一个优先级 pri 和其权值 val，其中 pri 满足二叉堆的性质，val 满足 BST 性质，其中 pri 是随的。这样做能平衡的原因是数据范围越大，随机出来一条链的可能性就越小，也就是说树的形态越平衡，至于小数据，平不平衡就无所谓了。

FHQ-Treap 的核心操作为分裂与合并。

分裂操作

分裂操作分为按排名合并与按大小合并。这里只讲按大小分裂。假设当前节点为 \(u\)，split 的参考值是 \(x\)，分裂后两棵树是 \(L\) 和 \(R\)，如果 \(val(x)\le x\),那么 \(u\) 的左儿子一定在 \(L\) 上，于是我们把 \(u\) 接到 \(L\) 上，递归右儿子，\(R\) 不变，下一层如果要接到 \(L\) 上，那么让它接到 \(u\) 的右儿子上，这个可以用传参来维护，反之亦然。这里的传参相当于给后来人留接口，告诉他们分裂之后当谁的儿子。

void split(int u, int x, int &L, int &R)
{
 if (!u) return L = R = 0, void();
 if (t[u].val <= x) L = u, split(t[u].rs, x, t[u].rs, R);
 else R = u, split(t[u].ls, x, L, t[u].ls);
 pushup(u);
}

合并操作

设这两棵树是 \(L\) 和 \(R\)，如果两者有一个是空的，那么返回不空的那一个；如果 \(L\) 的 \(pri\) 小于 \(R\) 的，我们就让 \(L\) 的右儿子和 \(R\) 合并，然后接到 \(L\) 的右儿子上，更新 \(L\)，反之亦然。

int merge(int L, int R)
{
 if (!L || !R) return L | R;
 if (t[L].pri <= t[R].pri) return t[L].rs = merge(t[L].rs, R), pushup(L), L;
 else return t[R].ls = merge(L, t[R].ls), pushup(R), R;
}

然后其他操作就迎刃而解了。还是直接放代码。

inline void Insert(int x) { newnode(x), split(rt, x, L, R), rt = merge(merge(L, cnt), R); }
inline void Delete(int x)
{
 split(rt, x - 1, L, R), split(R, x, p, R);
 p = merge(t[p].ls, t[p].rs), rt = merge(merge(L, p), R);
}
inline int get_rank(int x)
{
 split(rt, x - 1, L, R);
 int y = t[L].siz + 1;
 rt = merge(L, R);
 return y;
}
inline int get_val(int u, int k)
{
 int now = u;
 while (now)
 {
  int x = t[t[now].ls].siz + 1;
  if (x == k) return t[now].val;
  if (x < k) now = t[now].rs, k -= x;
  else now = t[now].ls;
 }
}
inline int get_pre(int x)
{
 split(rt, x - 1, L, R);
 int y = get_val(L, t[L].siz);
 rt = merge(L, R);
 return y;
}
inline int get_nxt(int x)
{
 split(rt, x, L, R);
 int y = get_val(R, 1);
 rt = merge(L, R);
 return y;
}

K-D Tree

原理

KDT 是基于空间分割的树形数据结构，用来维护高维的信息，是平衡的二叉搜索树，树高严格 \(O(\log n)\)，每个节点表示数据中一个高维点，其每个子树表达该子树内所有点的 \(k\) 维正交包围盒，左右子树范围不相交，一般每个节点还要记录这个包围盒。

因为应用的时候 \(k\) 都小的可怜，所以时间复杂度分析的时候 \(k\) 作常数直接扔掉。

KDT 的静态构建是容易的，我们采用中位数循环切割的方式，对于当前的点集，我们以第 \(dep\bmod k\) 维为依据划分，将中位数上的点作为子树的根，左边的扔到左儿子，右边的扔到右儿子。选取中位数我们使用 std::nth_element(p+pl,p+mid,p+pr+1,cmp) 即可 \(O(pr-pl+1)\) 实现左右儿子的拆分，时间复杂度 \(T(n)=2T(n/2)+O(n)=O(n\log n)\)。

然后我们就能解决不带修查询的问题了。在树上递归，如果当前节点对应的包围盒与查询区间没有交集就直接不走，如果当前节点被查询包围盒完全包含就直接加上当前的权值,否则判断当前点的情况然后递归左右儿子。这样做时间复杂度是 \(O(n^{1-\frac{1}{k}})\) 的，因为这只受部分被查询的包围盒包含的那一部分的影响，假设查询的包围盒是 \(R\)，我们在 \(k\) 维上按当前节点划分的标准能把 \(R\) 分成 \(2^k\) 个小部分，用于划分的超平面最多跨过 \(2^{k-1}\) 个部分，所以 \(T(n)=2^{k-1}T(n/2^k)+O(1)=O(n^{1-\frac{1}{k}})\)。

动态构建就需要一点心机了。一般会使用替罪羊树暴力重构，但这样的话由于大部分人会把 \(\alpha\) 设为 \(0.75\) 左右，那么树高就变成了 \(\log_{4/3}(n)+O(1)\) 是原来的两倍还要多，复杂度基本上成 \(O(n)\) 了，很坏。使用根号重构可以做到 \(O(\sqrt{n\log n})+n^{1-\frac{1}{k}}\)，更优的做法是使用二进制分组，维护若干棵 2 的自然数次幂的 KDT，插入的时候新增一颗大小为 1 的 KDT，然后不断将相同大小的树合并，实现起来是 \(O(n\log^2 n)\) 的，查询复杂度还是 \(O(n^{1-\frac{1}{k}})\)。

应用

正交查询

也就是查询一个包围盒里面的信息的和，KDT 作为 BST 也要求信息满足双半群性质。

欧式聚类

聚类就是将样本集 \(D\) 分成若干个互不相交的簇的过程，结果要求簇内相似度高且簇间相似度低，是“无监督学习”的重要组成部分。相似度一般用“距离”来衡量，其中“距离”的定义为作用在样本上的二元函数 \(\text{dist}:(\mathbf{x_1},\mathbf{x_2})\mapsto a\) 满足：

非负性：\(\text{dist}(\mathbf{x_i,x_j})\geq 0\)
同一性：\(\text{dist}(\mathbf{x_i,x_j})=0\) 当且仅当 \(\mathbf{x_i}=\mathbf{x_j}\)
对称性：\(\text{dist}(\mathbf{x_i,x_j})=\text{dist}(\mathbf{x_j,x_i})\)
直递性：\(\text{dist}(\mathbb{x_i,x_j})\leq\text{dist}(\mathbf{x_i,x_k})+\text{dist}(\mathbf{x_k,x_j})\)

欧式聚类就是 \(\text{dist}\) 函数是欧几里得距离的时候的聚类划分，当然也可以扩展到更多中距离如闵可夫斯基距离/曼哈顿距离。实现方法大致来说是：先随便选择一个点 \(p_{11}\)，确定阈值 \(r\)，KDT 找到离这个点距离最小的 \(n\) 个点，把距离小于等于 \(r\) 的点 \(p_{12},p_{13},\dots\) 放进 \(Q(p_{11})\)，然后在 \(Q(p_{11})\) 中找到点 \(p_{12}\) 重复上面的过程，找到 \(p_{22},p_{23},\dots\)，全放进 \(Q\) 里面，当 \(Q\) 没有新点可以加入就停止这一轮，再做下一轮。

实现

这样基础操作就差不多了，关键在于 KDT 要如何写。我写了一个 BST-style 维护分治信息的 KDT，Leafy-style 也是可以的。

const int N = 1e5 + 5, K = 20;
using pt = array<int, K>;
bool operator<=(const pt &a, const pt &b)
{
 for (int i = 0 ; i < K; ++i) if (a[i] > b[i]) return false;
 return true;
}
bool operator<(const pt &a, const pt &b)
{
 for (int i = 0; i < K; ++i) if (a[i] >= b[i]) return false;
 return true;
}
int n, k, rt[K], m, cnt;
struct info {} I0, a[N];
struct Tag {} T0;
info operator+(const info &a, const info &b) { ; }
info operator+(const info &a, const Tag &b) { ; }
Tag operator+(const Tag &a, const Tag &b) { ; }
bool operator==(const Tag &a, const Tag &b) { return true; }
struct treenode
{
 int lc, rc;
 pt mx, mn, now;
 info t = I0, sum = I0;
 Tag tag = T0;
} tr[N];
pt p[N];
inline void up(int rt)
{
 tr[rt].mx = tr[rt].mn = tr[rt].now, tr[rt].sum = tr[rt].t;
 if (tr[rt].lc)
 {
  tr[rt].sum = tr[rt].sum + tr[tr[rt].lc].sum;
  for (int i = 0; i < k; ++i) tr[rt].mx[i] = max(tr[rt].mx[i], tr[tr[rt].lc].mx[i]);
  for (int i = 0; i < k; ++i) tr[rt].mn[i] = min(tr[rt].mn[i], tr[tr[rt].lc].mn[i]);
 }
 if (tr[rt].rc)
 {
  tr[rt].sum = tr[rt].sum + tr[tr[rt].rc].sum;
  for (int i = 0; i < k; ++i) tr[rt].mx[i] = max(tr[rt].mx[i], tr[tr[rt].rc].mx[i]);
  for (int i = 0; i < k; ++i) tr[rt].mn[i] = min(tr[rt].mn[i], tr[tr[rt].rc].mn[i]);
 }
}
inline void spread(int rt)
{
 if (tr[rt].tag == T0) return;
 tr[tr[rt].lc].t = tr[tr[rt].lc].t + tr[rt].tag;
 tr[tr[rt].rc].t = tr[tr[rt].rc].t + tr[rt].tag;
 tr[tr[rt].lc].sum = tr[tr[rt].lc].sum + tr[rt].tag;
 tr[tr[rt].rc].sum = tr[tr[rt].rc].sum + tr[rt].tag;
 tr[tr[rt].lc].tag = tr[tr[rt].lc].tag + tr[rt].tag;
 tr[tr[rt].rc].tag = tr[tr[rt].rc].tag + tr[rt].tag;
 tr[rt].tag = T0;
}
int build(int pl, int pr, int d = 0)
{
 if (pl > pr) return 0;
 int mid = (pl + pr) >> 1, rt = mid;
 nth_element(p + pl, p + mid, p + pr + 1, [d](int i, int j) { return p[i][d] < p[j][d]; });
 tr[rt].now = p[mid], tr[rt].t = a[mid];
 tr[rt].lc = build(pl, mid, (d + 1) % k);
 tr[rt].rc = build(mid + 1, pr, (d + 1) % k);
 return up(rt), rt;
}
void update(int rt, pt L, pt R, Tag d)
{
 if (L <= tr[rt].mn && tr[rt].mx <= R)
 {
  tr[rt].t = tr[rt].t + d;
  tr[rt].tag = tr[rt].tag + d;
  tr[rt].sum = tr[rt].sum + d;
  return;
 }
 if (tr[rt].mx < L || R < tr[rt].mn) return;
 spread(rt);
 if (L <= tr[rt].now && tr[rt].now <= R) tr[rt].t = tr[rt].t + d, tr[rt].tag = tr[rt].tag + d;
 if (tr[rt].lc) update(tr[rt].lc, L, R, d);
 if (tr[rt].rc) update(tr[rt].rc, L, R, d);
 up(rt);
}
info query(int rt, pt L, pt R)
{
 if (!rt || tr[rt].mx < L || R < tr[rt].mn) return I0;
 if (L <= tr[rt].mn && tr[rt].mx <= R) return tr[rt].sum;
 spread(rt);
 info ans = I0;
 if (L <= tr[rt].now && tr[rt].now <= R) ans = tr[rt].t;
 return query(tr[rt].lc, L, R) + ans + query(tr[rt].rc, L, R);
}
void append(int &rt)
{
 if (!rt) return;
 p[++cnt] = tr[rt].now;
 append(tr[rt].lc), append(tr[rt].rc);
 rt = 0;
}
signed main()
{
 cin >> n >> k >> m;
 for (int i = 1; i <= n; ++i)
  for (int j = 0; i < k; ++j) cin >> p[i][j];
 build(1, n);
 // dynamic build
 while (m--)
 {
  pt now;
  for (int j = 0; j < k; ++j) cin >> now[j];
  p[cnt = 1] = now;
  for (int sz = 0; true; ++sz)
   if (!rt[sz])
   {
    rt[sz] = build(1, cnt);
    break;
   }
   else append(rt[sz]);
 }
 return 0;
}

动态树

LCT

闲话：没错，这玩意是 Tarjan 发明的。

思想

我们需要动态维护连边删边以及修改点权，并且维护路径上的权值。如果没有连边删边的操作，可以利用重链剖分解决问题。而在加上删边加边的操作后，重链剖分变得不靠谱，因为每个节点的 siz 是随时变化的。我们想要一个更为稳定的剖分方式。

这里引入~~失恋剖分~~实链剖分的概念。对于每一个点的子树内与之直接相连的边中，选出一条边作为“实边”，其余的边称为“虚边”，由实边组成的链我们称之为实链。实链剖分对树的形态的依赖相较于重链剖分来说要更小一点。我们把树剖开，为了方便维护每条实链上的信息，我们使用 splay（等评测机升级是不是也能用 FHQ-Treap 了啊）。为了把这些 splay 组织起来，我们构造一个辅助树(Aux Tree)的结构。

为了保证时间复杂度是 \(\log\) 的，splay 会对实链的结构进行一些改变，而为了让原树的结构能在辅助树中体现出来，我们需要满足：辅助树中序遍历得到的，对应实链从上到下。对于虚边，我们不能同时记父子而导致分不出实边虚边，这里我们记父不记子，也就是说 splay 上的叶子结点没有儿子，这很好。

操作与实现

以【模板】动态树 (LCT) 为例，变量声明与 splay 几乎一样。

基础的部分例如合并子树信息、标记下传就直接放了。

inline void pushup(int p) { sum[p] = sum[ch[p][0]] ^ val[p] ^ sum[ch[p][1]]; }
inline void reverse(int p) { swap(ch[p][0], ch[p][1]), tag[p] ^= 1; }
inline void pushdown(int p)
{
 if (!tag[p]) return;
 reverse(ch[p][0]), reverse(ch[p][1]), tag[p] = 0;
}
inline void push(int p)
{
 if (!is_root(p)) push(fa[p]);
 pushdown(p);
}

一部分代码是与 splay 重合的：

inline int get(int p) { return ch[fa[p]][1] == p; }
inline bool is_root(int p) { return ch[fa[p]][0] != p && ch[fa[p]][1] != p; }
inline void rotate(int p)
{
 int f = fa[p], g = fa[f], k = get(p);
 if (!is_root(f)) ch[g][get(f)] = p;
 ch[f][k] = ch[p][k ^ 1], fa[ch[p][k ^ 1]] = f;
 ch[p][k ^ 1] = f, fa[f] = p, fa[p] = g;
 pushup(f), pushup(p);
}
inline void splay(int p)
{
 push(p); // 注意先把 p 上面的一部分的标记全清掉
 for (int f; f = fa[p], !is_root(p); rotate(p))
  if (!is_root(f)) rotate(get(p) == get(f) ? f : p);
}

access 操作的作用就是打通一条原树的根到当前点的实链。我们不断把 \(p\) 旋到当前实链的根上，然后跳到父亲上，直到世界尽头(bushi，这体现出“记父不记子”的合理性。

inline void access(int p)
{
 for (int child = 0; p; child = p, p = fa[p]) splay(p), ch[p][1] = child, pushup(p);
}

makeroot 操作的作用是把 \(p\) 变成原树的根，具体方法就是打通 \(p\) 到根的实链，然后旋上去。最后因为 access 操作会让它在原树树根所在的 splay 的最右点，但是根需要在最左点，所以还得 reverse 一下。

inline void makeroot(int p) { access(p), splay(p), reverse(p); }

split 操作把 \(u\) 到 \(v\) 的路径分裂出来，操作是把 \(u\) 扔到根上，打通 \(u\) 到 \(v\) 的实链，一般我们需要让 \(v\) 作根，所以旋一下就行了。

inline void split(int u, int v) { makeroot(u), access(v), splay(v); }

findroot 找到当前点所在实链的顶。

inline int findroot(int p)
{
 access(p), splay(p), pushdown(p);
 while (ch[p][0]) p = ch[p][0], pushdown(p);
 return splay(p), p;
}

link 操作和 cut 操作搞就完了。

inline void link(int u, int v) { makeroot(u), fa[u] = v; }
inline void cut(int u, int v)
{
 makeroot(u);
 if (findroot(v) == u && fa[v] == u && !ch[v][0]) fa[v] = ch[u][1] = 0, pushup(u);
}

分块

分块思想

分成 \(\sqrt n\) 块，大段维护，小段暴力。

为什么是 \(\sqrt n\) 块？我们不妨设分了 \(B\) 段，那么大段维护的时间复杂度是 \(O(\frac{n}{B})\)，小段暴力的复杂度是 \(O(B)\)，总复杂度 \(O(\frac{n}{B}+B)\)，由均值不等式我们知道当 \(\frac{n}{B}=B\) 时时间复杂度取最小值，此时 \(B=\sqrt n\)，于是总的时间复杂度就是 \(O(n\sqrt n)\)。

实现

一般地，我们记下每个块的左端点与右端点，以及每个点所属的块的编号，提前预处理。

block = sqrt(n);
for (int i = 1; i <= block; i++) st[i] = (i - 1) * block + 1, ed[i] = i * block;
if (ed[block] < n) ed[block] = n;
for (int i = 1; i <= block; i++)
 for (int j = st[i]; j <= ed[i]; j++) pos[j] = i, sum[i] += a[j];

应用：Method of Four Russians

俗称四毛子算法，大概是由四个俄罗斯人提出的。这是一种 \(O(n)-O(1)\) 解决区间 \(\text{RMQ}\) 问题的方法，时间复杂度很优，但常数不小。分块思想在其中的体现在于解决 \(+1-1 RMQ\) 问题，也就是每两个数差的绝对值为 1 的序列的 RMQ 问题，其具体方法为：

设定阈值 \(B\)，把序列分为 \(\frac{n}{B}\) 块，用 ST 表预处理整块之间的极值，复杂度为 \(O(\frac{n}{b}\log \frac{n}{b})=O(n)\)，散块维护块内前缀最值就行了，时间复杂度 \(O(n)\)。难的，巧的是端点在同一块内。注意到差分数组可以用二进制维护，于是预处理每种差分序列的最优解，时间复杂度 \(O(2^{\log n\log n)<O(n)\)，这样就做到 \(O(n)-O(1)\) 了。

但是一般的序列并不满足这样的性质，于是四毛子先建出原序列的笛卡尔树，然后拿欧拉序做，这样就能用上面的做法做了。

莫队

普通莫队算法

例题：P3901 数列找不同

考虑最基础的暴力，就是离线下来，然后不断挪左右端点，然后每次就是 \(O(n)\)，稳 TLE。

莫队就是把 \(\{a_n\}\) 分块，然后对于每个区间，以左端点所属块的编号为第一关键字，右端点为第二关键字排序，然后再进行一边上面的暴力。时间复杂度 \(O(n\sqrt n)\)，可过。

实现

struct que
{
 int l, r, id;
 bool operator<(const que &b)const
 {
  if(bel[l] == bel[b.l]) return r < b.r;
  return bel[l] < bel[b.l];
 }
} q[N];
void move(int now, int op){...}
void solve()
{
 int block = sqrt(n);
 sort(q + 1, q + 1 + m);
 int l = 1, r = 0;
 for(int i = 1; i <= m; i++)
 {
  while(l > q[i].l) move(--pl, 1);
  while(r < q[i].r) move(++pr, 1);
  while(l < q[i].l) move(pl++, -1);
  while(r > q[i].r) move(pr--, -1);
  ans[q[i].id] = nowAns;
 }
}

注意这四个指针挪动的顺序不能变。

复杂度证明

考虑几何方式。我们把暴力和莫队的图都画出来。

暴力：

莫队：

我们发现莫队移动的总量被严格控制在 \(O(n\sqrt{n})\) 之内，所以时间复杂度就是 \(O(n\sqrt n)\) 的。

奇偶段优化

我们来看一组数据（来自 OI-Wiki）：

// 设块的大小为 2 (假设)
1 1
2 100
3 1
4 100

手摸发现 \(r\) 指针挪了 300 次，非常不好，这里使用奇偶段优化。我们考虑奇数编号的块里 \(r\) 从大到小排序，偶数块内 \(r\) 从小到大排序，这样就可以保证块与块之间不会有突变了。

实现

struct query
{
 int l, r, id;
 bool operator<(const query &b) const
 {
  if (bel[l] != bel[b.l]) return l < b.l;
  if (bel[l] & 1) return r < b.r;
  return r > b.r;
 }
} q[N];

扫描线

相信对于大多数 OIer 来说，初始扫描线都是在矩形面积并上，我们通过让一条线沿一条坐标轴扫的方式把二维的问题转化成了一维的问题。这启发我们，对于三次乃至更高次的问题，我们在一开始都可以利用扫描线把维度降低，然后再去想剩下的。

这里放一下模板题的代码，因为我模拟赛的时候忘了。

#include <algorithm>
#include <cstdio>
#define N 1000005
#define ls(p) (p * 2)
#define rs(p) (p * 2 + 1)
#define int long long
using namespace std;
int n, cnt, xx[N << 2], ans;
struct Line { int y, lx, rx, io; } e[N << 2];
void mkL(int yy, int x1, int x2, int io) { e[++cnt].y=yy; e[cnt].lx = x1, e[cnt].rx = x2; e[cnt].io=io; }
bool cmp(Line a, Line b) { return a.y < b.y; }
struct Node { int tag, length; } t[N];
void pushup(int p, int pl, int pr)
{
 if (t[p].tag) t[p].length = xx[pr] - xx[pl];
 else if (pl + 1 == pr) t[p].length = 0;
 else t[p].length = t[ls(p)].length + t[rs(p)].length;
}
void update(int L, int R, int p, int pl, int pr, int type)
{
 if (L <= pl && pr <= R) { t[p].tag += type; pushup(p, pl, pr); return;	}
 if (pl + 1 == pr) return;
 int mid = (pl + pr) / 2;
 if (L <= mid) update(L, R, ls(p), pl, mid, type);
 if (R > mid) update(L, R, rs(p), mid, pr, type);
 pushup(p, pl, pr);
}
signed main()

 scanf("%lld", &n);
 for (int i = 1; i <= n; i++)
 {
  int x1, y1, x2, y2;
  scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2);
  mkL(y1, x1, x2, 1); xx[cnt] = x1;
  mkL(y2, x1, x2, -1); xx[cnt] = x2;
 }
 sort(xx + 1, xx + 1 + cnt);
 int num = unique(xx + 1, xx + 1 + cnt) - (xx + 1);
 sort(e + 1, e + 1 + cnt, cmp);
 for(int i = 1; i <= cnt; i++)
 {
  ans += t[1].length * (e[i].y - e[i-1].y);
  int L = lower_bound(xx + 1, xx + 1 + num, e[i].lx) - xx;
  int R = lower_bound(xx + 1, xx + 1 + num, e[i].rx) - xx;
  update(L, R, 1, 1, num, e[i].io);
 }
 printf("%lld", ans);
 return 0;
}

posted @ 2024-11-21 17:05 lhc0707 阅读(54) 评论(0) 收藏举报

刷新页面返回顶部

lhc0707