混凝土

记号约定

• \(\ln x\)：自然对数 \(\log_ex\)
• \(\lg x\)：以十为底的对数 \(\log_{10} x\)
• \(\log x\)：以二为底的对数 \(\log_{2}x\)
• \(\lfloor x\rfloor\)：\(\max\{n \in \mathbb Z|n\leq x\}\)
• \(\lceil x\rceil\)：\(\min\{n\in \mathbb Z|n \geq x\}\)
• \(x\bmod y\)：\(x-y\lfloor\frac{x}{y}\rfloor\)
• \(\{x\}\)：\(x \bmod 1\)
• \(\sum f(x) \delta x\)：无限和式
• \(\sum_{a}^b f(x) \delta x\)：有限和式
• \(a \perp b\)：\(\gcd(a,b)=1\)
• \(\# S\)：\(S\) 集合的元素个数。
• \([P]\)：当 \(P\) 为真时值为 \(1\)，否则值为 \(0\)

第一章 递归问题

1. 汉诺塔问题

三个柱, 第一个柱上有 \(n\) 个圆盘, 圆盘大小从上到下递增, 每次只能移动一个圆盘, 每根柱子上圆盘大小应时刻满足从上到下递增,求最小方案数.

命名并求解. 设 \(T(n)\): 圆盘数为 \(n\) 的最小步骤. 问题相当于将 \(n-1\) 个圆盘挪到中间的柱上, 再将第 \(n\) 块圆盘扔到第 \(n\) 个柱上, 然后把这 \(n\) 个挪到最后的柱子上. 可得出递推式: \(T(n)=T(n-1)+1+T(n-1)=2T(n-1)+1\). 可以求出 \(T(n)=2^n-1\).

2. 直线割平面问题.

平面上 \(n\) 条直线最多能将平面分成几部分.

每新增一条直线最多产生 \(n-1\) 个交点, 分出 \(n\) 个平面, 故 \(f(n)=f(n-1)+n\), 则 \(f(n)=\sum_{k=1}^n k=\frac{n(n+1)}{2}\).

3. 约瑟夫问题.

这个题目的历史背景可参考百度百科, 这里把问题改得简单一点. 几个人围成一圈, 每隔一个人杀一个人, 求最后幸存者的编号.

设 \(J(n)\) 表示总人数为 \(n\) 最后活下来的编号. 如果 \(n\) 是偶数, 那么除了人数仅剩一半和编号不同之外前后的情景是一致的. 假设一开始有 \(2n\) 个人, 经过第一轮会剩下 \(1, 3, \dots ,2n-1\), 一个人对应的号码应该加倍然后减一, 也就是说 \(J(2n)=2J(n)-1\), 对于奇数的情形, 活下来的人是 \(1, 3, \dots , 2n+1\), 这一次他们的号码加倍并增加了一,故 \(J(2n+1)=2J(n)+1\). 于是我们得到递推式:

\[J(n)=\left\{ \begin{aligned} 1 && n=1 \\ 2J(\frac{n}{2})-1 && n=2k,k\in \mathbb Z \\ 2J(\lfloor\frac{n}{2}\rfloor)+1 && n=2k+1,k\in \mathbb Z \end{aligned} \right. \]

目前对于求出 \(J(n)\) 我们还没有什么头绪, 于是我们先打个表.

如图, 我们注意到 \(J(2^m+l)=2l+1\), 尝试证明这个结论. 我们对 \(m\) 使用数学归纳法. 当 \(m=0\) 时, \(J(1)=1\) 显然成立. 我们上面求递推式的过程启发我们对 \(l\) 分奇偶讨论. 当 \(l\) 为偶数, \(J(2^m+l)=2J(2^{m-1}+\frac{l}{2})-1=2\times( \frac{l}{2}+1)-1=2l-1\), 结论成立; 当 \(l\) 为奇数时类似的可以证明.

解决了问题后再发散思维联想联想, 发现我们的证明过程中离不开 2 的次幂, 考虑研究这之间的关系. 设 \(n=(b_mb_{m-1}b_{m-2}\dots b_{2}b_1b_0)_2\), 注意到 \(J(n)=(b_{m-1}b_{m-2}\dots b_2b_2b_0b_m)\), 也就是说 \(J(n)\) 把 \(n\) 向左循环移动了一位.

现在我们对 \(J(n)\) 已经有了一个透彻的认识，接下来考虑推广。我们试着求形如

\[f(n)=\left\{ \begin{aligned} 1 && n=\alpha \\ 2f(\frac{n}{2})+\beta && n=2k,k\in \mathbb Z \\ 2f(\lfloor\frac{n}{2}\rfloor)+\gamma && n=2k+1,k\in \mathbb Z \end{aligned} \right. \]

的递推式的封闭形式。打个表注意到 \(\alpha,\beta,\gamma\) 的系数存在一定规律，于是我们就能把 \(f(n)\) 对 \(\alpha,\beta,\gamma\) 的依存关系分开，表示为：

\[f(n)=A(n)\alpha+B(n)\beta+C(n)\gamma \]

注意到 \(A(n)=2^m，B(n)=2^m-1-l，C(n)=l\)，数学归纳法可证。

书中告诉我们，对付感性上“线性的”递推式，可以先带入一个特殊的式子。这种求递推式封闭形式的方法被称作成套方法。

练习题：

8

解递归式：

\[Q_0=\alpha,Q_1=\beta \]

\[Q_n=(1+Q_{n-1})/Q_{n-2} \]

sol

$$Q_2=\frac{1+\beta}{\alpha}$$

\[Q_3=\frac{\alpha+\beta+1}{\alpha\beta} \]

\[Q_4=\frac{\alpha+1}{\beta} \]

\[Q_5=\alpha,Q_6=\beta \]

于是这是个周期函数。

24

求所有形如

\[X_n=\frac{1+a_1X_{n-1}+a_2X_{n-2}+\dots+a_kX_{n-k}}{b_1X_{n-1}+b_2X_{n-2}+\dots+b_kX_{n-k}} \]

的递归关系，使无论 \(X_0,X_1,\dots,X_{k-1}\) 如何，它的解都是周期的。

sol

前面的第八题就是个满足条件的式子。本书还给了 $X_n=2i\sin \pi r+1/X_{n-1}$ 这一递推式。

第二章 和式

2.1 和式与递归式

和式和递归式可以转化。和式

\[S_n=\sum_{i=1}^n a_i \]

等价于递归式

\[S_n=S_{n-1}+a_n \]

也就是说，用第一章中求解封闭递归式的方式，我们就可以用封闭形式计算和式的值。反过来，递归式也可以通过转化为和式来求解。例如汉诺塔的递归式：

\[T_0=0 \\ \\ T_n=2T_{n-1}+1 \]

注意到，如果我们令 \(S_n=T_n/2^n\)，我们就有：

\[S_0=0 \\ \\ S_n=S_{n-1}+2^{-n} \]

由此得到 \(S_n=\sum_{k=1}^n 2^{-k}\)，进而可求出 \(T_n\)。

那我们是怎么注意到的呢？实际上对于任何形如

\[a_nT_n=b_nT_{n-1}+c_n \]

的递归式我们都可以用求和因子的思想把它转化成和式形式。具体地，我们让求和因子 \(s_n\) 乘在等式两边：

\[s_na_nT_n=s_nb_nT_{n-1}+c_ns_n \]

我们需要选取 \(s_n\) 使 \(s_nb_n=s_{n-1}a_{n-1}\)，这样设 \(S_n=s_na_nT_n\)，则

\[S_n=S_{n-1}+c_ns_n \]

于是

\[S_n=s_0a_0T_0+\sum_{i=1}^ns_ic_i\\T_n=\frac{1}{s_na_n}(s_1b_1T_0+\sum_{k=1}^ns_kc_k) \]

我们可以容易地求出来 \(s_n=\frac{\prod_{k=1}^{n-1} a_k}{\prod_{k=2}^n b_k}\)。于是傻子都可以注意到了。但我们必须注意分母时刻不能为0。

2.2 和式的处理

和式的处理在于简化或接近目标。

2.2.1 和式运算律

分配率：\(\sum\limits_{k\in K}ca_k=c\sum\limits_{k\in K}a_k\)

结合律：\(\sum\limits_{k\in K}(a_k+b_k)=\sum\limits_{k\in K}a_k+\sum\limits_{k \in K}b_k\)

交换律：\(\sum\limits_{k\in K}a_k=\sum\limits_{p(k)\in K}a_{p(k)}\)

小高斯算一到一百的和的过程相当于利用了和式的交换律。

2.2.2 扰动法

就是在求解和式的时候把单独一项从和式中分出去，重新改写式子然后运算。其思想从未知的和式 \(S_n=\sum_{0 \leq k \leq n}a_k\) 开始。然后通过他的最后一项和第一项分离出来，用两种方法改写 \(S_{n+1}\)：

\[S_n+a_{n+1}=\sum_{0 \leq k \leq n+1}a_k=a_0+\sum_{1 \leq k \leq n+1}a_k =a_0+\sum_{1 \leq k+1 \leq n+1}a_{k+1} =a_0+\sum_{0 \leq k \leq n} a_{k+1} \]

然后我们尝试用 \(S_n\) 表示最后那个和式，然后就得到方程，解就完了。

例：求一般的几何级数的和：

\[S_n=\sum_{0\leq k \leq n}ax_k \]

用一般的扰动法格式，得

\[S_n+ax^{n+1}=ax^0+\sum_{0\leq k\leq n}ax^{k+1} \]

由分配率得 \(RHS=ax^0+xS_n\)，于是 \(S_n+ax^{n+1}=a+xS_n\)，得到我们早就熟记的公式：

\[S_n=\frac{a-ax^{n+1}}{1-x} \]

2.3 多重和式

\[\sum_{j}\sum_{k}a_{j,k}[P(j,k)] \]

就是 \(\sum_{j}(\sum_{k}a_{j,k}[P(j,k)])\) 的缩写，在这样的情形，我们说此二重和式“首先关于 \(k\) 求和”。考虑改变求和的次序。我们有一个成为交换求和次序的基本法则，这推广了我们之前见过的结合律。

\[\sum_{j}\sum_{k}a_{j,k}[P(j,k)]=\sum_{P(j,k)}a_{j,k}=\sum_{k}\sum_{j}a_{j,k}[P(j,k)] \]

一个经典的二重和式简化问题是

\[\sum_{1\leq j,k\leq n}a_jb_k=\sum_{j,k}a_jb_k[1\leq j,k\leq n]=\sum_{j}\sum_{k}a_jb_k[1\leq j\leq n][1\leq k \leq n] \\ =\sum_{j}a_j[1\leq j \leq n](\sum_{k}b_k[1\leq k \leq n])=(\sum_{j}a_j[1\leq j\leq n])(\sum_{k}b_k[1\leq k \leq n]) \\= (\sum_{j=1}^na_j)(\sum_{j=1}^nb_k) \]

更一般的，我们可以得到

\[\sum_{j\in J}\sum_{k\in K}a_jb_k=(\sum_{j\in J}a_j)(\sum_{k\in K}b_k) \]

然后考虑如果 \(k\) 的取值与 \(j\) 有关系的情况下的交换求和次序法则，我们有

\[\sum_{j\in J}\sum_{k\in K(j)}a_{j,k}=\sum_{k\in K'}\sum_{j\in J'(k)}a_{j,k} \]

其中集合 \(J,K,J',K'\) 以以下方式关联：

\[[j\in J][k\in K(j)]=[k\in K'][j\in J'(k)] \]

常见的例子是 \([1\leq j\leq n][j\leq k\leq n]=[1\leq j\leq k\leq n]=[1\leq k\leq n][1\leq j\leq k]\)。

我们知道 \(\sum_{j\in J}a_j=\sum_{p(k)\in J}a_{p(k)}\)，那么如果有任意函数 \(f\)，

\[f:J\rightarrow K \]

将 \(j\in J\) 变成 \(f(j)\in K\)，那么用 \(f(j)\) 替换 \(k\) 会发生什么？考虑算贡献，有

\[\sum_{j\in J}a_{f(j)}=\sum_{k\in K}a_k\# f^{-}(k) \]

这里，\(f^{-}(k)\) 表示集合

\[f^{-}(k)=\{j|f(j)=k\} \]

2.4 一般性的方法

例子：求 \(\square_n=\sum_{k=0}^n k^2\)。

法 0：查表

查询 deepseek 我们得到

\[\square_n=\frac{n(n+1)(2n+1)}{6} \]

法 0.5：猜测答案，然后证明

这似乎比查表还难用，因为人类的注意力往往是有限的，而归纳法的证明是平凡的。

法 1：对和式用扰动法

\[\square_n + (n+1)^2 = \sum_{k=0}^{n}(k+1)^2 = \sum_{k=0}^n(k^2+2k+1) \\=\sum_{k=0}^n k^2 + 2\sum_{k=0}^n k +n \\=\square_n+2\sum_{k=0}^n k+n \]

丸辣，\(\square_n\) 被抵消了！但我们发现这样可以推出 \(\sum_{k=0}^n k\)！

于是我们考虑通过扰动 \(f(n)=\sum_{k=0}^n k^3\) 来求 \(\square_n\)。

\[f(n)+(n+1)^3=\sum_{1\leq k\leq n}(k+1)^3=\sum_{1\leq k\leq n}(k^3+3k^2+3k+1)=f(n)+3\square_{n}+3\frac{(n+1)n}{2}+(n+1) \]

然后就得到我们利用法 0 得到的结果。

法 2：建立成套方法

我们知道求解递归式的成套方法。递归式

\[R_0=\alpha\\ R_{n}=F_{n-1}+\beta+\gamma n+\delta n^2 \]

的解的一般形式为

\[R_n=A(n)\alpha+B(n)\beta+C(n)\gamma+D(n)\delta \]

\(\delta=0\) 时的情况我们已经见过，这样就确定了 \(A(n),B(n),C(n)\)。

我们将 \(R_n=n^3\) 带入，得到此时 \(\alpha=0,\beta=1,\gamma=-3,\delta=3\)，于是

\[3D(n)-3C(n)+B(n)=n^3 \]

这就确定了 \(D(n)\)。

如果在上面的式子中令 \(\alpha=\beta=\gamma=0,\delta=1\)，那么就得到 \(\square_n=R_n=D(n)\)，就出来了。

法 3：欲擒故纵

我们用一个看似更难的二重和式来代替这个合适，只要拿捏得当，我们就可以得到一个很优雅的证明过程。

\[\square_n=\sum_{k=1}^n k^2=\sum_{1\leq j\leq k\leq n}k=\sum_{j=1}^n\sum_{k=j}^nk=\sum_{1\leq j\leq n}(\frac{j+n}{2})(n-j+1) \]

然后得到了一个 \(\square_n\) 的方程，然后就得到了结果。

法 4：有限微积分

见章节 2.5 中的讲解。

法 5：生成函数

2.5 有限微积分和无限微积分

无限微积分基于由

\[{\rm D}f(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \]

所定义的微分算子 \(\rm D\) 的性质。有限微积分则基于由

\[\Delta f(x)=f(x+1)-f(x) \]

所定义的差分算子 \(\Delta\) 的性质。这两个东西被称为算子，是因为他们作用在函数上给出了新的函数，用于产生新的函数。

早先我们学习微积分的时候我们知道 \(D(x^m)=mx^{m-1}\)，我们希望 \(\Delta\) 也能有类似的优雅结论，可惜

\[\Delta(x^3)=(x+1)^3-x^3=3x^3+3x+1 \]

但是对于下降阶乘幂 \(x^{\underline{m}}=x(x-1)\dots(x-m+1)\)，整数 \(m\geq 0\) 来说，我们有

\[\Delta(x^{\underline{m}})=mx^{\underline{m-1}} \]

与之对应的，我们定义上升阶乘幂 \(x^{\overline{m}}=x(x+1)\dots(x+m-1)\)，整数 \(m\geq 0\)。

我们知道无限微积分的算子 \(\rm D\) 有一个逆运算即逆积分算子（或者说积分算子）\(\int\)。微积分基本定理把 \(\rm D\) 和 \(\int\) 联系起来：

\[g(x)={\rm D}f(x)\iff \int g(x){\rm d}x=f(x)+C \]

类似的，\(\Delta\) 也有一个逆运算，即逆差分算子（或者说求和算子）\(\sum\)，而且有一个类似的基本定理

\[g(x)=\Delta f(x)\iff \sum g(x)\delta x=f(x)+C \]

这里 \(\sum g(x)\delta x\) 是 \(g(x)\) 的不定和式。

我们知道无限微积分有定积分：如果 \(g(x)={\rm D}f(x)\)，那么

\[\int_{a}^bg(x){\rm d}x=f(x)\mid_{a}^b=f(b)-f(a) \]

于是，有限微积分——一直在模仿其更出名的同类——也有“定和式”：如果 \(g(x)=\Delta f(x)\)，那么

\[\sum_{a}^bg(x)\delta x=f(x)\mid_{a}^b=f(b)-f(a) \]

容易发现 \(\sum_{a}^bg(x)\delta x=\sum_{a\leq k<b}g(k)\)。

通过吧 \(g(x)\) 展开为 \(f(k+1)-f(k)\)，我们可以得到被我们称为叠缩的和式

\[\sum_{a\leq k < b}(f(k+1)-f(k)) \]

对于负指数的下降幂的一般定义是

\[x^{\underline{-m}}=\frac{1}{(x+1)(x+2)\dots(x+m)},m>0 \]

我们有性质 \(x^{\underline{m+n}}=x^{\underline{m}}(x-m)^{\underline{n}}\)。

可惜的是 \(\Delta(f(g(x)))\) 确实没有什么优雅的性质，但是 \(\Delta(f(x)g(x))\) 有一个很好的性质。

回顾一下无限微积分里面的相似的东西，我们有

\[{\rm D}(uv)=u{\rm D}v+v{\rm D}u \]

两边积起来就有分部积分法

\[\int u{\rm D}v=uv-\int v{\rm D}u \]

然后考虑有限微积分。

\[\Delta(u(x)v(x))=u(x+1)v(x+1)-u(x)v(x+1)+u(x)v(x+1)-u(x)v(x)=u(x)\Delta v(x)+v(x+1)\Delta u(x) \]

我们利用由

\[{\rm E}f(x)=f(x+1) \]

定义的移位算子表示成方便的形式

\[\Delta(uv)=u\Delta v+{\rm E}v\Delta u \]

两边同时做有限微积分，得到分部求和法

\[\sum u\Delta v=uv-\sum{\rm E}v\Delta u \]

2.6 无限和式

\[\sum_{k\geq 0}a_k=\lim_{n\rightarrow \infty}\sum_{k=1}^na_k \]

经过两个或多个指标集的绝对收敛的和式永远可以对这些指标中的任何一个首先求和。我说完了。

第三章 整值函数

3.1 底和顶

对于所有实数 \(x\)，定义底函数和顶函数

\[\lfloor x\rfloor=小于等于 x 的最大整数 \]

\[\lceil x\rceil=大于等于 x 的最小整数 \]

两者的图像如下，红色的是 \(y=\lfloor x\rfloor\)，蓝色的是 \(y=\lceil x \rceil\)。

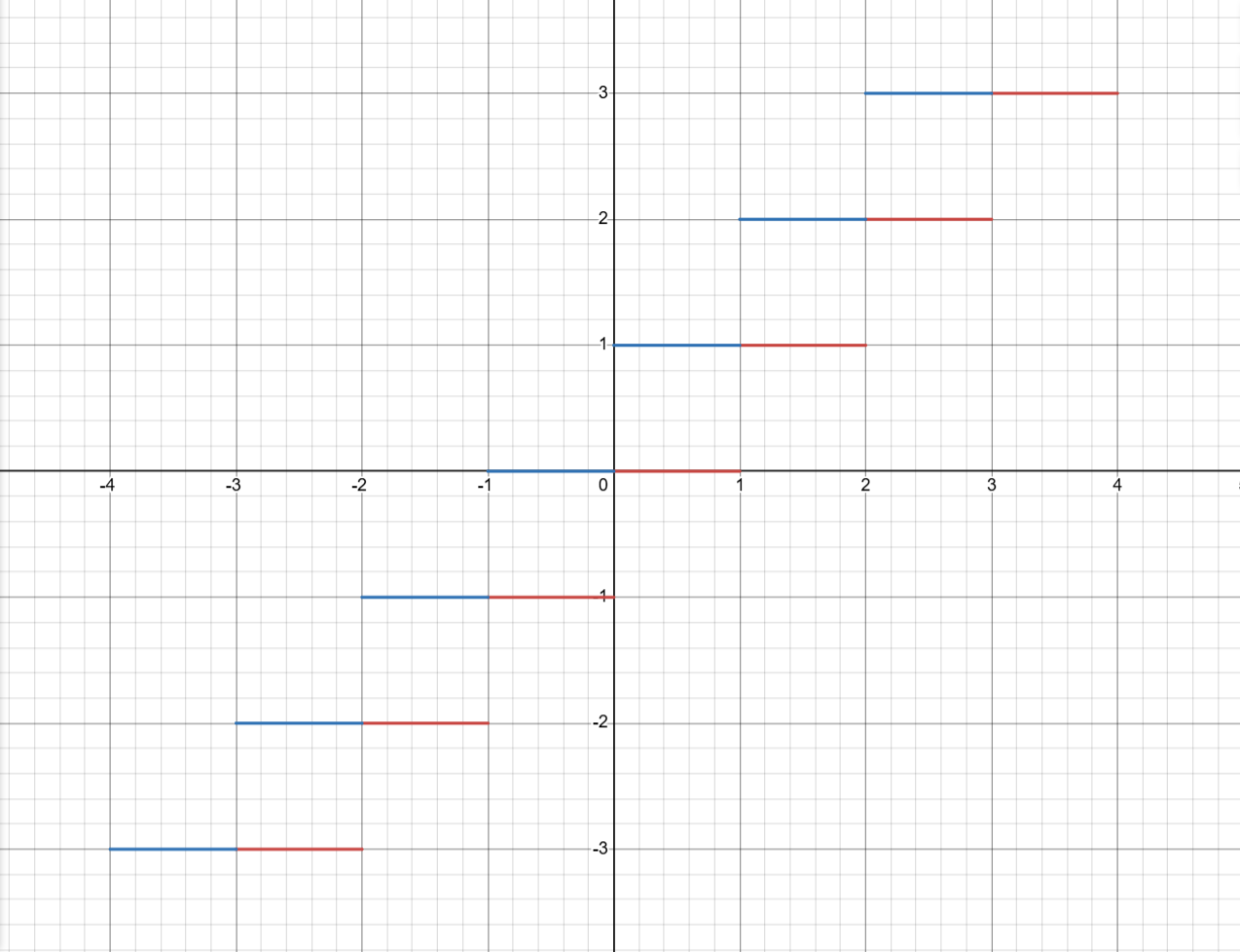
容易知道

\[\lfloor x\rfloor = x\iff x 是整数\iff \lceil x\rceil = x \]

而当它们不相等的时候，顶函数恰好比底函数大 1：

\[\lceil x\rceil -\lfloor x\rfloor=[x 不是整数] \]

观察图像可知这两个函数关于两个坐标轴互为反射：

\[\lfloor-x\rfloor=-\lceil x\rceil;\lceil-x\rceil=-\lfloor x\rfloor \]

我们希望一些不依赖于图形的法则，于是有

\[\lfloor x\rfloor=n\iff n\leq x<n+1,(a) \\ \lfloor x\rfloor=n\iff x-1<n\leq x,(b) \\ \lceil x\rceil=n\iff n-1<x\leq n,(c) \\ \lceil x\rceil=n\iff x\leq n<x+1,(d) \]