BUUCTF rsa2
首先打开题目

既然已知n和e,那么使用factordb分解n得到p和q

然后根据自己在网上找到的脚本计算d
import gmpy2 from Crypto.Util import number p = 11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937 q = 9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183 e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085 d = gmpy2.invert(e,(p-1)*(q-1)) print (d)

接着将得到的d带入题目计算

发现报错,由于自身代码能力有限,去网上找大佬脚本
1 import gmpy2 2 import hashlib 3 4 def transform(x, y): # 使用辗转相处将分数 x/y 转为连分数的形式 5 res = [] 6 while y: 7 res.append(x // y) 8 x, y = y, x % y 9 return res 10 11 12 def continued_fraction(sub_res): 13 numerator, denominator = 1, 0 14 for i in sub_res[::-1]: # 从sublist的后面往前循环 15 denominator, numerator = numerator, i * numerator + denominator 16 return denominator, numerator # 得到渐进分数的分母和分子,并返回 17 18 19 # 求解每个渐进分数 20 def sub_fraction(x, y): 21 res = transform(x, y) 22 res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res))))) # 将连分数的结果逐一截取以求渐进分数 23 return res 24 25 26 def get_pq(a, b, c): # 由p+q和pq的值通过维达定理来求解p和q 27 par = gmpy2.isqrt(b * b - 4 * a * c) # 由上述可得,开根号一定是整数,因为有解 28 x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a) 29 return x1, x2 30 31 32 def wienerAttack(e, n): 33 for (d, k) in sub_fraction(e, n): # 用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数 34 if k == 0: # 可能会出现连分数的第一个为0的情况,排除 35 continue 36 if (e * d - 1) % k != 0: # ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n) 37 continue 38 39 phi = (e * d - 1) // k # 这个结果就是 φ(n) 40 px, qy = get_pq(1, n - phi + 1, n) 41 if px * qy == n: 42 p, q = abs(int(px)), abs(int(qy)) # 可能会得到两个负数,负负得正未尝不会出现 43 d = gmpy2.invert(e, (p - 1) * (q - 1)) # 求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元d 44 return d 45 print("该方法不适用") 46 47 48 n = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471 49 e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085 50 d = wienerAttack(e, n) 51 print("d=", d) 52 k = hex(d)[2:] 53 flag = "flag{" + hashlib.md5(k.encode('utf-8')).hexdigest() + "}" 54 print(flag)
得到flag{a8eb82576211d716e354586aad3b099d},没想到这里提交失败,后来才知道要用python2运行
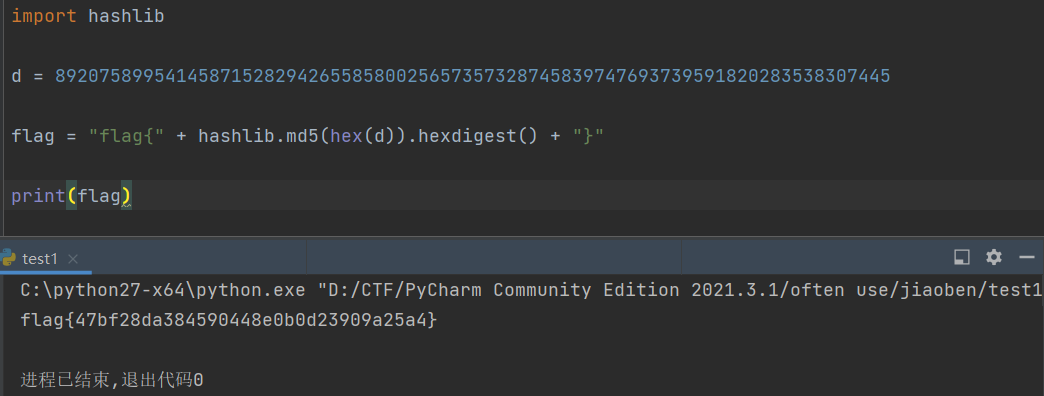
得到flag




 浙公网安备 33010602011771号
浙公网安备 33010602011771号