题

当需要取模的程序中有减法时，需要将答案加上模数再模一下
例如:

ans = pow(2, n) % mod;
ans -= (n + 1);
ans = (ans + mod) % mod;

P3723

给定两个长度为n的序列，可以平移(例如，a={1,2,3,4}, 平移后a={2,3,4,1}),也可以给任意一个区间的所有数加上一个非负整数，求操作后的$\sum_{i=1}^{n}(x_i - y_i)^2 $最小
问题很容易就转化成了求

\[\sum_{i=1}^{n}(x_i- y_{i+k}+c) \]

\[=\sum_{i=1}^{n}(x_i^2+y_i^2)+2c\sum_{i=1}^{n}(x_i-y_i)+nc^2-2\sum_{i=1}^{n}(x_iy_i) \]

不难发现，如果要求最小值的话，要求第3，4项更小，最后一项更大
又不难发现，当$x,y,c,n$给定时，前三项是确定的，只需要求最后一项即可
然后这里有个发现，最后一项的$x,y$的角标的差值相同，而卷积的角标的和相同，而卷积又可以用fft优化到$O(n\log n)$所以想办法转成卷积

设$y'_i = y_{n-i}$原式变为
$\sum_{i=1}^{n}(x_iy'_{n-i}) $差值就相同了
剩下用fft优化即可\

注意：$\sum_{i=1}^{n}(x_i-y_{i + k}+c)^2$，这个式子里，给x加时，c>0,给y加时，c<0，代码中c不能从0开始枚举

CF741D

dsu on tree 的题和CF600E大同小异
这里给出一个会出错的写法：

void solve(int u, int fa, int Dep) {
    for(int i = 0; i < 22; i ++) {
        int k = (1 << i);
        max_len = max(max_len, dep[u] + t[k ^ Xor[u]] - 2 * Dep);
    }
    max_len = max(max_len, dep[u] + t[Xor[u]] - 2 * Dep);
    for(int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa) continue;
        solve(v, u, Dep);
    }
}

上述代码是实现统计子树里的答案时的操作，问题出在哪呢？
当$t[k \oplus Xor[u]] == 0 || t[Xor[u]] == 0$时，即子树内没有异或出来是这个值的，那么用这个值更新就是错误的
正确的写法应该加上特判：

void solve(int u, int fa, int Dep) {
    for(int i = 0; i < 22; i ++) {
        int k = (1 << i);
        if(!t[k ^ Xor[u]]) continue;// 如果他是0，那么不可用他的值更新
        max_len = max(max_len, dep[u] + t[k ^ Xor[u]] - 2 * Dep);
    }
    if(t[Xor[u]]) max_len = max(max_len, dep[u] + t[Xor[u]] - 2 * Dep);// 如果他是0，那么不可用他的值更新
    for(int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa) continue;
        solve(v, u, Dep);
    }
}

西安集训3.26 t2

找出所有有可能产生贡献的边，这个边一定是左右两边的$size\ge k$,然后找出s条这样的边，(从根开始连续的，因为这样好构造出来)。

注意：

如果要把以$u$为根的子树染上$1$_{$k$,并且要求这颗子树不能产生贡献的时候，应该把根节点染成$1$，儿子节点染成$2$}$k$，这样就不会让这棵树产生贡献了
如果选出来的边是从根开始的一条链，那么，应让根节点为$1$，没被选上的边的另一个端点的子树染成$2$~$k$，与上一个同理

~~这个思路真的太天才了~~
把行和列分成两边，给了一个$x,y$就连$x\leftrightarrow y$，连完了发现，最后，可以生成所有元素的时候，整张图就会变成一个大连通块，那么问题就转换成了用最少的边把现在的图连成一个连通块，那很显然就是目前连通块的数量减$1$(两个连通块之间连一条边，就会使这两个连通块变成一个连通块，合并一个再合并一个，那么就是目前连通块的数量减$1$)

P3386

KM算法，核心思想就是对于每一个点，遍历每一条出边(其出点称为$v$)，如果能直接匹配就匹配，不能就让匹配$v$的点尝试选择另外的点，递归下去即可，如果能够选到其他的点，那么就让这个点选其他的点就好了，此时最大匹配数会加$1$，(证明详见增广路算法)(代码详见code)

坑点

这样写：

void solve() {
    for(int u = 1; u <= n; u ++) {
        for(int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            if((match[v] == 0) || (dfs(match[v], ++ cnt))) {
                ans ++;
                match[v] = u;
                break;
            }
        }
    }
}

会T

void solve() {
    for(int u = 1; u <= n; u ++) {
        if(dfs(u, ++ cnt)) {
            ans ++;
        }
    }
}

这么写，不会T
但是感觉是一样的o(TヘTo)

P4822

建分层图跑最短路即可。

注意：建分层图的时候先建出k层，再在k层之间连边

一下写法是不对的(也可能是我写的太丑)

for(int k = 1; k <= K; k ++) {
    for(int u = 1; u <= n; u ++) {
        for(int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to, w = edge[i].w;
            w /= 2;
            int ru = u + (k - 1) * n;
            v = v + k * n;
            edge[++ tot] = {v, head[ru], w};
            head[ru] = tot;
            ru += n;
            w *= 2;
            edge[++ tot] = {v, head[ru], w};
            head[ru] = tot;
        }
    }
}

问题是出现在第二层循环，是b按照第一层的边连其他层的边，但是在处理完第一层与第二层后的连边后处理第三层的时候会多建边(因为第一层这个模板边多了)

dij不能解决有负边的最短路！！！！！！！！

P5410拓展KMP/Z函数

注意的点

如果现在枚举出的答案刚好等于$r-i+1$那么还是需要继续暴力枚举，因为后面是不确定能不能匹配上的

int x = i - l + 1;
int rr = r - l + 1;
int len = z[x];
if(i + len - 1 < r) {
    z[i] = len;
}

$if$里的是对的
2. 暴力枚举的时候要判断一下$i+len-1<=m$

P8600连号区间数

当$max-min-r+l=0$时，这个区间是连号区间
当固定一个右端点$r$的时候，问题就转化成了$1$~$r$中有多少$l$满足第$1$条性质
单调栈可以维护后缀$max$或后缀$min$,例如，一个递增的单调栈:$\{(2,2),(4,3)\}$(右端点为$3$)(第一个元素代表值，第二个元素代表其在原数组里的下标)中$(2,2)$代表的就是$1$~$2$的后缀$min$为$2$
可以用线段树维护以$r$为右端点，$1$~$r$中满足第一条性质的个数
由于$max-min-r+l>0$所以$4$可以改为维护最小值及个数

做法:先固定一个$r$，用线段树维护$max-min-r+l$的最小值和个数,其中叶子节点表示的是这个节点所代表的$l$到$r$的$max-min-r+l$;用单调栈维护后缀$max$和$min$，当$r$向右拓展就弹栈，同时更改线段树维护的$max-min-r+l$;最后查询$1$~$r$的最小值及个数，如果最小值等于0就把个数贡献到最终的答案里面。

6.25

sez682

题目:
$L=g^y \mod p,R=g^x\mod p, 求M=g^{xy}\mod p(x,y取最小值)$

$g^{xy}\neq g^x\cdot g^y$
$map$的$clear$操作时间复杂度$O(n)$
直接利用$BSGS$算法将$y$和$x$求出算最后答案,但实际上只需要求出$x$ 或 $y$就行，因为$M=L^x\mod p=R^y\mod p$可以省时间(BSGS传送门)

6.26

P6748

因为只关注一条边的边权是否大于两端端点的点权，于是可以设答案数组为$f$
设$f_{u,0}:$当$val(fa(u), u)\le a_u $时以点$u$为根的子树的最大边权权值和,\ 设$f_{u,1}:$当$val(fa(u), u)> a_u $时以点$u$为根的子树的最大边权权值和;\ 最终只需要输出$f_{rt,1}$即可; 这时发现是一个树形dp，考虑如何转移。如果当前在$u$,其儿子的答案已经都求出，此时需要找一些边让他的$val>a_u$，所以还需要维护另一个数组$g$
$g$定义：
$g_{u,0}:当val(fa(u), u)\le a_{fa(u)}$时以点$u$为根的子树加上$val(fa(u), u)$的最大边权权值和,
$g_{u,1}:当val(fa(u), u)> a_{fa(u)}$时以点$u$为根的子树加上$val(fa(u), u)$的最大边权权值和;
此时就可以用$u$儿子的$g$更新$f$了，然后再用$u$的$f$更新$u$的$g$了。

$g$更新$f$

设要选出$k$条边使$val(u,v)>a_u(v\in son(u))$
先选出所有的$g_{v,0} $,找出前$k$大$g_{v,1}-g_{v,0}(g_{v,1}-g_{v,0}>0)$贪心选出即可

$f$更新$g$

分论讨论:(找出不同的选择取$\max$即可)

$a_u\le a_{fa(u)} \dots$
$a_u> a_{fa(u)}\dots$

注意：

把$g_{v,1}-g_{v,0}$塞到数组里的时候要考虑不同层之间会不会有覆盖

P5495

前置知识：高维前缀和，欧拉筛，埃式筛

题目简介:
给定一个$a$数组，求$b$数组，$b$数组的求法为：

\[b_k=\sum_{i|k}a_i \]

所以$i$是$k$的约数，也就是说将$k$和$i$质因数分解后，$k$的每一个质数的次数$\ge$ $i$的每一个质数的次数。所以可以看作高维前缀和，质数个数就是维数。
得知这个结论后就可以做了。

做法：

筛出$1$~$n$之间的质数。
先枚举质数$phi_j$，把它当作维数，在这一维做前缀和，就是$a_{i\cdot phi_j}+=a_i$
最后求出$a$的异或和

注意：

因为模数为$2^{32}$，所以可以直接开unsigned int自然溢出就行
在做法的第2步不能先枚举$i$在枚举$phi_j$。(待证)

6.27

sez684

前置知识:高维前缀和，分解质因数，随机化

题目简介: 给定一个长度为$n$的$w$序列，要求找到一个长度至少为$\lfloor \frac{n}{2}\rfloor$的子序列使得其所有元素$\gcd$的值最大
数据范围: $2\le n\le 10^5,1\le w_i\le 10^{12}$
这样的题目不难想到先枚举$\gcd$，再判断是否合法，假定我们钦定一个数$d$为$\gcd$，那么可以发现$d$和发的时候当且仅当下面的式子成立

\[\sum_{i=1}^{n}[d|a_i]\ge\lfloor \frac{n}{2}\rfloor \]

解题思路及方法

利用概率的知识，当钦定一个$a_i$在答案中时，求出正确答案的概率大约为$\frac{1}{2}$,那么我们多找几个(设为$k$个)$a_i$取他们之中答案的最大值，求出正确答案的概率就大约为$1-\frac{1}{2^k}$，正确率就大大提高了
上面的式子看起来很像是高维后缀和 (以$a_1,\dots\ a_n$质因数分解后的质因子数作为维度，质因子的次数作为坐标，那么就可以抽象出一个高维空间，又因为$d|a_i$，所以满足条件的$a_i$每一个质因子的次数都$\ge d$的质因子次数)，但是高维后缀和的时间复杂度为$O(v\cdot 维度)(v为值域)$，而这里值域为$10^{12}$，所以很显然会炸，需要优化。
回想高维后缀和的过程，会发现有一些位置是不被需要的，也就是非$d$的倍数的位置，那么就要舍弃这些值，具体的做法就是只在钦定的$a_i$的因子中做高维后缀和，这样既能保证$d$的倍数能够全部枚举到，也能保证时间复杂度的正确性。
问题又来了，如果只在$a_i$的因子中做高维后缀和，那么比$a_i$大的值就没有办法产生贡献(直观一点的说就是在高维空间中比$a_i$大的值就没有位置了)。所以要考虑在保证正确性的情况下缩小$a$的值。不难发现，$a_j$能产生贡献只有当$d|a_j$时，又因为$d|a_i$，所以$d|\gcd(a_i, a_j)$,那么我们就可以把 $a_j$缩小为$\gcd(a_i, a_j)$了

问题基本解决

code

P1220

$0\le n\le 50$
题目已经说了贪心不行，所以要考虑dp

方法1：

想了好久的状态： $f_{t,l,r,0/1}$,含义为当时间为$t$的时候已经处理了$l,r$区间并且在左右两侧 (0代表左侧，1代表右侧)的最小值
转移： 考虑如何转移到$f_{r,l,r,0}$,可以从$l+1$走过去，也可以从$r$走过去，花费的时间是路程。$f_{t,l,r,1}$同理
转移方程

\[f_{t,l,r,0} = min(f_{t-w_{l+1}+w_l,l+1,r,0},f_{t-w_r+w_l,l+1,r,1})+t*p_l \]

\[f_{t,l,r,1} = min(f_{t-w_{r}+w_{r-1},l,r-1,1}, f_{t-w_r+w_l,l,r-1,0})+t*p_r \]

这道题就没了。注意看数组是否越界。

code

方法2：（题解）

方法一的时间复杂度大约是$O(n^3)$，虽然可以过，但是也难以接受，题解与方法一差不多，优化了转移的过程
状态 $f_{l,r,0/1} $,处理完$l,r$区间后总花费的最小值。 **注意**方法一的转移是处理$l,r$区间所需要的最小值，而方法二是处理完$l,r$区间后的所有路灯花费的最小值，所以还需要维护一个 $sum$数组来记录所有路灯的功率前缀和，方便转移
转移和方法一差不多，具体如下

\[f_{l,r,0}=min(f_{l+1,r,0}+(w_{l+1}-w_l)*(sum_n-sum_r+sum_l),\\ f_{l+1,r,1}+(w_r-w_l)*(sum_n-sum_r+sum_l)) \]

\[f_{l,r,1}=min(f_{l,r-1,1}+(w_r-w_{r-1})*(sum_n-sum_{r-1}+sum_{l-1}),\\ f_{l,r-1,0}+(w_r-w_l)*(sum_n-sum_{r-1}+sum_{l-1})) \]

code

P2466

和关路灯 基本一样，不过加强了数据，能发现如果想要求最后的最大值，可以转化成求浪费的最小值
这样不难发现，如果将速度$v$看作功率，将路程看作时间，那么这道题就完全转化成了关路灯了
更具体的，设一个$dp$数组$f$
设$f_{l,r,0/1}$为处理完$l,r$区间内的彩蛋后浪费的最小值，(0表示在目前在左侧，1表示目前在右侧)，可得状态转移方程如关路灯，(此时$1\le n\le 1000$,必须用$O(n^2)$的做法)，然后就没了

注意：

因为题目没有保证$x$为单调递增，所以首先需要排序，排完序后才能够进行操作和求 $sum$数组
如果把$l,r$看作是平面直角坐标系的下标的话，他们的值域是$-10^4$~$10^4$，会炸，所以$l,r$应是数组的下标，但是题目给的$x_0$代表的是平面直角坐标系的坐标，所以需要找到临近$x_0$的位置进行$dp$，还要将从$x_0$到这个临近位置的花费记入总答案里

code

P10814

题目简介 给定一个长为$n$的序列$a$,有$m$次询问，每次询问给定$l,r,x$,求$[l,r]$区间中小于等于$x$的元素个数。
数据范围 $1\le n,m,a_i,x,l,r\le 2\times10^6$ 时限$3$秒

思路：

首先看的这个要求小于等于$x$的元素个数可以想到权值线段树
看到这个区间查询能想到可持久化线段树，不过我们深思一下可以发现这个不用可持久化线段树也可以做，因为要求的是元素个数，所以其实可以想到前缀和，要求$[l,r]$区间的个数，只需要求出$[1,r]-[1,l-1] $即可
因为有多组询问，如果在线处理的时间复杂度是 $O(mn\log n)$，不能接受，所以考虑离线下来，因为只关注从$1$开始的区间的元素个数，所以可以把$l,r$分开处理，用边加边查的方法分别求出$l,r$的答案最终合并即可

注意：

因为线段树常数大，所以这道题用线段树会$T$，又因为只需要查询从$1$开始的区间，所以可以使用常数更小的树状数组。

code

补充：

题目名称叫做二维数点的原因如下：
将$(i, a_i)$ 抽象为平面直角坐标系中的一个点，我们的到一个询问$[l,r,x]$就可以分别求 $(1,1),(r,x),(r,1),(x,1)$四点围成的矩形内部的点（含边界）的个数减去$((1,1),(l,x),(l,1),(x,1))$四点围成的矩形内部的点（含边界），那么问题就转化成了二维数点了。

6.28

P6477 子序列问题

题目简介 给定一个正整数序列$A_1, A_2,\dots,A_n$, 设函数$f(l,r)$为$A_l,A_{l+1},\dots,A_n $中不同整数的个数，要求$\sum_{l=1}^{{n}\sum_{r=l}}(f(l,r))^2 $
数据范围 $1\le n\le 10^6,1\le A_i\le 10^9$

思路:

~~不难发现暴力不能过~~，根据数据范围，大概可以猜到这道题需要$O(n\log n)$的时间复杂度，不是二分就是线段树。
再次观察这个式子，因为是求和，所以可以把枚举顺序反转，变成$\sum_{r=1}^{{n}\sum_{l=1}}(f(l,r))^2 $,如果设$g(r)=\sum_{l=1}^{r}(f(l,r))2$,那么就得出$\sum_{r=1}^{n}g(r) $,只要能够在$\log n$的时间复杂度内求出$g(r)$就行
假设我们现在要求的位置是 $r$，不难发现，如果$A_r$上次出现的位置是$l$，那么$[1,l]$到$r$的$f$函数的值没变，也就是不同整数个数没变，这一部分可以继承$g(r-1)$的，但是$g$函数不能够拆解，所以要考虑怎么把剩下的部分也用$g(r-1)$更新。
能发现剩下的部分所有的$f$函数都加了$1$,利用完全平方公式可得$(f+1)^2=f2+2f+1 $，可以看到$f^2$就是$g(r-1)$的部分，所以也可以直接继承过来，在单独求剩下的$2f+1$。
观察$2f+1$，发现可以分开求，$2f$可以直接求一个区间和（所以要用到线段树），$1$就是区间的长度，

总结一下，我们需要一个$g$数组，还需要一个线段树维护$f$函数的值，需要支持的操作有区间和，区间加，然后这道题就没了

注意：

如果用动态开点线段树，在懒标记下放的过程中遇到没有开的点需要在开一个，否则就死了

P7124 stcm

首道黑啊太不容易了
题目简介 给定一棵树，需要一个集合，有三种操作

在集合中插入一个节点$x$
撤回上一次插入操作
将当前点集标为第$i$个节点的子树补信息
一个点$x$的子树补信息定义为，书的点集出去$x$的子树(包括$x$)内的点得到的集合；需要保证每个点的子树补信息都是正确的。

数据范围 $1\le n\le 10^5$。

题目思路

如果把这棵树用$dfs$序转成一个区间序列，使得节点$x$及其子树的$dfn$编号是连续的，能发现，不同节点在区间上的范围不是包含就是不交，有了这个性质以后，又能发现，包含一个点的区间按照$l$排完序后，$r$也就是单调的了，这样就可以一直加点直到处理完了。
但是如果暴力枚举这个点的话，实现的复杂度是$O(n^2)$的，肯定是不能的，此时就考虑分治，假设现在要处理$[l,r]$区间且$[1,l-1],[r+1,n]$都被加入了集合，那么枚举一个区间$mid$，把包含这个点的区间处理完，把不包含这个点的区间分别放到左右两边递归进行处理。
每一层递归的时间复杂的是 $O(n)$，所以总复杂度就是$O(n\log n)$

注意：

在思路2中，处理完 $mid$后，要把$l,r$恢复到原来位置，再递归操作。且需要维护一个
vector，记录在$[l,r]$之内的区间，如果暴力枚举会$T$
删点的时候需要判断现在处理了几个，如果处理完了直接返回就不用再删点了。

6.29

P3804 【模板】后缀自动机（SAM）

题目简介 给定一个只包含小写字母的字符串$S$，求出$S$的所有出现次数大于$1$的子串的出现次数乘上该子串的最大值。
直接说结论：用后缀自动机SAM解决

后缀自动机SAM

6.30

P4070 [SDOI2016] 生成魔咒

题目简介 $S$一开始是空串，共进行$n$次操作，每次向$S$中插入一个字符，每次操作完需要输出$S$中的本质不同子串数量
看到子串数量就知道用SAM解决了。
就是计算$len(p)-len(link(p))$的和,就没了，板子题

注意：

$SAM$的空间复杂度是$2n-1$,所以要开够空间

P3809 【模板】后缀排序

题目简介 给定一个字符串，将所有后缀从小到大排序，然后按照顺序输出后缀第一个字符在原串中的位置。位置编号为$1$到$n$。
思路及方法 把上述题意转化一下就成了求出原串的$sa$数组，就成了后缀数组的板子题了

注意：

求后缀数组的时候长度是倍增加的，每次长度会$\times$ 2，如果不这么写复杂度就会变成$O(n^2)$,显然是假的，实际正确的复杂度应该是$O(n\log n)$

SP10570 LONGCS - Longest Common Substring

题目简介 给出不同字符串，求所有字符串的最长公共子串的长度。
瞪出来的性质：

首先公共子串长度满足单调性，所以可以二分
一个子串是原字符串的一个后缀的一个前缀，这就让人联想到了$SA$中的$height$

做法：

把所有字符串拼在一起，(字符串之间需要有间隔符，否则会$WA$)然后找出$SA$，求出后缀数组和$height$数组，
二分出一个$mid$，利用双指针在排完序的后缀的$height$数组上找一段连续的区间，要求这段区间的$height\ge mid$，并且$[i,i+mid-1]$（$i$为后缀编号）同属一个字符串

code

注意：

数组绕来绕去有点绕，容易写错，要在脑子清楚的时间写
二分一定要注意边界，否则容易死循环
检查$SA$有没有写错

7.1

SP1812 LCS2 - Longest Common Substring II

是上面那道题的经验，可以用这个在巩固一下$SA, height,$二分

SP7258 SUBLEX - Lexicographical Substring Search

题目简介 给定一个字符串，多次询问求本质不同排名第$k$小的子串。
思路：

子串是一个后缀的前缀，所以可以用$SA$和$height$解决
因为$SA$是按照字典序排序，所以排名为$i$的后缀的任意一个前缀都比排名为$i+1$的任意一个前缀要小
假设两个排名$k_1,k_2(k_1< k_2)$，这样他们两个所代表的子串$i_1,i_2$（$i$为子串的第一个字符在原串的位置）得关系有且只有两种，情况一：后缀$i_1$比后缀$i_2$小，情况二：子串$i_1$是子串$i_2$的前缀

方法：

将所有询问离线，按照$k$排序
将后缀排序，求出$height$数组
设一个$K,p$，$K$表示已经处理了$K$个排名，$p$表示已经遍历到了排名为$p$的后缀
接受一个询问时，先把$k-K$，然后从$p$开始遍历后缀
按从小到大的顺序遍历后缀，判断该后缀的前缀个数是否大于$k$，（注意因为是本质不同的子串，所以前缀个数应该减去$height$）
情况一：$>k$，把$k$减去个数，然后继续向后遍历
情况二：$\le k$，记录下答案，排名为$k$的子串就是 $s[sa[i],sa[i]+height[i]+k-1]$
求出他的答案后，更新$K,p$

注意：

$K$要记录排名为$p-1$后缀在所有子串中的排名

code

P5341 [TJOI2019] 甲苯先生和大中锋的字符串

题目简介 找出一个字符串中恰好出现$k$次的子串的长度，并找出这些长度出现次数最多的长度，如果出现次数相同，输出更大的长度
思路因为后缀自动机能支持查找所有的子串，且一个状态$v$的$endpos$集合大小，也就是$parent$树上$v$子树内前缀节点个数就是这个状态所代表的字符串出现的次数，所以可以考虑建出$SAM$
做法

建出$parent$树，求出每一个状态点的子树的前缀节点的个数($设为val$)
如果$val_v=k$，就将$[len(fa_v)+1,len(v)]$区间内的长度的个数都加一，最终找出长度出现次数最多的长度

小优化：

在做法的第$2$步时，能发现需要把每一个区间都加一，但是我们只关注最后的数组，所以可以利用差分，做到$O(1)$修改$O(n)$查询（不差分暴力就会变成$O(n^2)$,用线段树会变成$O(n\log n)$）

7.3

sez662

题意：给定一个有向图，每次操作可以选择一个点，将它与他能到达的点全部删掉，问期望多少次能删完，答案对$998244353$取模。
首先得了解期望

我们定义随机变量$X$为删完所有的点所需要的操作次数，那么就可以得到

\[E[X]=\sum_xxP(x) \]

其中$x$表示一个事件操作的次数，也就是收益
那么把收益拆成一个一个的 $1$，也就相当于一个一个的点(可以理解为这个事件中操作了这些点)，然后把$P(x)$乘进去，然后就得到了

\[E[X]=\sum_xP(x)+P(x)+P(x)+P(x)+\cdots \]

设这次事件中操作的点为$a_i$，那么就可以把上面的式子看作是$a_i$在发生这次事件而被操作的概率之和。
考虑单个的点，其在所有事件中操作的概率之和就是其被操作的概率，那么问题就转化成了求所有点被操作的概率之和

考虑如何求一个点$i$被操作的概率：我们把能到达一个点的所有点(包括他自己)放到一个集合中，然后操作第一个点$j$，我们发现，如果$i\ne j$，则$i$不会被操作,所以$i$被操作当且仅当$i$为集合的第一个元素，所以$i$被操作的概率就为$i$是这个集合的第一个元素的概率，设集合大小为$siz$，则$i$被操作的概率就为$\frac{1}{siz}$,对他们求和即可。

又因为要对$998244353$取模，在模意义下没有乘法，所以$\frac{1}{siz}$就相当于模意义下$siz$的逆元，所以求出所有$siz$的逆元求和即可

sez663

题意给定两个字符串$S，T$，问至少删除$S$中多少个字符，使得$S$中不含有$T$
数据范围 $|S|,|T|\le 8000$
难点可能在于删了一个字符，剩下的两端字符串还会拼在一起，可能会出现新的$T$，所以直接删应该是不可能的。
考虑$DP$，设$f_{i,j}$表示在$S_i$这个位置匹配了$T$长度为$j$的前缀所需要删的最少的点，这样最后的答案就是$\min_{i=0}^{|T|-1} {f_{|S|,i}}$即可。
考虑如何转移：假设现在已经处理完了$f_{i,j}$，考虑如何向后递推。
如果删掉第$i+1$个字符，则$f_{i,j}+1\to f_{i+1,j}$
如果不删，则要找到一个$T$的最长前缀使得能够匹配上第$i+1$个字符，具体的，如果目前已经匹配到$T_j$，则要找一个最长的$border$使$border$的下一位能够匹配第$i+1$个字符，设该$border$的长度为$j'$，则$f_{i,j}\to f_{i+1,j'+1}$
整理一下可得

\[f_{i,j}+1\to f_{i+1,j}\\ f_{i,j}\to f_{i+1,j'+1} \]

$j'$为$T_j$的最长$border$的长度
因为要求$border$所以可以先预处理出来前缀数组，然后每次跳前缀数组即可

优化：

如果每次在匹配$S_{i+1}$的时候跳前缀数组，那么会超时，所以可以现予处理出来
设$trans_{j,c}$为在$T$串中处理到$j$并且将要处理$j+1$时，要匹配一个字符$c$应该跳到哪个位置

P4094 [HEOI2016/TJOI2016] 字符串

题目简介 给定一个字符串$S$,并给定$m$组询问，每次询问给定四个正整数$a,b,c,d$，要求回答$S[a..b]$的所有子串和$S[c..d]$的最长公共前缀。
数据范围 $|S|\le 100000$
第一次转化 能发现如果把原字符串建出反串，则问题转化成了求出最长公共后缀，那么就尝试可以利用$SAM$的强大的能力了
第二次转化 又能发现只需要判断$S[c..d]$的后缀在不在$S[a..b]$中即可，又因为可以维护出来$S[c..d]$的$endpos$集合，所以问题又可以转化成了查询在$a..b$区间中是否有$S[c..d]$的$endpos$

注意：上述的转化存在问题，因为即使一个字符串的$endpos$集合在$a..b$区间中，但是如果该字符串的长度为$2$，而$endpos$在$a+1$，实际上这个串在$S[a..b]$中不存在

所以我们需要枚举$len$,然后判断$a+len-1..b$区间中是否有$endpos$集合即可.
问题又来了，暴力枚举显然是会炸的，所以要考虑其他的方法
又不难发现：如果一个 $len$ 成立，则$1,2,\dots,len-1$也都成立，也就是满足单调性，所以可以考虑二分。
问题又来了：如何确定一个字符串的$endpos$集合。
思考一下能发现，一个字符串的$endpos$集合就是其在$parent$树上的子树中的$endpos$集合并，而集合并就可以用线段树合并来做。

那这道题的大致思路已经出来：

建出反串
建出 $SAM$，把前缀节点的线段树中该节点在原字符串中出现的位置标记为$1$
建出$parent$树，并把父亲节点的线段树与儿子节点合并
接受询问，先找出 $S[c..d]$在$parent$树上的节点（倍增求，否则会炸）
二分长度，找出长度对应的$endpos$集合（说白了就是 $S[c..d]$的长度为$len$的后缀的$endpos$集合）（倍增找）,然后查询该后缀的线段树中$a+len-1,b$区间是否有值。二分答案

注意：

倍增就是节点的父亲，如何判断字符串属于哪一个状态：看$len$，因为一个状态所代表的字符串的长度是连续的，所以只需要判断给定字符串的长度$len$是否小于等于该状态的$len$，找到深度最小的祖先即可

7.4

P3209 [HNOI2010] 平面图判定

题目简介：给定一张图这张图存在一个哈密顿回路（一个包含所有顶点的环），判断改图是否为平面图（所有边都不相交）
能发现可以把边分为两种，一种是在哈密顿回路内，一种是在哈密顿回路外（相当于一个点在圆内还是在圆外），如果两条边在哈密顿回路内相交，那么这两条边就必须一条在内一条在外，所以可以把他们看成一个四元组$i,a,j,b$($i,j$是边,$a,b\in\left\{0,1\right\}$表示$i,j$边在哈密顿回路内还是外)，那么这个问题就可以用$2-SAT$做了，相当于板子了。
还有一个重要的结论，平面图满足一个性质：$m\le 3n-6$，可以判掉一些测试点，具体证明看这里

注意：

因为是多组询问，所以每次询问要清空数组，并且$2-SAT$是要拆点，所以还需要开两倍数组，清空两倍

P6378 [PA 2010] Riddle

题目简介：给定一些点对$a,b$和一些点集，需要选出一些点，选出的点要满足每一个点对$a,b$点对要至少选出一个点，且每个点集中恰有一个点被选出
思路

首先点对的选法很确定，所以可以把一个点$x$拆成两个点$x,x'$表示$x$选还是不选，然后$a'\to b,b'\to a$连边即可。
点集的选法就有点问题了，因为如果暴力连$x'\to i(i\in$该点集除去$x)$是$n^2$的，会炸，这时考虑优化。因为点的拆法是固定的，所以拆点的过程就无法优化了，所以只能考虑优化建边。能发现一个点集内如果选择一个点则剩下的点都不选，所以选两个不同的点剩下的点的交集很大，所以考虑把这部分优化起来。

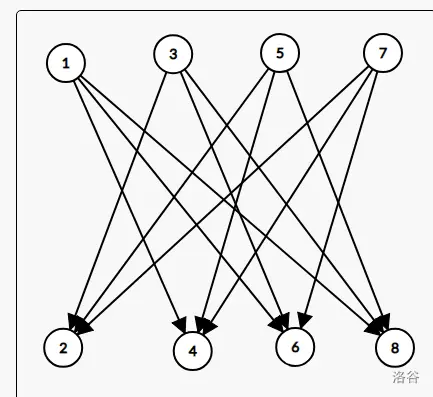
这是原来的建图（上面表示选，下面表示不选）
能发现这些点都无法改变，所以我们如果想优化建图，就需要找一些代替这些点的节点连边，并且使这张图的性质完全保留，那么就可以等到这样的图

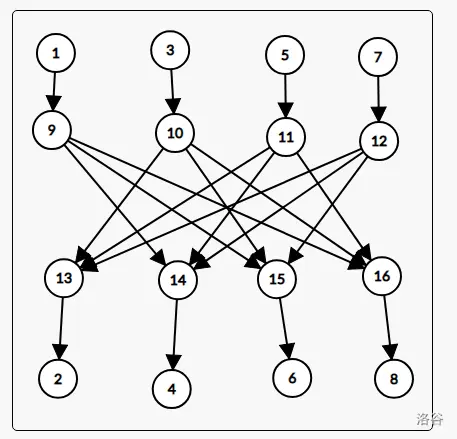
不难发现，边的数量并没有变少，甚至还变多了，但是，不难发现，$9\to 15$可以变成$9\to 10\to 15$,同理，$9\to 16$也能变成 $9\to 10\to 11\to 16$
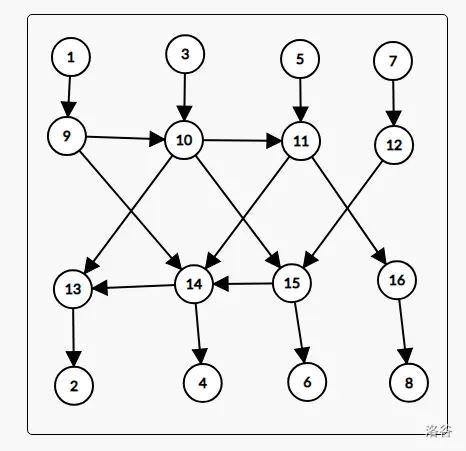
而对称一下，下面也同理可得，$11\to 13$可以变为$11\to 14\to 13$，其他同理，那么就能够得到这个：

边数虽然看起来减少了不少，但是有一个致命的问题：$1\to 9\to 14\to 13\to 2$，这是错误的，我们需要避免这样的问题，不难发现，$10\to 15$的目的就是为了走到$6$，所以可以直接让$10\to 6$，同理$9$也一样，利用同样的思路，能发现虽然我们不能让$3\to 10\to 13\to 2$的事情发生，但是我们可以让$3\to 13\to 2$的事情发生，注意我们也不能让$10\to 2$的事情发生，因为这样的话，就无法优化建图了（即无法使到达该节点$\leftrightarrow$到达该节点的前缀节点了），所以最终建图就是这样：

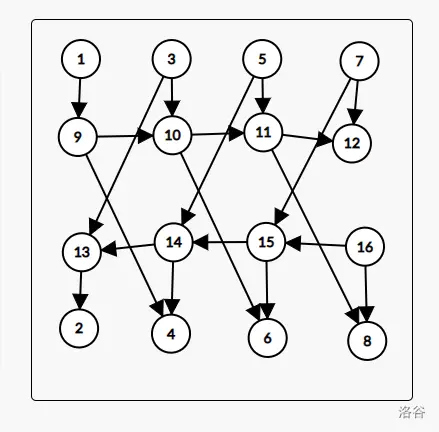
然后跑$2-sat$就行了

7.5

P3825 [NOI2017] 游戏

题目简介：给定一个长度为$n$的字符串$S$，要求构造合法的字符串序列$C$。$S_i\in \left\{x,a,b,c \right\}$, 其中$a$表示$C_i$不能为$A$,$b$表示$C_i$不能为$B$,$c$表示$C_i$不能为$C$,$x$表示$C_i$可为$A,B,C$任意值。再给定$m$组限制，每组限制的形式为$a,x,b,y (a,b\in \mathbb{Z},a,b>0,$ $x,y$为字符$)$，表示当$C_a=x$要求$C_b=y$

数据范围 $1\le n\le 5\times 10^4,1\le m \le 1\times 10^5$,$x$的数量不超过$8$

思路不难发现，如果$S$中不包含$x$，则一个点就只有两种选择了，那么该题就变成了$2-sat$题了，但是$S$中包含$x$。那么考虑如何消除$x$的影响，暴力一点就$3^8$枚举$x$是什么就可以了，总复杂度为$O(3^8n)$就炸了。考虑优化。又能发现$x=a$是能枚举$C_i=B$和$C_i=C$的情况，$x=b$时能枚举$C_i=A$和$C_i=C$的情况，那么只要枚举$x=a$和$x=b$的情况就能枚举完所有的情况了，所以复杂度变成了$O(2^8n)$了，那就可以了

$2-sat$连边方式：

能发现题目中的条件形式为当..成立时，...必须是...,那么怎么连边呢？假设一个条件为$i,0,j,1$（当$i$取$0$时，$j$一定取$1$），因为$2-sat$连的边时强制性的，所以肯定会连一条$i\to j'$的边（$x$代表$x$取$0$，$x'$代表$x$取$1$）但是这样就够了吗？经过我不断的交代码，得到了一个结论：不行。那么考虑还需要连什么边，暴力枚举一下，不难想到，还需要连一条$j\to i'$,因为当$j$取$0$时，$i$必不能取$0$，所以$i$一定取$1$。
如果有两个条件为$i,0,j,1$，$i,0,j,0$这种相互矛盾的选项时，那不难发现，$i$一定取$1$了，那么怎么在连边上体现这一点的？考虑最后取点的时候选择的时强连通分量编号小的那一个，所以可以连一条$i\to i'$，这样就能保证$i'$编号小于$i$也就能强制选$i'$了。利用这种方法，还可以解决诸如$i,0,i,1$的关系

那么到这，这道题就算完了，剩下的就只有打代码和实现细节了。

code

7.13

P1948 [USACO08JAN] Telephone Lines S

题目简述：给定一张无向图，$n$个点,$m$条边，每条边有个一权值$w$，可以将任意$k$条边的权值变为$0$, 要求从$1$到$n$的路径上最大边权的最小值
数据范围：$1\le n\le 10^3,1\le m\le 10^4,w\le 10^6$

思路：

看到最大值的最小值，可以想到二分答案，那么我们二分出一个最大边权$mid$如何判断合不合法呢？能发现，所有小于等于$mid$的边都无意义，所以可以看作为$0$，所有大于$mid$的边只要能删去就直接删，只要判断最少删去的边，也就是大于$mid$的边的个数，小于等于$k$就好了
当这里我们就能得出一个大致思路，二分答案$mid$，把图上的边小于等于$mid$的赋为$0$，大于$mid$的赋为$1$，然后跑$01BFS$求$1$到$n$的最短路，只需要判断$1$到$n$最短路径是否小于等于$k$即可

注意：

二分的边界和向上取整需要多思考一下

code

AT_arc084_b [ABC077D] Small Multiple

题目简介：给定一个正整数$K$, 求$K$的正整数倍的$S$，使得$S$的数位和最小
数据范围： $2\le K\le 10^5$

题目转化及思路：

能发现，每个数都可以由$1$通过加$1$和乘$10$的操作得来，则可以将$i\to (i+1)\mod K$，边权为$1$，将$i\to (i\times 10)\mod K$，边权为$0$，能发现点$0$所代表的就是$K$的倍数，最终答案就是$1$到$0$的最短路
因为边权都为$0$或$1$，所以可以直接用$01BFS$求最短路

code

7.14

CF293B Distinct Paths

题目简介 ：给定一个$n\times m$的方格图， $k$种颜色，有一些方格已经被涂上了颜色，需要将剩下的格子涂上颜色，要求使$(1,1)$到$(n, m)$的所有路径上，每个方格的颜色都不同，求合法方案数。
数据范围： $1\le n,m\le 1000, 1\le k\le 10$
对数据范围的分析：因为从$(1,1)\to (n,m)$的路径上一共有$n+m-1$个方格，所以如果$n+m-1>k$，则无论怎么填都不可能构造出合法方案，那么就可以把 $n, m$缩到很小的范围，可以考虑爆搜。
思路：

我们发现爆搜是$O(k^{n*m})$的，所以依然会爆，所以考虑优化
- 假设现在填$(x,y)$，从$(1,1)\to(x, y)$的路径上没有出现过的颜色种类为$k'$个，其中在全局中都没有出现过的颜色种类数为$k''$。能想到，对于这$k''$种元素，在$(x,y)\to(n,m)$其实是等价的，就是说，在$(x,y)\to(n,m)$的路径中，这$k''$种颜色可以互换，都不会让一条路径上出现相同的颜色。所以在$(x,y)$填$k''$种颜色的总方案数即是调其中一个颜色填进去的方案数$\times k''$即可，而剩下的$k'-k''$种颜色，暴力枚举即可
- 接下来考虑怎么存储$(1,1)\to(x,y)$(不包含$(x,y)$)路径上的出现过的颜色，因为$k\le 10$，则可以考虑用二进制存储，设$f_{i,j}$表示$(1,1)\to (i,j)$的所有路径中出现的颜色，那么能得出$f_{x,y}=f_{x-1,y}|f_{x,y+1} $($|$为或操作)。该问题解决
- 如果仅按当前思路交上去会发现是错的，问题出在了当填$(x,y)$时，假设要填$i$颜色，那么如果$(x,y)$右下角中含有$i$颜色，那么一定会出现一条路径有两个 $i$颜色，那么就不符合了，所以还需要存储$(x,y)$右下角出现过的颜色，这样做就$AC$了

P4053 [JSOI2007] 建筑抢修

贪心：详见代码理解

注意：

当一个任务不能被完成时，按照贪心应该让消耗时间最大的退出来，放入这个，但是实际上还需要判断是完成消耗时间最大的那个最后的时间长，还是完成该任务所用的总时间更长

P1792 [国家集训队] 种树

题目简介：给定$1$~$n$的编号，每个位置有一个贡献$a_i$，要求选出$m$个位置，使得贡献最大，并且选出的位置不相邻。（定义相邻为:$i,i-1,i+1$三个数相邻，特别的, $1$和$2, n$相邻，$n$和$n-1,1$ 相邻）
思路：

首先想到一个错误的贪心：每次选择最大的点，然后把其相邻的点删去，继续选直至选出$m$个点，但很容易就会被$hack$了
那么进行改造，当选择了一个点，则把该点$i$的值改为 $a_{i-1}+a_{i+1}-a_i$，这样再选该点的时候就相当于不选$i$而选$i-1,i+1$的方案了，就是一个反悔贪心。

剩下的细节都在代码里

7.15

CF1076G Array Game

题目简介：题面简化不了一点
博弈论的新题，博弈论有必胜态和必败态。这道题有一个挺好的性质，考虑当到了第$i$个位置并且$b_i-1$，那么如果$i$点的状态为先手必胜，那么就直接跳，如果不是就分类讨论

如果$b_i$为奇数，那么可以选择原地踏步，把先手必败的状态留给另一个人，那么这样就还可以保证先手必胜
如果$b_i$为偶数，那么无论怎么样都会是先手必败

进一步考虑，什么时候是先手必胜,首先$b_i$是奇数的时候，$i$这个点必定为先手必胜，其次考虑在$i$点，如果可以跳到一个先手必败的点，那么$i$就直接跳使得另一个必败，则$i$点就是先手必胜了

经过了以上的分析，可以发现一个点是必胜态还是必败态与其具体数值无关，只与其奇偶性有关，又因为到达该位置之后就会使该位置减一，而奇偶性说的是到达改点后的奇偶性，所以可以把$i$点的值设为$(a_i-1)\mod 2$了。那么考虑暴力，从后往前遍历，如果$a_i=1$则$dp_i=1$否则，看其后面$m$个是否有必败态，如果有，$dp_i=1$否则$dp_i=0$。最终输出看第一个位置的$dp$即可。考虑加一个数，如果加的数是偶数，则奇偶性不变，否则奇偶性改变，所以加奇数相当于区间反转。

我们发现一个位置的值只与其后面$m$个位置的状态有关，而$m$又很小，所以可以考虑二进制压缩。而如果知道了$[r+1,r+m]$的状态，就可以推出$[l,r]$的状态了，我们考虑如何快速的推出。我们设$f_{S}$为$[r+1,r+m]$的状态值压缩成$S$时，$[l,l+m-1]$的状态值为$f_S$。我们发现，如果已经知道$[r+1,r+m]$的状态值压缩成$S$时，$[mid+1,mid+m]$的状态值为$f'_S$，并且知道$[mid+1,mid+m]$的状态值压缩成$f'_S$时，$[l,l+m-1]$的状态为$f''_S$,能发现，当$r+1,r+m$ 的状态值压缩成$S$时，$[l,l+m-1]$的状态值为$f''_S$，也就是说$f_{1，S}=f_{2,f_{3,S}}$，($1$区间为$[l,r]$,$2$区间为$[mid+1,r]$,$3$区间为$[l,mid]$),我们发现这可以放到线段树上合并。

具体地说，在线段树的每个节点上维护一个$dp_{0/1,S}$表示其反转或不反的答案是什么，合并的时候就按照上面的过程进行合并。反转一个区间时，如果该区间被完全包含，那么$0/1$的答案就相当于直接互换过来。时间复杂度$O(2^m\log n)$

进一步的，我们发现，答案实际上只与后面$m$位有无必败态有关，所以可以把$2^m$变成$m$，就是把$S$变成$S$中第一个$0$出现的位置与左端点的距离，这样就把$2^m\to m$了，合并还是一样的。最终复杂度$O(mq\log n)$

此题细节很多，下面挑两个不好懂的细节进行讲解

if(l == r) {
    for(int i = 1; i <= m; i ++) {
        seg[p].dp[1].f[i] = seg[p].dp[0].f[i] = i + 1;
    }
    if(a[l] == 1) {
        seg[p].dp[0].f[m + 1] = m + 1, seg[p].dp[1].f[m + 1] = 1;
    }else {
        seg[p].dp[1].f[m + 1] = m + 1, seg[p].dp[0].f[m + 1] = 1;
    }
    return;
}

$f_i$就是$[r+1,r+m]$中第一个必败态出现的位置距$r$有$i$个位置时$[l,l+m-1]$中第一个必败态出现的位置距$r$有多少个位置

当边界值时只有一个点，所以$f_i=i+1$只是相当于平移，具体可以画图理解一下
当$a_l=1$时，该点为必胜态，而$f_{m+1}$就代表后$m$没有必败态，也就是说明从该点跳不到一个必败态，所以没反转前$f_{m+1}=m+1$就代表跳不出去，当$a_l=0$时，该点为必败态，所以前$m$ 个第一个必败态出现的位置就与$i$距离$1$了，
我们考虑$f_{m+1}$存的本质是什么，由于最底层赋值时$f_{m+1}=1$时第一个$dp$值为$0$，否则为$1$，向上合并的过程中$f_{m+1}=1$的唯一可能性就是$f_{右，m+1}=m+1$并且$f_{左，m+1}=1$，这时第一个$dp$值为$0$，否则为$1$，所以最后输出$1+[f_{m+1}==1]$

code

7.16

P1407 [国家集训队] 稳定婚姻

题目简述：有$n$对夫妻，$m$对有过恋情的人，当一对夫妻感情出现问题，例如$B_i,G_i$感情不合，则$B_i,G_i$会找他们的前任或前前任以此类推，如果$B_i$找到了$G_j$，则$G_j$会和$B_j$离婚然后和$B_i$私奔，然后$B_j$找他的前任或前前任，一系列离婚事件和私奔事件就会发生，如果最终还能匹配成为$n$对夫妻，我们就称第$i$个婚姻为不安全的，否则就为安全。最终询问每场婚姻是否安全
数据范围：$1\le n\le 4000,1\le m\le 20000$

方法：考虑一种连边方式，正常夫妻女指男，前任则男指女。我们考虑这样连的含义，假定从$G_i$开始走，走的过程一定为$G\to B\to G\dots$，我们发现这个过程就是~~被绿和绿~~离婚和私奔的过程，如果最后能够再走到$B_i$，则说明可以通过这样的方式再次使$B_i$匹配上夫妻，而$B_i\to B_i$的路径上的每一个人都会匹配到夫妻，最后也就会有$n$对夫妻，$i$这对婚姻不合法。

进一步地，思考$G_i$能走回$B_i$意味着什么，因为$B_i\to G_i$，所以这个性质又意味着$B_i$和$G_i$在一个强连通分量中，而该条件又是$G_i$能走回$B_i$的充要条件，所以只需要判断$G_i$和$B_i$是否在同一个强连通分量中即可

P2272 [ZJOI2007] 最大半连通子图

一个强连通分量必定是半联通子图，所以考虑强连通分量如何组成半联通子图，仔细想一下就是缩完点在$DAG$上找到一条点权最大的链
这道题上在这没什么，主要是细节：

注意：

做完$tarjan$后缩点需要建新图时，因为需要在$DAG$上做$dp$，所以需要去除重边，和多加的入度，想到这里用$map$去重即可

CF618F Double Knapsack

题目简介：给定两个长度为$n$的可重集$A,B$，$\forall x\in A,B\le n$，要求构造两个子集和相等
数据范围；$1\le n\le 10^6$
思路：

强化限制条件，找出原集合的两个连续集合，找出一个合法解。
- 首先证明有解：考虑把$A,B$集合的前缀和集合列出$P,Q$(以下称为序列$p,q$)，钦定$q_n\le p_n$，然后如果在$A$集合选择区间$[l_1,r_1]$,在$B$集合选择区间$[l_1,r_2]$，那么就会有$q_{r_1}-q_{l_1-1}=p_{r-2}-p_{l_2-1}$,移一下式子得到：$q_{r_1}-p_{r_2}=q_{l_1-1}-p_{l_2-1} $,那么我们考虑找出两个二元组$(i_1,j_1),(i_2,j_2)$满足上面的条件并且$i_1<i_2,j_1<j_2$,那么我们考虑$\forall i\in [0,n]$，找到最小的一个$j$使得$q_j\le p_i$,发现因为$q_n\le p_n$，所以对于$\forall i$一定可以找到一个$j$，这样我们能找到$n+1$个形似$(i,j,q_j-p_i)$三元组，而$q_j-p_i\in [0,n-1]$，（因为集合中的任意元素都$\in[1,n]$,如果$q_j-p_i\ge n$，那么不选$j$，则$q_{j-1}-p_i\in [0,n-1]$了），根据抽屉原理，至少会有两个三元组使得第三个值相等，那么就能构造出解了

实现：
因为前缀单调递增，所以可以用双指针找到每一个$i$对应的$j$，在双指针扫的过程中记录下 $q_j-p_i$, 并且记录下其$i,j$即可$O(n)$做了。

7.17

P4630 [APIO2018] 铁人两项

题目简述：给定一张$n$个点,$m$条边的无向图，要求找出三元组$(a,b,c)$满足$a\to b$的路径上可以经过$b$，求出一共有多少这样的三元组。
数据范围：$1\le n\le 10^5,1\le m\le 2\times 10^5$
思路：

考虑在同一个点双内，两点之间的三元组总数就是点双的大小减去$2$。
在不同点双内，则两点之间三元组总数为所有点双的点的个数减去割点的数量再减$2$。
根据第$2$点，可以建出圆方树，将方点的点权设为点双的数量，圆点的点权设为$-1$,这样，两点之间的三元组总数即是圆方树上两点之间的点权和。

大体思路已经确定。

注意：

再找点双和建圆方树的时候，退栈的时候，栈顶到$v$的时候就应该停止，然后把$u,v$都加入点双

if(dfn[u] <= low[v]) {
    int s = ++ num;
    val[s] = 1;
    while(stk[top] != v) {
        int t = stk[top --];
        ead(t, s);ead(s, t);
        val[s] ++;
    }
    ead(u, s);ead(s, u);
    ead(s, v);ead(v, s);
    top --;
    val[s] ++;
}

P2371 [国家集训队] 墨墨的等式

题目简述：给定长度为$n$的序列，$a_{1\dots n}$和$l,r$，询问有多少$b\in[l,r]$可以使$\sum_{i=1}^{n}a_ix_i=b$存在非负整数解
数据范围：$1\le n\le 12, 0\le a_i\le 5\times 10^5,1\le l,r\le 10^{12}$

方法：同余最短路

选一个大于$0$的$a_i$，在模$a_i$的情况下建图，点为$0,1,\dots,a_i-1$
考虑一个$a_j(i\neq j)$，在一个点$k$，可以连$k\to (k+a_j)\mod a_i$，边权为$a_j$，对每一个$k,a_j$都这么做。

我们思考这么做有什么用。发现这样连边，是可以求出在模$a_i$意义下，可以求出最小的，加起来同余$k$的几个数的和。这样，就可以在此基础上加上若干个$a_i$，最终加到$[l,r]$区间，即可求出答案

注意：

要注意，最为模数的$a_i\neq 0$。

code

P2662 牛场围栏

直接说结论: 同余最短路处理最大不可达问题
考虑最终求出来了$dis_i$表示$x\equiv i(\mod a_1)$的$x$的最小值，那么所有大于$x$并且同余$i$的所有数，都可以通过加$a_i$获得，所以对于同余$i$来说，$dis_i-a_1$就是最大不可达值，那么$\max_{i=0}^{a_1-1}dis_i-a_1$就是最终的答案。

无解情况：

有$1$参与，那么所有数都会被表示出来，也就不会有不可达值了
设原序列为$a_1,a_2,\dots,a_n$,若所有值的$\gcd\neq 1$，那么不会有最大值，考虑证明：
设$d=\gcd(a_1,a_2,\dots,a_n)$,则$d|a_1\times x_1+a_2\times x_2+\dots a_n\times x_n$,所以$d|m$是$m$能够被表示出来的必要条件，那么考虑$\forall m,d\nmid m$都不能表示出来，如果$d\neq 1$，那么就不存在最大值了

code

7.20

CF715C Digit Tree

前置知识：模意义下的乘除，点分治，求逆元

题目简述：给定一颗树，每条边的边权$1\le w\le 9$，给定一个正整数$M$，保证$\gcd(M,10)=1$,要求求出所有有序点对$(u,v)$，满足从$u\to v$的简单路径上按顺序写下他在路径上遇到的所有数字（从左往右写），得到的十进制整数可以被$M$整除。求出所有满足该条件的有序点对。
数据范围:$n\le 10^5, M\le 10^9$
思路：

考虑给我们的$\gcd(M,10)=1$有什么用。能发现当满足该条件时,$10$在模$M$意义下有逆元
在考虑什么时候点对才会出现，我们记$u, v$的$lca$为$x$, 从$u\to x$的路径上的数都写下来为$a$, 从$x\to v$的路径上的数都写下来为$b$，$b$的位数为$w$, 则当$a*10^w+b\equiv 0(\mod M)$时，该点对才会贡献答案。继续对该式子进行转化，可得$a\equiv -b*10^(-w)(\mod M)$,也就是$a\equiv (M-b)*(10^{-1})^{w}(\mod M)$，而$10$在模$M$意义下有逆元，设为 $inv$ ，则$a\equiv (M-b)*inv^w(\mod M)$。
考虑把顶点固定，用桶维护式子左右两边的值，那么就可以用点分治做了

注意：

给定的$M$不是质数，而费马小定理只能求模数是质数的逆元，所以该题要用$ex$_ $gcd$求逆元
详解：
把$10$看作$a$, $M$看作$b$, 等到方程$10x+My=1$，我们要求解出$x>0,y<0$的一组解，用$ex$_ $gcd$ 求即可。因为$y$是负数，所以相当于$10x\mod M = 1$，所以也就找到逆元了

code

7.21

P4211 [LNOI2014] LCA

题目简述：给定$n$个节点的有根树，根为$1$，定义一个点的深度为该点到根的距离$+1$,有$m$次询问，每次询问给出$l,r,z$，求$\sum_{i=l}^{r}dep[LCA(i,z)]$
数据范围：$1\le n\le 5\times 10^4, 1\le m\le 5\times 10^4$

转化：

首先第一步，$\sum_{i=l}^{r}dep[LCA(i,z)]=\sum_{i=1}^{r}dep[LCA(i,z)]-\sum_{i=1}^{l-1}dep[LCA(i,z)]$,也就是改成求一个前缀了
考虑$dep[LCA(i,z)]$是什么，是$LCA(i,z)$到根有几个点（包括本身）,那么可以将$i\to 1$的路径上的点都$+1$,然后求 $z\to 1$路径上的点权和。$i$有多个也是一样，只要把所有$i\to 1$的路径上的点权都$+1$, 最后查询就能求出答案了。

到这里，问题雏形已成，把询问离线下来，分别求$[1,l-1]$和$[1,r]$，利用双指针维护过程，树剖和线段树加点权的查询答案

code

P4766 [CERC2014] Outer space invaders

题目简述：有$N$个外星人进攻，第$i$个进攻的外星人会在$a_i$出现，必须在$b_i$前杀死，距离我的距离为$d_i$。有一个武器，可以消耗$R$的代价消灭$R$以内的所有外星人。求摧毁所有外星人的最低成本。
数据范围：$1\le n\le 300, 1\le a_i, b_i, d_i\le 10^4$
思路：首先发现$a_i,b_i$的实际大小并不关注，只关注他们的相对位置，所以可以离散化。然后，发现爆搜肯定过不了，所以考虑$DP$。一开始可能会想到把$d$排序，然后线性$dp$做，但是发现还有一个时间的问题，一个外星人只会在$[a_i,b_i]$出现，所以不妨设$f_{l,r}$为时间在$[l,r]$内所有外星人都被消灭的最小代价。考虑：$[l,r]$内区间的一次攻击必定是针对距离最远的那个（设其区间为$[L, R]$）。把其攻击掉就可以将其余与$[L, R]$有交的区间都杀掉了，而与他无交的就放在其他区间进行处理。那么可得转移$f_{l,r}=min_{k=L}^{R}f_{l,k-1}+f_{k+1,r}+D$ ($[L, R]$为距离最远的区间，$D$为其距离)，时间复杂度$O(n^3)$

注意：边界条件需要好好琢磨一下

code

CF1572E Polygon

题目简述：给定一个凸$n$边形，需要$k$条分割线，两两之间不交，使得分出的$k+1$个多边形面积的最小值最大
数据范围: $1\le n\le 200$

前置知识：已知三角形坐标求三角形面积：$S=\frac{1}{2}((x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1))$

思路：这个$dp$很难想啊。首先看到最小值最大，那么就本能的想到二分，那当我们二分出$mid$后，该怎么写$check$函数呢？其实就是判断是否可以把该多边形分成大于等于$k+1$个面积大于$mid$的多边形。如何判断呢？显然贪心是不太行的，然后看到$n\le 200$，~~能想到~~区间$dp$，我们设$f_{l,r}$表示用$[l,r]$的点最多能分出多少面积大于等于$mid$的多边形。那么考虑转移，因为这算是区间$dp$，所以有一个常有的套路即是枚举区间之间的断点，那么可得转移，$f_{l,r}=\max_{k\in [l,r]}f_{l,k}+f_{k,r}$。但是仔细一想发现有问题，如果这样转移，那么$l,k,r$组成的三角形就不会被统计在内，同理，$f_{l,k},f_{k,r}$也会有多余的情况没有统计在内，最终会导致$f_{l,r}$的答案偏小，怎么解决？考虑把剩下的面积记录下来，即$g_{l, r}$表示在$f_{l,r}$最大的情况下留下来的面积。因为留下来的面积都在$[l,r]$组成多边形的外端，所以$l,k,r$组成的三角形的面积可以和$f_{l,k},f_{k,r}$残留下来的面积拼在一起组成新的多边形，那么即可得到最终的转移方程式：

\[f_{l,r}=\max_{k\in [l, r]}f_{l,k}+f_{k,r}+(mid\le area(l,k,r)+g_{l,k}+g_{k,r}) \]

$g$就按照上面所说进行转移即可

7.22

P5336 [THUSC 2016] 成绩单

题目简述：有$n$张成绩单，第$i$张成绩为$w_i$,每次可以选择一段连续的区间进行发放（如果发放下去了一个区间，则剩下的区间会拼在一起），要求最小化$A * k + \sum_{i=1}^{k}B*(mx_i-mi_i)^2)$,($A,B$是给定的常数，$k$为发的次数，$mx_i,mi_i$分别为第$i$批发的成绩单成绩的最大值和最小值)
数据范围：$n\le 50$
思路：很容易能设出$g_{l,r}$表示$[l,r]$区间内的数都被删完的最小代价，但是单有这个也无法转移。考虑，删除一个序列，只关心他的最大值和最小值，所以不妨再设一个数组$f_{l,r,a,b}$表示$[l,r]$区间内，最后一次删的数的值域在$[a,b]$之内的最小代价，那么$g_{l,r}=\min (f_{l,r,a,b}+A+B*(b-a)^2)$，接下来考虑$f$如何转移，继续应用区间$dp$的套路，枚举断点。找到一个断点$k$,则，最后要删得数值域在$[a,b]$内会有几种情况：

$[l,k]$都拿完了，剩下$[k+1,r]$中值域$[a,b]$的数
剩下$[l,k]$中值域$[a,b]$的数，$[k+1,r]$都拿完了
$[l,k],[k+1,r]$都剩下$[a,b]$之间的数

所以得到转移：

\[f_{l,r,a,b}=\min (g_{l,k}+f_{k+1,r,a,b}) \]

\[f_{l,r,a,b}=\min (f_{l,k,a,b}+g_{k+1,r}) \]

\[f_{l,r,a,b}=\min (f_{l,k,a,b}+f_{k+1,r,a,b}) \]

\[g_{l,r}=\min(A+B*(b-a)^2+f_{l,r,a,b}) \]

AT_agc035_d [AGC035D] Add and Remove

题目简述：给定一个卡牌序列，每次可以取出三张，把中间一张的权值加到旁边的两张上，求最后两张权值和的最小值。
数据范围：$n\le 18$
思路：正着考虑没什么思路，根据正难则反，考虑一个数会对答案产生多少贡献，考虑如果有三个数，$a,b,c$，$a$对答案的贡献为$xa$, $c$对答案的贡献为$xc$,那么如果删除掉$b$,则$b$对答案的贡献就是$xa+xc$，对一个区间$[l,r]$来说，如果$l$对答案的贡献为$xl$，$r$对答案的贡献为$xr$,则最后一个删除的数对答案的贡献就是$xl+xr$，那么不妨枚举最后一个删除的数，设其位置为$i$,则$[l,r]$区间内被删完只剩下$l,r$的代价就为删掉$(l,i)$的代价加上删掉$(i,r)$的代价加上$a_i*(xl+xr)$，那么不妨设$f_{l,r,xl,xr}$为将$l,r$对答案的贡献分别为$xl,xr$时$[l,r]$内删到只剩下$l,r$的最小代价，那么可得转移：
$f_{l,r,xl,xr} = \min_{k=l+1}^{r-1}f_{l,k,xl,xl+xr}+f_{k,r,xl+xr,xr}+a_k*(xl+xr)$
这是将$k$钦定为最后删除的那个点时的转移，因为$k$对答案的贡献次数就是$xl+xr$，所以直接用$f_{l,k,xl,xl+xr},f_{k,r,xl+xr,xr}$更新即可

注意：这道题写区间$dp$会挂，因为$xl, xr$的增长是斐波那契数列，因为可以看做是$1,1,2,3,5,8,\dots,$,所以数组开不下，要写爆搜，能过就是了

AT_agc034_e [AGC034E] Complete Compress

题目简述：给定一棵$n$个节点的树，树上的一些节点存在棋子，每次可以把两个距离大于$2$的棋子向他们中间挪动一个，询问是否存在一种操作序列使得所有棋子最终能跳到同一个点上，如果存在，输出最少的操作次数，否则输出$-1$。
数据范围:$n\le 2000$

题解：

$n\le 2000$看着像是$O(n^2)$做的。那么如果钦定一个点为最终跳到的节点，能在$O(n)$时间复杂度内求出操作次数，就可以过了。

那么钦定一个点为根，所有点向上跳，求跳到该点最少的操作次数。首先对题意进行转化，发现棋子向上跳的过程中可以拆成$deep$个状态，那么我们把这些状态具象化，将该点到根的路径上的点放一颗棋子（不同于原题给的棋子），那么向上跳一个点就相当于删去一个状态。那么问题可以转化成，在树上的若干个节点上有一些棋子，每次可以选择两个不在同一条链上的棋子删除，问，最少多少次能删完。考虑递归操作，假设现在在处理以$x$为根的子树内的答案，我们首先让$x$的不同子树进行删点，我们发现，如果存在一个点$v\in son(x)$，满足$sum_v>sum_x-sum_v$,也就是$v$子树内的棋子的数量大于其他子树内棋子数量的总和。那么将其他子树内的所有棋子与$v$子树进行删除操作，最终$v$子树还会剩余棋子，为了将棋子都删完，我们递归操作，去到$v$子树里进行删点，直到$v$子树内的棋子数量大于其他子树内棋子数量的总和，为了知道是否可以达到该条件，还需要一个$f$数组，$f_x$，表示，$x$子树内可以进行的最多删除次数，那么只需要判断$sum_v-2*f_v$和$sum_x-sum_v$的大小即可了。这时，发现该子树内棋子的数量小于等于其他子树内棋子的数量总和了，有一个结论时，当满足该条件时，一定能够将$x$子树内个点都删完（具体等会再证），那么$f_x=\lfloor \frac{sum_x}{2}\rfloor$了.但是还少考虑了一种情况，即$sum_v-2*f_v>sum_x-sum_v$，时，即将$v$子树内能删的点都删完还是比其他子树内棋子的数量总和大时。那么以$x$为根的子树最多能进行的操作数$f_x=f_v+sum_x-sum_v$，最后，如何判断无解，如何判断操作次数呢？首先发现，因为每次操作都会删除两个点，所以$sum_root\equiv 1(\mod 2)$时一定无解。其次，如果$f_root< sum_root/2$时，说明操作次数不够多,还会有点没有跳到根上，所以也无解。而上面的算法流程又保证了有解时$f_root=sum_root/2$，所以最终只需要输出最小的$f_root=sum_root/2$了
解释:上文所提及的$sum_x$数组表示的是以$x$为根的子树里的棋子总数量，而所有$sum_x-sum_v$的式子中，$sum_x$是不包含$x$的

证明：

首先解释摩尔投票：~~(虽然没想都为什么要解释)~~
定义绝对众数为一个长度为$n$的序列中，出现次数$>\lfloor\frac{n}{2}\rfloor$的数，摩尔投票可以在时间复杂度为$O(n)$，空间复杂度为$O(1)$求出绝对实数，具体算法流程为记录一个$cnt,now$，然后不断加入数，设加的数为$x$，如果$x\neq now$，则$cnt--$，当$cnt=0$时，$now=0$，当序列的数加完后，$now$就是绝对实数。
其次，我们把$x$的儿子子树内，即$v\in son(u)$的子树内染上染色，不同子树染不同染色（只给放棋子的点染），然后将颜色按照颜色个数进行排序，每次选择颜色个数最多和次多的两个颜色将他们的次数减$1$，然后放回去再排序，重复操作，最后一定只剩下一个颜色或零个，如何理解呢？可以考虑画一个数轴，横坐标为颜色编号，纵坐标为颜色出现的次数，将所有坐标连起来可以的到一个类似阶梯状的图形，每次选择最大和次大的两个颜色减$1$，就相当于把阶梯进行坍塌，最终一定能坍塌成零层或剩下一个颜色（选择两个相邻的颜色进行坍塌，比较好理解），那么就证毕了

7.23

P6075 [JSOI2015] 子集选取

思路：

考虑把集合拆成$n$个元素去做，如果设一个元素在边长为$k$的三角形的方案数为$f_k$，则$n$个元素就是$f_k^n$,所以求出一个元素就好
把$A_{i,j}$有该元素设为$1$，否则为$0$，那么据题已知，当$A_{i,j}=1$，则$A_{i,j-1}=1,A_{i-1,j}=1$，换句话说，就是一个点为一，则其上面和左面的点也为一，所以所有的$1$会是一整块，那么问题就转化成了在$k$层的三角形里，放入一些$1$，如何让所有的$1$构成自上到下的连通块的方案数
再次转化，发现$1$和$0$会形成分割线，并且分割线不会越过$(1,1),(k,k)$的对角线，所以分割线的长度恰好等于$k$,那么问题又可以转化成了，从左下角开始，每次向上走或向右走，走$k$步，路径的总方案数。那么就是$2^k$，所以最终的答案就是$2^{kn}$

7.24

P1484 种树

用$wqs$二分，具体过程如下：(设$f_{i,j}$表示考虑到第$i$个位置，种了$j$棵树的获利最大是多少)

暴力$dp$为：$f_{i,j}=\max(f_{i-1,j},f_{i-2,j-1}+val[i])$时间复杂度$O(nk)$
发现一个性质，当$k$增大的时候，$f_{n,k}$也会增大，但是随着$k$越来越大，$f_{n,k}$的增速会变得越来越小，所以如果把$k$看作横坐标，$f_{n,k}$看作纵坐标，则$f_{n,k}$的函数图像整体呈凸分段函数，那么能发现该函数的斜率是不断减小的，符合单调性，那么就可以二分。如果有一个点被相切，且横坐标$x<k$，则，切$k$的斜率一定更小一点。那么反过来，知道一个斜率，如果能找到其所对应的$x$，则就能判断该斜率与切$k$的斜率的大小关系了，而我们如果找到了切$k$的一次函数的斜率，并且知道该一次函数与$y$轴的交点，那么就可以求出$f_{n,k}$了。那么问题就转化成了给定斜率，求出其与凸包相切的$x$和$b$。
发现，相切有一个性质，在上凸包中，相切的$b$一定是最大的，斜率是二分出来的，那么考虑如何求$b$。发现$b=y-xk$($k$为斜率)，那么就等效为，每种一个树都要消耗$k$的代价，所以只需要在$dp$的过程中加入该代价即可，最终，要求的就是$y-xk$的最大值，那么有转移式子$f_i=max(f_{i-1},f_{i-2}+a_i-k)$，(相当于不考虑原题有$k$的限制，直接求出最大的即可)，那么最终$f_n$就是$b$,在转移的过程中还需要记录下一个$g$，表示$f_n$最大的时候$x$是多少，判断$x$与$k$(原题的$k$)的大小，二分即可，最终的答案就是$f_n+g_n*mid$($mid$为二分出来的斜率)

参考代码

CF713C Sonya and Problem Wihtout a Legend

题目简述：给定一个序列$a_i$，每次操作可以给任意元素加$1$或减$1$,询问至少多少次操作可以把原序列改成严格递增的
数据范围：$n\le 3000,a_i\le 10^9$

题解：

首先原问题可以转化成求非严格递增的问题，即把每一个$a_i-i$,这样让$a_i-i$为非严格递增，则$a_i$就为严格递增了（下文就以$a_i$指代$a_i-i$）
考虑这样怎么做，首先暴力$dp$，设$f_{i,j}$表示第$i$位为$j$的最小操作次数，那么可得转移$f_{i,j}=\min_{k\le j}f_{i-1,k}+|a_i-j|$,时间复杂度是$O(na)$显然不能接受
考虑优化，发现$f_{i,j}$实际上是由若干个$|a_i-j|$拼起来的函数，也就是说其是一个凸分段函数，那么这里不用斜率二分，而采用一种叫$slope trick$的做法：

$slope trick$做法是对一些凸分段函数，可以只维护最开始的$k$(斜率)，和每个拐点的位置。具体的，会开一个$slope trick$数组，里面存储的是$a_i$这种元素，表示当横坐标为$a_i$时，凸分段函数的斜率增加$1$，（这是上凸函数，如果是下凸分段函数，那么就应该是减$1$）。如果需要维护前缀$\min$，则相当于找到第$1$个斜率大于$0$的上一个点，把其后的元素都删掉，只保留这点，相当于什么呢，相当于把凸分段函数开始向上升的内一段抹平。

那么对于该题，发现$min_{k\le j}f_{i-1,k}$就相当于一个前缀$\min$形式，如果把前缀$\min$的形式$f_{i-1,j}$的形式，即$f_{i-1}$函数上，每一个$j$点代表的是$f_{i-1}$的前缀最小值。
那么再看$|j-a_i|$，发现其实就是关于$j$的一个函数，并且是一个凸分段函数，拐点为$a_i$，前半段的斜率为$-1$，后半段的斜率为$1$。
那么现在要做的就是把前缀$\min$函数$f_{i-1}$和$|j-a_i|$函数合并起来。首先考虑拐点的加减，因为$|j-a_i|$中$a_i$是拐点，所以在$f_{i-1}$上，也会多出一个$a_i$的拐点。接下来考虑斜率，因为$|j-a_i|$前半段斜率$-1$,后半段$1$,所以相当于给$f_{i-1}$的$a_i$前半段$-1$,后半段$+1$，那么如何放在$slope$数组上呢。因为$slope$数组很像一个斜率前缀和数组，所以就相当于初始斜率$-1$,然后到$a_i$这个位置$+2$，也就是向$slope$数组里塞两个$a_i$。最后考虑如何抹平，也就是维护前缀$\min$。首先在$f_{i-1}$时，已经塞了$i-1$个$|j-a_i|$这样的绝对值函数了，每次加都会给初始斜率$-1$，所以现在初始斜率为$-(i-1)$，然后又因为$slope$数组里每一元素都会给斜率$+1$,而最后斜率变为了$0$，所以一共加了$i-1$个$1$,所以一共有$i-1$个元素，而在$f_i$时，又塞了一个绝对值函数，所以初始斜率变为了$-i$，但是，刚刚的操作向$slope$数组里塞了两个$a_i$，所以现在一共有$i+1$个元素，说明最后一段的斜率为$1$，为了保证前缀$\min$，所以需要把最大的元素删掉（因为在凸分段函数上越靠后，越接近斜率大于$0$的函数段）。那么操作就基本上完了。
回忆一下，我们需要的操作是向一个集合里插入两个元素，然后返回最大的元素并弹出，那很明确了就是堆。

最终还差一步，统计答案，当求出$f_n$的前缀$\min$函数（凸分段函数），发现需要求得是元素最大的纵坐标，那么怎么求呢？发现$slope$数组里的元素相邻两个之间连边，斜率是从$-1$变到$-n$的，那么利用三角函数和初中学的坐标系的知识，发现$y=b-(x_n-x_{n-1})-2(x_{n-1}-x_{n_2})-,\dots,-(n-1)(x_2-x_1)-n(x_1-x_0)$($b$为凸函数与纵坐标的交点)，拆一下式子发现，$y=b-x_1-x_2-x_3,\dots,-x_n$，那么只需要把堆里的元素扔出来然后减掉就可以了

8.5

P3391 【模板】文艺平衡树

题目：需要维护一个长度为序列，一开始序列为$1,2,\dots,n$，要求支持区间反转操作，一共有$m$次，输出最终序列
数据范围：$1\le n\le 10^5$

题解：

利用$Splay$,简单说一下$Splay$，与普通平衡树不同的是，普通平衡树维护平衡的方式是将每个点都赋上一个$rand$，$splay$维护平衡的方式是不断的旋转，把进行操作的点旋转到根，根据势能分析（我不会）能知道这样的均摊复杂度是$O(\log n)$的，话都在代码里了，注意看$rotate,Find$

code

注意：

打标记和线段树很像
注意$r=n,l\neq 1$时的特判（在主函数里）

8.6

P6136 【模板】普通平衡树（数据加强版)

注意：$splay$写法要求在任意操作后都要进行$splay$，例如，插入，求排名，求排名为$k$的权值，求前驱，求后缀，不然会$T$

P4097 【模板】李超线段树 / [HEOI2013] Segment

题解：

如题所述，需要用线段树，但是现在线段树里存的是经过区间终点的线段的纵坐标的最大值的线段编号。
直接说操作吧，有点难想，考虑对一个区间$[l,r]$，如果下方一个线段，用斜率$k$，和纵截距$b$来表示，设原线段为$l_1$，新插入的线段为$l_2$ ,中点的纵坐标分别为$val>ins$，如果$ins>val$，则判断$k_1l+b_1$和$k_2l+b_2$的大小，如果左边大，就把$l1$下放到左区间，如果右边大同理，把$l1$下放到右区间。如果$ins<val$，其实和上面的情况是相同的，相当于反过来做了。如果$ins=val$，首先把该区间对应的线段编号更新一下，然后线段下放的原理相同。
寻找答案，如果要找$x=k$与所有线段的，那么就要找在线段树上所有包含$x$的区间的纵坐标的最大值的最小线段编号。

注意：此题需要卡精度，判断等于的时候要这样：$a=b\to |a-b|\le eps$

code

AT_agc063_b [AGC063B]

题目简述：给定一个长度为$n$序列$a$,$a_i\in [1,n]$，定义一个序列合法为该序列可以由空序列通过以下操作得到：

选定一个正整数$k$，把$1,2,3,\dots,k$插入到原序列的某一位置。具体地，如果原序列长度为$m$，则可以将原序列改为$\forall i\in [0,m],a_1,a_2,a_3,\dots,a_i,1,2,3,\dots,k,a_{i+1},\dots,a_n$
询问原序列有多少个合法的连续子序列。
$1\le n\le 10^5$
题解：

观察合法的序列的性质，能发现最坏的情况就是$1,\dots,2,\dots,3,\dots,\dots,k$,而权值相邻的两个数，如$1,2$,之间的序列一定是合法的
由上面的性质，就可以判断一个区间是否合法了，做法是，开一个栈，将区间从左到右依次加入栈，设当前加入栈的元素是$x$，如果$x=1$，则直接插入，否则判断栈顶元素是否等于$x-1$,如果等于，就直接插入，否则就将栈顶的连续的一段$1,\dots,k$的序列全部删除，然后重复判断栈顶是否等于$x-1$，如果栈空了，则该区间不合法。回忆刚才的过程，能发现，弹栈，相当于插入一段$1,\dots,k$的序列。
那么如何统计所有的答案呢，考虑固定右端点，找出所有合法的左端点。首先左端点要是$1$,其次，如果$1$，在刚才的过程中被弹了出去，说明从当前点到右端点有一段是无法平成连续的序列的，例如$stk:1,2,3;insert 5$，此时会将$1$弹出，说明从这个$1$到右端点是不合法的。所以综上所述，右端点固定时，答案就是栈内$1$的个数

posted @ 2025-06-26 10:29 lghjl 阅读(20) 评论(0) 收藏举报

刷新页面返回顶部

注意：\(\sum_{i=1}^{n}(x_i-y_{i + k}+c)^2\)，这个式子里， 给x加时，c>0,给y加时，c<0，代码中c不能从0开始枚举

西安集训3.26 t2

注意：

坑点

注意：建分层图的时候先建出k层，再在k层之间连边

dij不能解决有负边的最短路！！！！！！！！

P5410拓展KMP/Z函数

注意的点

6.25

6.26

\(g\)更新\(f\)

\(f\)更新\(g\)

注意：

前置知识：高维前缀和，欧拉筛，埃式筛

做法：

注意：

6.27

前置知识:高维前缀和，分解质因数，随机化

方法1：

方法2：（题解）

注意：

思路：

注意：

补充：

6.28

思路:

注意：

题目思路

注意：

6.29

6.30

注意：

注意：

注意：

7.1

注意：

小优化：

7.3

优化：

注意：上述的转化存在问题，因为即使一个字符串的\(endpos\)集合在\(a..b\)区间中，但是如果该字符串的长度为\(2\)，而\(endpos\)在\(a+1\)，实际上这个串在\(S[a..b]\)中不存在

注意：

7.4

注意：

7.5

\(2-sat\)连边方式：

7.13

思路：

注意：

题目转化及思路：

7.14

注意：

7.15

7.16

注意：

7.17

注意：

方法：同余最短路

注意：

7.20

前置知识：模意义下的乘除，点分治，求逆元

注意：

7.21

转化：

注意：边界条件需要好好琢磨一下

前置知识：已知三角形坐标求三角形面积：\(S=\frac{1}{2}((x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1))\)

7.22

注意：这道题写区间\(dp\)会挂，因为\(xl, xr\)的增长是斐波那契数列，因为可以看做是\(1,1,2,3,5,8,\dots,\),所以数组开不下，要写爆搜，能过就是了

题解：

证明：

7.23

思路：

7.24

题解：

8.5

题解：

注意：

8.6

注意：\(\sum_{i=1}^{n}(x_i-y_{i + k}+c)^2\)，这个式子里，给x加时，c>0,给y加时，c<0，代码中c不能从0开始枚举