图的特殊点集和边集 学习笔记

支配集

一张无向图，如果一个点集使所有点要么在点集中，要么与点集中的一个点相邻，则称这个点集是图的一个支配集。最小支配集大小记作 \(\gamma(G)\)。求一般图的最小支配集是 NP-hard 的。

考虑如何求树的最小支配集，有贪心和 DP 两种方式。

贪心时，按 DFS 序倒序处理，能保证当前节点的子树除了根都已经被支配。如果这个节点未被支配，则有将当前节点或父节点加入支配集两种方式，显然后者更优。

P2899

#include<bits/stdc++.h>
using namespace std;
int n,ans;
bool vis1[10005],vis2[10005];
vector<int>e[10005];
void dfs(int pos,int fa1,int fa2){
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa1)dfs(e[pos][i],pos,fa1);
  if(!vis2[pos]){
    if(!vis1[fa1])vis1[fa1]=1,ans++;
    vis2[pos]=vis2[fa1]=vis2[fa2]=1;
  }
}
int main(){
  cin>>n;
  for(int i=1,u,v;i<n;i++)cin>>u>>v,e[u].push_back(v),e[v].push_back(u);
  return dfs(1,0,0),cout<<ans<<'\n',0;
}

拓展一下，假如一个点可以支配的距离大于一怎么做。显然的想法是改为在 \(k\) 级祖先上放点，这时会发现做法寄了。

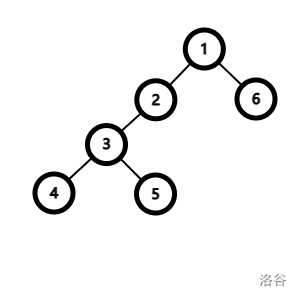
感性理解：假设支配距离为 \(2\)，答案为在 \(2\) 处放一个点。然而如果按上面的方式贪心的话，如果先搜 \(6\)，就会在 \(1\) 处放点而错误。这是由于当支配距离大于一，一个点的祖先可能不存在，最优解是被不是祖先的点支配。

正确做法是按深度从大到小排序。这样既保证了上面的性质，又避免了这种情况。

然而，暴力对点打标记可能会 T。

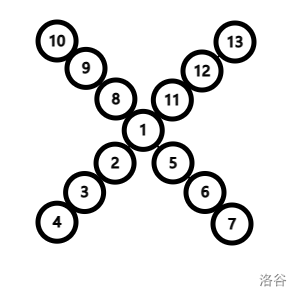
考虑一个菊花图挂了长为三的链。当支配距离为 \(2\)，会在 \(2\) 上放一个点，这时会对菊花周围一圈都打标记，退化为 \(O(n^2)\)。

维护一个 \(dis\) 表示到最近的支配点的距离。当枚举到一个节点时，用前 \(k\) 级祖先更新，如果距离大于 \(k\) 则在第 \(k\) 级祖先上放点。发现距离少了从子树转移的情况，更新 \(k\) 级祖先的前 \(k\) 级祖先的距离。

P3942

#include<bits/stdc++.h>
using namespace std;
int n,k,t,f[100005],dep[100005],p[100005],ans,dis[100005];
vector<int>e[100005];
bool cmp(int a,int b){
  return dep[a]>dep[b];
}
void dfs(int pos,int fa){
  f[pos]=fa,dep[pos]=dep[fa]+1;
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs(e[pos][i],pos);
}
int main(){
  memset(dis,0x3f3f3f3f,sizeof(dis)),cin>>n>>k>>t;
  for(int i=1;i<=n;i++)p[i]=i;
  for(int i=1,u,v;i<n;i++)cin>>u>>v,e[u].push_back(v),e[v].push_back(u);
  dfs(1,1),sort(p+1,p+n+1,cmp);
  for(int i=1;i<=n;i++){
    int now=p[i];
    for(int j=1;j<=k;j++)now=f[now],dis[p[i]]=min(dis[p[i]],dis[now]+j);
    if(dis[p[i]]>k){
      ans++;
      for(int j=0;j<=k;j++)dis[now]=min(dis[now],j),now=f[now];
    }
  }
  return cout<<ans<<'\n',0;
}

当点带权时，只能使用动态规划。设 \(f_{u,i}\) 表示支配以 \(u\) 为根的子树的最优解，\(i=0,1,2\) 分别表示 \(u\) 被自己、儿子、父亲支配。

当 \(u\) 被自己支配，儿子的三种情况都可以，即 \(f_{u,0}=\sum_{v\in son_u}\min(f_{v,0},f_{v,1},f_{v,2})\)。

当 \(u\) 被父亲支配，儿子不能也被父亲支配，即 \(f_{u,0}=\sum_{v\in son_u}\min(f_{v,0},f_{v,1},f_{v,2})\)。

当 \(u\) 被儿子支配，儿子可以被自己或儿子支配。当所有儿子都被儿子支配，就要选择其中一个儿子改成被自己支配，选择 \(f_{v,0}-f_{v,1}\) 最大的儿子加上。

P2458

#include<bits/stdc++.h>
using namespace std;
int n,f[1505][3];
vector<int>e[1505];
void dfs(int pos,int fa){
  int minn=0x3f3f3f3f;
  bool t=0;
  for(int i=0;i<e[pos].size();i++){
    if(e[pos][i]==fa)continue;
    dfs(e[pos][i],pos),f[pos][0]+=min(f[e[pos][i]][0],min(f[e[pos][i]][1],f[e[pos][i]][2])),f[pos][2]+=min(f[e[pos][i]][0],f[e[pos][i]][1]);
    if(f[e[pos][i]][0]<=f[e[pos][i]][1])f[pos][1]+=f[e[pos][i]][0],t=1;
    else f[pos][1]+=f[e[pos][i]][1],minn=min(minn,f[e[pos][i]][0]-f[e[pos][i]][1]);
  }
  if(!t)f[pos][1]+=minn;
}
int main(){
  cin>>n;
  for(int i=1,u,k,m;i<=n;i++){
    cin>>u>>k>>m,f[u][0]=k;
    for(int j=1,v;j<=m;j++)cin>>v,e[u].push_back(v),e[v].push_back(u);
  }
  return dfs(1,0),cout<<min(f[1][0],f[1][1])<<'\n',0;
}

同样可拓展到支配距离不为一的情况，把节点被 \(i\) 级儿子，自己和 \(i\) 级祖先支配的情况设出来即可。

点覆盖

一张无向图，如果一个点集使所有边的至少一个端点在点集中，则称这个点集是图的一个点覆盖。求一般图的最小点覆盖是 NP-hard 的。

二分图的最小点覆盖有一重要性质 König 定理：最小点覆盖等于最大匹配。

然后想树的最小点覆盖怎么做。如果将树按奇数和偶数深度分类，显然是二分图，跑最大匹配即可。然而这样的复杂度不够优秀。

DP 比较简单，且可以点带权。如果选当前节点，那么儿子有选和不选两种；否则儿子必须选。即 \(f_{u,0}=\sum_{v\in son_u}f_{v,1},f_{u,1}=\sum_{v\in son_u}\min(f_{v,0},f_{v,1})\)。

P2016

#include<bits/stdc++.h>
using namespace std;
int n,f[1505][2];
vector<int>e[1505];
void dfs(int pos,int fa){
  f[pos][1]=1;
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs(e[pos][i],pos),f[pos][0]+=f[e[pos][i]][1],f[pos][1]+=min(f[e[pos][i]][0],f[e[pos][i]][1]); 
}
int main(){
  cin>>n;
  for(int i=1,u,k;i<=n;i++){
    cin>>u>>k,u++;
    for(int j=1,v;j<=k;j++)cin>>v,v++,e[u].push_back(v),e[v].push_back(u);
  }
  return dfs(1,0),cout<<min(f[1][0],f[1][1])<<'\n',0;
}

贪心的方法与最小支配集类似，按 DFS 序逆序，若当前节点和父节点都不在点集中，就选择父节点。注意特判根节点。

#include<bits/stdc++.h>
using namespace std;
int n,ans;
bool vis[1505];
vector<int>e[1505];
void dfs(int pos,int fa){
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs(e[pos][i],pos);
  if(pos!=1&&!vis[pos]&&!vis[fa])ans++,vis[fa]=1;
}
int main(){
  cin>>n;
  for(int i=1,u,k;i<=n;i++){
    cin>>u>>k,u++;
    for(int j=1,v;j<=k;j++)cin>>v,v++,e[u].push_back(v),e[v].push_back(u);
  }
  return dfs(1,0),cout<<ans<<'\n',0;
}

独立集

一张无向图，选出一些点互不相邻，称为独立集。最大独立集大小记作 \(\alpha(G)\)。求一般图的最大独立集是 NP-hard 的。

在任意图中，一个点集是点覆盖的充要条件是补集为独立集。点覆盖的定义为所有边至少一个端点在点集中，则边至多一个端点在点集的补集中。同理可以反推。因此最小点覆盖的补集为最大独立集。最大权独立集同理。

[[图论]]