二分图最大匹配 学习笔记

基本概念

二分图是一种特殊的无向图。图的节点可以被分成两个部分，满足没有边连接相同的部分，记两个部分为左部点和右部点。

一张图的匹配，就是选出一些边没有公共顶点，最大匹配就是选出的边数最多。

增广路算法

增广路：

交错路始于非匹配点且由匹配边与非匹配边交错而成。

增广路是始于非匹配点且终于非匹配点的交错路。

举个例子：

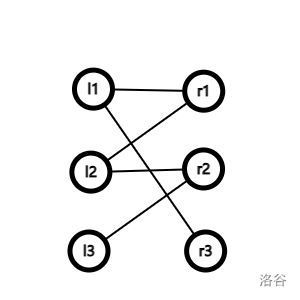
假设现在 \(l1,l2\) 分别配对 \(r1,r2\)。这时尝试将 \(l3\) 匹配到 \(r2\)。

这时 \(r2\) 的匹配对象 \(l2\) 就没有匹配了，因此对 \(l2\) 尝试匹配 \(r1\)。

同样的，\(r1\) 的匹配对象 \(l1\) 要重新匹配，刚好可以匹配到 \(r3\)，那么现在的匹配为 \(l1,l2,l3\) 配 \(r2,r3,r1\)。

观察上面重新匹配的过程，\(l3\to r2\to l2\to r1\to l1\to r3\) 为一条增广路。这条路径满足非匹配边与匹配边相间，且起点与终点未匹配，走这条路径会让匹配数加一。

增广路算法的思路就是枚举增广路的起点，dfs 找增广路。

代码：

bool vis[m+5];
bool dfs(int pos,vector<int>e[],int a[]){
  for(int i=0;i<e[pos].size();i++){
    if(!vis[e[pos][i]]){
      vis[e[pos][i]]=1;
      if(!a[e[pos][i]]||dfs(a[e[pos][i]],e,a))return a[e[pos][i]]=pos,1;
    }
  }
  return 0;
}
int match(int n,vector<int>e[],int a[],int ans=0){
  for(int i=1;i<=n;i++)memset(vis,0,sizeof(vis)),ans+=dfs(i,e,a);
  return ans;
}

结合代码来看：

\(a\) 表示匹配方案，\(a_i=j\) 表示第 \(i\) 个右部点配第 \(j\) 个左部点。枚举左部点作为增广路起点 dfs。

对于当前点，枚举出边。如果对应的右部点没有匹配，或者沿着这条边走可以增广，就更新匹配。

其中 \(vis\) 表示这个点是否被前面的点访问过，如果为真，说明前面的点尝试过走这个点增广，没必要重复尝试。由于枚举后匹配会被更新，因此要清空，或者对 \(vis\) 打时间戳。

复杂度 \(O(nm)\)。

相关定理

König 定理：最小点覆盖指选出最少的点使每条边都有端点被选。二分图最小点覆盖等于最大匹配。

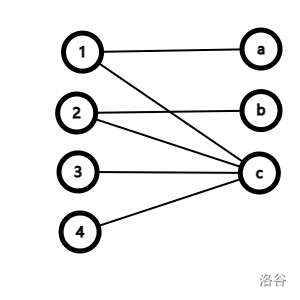
证明：构造一个方案。从二分图左侧所有未匹配点开始走交错路，最小点覆盖为左侧未被经过的点和右侧经过的点。比如图中最大匹配为 \(1\to a,2\to b,3\to c\)，从 \(4\) 走交错路 \(4\to c\to 3\)，最小点覆盖为 \(1,2,c\)。

引理 1：选出的点集覆盖所有边。

设有一条边未被覆盖，则左侧被经过，右侧未被经过。当这条边是匹配边，左端点被标记，右端点未被标记。如果这条边是非匹配边，则经过左端点的交错路可以继续走这条边到达右端点，矛盾；如果这条边是匹配边，则经过左端点的交错路一定从右端点来，因为一个点只有一条匹配边，矛盾。同理可得匹配边的两端不能同时在点集中。

引理 2：点集大小等于最大匹配数。

左边不能到达的点一定是匹配点，因为从左边非匹配点开始出发。如果右边的点是非匹配点，则经过右边的交错路的两端都是非匹配点，就成了增广路，与最大匹配矛盾。因此点集中的点为匹配点。由引理一可知每条匹配边有且仅有一个端点在点集中。

引理 3：选出的点集是最小点覆盖。

一条匹配边的两端至少选一个，因此最小点覆盖不小于最大匹配。

综上，二分图最小点覆盖等于最大匹配。

[[图论]]