线性代数相关

定义

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。

同型矩阵：行数和列数相同的两个矩阵。

方阵：行数等于列数的矩阵。

主对角线：方阵中行数等于列数的元素构成的对角线。

对角矩阵：主对角线之外的元素均为 $0$ 的方阵，记作 $\operatorname{diag}\{\lambda_1,\cdots,\lambda_n\}$。

单位矩阵：主对角线元素全为 $1$ 的对角矩阵，记作 $I$。

三角矩阵：上三角矩阵是主对角线左下方均为 $0$ 的方阵。下三角矩阵是主对角线右上方均为 $0$ 的方阵。

矩阵加减：同型的矩阵能相加或相减，结果是对应位置相减。

\[\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix}+\begin{bmatrix}1&9&1\\9&8&1\end{bmatrix}=\begin{bmatrix}2&10&5\\14&9&5\end{bmatrix} \]

\[\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix}-\begin{bmatrix}1&9&1\\9&8&1\end{bmatrix}=\begin{bmatrix}0&-8&3\\-4&-7&3\end{bmatrix} \]

数乘：一个数乘上一个矩阵，结果是一个矩阵，矩阵内的每一项都乘上这个数。

\[2\cdot\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix}=\begin{bmatrix}2&2&8\\10&2&8\end{bmatrix} \]

转置：将矩阵的行列交换。

\[\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix}^T=\begin{bmatrix}1&5\\1&1\\4&4\end{bmatrix} \]

共轭：矩阵的每个元素的虚部取反。

\[A=\begin{bmatrix}1+i&1+4i&5+i\\1+4i&1+9i&1+9i\end{bmatrix},\overline{A}=\begin{bmatrix}1-i&1-4i&5-i\\1-4i&1-9i&1-9i\end{bmatrix} \]

共轭转置：即取共轭，又取转置。

\[A=\begin{bmatrix}1+i&1+4i&5+i\\1+4i&1+9i&1+9i\end{bmatrix},\overline{A}=\begin{bmatrix}1-i&1-4i\\1-4i&1-9i\\5-i&1-9i\end{bmatrix} \]

矩阵乘法：要求第一个矩阵的列数与第二个矩阵的列数相同，有 $(AB)_{i,j}=\sum_{k=1}^p A_{i,k}B_{k,j}$。即新矩阵的元素等于所在第一个矩阵上的行和第二个矩阵上的列上的每个元素对应相乘的和。单位矩阵是矩阵乘法的单位元。矩阵乘法有结合律，对加法的分配律，没有交换律。

\[\begin{aligned}\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix}\begin{bmatrix}1&9\\9&8\\1&1\end{bmatrix}&=\begin{bmatrix}1\times1+1\times9+4\times1&1\times9+1\times8+4\times1\\5\times1+1\times9+4\times1&5\times9+1\times8+4\times1\end{bmatrix}\\&=\begin{bmatrix}14&21\\18&57\end{bmatrix}\end{aligned} \]

矩阵求逆：对于方阵 $A$，$A$ 的逆矩阵为 $A^{-1}$，满足 $AA^{-1}=I$。

行列式：行列式是方阵的一种运算，记作 $\det A$。其定义为：

\[\det A=\sum_p(-1)^{\tau(p)}\prod_{i=1}^n A_{i,p_i} \]

其中 $p$ 是一个排列，$\tau$ 表示逆序对数。相当于选出 $n$ 个行列互不相同的元素，对乘积求和，系数是列数的逆序对。

矩阵的初等变换：有三种操作：将一行/列乘 $k$、交换两行/列、将一行/列的若干倍加到另一行/列上。以下简称为倍乘、对换、倍加。

矩阵加速递推

已知一个数列 $a$，满足 $a_x=\begin{cases}1 & x \in\{1,2,3\}\\ a_{x-1}+a_{x-3} & x \geq 4\end{cases}$。

如果直接递推计算是 $O(n)$ 的，但是运用矩阵乘法可以加速到 $O(\log n)$。

构造一个矩阵 $\begin{bmatrix}a_{i+1}&a_i&a_{i-1}\end{bmatrix}$；

把上面的递推式代入：$\begin{bmatrix}a_i+a_{i-2}&a_i&a_{i-1}\end{bmatrix}$；

补充成一个好看的形式：$\begin{bmatrix}1\times a_i+0\times a_{i-1}+1\times a_{i-2}&1\times a_i+0\times a_{i-1}+0\times 0_{i-2}&0\times a_i+1\times a_{i-1}+0\times a_{i-2}\end{bmatrix}$

这时，可以发现矩阵变成了一个矩阵乘法的形式，即 $\begin{bmatrix}a_i&a_{i-1}&a_{i-2}\end{bmatrix}\begin{bmatrix}1&0&1\\1&0&0\\0&1&0\end{bmatrix}$。

那么矩阵 $\begin{bmatrix}1&0&1\\1&0&0\\0&1&0\end{bmatrix}$ 就是转移矩阵。已知 $\begin{bmatrix}a_3&a_2&a_1\end{bmatrix}$，乘上转移矩阵的 $n-2$ 次方就能得到 $\begin{bmatrix}a_{n}&a_{n-1}&a_{n-2}\end{bmatrix}$。

矩阵乘法满足结合律，那么重载一下运算符就可以直接使用快速幂。复杂度 $O(|T|^3\log n)$。这题里 $T=3$，可以看作 $\log n$ 带一个 $27$ 倍的常数。

如果涉及到加常数，可以在矩阵中多加一维常数维。

矩阵加速图上问题

定长路径统计

有这样一类问题：一个图，给定起点和终点，问长度为 $t$ 的路径有几条。

首先建出邻接矩阵 $dis$，表示长度为 $1$ 的路径的个数。如果要转移到 $dis'$ 表示长度为 $1$ 的路径的个数。通过加法原理和乘法原理可以得到 $dis'_{i,j}=\sum_{k=1}^n dis_{i,k}dis_{k,j}$。

回顾矩阵乘法 $(AB)_{i,j}=\sum_{k=1}^p A_{i,k}B_{k,j}$，发现上面的转移就是矩阵乘法，直接把邻接矩阵取 $t$ 次幂。

例题：

P3758

自爆：建一个超级汇点，其他点向这个点连边，只进不出；

停在原地：每个点（包括超级汇点）连一个自环。

P2233

到达 E 后不再换车：删除 E 的出边。

P2151

把原图的边看作点建一个新图，两个点连有向边仅当一条边的终点是另一条边的起点。不会立刻沿着刚刚走来的路走回即相反边之间不连边。

定长最短路

P2886

朴素的转移：$dis'_{i,j}=\min_{i=1}^n(dis_{i,k}+dis_{k,j})$

这很像上面的矩阵乘法，定义一个新的运算 $(A\operatorname{opt}B)_{i,j}=\min_{i=1}^n(dis_{i,k}+dis_{k,j})$。

这个运算满足结合律，也可以使用快速幂。离散化一下，复杂度 $O(T^3\log N)$。

矩阵表示修改

在数据结构中如果有一些复杂的加、乘等操作，可以用矩阵表示修改。

P7453

发现第一类操作不是正常线段树可做的，第二类操作也麻烦。考虑用矩阵表示修改。因为有常数，所以矩阵为 $\begin{bmatrix}a&b&c&1\end{bmatrix}$。可以构造出六个矩阵：

\[\begin{bmatrix}1&0&0&0\\1&1&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix} \]

\[\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&1&1&0\\0&0&0&1\\\end{bmatrix} \]

\[\begin{bmatrix}1&0&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix} \]

\[\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\v&0&0&1\\\end{bmatrix} \]

\[\begin{bmatrix}1&0&0&0\\0&v&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix} \]

\[\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&v&1\\\end{bmatrix} \]

然后维护矩阵的和。因为矩阵乘法对矩阵加法有分配律，所以这和在叶子结点操作后加起来是一样的。

高斯消元

消元就是将矩阵通过初等变换，化成特殊的矩阵。高斯消元就是消成上三角矩阵。高斯消元可求解形如 $\begin{cases} a_{1, 1} x_1 + a_{1, 2} x_2 + \cdots + a_{1, n} x_n = b_1\\ a_{2, 1} x_1 + a_{2, 2} x_2 + \cdots + a_{2, n} x_n = b_2 \\ \cdots \\ a_{n,1} x_1 + a_{n, 2} x_2 + \cdots+ a_{n, n} x_n = b_n \end{cases}$
的线性方程组。

将 $b$ 放到 $a$ 的右边，构成一个 $n$ 行 $n+1$ 列的矩阵，称为线性方程组的增广矩阵。

枚举当前的方程组 $r$，未知数 $c$。首先将 $x_c$ 最大的一行换到当前行，这一步是为了减少误差。此时若 $a_{r,c}=0$，跳过这个未知数。然后枚举 $a_{j,c}(r\leq j\leq n)$，将这个未知数减到 $0$。

由于存在无解和多解，最后的矩阵去掉最后一列不一定是对角矩阵，可能几行和几列为 $0$。如果 $r<n$（根据实现方式可能减一），就说明有的方程可以被其他方程消掉，是无效的，此时无解或多解。枚举 $r+1\sim n$，这几行的 $1\sim n$ 列都为 $0$。最后一列不为 $0$ 则无解，否则多解。

此时一定有解，且 $a_{i,i}=1$。那么这就知道了 $x_n$，带入到第 $n-1$ 行可以解出 $x_{n-1}$，类似地不断回代就可以解出。复杂度 $O(n^3)$。

#include<bits/stdc++.h>
using namespace std;
int n;
double a[105][105];
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)for(int j=1;j<=n+1;j++)cin>>a[i][j];
  int r=1;
  for(int c=1;c<=n;c++){
    int pos=r;
    for(int i=r;i<=n;i++)if(fabs(a[pos][c])<fabs(a[i][c]))pos=i;
    if(fabs(a[pos][c])<1e-8)continue;
    swap(a[r],a[pos]);
    for(int i=n+1;i>=c;i--)a[r][i]/=a[r][c];
    for(int i=r+1;i<=n;i++)for(int j=n+1;j>=c;j--)a[i][j]-=a[r][j]*a[i][c];
    r++;
  }
  if(--r<n){
    for(int i=r+1;i<=n;i++)if(fabs(a[i][n+1])>1e-8)return puts("-1"),0;
    return puts("0"),0;
  }
  for(int i=n-1;i>=1;i--)for(int j=i+1;j<=n;j++)a[i][n+1]-=a[j][n+1]*a[i][j];
  for(int i=1;i<=n;i++)cout<<setprecision(2)<<fixed<<'x'<<i<<'='<<a[i][n+1]<<'\n';
  return 0;
}

高斯消元还可以求解异或方程组，此时消元直接异或即可。可以 bitset 优化，$O(\frac{n^3}w)$。

行列式求值

回顾行列式的定义：$\det A=\sum_p(-1)^{\tau(p)}\prod_{i=1}^n a_{i,p_i}$。这个式子无法直接做。

对于上三角矩阵，行列式就是主对角线上元素的积，因为排列只有 $1\sim n$ 一种，其他都为 $0$。可以考虑将矩阵消成上三角矩阵后反推出行列式。

分析一下行列式的性质。

定理一：$\det A=\det A^T$。定义一个排列 $p$ 的逆排列为 $p'$，$p'_{p_i}=i$。显然排列和逆排列的逆序对数相等。则转置后相当于枚举逆排列，结果不变。

定理二：倍乘 $k$，则对于每个排列，后面的乘积乘 $k$，行列式也乘 $k$；

定理三：对换，相当于交换了所有排列的两项，逆序对数的奇偶性变了，行列式变号；

定理四：若矩阵的两行有倍数关系，则行列式为 $0$。先扩倍成相同的两行，因为交换这两行不改变矩阵，则 $\det A=-\det A,\det A=0$。（类似，只要几行线性相关，行列式就为 $0$）。

定理五：倍加 $k$，行列式不变。设第 $a$ 行的 $k$ 倍加到第 $b$ 行上，$A$ 为原矩阵，$C$ 为变化后的矩阵，构造 $B$，除了 $B$ 的第 $b$ 行为第 $a$ 行的 $k$ 倍，其他部分与 $A$ 相同。根据定理三有 $\det B=0$。但是发现对于每个排列，$C$ 的第 $b$ 行都是 $A,B$ 的和，所以 $\det C=\det A+\det B,\det A=\det C$。

定理六：列初等变换也有同样的结论，相当于转置之后的行。

因此，我们可以高斯消元求行列式。

P7112

模板题。有一个问题就是模数不是质数，所以不能除。我们可以对两行进行辗转相除，这样不需要求逆元。

#include<bits/stdc++.h>
using namespace std;
char buf1[2097152],*ip1=buf1,*ip2=buf1;
inline int getc(){
  return ip1==ip2&&(ip2=(ip1=buf1)+fread(buf1,1,2097152,stdin),ip1==ip2)?EOF:*ip1++;
}
template<typename T>void in(T &a){
  T ans=0;
  char c=getc();
  for(;c<'0'||c>'9';c=getc());
  for(;c>='0'&&c<='9';c=getc())ans=ans*10+c-'0';
  a=ans;
}
template<typename T,typename... Args>void in(T &a,Args&...args){
  in(a),in(args...);
}
int n,mod,a[605][605],ans=1;
int main(){
  in(n,mod);
  for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)in(a[i][j]),a[i][j]%=mod;
  for(int i=1;i<=n;i++){
    for(int j=i+1,t;j<=n;j++){
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++)a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)ans=1ll*ans*a[i][i]%mod;
  return cout<<(ans+mod)%mod<<'\n',0;
}

考虑证一下复杂度。对于每行，每次辗转相除，要么 $a_{i,i}$ 不变，此时只需要一次辗转相除就可以消元一行，要么减半。因此每行的辗转相除只会做 $O(n+\log V)$ 次，复杂度 $O(n^3+n^2\log V)$。

如果用辗转相除求逆元，是不需要把下面的行换上来的，因为辗转相除会自己交换。但是直接求逆需要将下面不为 $0$ 的行换上来。

矩阵求逆

三个初等变换，其实相当于左乘一个矩阵。

倍乘矩阵：$\operatorname{diag}\{1,\cdots,1,k,1,\cdots,1\}$。设倍乘第 $i$ 行，则 $k$ 在第 $i$ 行。

对换矩阵：$\begin{bmatrix}I_{i-1} & & & & \\ & 0 & & 1 & \\ & & I_{j-i-1} & & \\ & 1 & & 0 & \\ & & & & I_{n-j}\\\end{bmatrix}$。设对换第 $i,j$ 行，则在 $I$ 的基础上将 $a_{i,i},a_{j,j}$ 改为 $0$，$a_{i,j},a_{j,i}$ 改为 $1$。

倍加矩阵：$\begin{bmatrix}1 & & & & & & \\ & \ddots & & & & & \\ & & 1 & \cdots & k & & \\ & & & \ddots & \vdots & & \\ & & & & 1 & & \\ & & & & & \ddots & \\ & & & & & & 1\\\end{bmatrix}$。设将第 $i$ 行的 $k$ 倍加到第 $j$ 行，则在 $I$ 的基础上将 $a_{i,j}$ 改为 $k$。

然后看矩阵求逆。因为 $A^{-1}A=I,A^{-1}I=A^{-1}$，因此我们将 $A$ 消成 $I$ 就是对 $A$ 乘上了 $A^{-1}$，此时只要对 $I$ 进行相同的变换就得到了 $A^{-1}$。如果中途出现了整列为空，说明消不成单位矩阵，无解。

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
int n,a[405][805];
template<typename T>T qpow(T a,T b,T n,T ans=1){
  for(a%=n;b;b>>=1)b&1&&(ans=1ll*ans*a%n),a=1ll*a*a%n;
  return ans;
}
template<typename T>T inv(T a,T b)
{
  return qpow(a,b-2,b);
}
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>a[i][j];
  for(int i=1;i<=n;i++)a[i][n+i]=1;
  for(int i=1;i<=n;i++){
    int pos=i;
    while(pos<=n&&!a[pos][i])pos++;
    if(pos>n)return puts("No Solution"),0;
    swap(a[i],a[pos]);
    int temp=inv(a[i][i],mod);
    for(int j=1;j<=2*n;j++)a[i][j]=1ll*a[i][j]*temp%mod;
    for(int j=1;j<=n;j++)if(j!=i)for(int k=2*n;k>=i;k--)a[j][k]=(a[j][k]-1ll*a[j][i]*a[i][k]%mod+mod)%mod;
  }
  for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cout<<a[i][j+n]<<(j==n?'\n':' ');
  return 0;
}

LGV 引理

LGV 引理可以数 DAG 上的不相交路径。

一组 $A\to B$ 的不相交路径 $S$ 是 $n$ 条没有公共顶点的路径，起点集合为 $A$，终点集合为 $B$，大小都为 $n$，$S_i$ 是一条 $A_i\to B_{p_i}$ 的路径，$p$ 是一个排列。

记 $P$ 是一条路径，$\omega(P)$ 为 $P$ 上所有边的边权之积，$e(u,v)$ 表示 $u\to v$ 的所有路径的 $\omega$ 之和。定义矩阵 $M$ 满足 $M_{i,j}=e(i,j)$，则有：

\[\sum_{S:A\to B}(-1)^{\tau(p)}\prod_{i=1}^n\omega(S_i)=\det M \]

证明一下，展开 $\det M$：

\[\begin{aligned}\det M&=\sum_p(-1)^{\tau(p)}\prod_{i=1}^n A_{i,p_i}\\&=\sum_{p}(-1)^{\tau(p)}\prod_{i=1}^ne(A_i,B_{p_i})\end{aligned} \]

$e$ 是 $i\to j$ 的全部路径的边权积的和，因此我们发现这个式子实际上在数 $A\to B$ 的全部路径。那么相差的就是相交路径，只需要证明相交路径组的和为 $0$。

考虑将相交路径组配对。找到路径上有交点的最小的 $i$，再找到与 $P_i$ 相交且交点离 $A_i$ 最近的 $j$ 中最小的 $j$，然后将两条路径的第一个交点之后的部分互换。这样得到一个新的路径组，它的贡献符号相反，而且再次交换时 $i,j$ 不变。

有一种伪证是交换最小的有交点的 $(i,j)$。考虑下面的图：

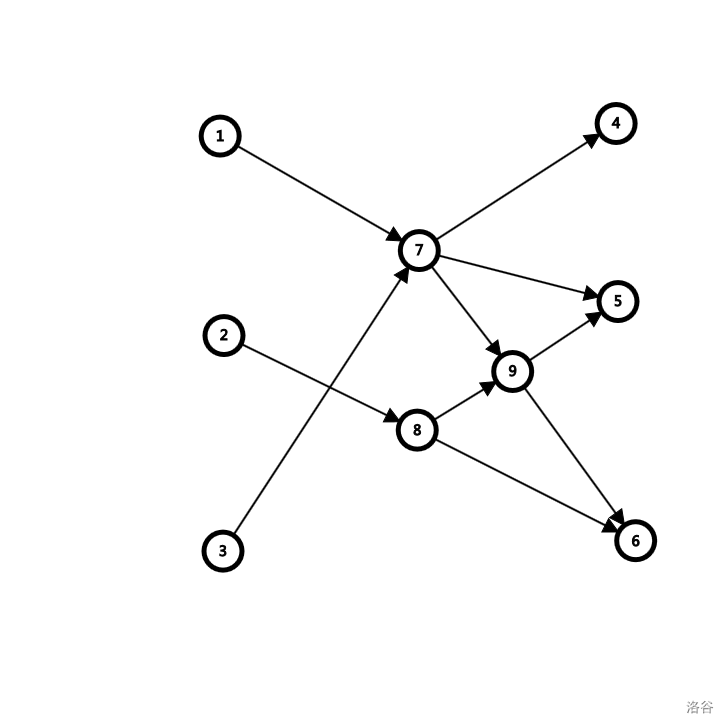
原来的路径组为 $1\to7\to4,2\to8\to9\to5,3\to7\to9\to6$，交换后变为 $1\to7\to9\to6,2\to8\to9\to5,3\to7\to4$。但是再交换后变成了 $1\to7\to9\to5,2\to8\to9\to6,3\to7\to4$。

问题在于交换后最小的 $j$ 可能变化，关键在于找到一个不动点。因为只交换交点后的部分，新的交点只会产生在第一个交点之后，所以第一个交点不变。那么经过这个点的最小的 $j$ 也不变，得证。

P6657

模版题。

注意到这是在网格上走，所以合法的 $p$ 只有 $1\sim n$。因此方案数就为 $\det M$。$e(i,j)$ 可以用组合数计算。

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
int t,n,m,fac[2000005],vac[2000005],a[105],b[105],c[105][105];
template<typename T>T qpow(T a,T b,T n,T ans=1){
  for(a%=n;b;b>>=1)b&1&&(ans=1ll*ans*a%n),a=1ll*a*a%n;
  return ans;
}
template<typename T>T inv(T a,T b)
{
  return qpow(a,b-2,b);
}
template<int maxn>int det(int n,int a[maxn][maxn],int ans=1){
  for(int i=1;i<=n;i++){
    for(int j=i+1,t;j<=n;j++){
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++)a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)ans=1ll*ans*a[i][i]%mod;
  return (ans+mod)%mod;
}
int main(){
  fac[0]=1;
  for(int i=1;i<=2000000;i++)fac[i]=1ll*fac[i-1]*i%mod;
  vac[0]=1,vac[2000000]=inv(fac[2000000],mod);
  for(int i=1999999;i>=1;i--)vac[i]=1ll*vac[i+1]*(i+1)%mod;
  cin>>t;
  while(t--){
    cin>>n>>m;
    for(int i=1;i<=m;i++)cin>>a[i]>>b[i];
    for(int i=1;i<=m;i++)for(int j=1;j<=m;j++)c[i][j]=a[i]<=b[j]?1ll*fac[b[j]-a[i]+n-1]*vac[b[j]-a[i]]%mod*vac[n-1]%mod:0;
    cout<<det(m,c)<<'\n';
  }
  return 0;
}

CF438D

可以转化为不相交路径，起点为 $(1,2),(2,1)$，终点为 $(n-1,m),(n,m-1)$。根据 LGV 引理，答案为 $f(1,2,n-1,m)f(2,1,n,m-1)-f(1,2,n,m-1)f(1,2,n-1,m)$，$f$ 为两点间路径数，可以 DP。

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
int n,m,f[3005][3005];
char s[3005][3005];
int solve(int a,int b,int c,int d){
  memset(f,0,sizeof(f)),f[a][b]=1;
  for(int i=a;i<=n;i++)for(int j=b;j<=m;j++)f[i][j]=s[i][j]=='.'?(f[i][j]+(f[i-1][j]+f[i][j-1])%mod)%mod:0;
  return f[c][d];
}
int main(){
  cin>>n>>m;
  for(int i=1;i<=n;i++)scanf("%s",s[i]+1);
  return cout<<(1ll*solve(1,2,n-1,m)*solve(2,1,n,m-1)%mod-1ll*solve(1,2,n,m-1)*solve(2,1,n-1,m)%mod+mod)%mod<<'\n',0;
}

P7736

首先，一个路径方案的交点数就是 $\tau(p)$。对于两条路径，每在中途交换一次，相当于交换了两条路径的先后，逆序对个数和交点数的奇偶性都变化。

则题目要求的偶数个交点的路径方案数比有奇数个交点的路径方案数多多少个就是 $\sum_{S:A\to B}(-1)^{\tau(p)}\prod_{i=1}^n\omega(S_i)$，求出 $\det M$ 即可。

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
int t,k,n[105],m[105],f[205][105][2],a[105][105];
template<int maxn>int det(int n,int a[maxn][maxn],int ans=1){
  for(int i=1;i<=n;i++){
    for(int j=i+1,t;j<=n;j++){
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++)a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)ans=1ll*ans*a[i][i]%mod;
  return (ans+mod)%mod;
}
int main(){
  cin>>t;
  while(t--){
    cin>>k;
    for(int i=1;i<=k;i++)cin>>n[i];
    for(int i=1;i<k;i++)cin>>m[i];
    for(int i=1;i<=n[1];i++)f[i][i][0]=1;
    for(int i=1;i<k;i++){
      for(int j=1;j<=n[i+1];j++)for(int k=1;k<=n[1];k++)f[j][k][i&1]=0;
      for(int j=1,u,v;j<=m[i];j++){
        cin>>u>>v;
        for(int k=1;k<=n[1];k++)f[v][k][i&1]=(f[v][k][i&1]+f[u][k][~i&1])%mod;
      }
    }
    for(int i=1;i<=n[1];i++)for(int j=1;j<=n[k];j++)a[i][j]=f[j][i][~k&1];
    cout<<det(n[1],a)<<'\n',memset(f,0,sizeof(f));
  }
  return 0;
}

矩阵树定理

矩阵树定理可用于数图的生成树。

无向图形式：定义无向图 $G$ 的拉普拉斯矩阵 $L(G)$ 为 $L(G)=\begin{cases}deg_i,\,&i=j\\-m_{i,j},\,&i\ne j\end{cases}$，其中 $m_{i,j}$ 为 $i,j$ 之间的边数，$t(G)$ 为 $G$ 的生成树个数，$L_0(G)$ 去掉为 $G$ 第 $i$ 行和第 $i$ 列的矩阵，此处 $i$ 是任意的。则有：

\[t(G)=\det L_0(G) \]

证明：

定义图的关联矩阵 $M$，$M$ 是一个 $n\times m$ 的矩阵，$n,m$ 分别为 $G$ 的点数和边数。对边随意定一个向。当 $i$ 是第 $j$ 条边的起点，$M_{i,j}=1$；当 $i$ 是第 $j$ 条边的终点，$M_{i,j}=-1$。其他位置为 $0$。

引理一：$MM^T=L$。

$(MM^T)_{i,j}=\sum_{k=1}^m M_{i,k}M^T_{k,j}=\sum_{k=1}^m M_{i,k}M_{j,k}$。当 $i=j$，当 $i$ 与边 $k$ 相连时贡献 $1$，总共 $deg_i$；否则当 $i,j$ 与边 $k$ 都相连时贡献 $-1$，总共 $m_{i,j}$。

定义图的减关联矩阵 $M_0$ 为 $M$ 去掉任意一行（与 $L_0$ 去掉的相同）后的矩阵。类似可以证明 $M_0M_0^T=L$。若 $S$ 是一个大小为 $n-1$ 且元素都是不大于 $m$ 的正整数的集合，定义图的子减关联矩阵 $M_0[S]$ 为取出 $M_0$ 中 $S$ 对应的列构成的矩阵。

引理二：若 $S$ 对应的边集构成生成树，则 $\det M_0[S]=\pm1$，否则 $\det M_0[S]=0$。

若 $S$ 不构成生成树，则一定有环。将环对应的几列相加，有值的位置可以全部抵消，因此这几列线性相关，行列式为 $0$。

若 $S$ 构成生成树，假设去掉的行列对应的节点为根，将矩阵的行按照深度从大到小排序，列排序后第 $i$ 列对应的边为节点 $i$ 连向父亲的边。这样排完后成了下三角矩阵，且对角线上都有值，积为 $\pm 1$。

然后还需要用到 Binet−Cauchy 定理：若 $A,B$ 分别为 $n\times m,m\times n$ 的矩阵，则 $\det AB=\sum_S\det A[S]\det B[S]$。

有一个巧妙的证明。构造一个 DAG：

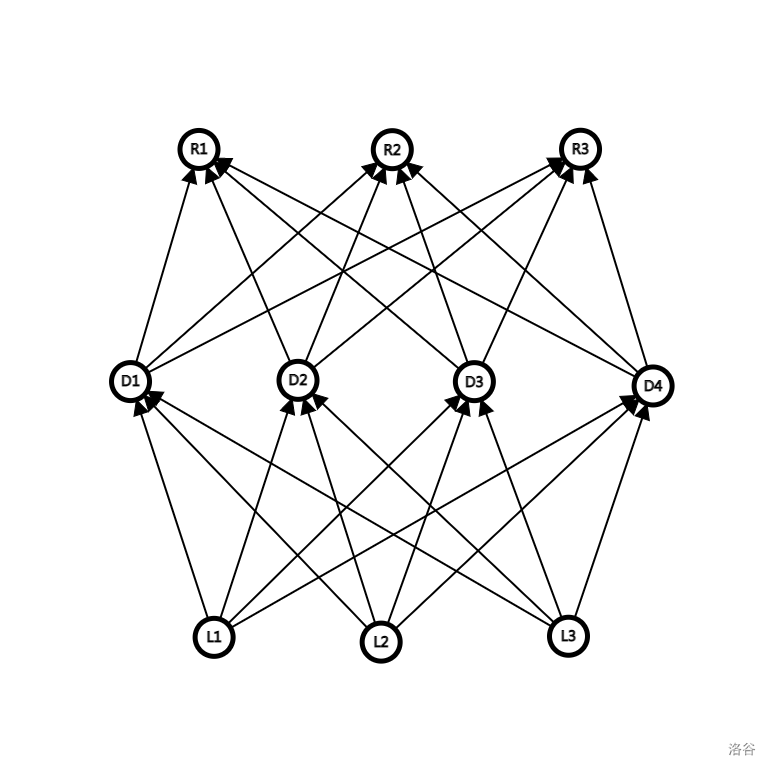
图有三个点集 $L,D,R$，大小分别为 $n,m,n$，$w(L_i,D_j)=a_{i,j},w(R_j,D_i)=B_{i,j}$。

使用 LGV 引理。等号左边，$(AB)_{i,j}=\sum_{k=1}^m a_{i,k}b_{k,j}$。这实际上就是枚举中转点计算 $e(i,j)$。实际意义就是计算 $L$ 到 $R$ 的不相交路径组中逆序对个数为偶数的权值和减去逆序对个数为奇数的权值和。

等号右边相当于枚举中转的 $D$，分别计算前半段乘后半段。展开后是前半段偶数×后半段偶数+前半段奇数×后半段奇数-前半段偶数×后半段奇数+前半段奇数×后半段偶数，也就等于整段偶数减整段奇数，得证。这也说明 $\det AB=\det A\det B$。

最终的证明：

\[\begin{aligned}\det L_0&=\det M_0M_0^T\\&=\sum_S \det M_0[S]\det M_0^T[S]\\&=\sum_S \det M_0[S]^2\text{(转置前后行列式相等)}\\&=t(G)\end{aligned} \]

矩阵树定理也有有向图的拓展。定义有向图 $G$ 的出度拉普拉斯矩阵 $L_{out}(G)$ 为 $L_{out}(G)=\begin{cases}out_i,\,&i=j\\-m_{i,j},\,&i\ne j\end{cases}$，入度拉普拉斯矩阵 $L_{in}(G)$ 为 $L_{in}(G)=\begin{cases}in_i,\,&i=j\\-m_{i,j},\,&i\ne j\end{cases}$，其中 $m_{i,j}$ 为 $i$ 指向 $j$ 的边数，$t^{root}(G,k)$ 为 $G$ 的以 $k$ 为根的根向树形图个数，$t^{leaf}(G,k)$ 为 $G$ 的以 $k$ 为根的叶向树形图个数，则有：

\[t^{root}(G,k)=\det L_0^{out}(G),t^{leaf}(G,k)=\det L_0^{in}(G) \]

$L_0^{root}(G),L_0^{leaf}(G)$ 分别为 $L^{root}(G),L^{leaf}(G)$ 去掉第 $k$ 行第 $k$ 列的矩阵。

证明考虑构造第二个关联矩阵 $M'$，假设是根向树形图，当 $i$ 为第 $j$ 条边的起点时 $M'_{i,j}=1$，其他位置为 $0$。则 $M'M^T=L_{out}$。类似可以证明当 $S$ 为生成树，$\det M'\det M=1$，否则为 $0$。

假如把重边数当做边权，结果可以看作所有生成树边权积的和。边权可以是抽象的东西，比如多项式、生成函数等。

P4336

$n$ 很小，可以 $2^n$ 枚举。枚举哪几个公司修，容斥即可。

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
int n,m[21],tu[21][141],tv[21][141],a[21][21],ans;
template<int maxn>int det(int n,int a[maxn][maxn],int ans=1){
  for(int i=1;i<=n;i++){
    for(int j=i+1,t;j<=n;j++){
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++)a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)ans=1ll*ans*a[i][i]%mod;
  return (ans+mod)%mod;
}
int main(){
  cin>>n;
  for(int i=1;i<n;i++){
    cin>>m[i];
    for(int j=1;j<=m[i];j++)cin>>tu[i][j]>>tv[i][j];
  }
  for(int i=0;i<1<<(n-1);i++){
    memset(a,0,sizeof(a));
    for(int j=0;j<n-1;j++){
      if(i>>j&1){
        for(int k=1;k<=m[j+1];k++){
          int u=tu[j+1][k],v=tv[j+1][k];
          a[u][u]=(a[u][u]+1)%mod,a[v][v]=(a[v][v]+1)%mod,a[u][v]=(a[u][v]-1+mod)%mod,a[v][u]=(a[v][u]-1+mod)%mod;
        }
      }
    }
    ans=(ans+1ll*det(n-1,a)*((n-1-__builtin_popcount(i))&1?mod-1:1)%mod+mod)%mod;
  }
  return cout<<ans<<'\n',0;
}

P2144

可以直接写出拉普拉斯矩阵：

\[\begin{bmatrix}n&-1&-1&-1&-1&\cdots&-1&-1\\-1&3&-1&0&0&\cdots&0&-1\\-1&-1&3&-1&0&\cdots&0&0\\-1&0&-1&3&-1&\cdots&0&0\\-1&0&0&-1&3&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\-1&0&0&0&0&\cdots&3&-1\\-1&-1&0&0&0&\cdots&-1&3\\\end{bmatrix} \]

去掉特殊的第一行第一列：

\[\begin{bmatrix}3&-1&0&0&\cdots&0&-1\\-1&3&-1&0&\cdots&0&0\\0&-1&3&-1&\cdots&0&0\\0&0&-1&3&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&3&-1\\-1&0&0&0&\cdots&-1&3\\\end{bmatrix} \]

将第一行交换到最后一行，行列式乘 $(-1)^n$：

\[\begin{bmatrix}-1&3&-1&0&\cdots&0&0\\0&-1&3&-1&\cdots&0&0\\0&0&-1&3&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&3&-1\\-1&0&0&0&\cdots&-1&3\\3&-1&0&0&\cdots&0&-1\\\end{bmatrix} \]

然后用 $1\sim n-3$ 行依次消最后两行。

对于倒数第二行，令每次消元相邻两个有值的位置为 $f$，则 $f_1=-1,f_2=0,f_{2i+1}=3f_{2i-1}+f_{2i},f_{2i+2}=-f_{2i-1}$。观察得到 $f_{2i+1}=-F_{2i+2},f_{2i+2}=F_{2i}$，其中 $F$ 为斐波那契数列。因此消完后最后两列分别为 $-f_{2n-2}-1,f_{2n-4}+3$。同理可得最后一行的最后两列为 $f_{2n},-f_{2n-2}-1$。

此时可以手算出行列式为 $(F_{2n-4}+3)F_{2n}-(F_{2n-2}+1)^2$，化简得 $F_{2n-1}+F_{2n+1}-2$。

#include<bits/stdc++.h>
using namespace std;
int n;
bign f[205];
int main(){
  f[1]=1,cin>>n;
  for(int i=2;i<=2*n+1;i++)f[i]=f[i-1]+f[i-2];
  return cout<<f[2*n-1]+f[2*n+1]-2<<'\n',0;
}

P3317

一个生成树的概率是生成树的边出现的概率乘其他边不出现的概率，也就是 $\sum_{T}\prod_{e\in T}p_e\prod_{e\notin T}(1-p_e)$。

将其他边变成所有边去掉树上的边，变成 $\prod_{e}(1-p_e)\sum_T\prod_{e\in T}\frac{p_e}{1-p_e}$，这个式子可以矩阵树。

对于 $p_e=1$，将 $p_e$ 减去一个极小值，误差可以接受。

#include<bits/stdc++.h>
using namespace std;
int n;
double a[55][55],p=1;
template<int maxn>double det(int n,double a[maxn][maxn],double ans=1){
  for(int i=1;i<=n;i++){
    int pos=i;
    for(int j=i;j<=n;j++)if(fabs(a[pos][i])<fabs(a[j][i]))pos=j;
    if(i!=pos)swap(a[i],a[pos]),ans*=-1;
    for(int j=i+1;j<=n;j++){
      if(i==j)continue;
      for(int k=n;k>=i;k--)a[j][k]-=a[i][k]*a[j][i]/a[i][i];
    }
  }
  for(int i=1;i<=n;i++)ans*=a[i][i];
  return ans;
}
int main(){
  cin>>n;
  for(int i=1;i<=n;i++){
    for(int j=1;j<=n;j++){
      cin>>a[i][j];
      if(a[i][j]>1-1e-8)a[i][j]-=1e-8;
      if(i<j)p*=1-a[i][j];
      a[i][j]/=1-a[i][j];
    }
  }
  for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(i!=j)a[i][i]+=a[i][j],a[i][j]=-a[i][j];
  return cout<<setprecision(12)<<fixed<<p*det(n-1,a)<<'\n',0;
}

P6624

首先反演。

\[\begin{aligned}\sum_{T}\sum_{e\in T}w_e\gcd_{e\in T}w_e&=\sum_{T}\sum_{e\in T}w_e\sum_{d\mid\gcd_{e\in T}w_e}\varphi(d)\text{($\varphi\ast\mathbf{1}=\operatorname{Id}$)}\\&=\sum_{d=1}^V\varphi(d)\sum_{T,d\mid\gcd_{e\in T}w_e}\sum_{e\in T}w_e\end{aligned} \]

枚举 $d$，将边权为 $d$ 的倍数的边加入图中。问题在于求生成树的边权和的和。

矩阵树定理求的是边权积的和。考虑怎样将乘法变成加法：设边权为一个一次函数 $w_ix+1$，两个函数相乘后边权就相加了。最后行列式的一次项为答案。

此时的复杂度为 $O(n^3V)$。加一个剪枝，边数小于 $n-1$ 的跳过。此时跑矩阵树的次数最多为 $\frac{\sum_{i=1}^m{d(w_i)}}{n-1}$ 也就是 $O(nd(V))$，复杂度优化为 $O(n^4d(V))$。

说一下一次函数的四则运算问题。我们不关心次数大于一的项。加减乘是容易的。除法涉及到求逆，设 $ax+b$ 的逆元为 $cx+d$，则有 $bd=1,ad+bc=0$，解得 $c=-\frac{a}{b^2},d=\frac 1 b$。

这又有一个问题，常数项为 $0$ 的求不了逆。每次消元，先枚举下面的行，将常数项不为 $0$ 的行换上来。如果没有，说明整列的常数项都为 $0$，此时要优先将一次项不为 $0$ 的行换上来，当成一个数消元。

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,m,maxn,prime[152506],phi[152506],ans;
bool vis[152506];
struct edge{
  int u,v,w;
}e[440];
template<typename T>T qpow(T a,T b,T n,T ans=1){
  for(a%=n;b;b>>=1)b&1&&(ans=1ll*ans*a%n),a=1ll*a*a%n;
  return ans;
}
template<typename T>T inv(T a,T b)
{
  return qpow(a,b-2,b);
}
int phi_init(int n,int prime[],int phi[],bool a[],int cnt=0){
  phi[1]=1;
  for(int i=2;i<=n;i++)a[i]=1;
  for(int i=2;i<=n;i++){
    if(a[i])prime[++cnt]=i,phi[i]=i-1;
    for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
      a[i*prime[j]]=0;
      if(i%prime[j]==0){
        phi[i*prime[j]]=phi[i]*prime[j];
        break;
      }
      else phi[i*prime[j]]=phi[i]*(prime[j]-1);
    }
  }
  return cnt;
}
struct poly{
  int x,y;
  poly operator+(poly a){
    return (poly){(x+a.x)%mod,(y+a.y)%mod};
  }
  poly operator-(poly a){
    return (poly){(x-a.x+mod)%mod,(y-a.y+mod)%mod};
  }
  poly operator*(poly a){
    return (poly){(1ll*x*a.y%mod+1ll*y*a.x%mod)%mod,1ll*y*a.y%mod};
  }
  poly getinv(){
    if(!y)return (poly){inv(x,mod),0};
    int temp=inv(y,mod);
    return (poly){1ll*(mod-x)*temp%mod*temp%mod,temp};
  }
}a[35][35];
template<int maxn>poly det(int n,poly a[maxn][maxn],poly ans=(poly){0,1}){
  for(int i=1;i<=n;i++){
    int pos=i;
    for(int j=i;j<=n;j++)if((!a[i][i].y&&a[j][i].y)||(!a[i][i].x&&!a[i][i].y&&a[j][i].x))pos=j;
    if(i!=pos)swap(a[i],a[pos]),ans=(poly){0,0}-ans;
    poly temp=a[i][i].getinv();
    for(int j=i+1;j<=n;j++)for(int k=n;k>=i;k--)a[j][k]=a[j][k]-a[i][k]*a[j][i]*temp;
  }
  for(int i=1;i<=n;i++)ans=ans*a[i][i];
  return ans;
}
int solve(int d){
  memset(a,0,sizeof(a));
  int cnt=0;
  for(int i=1;i<=m;i++){
    if(e[i].w%d)continue;
    cnt++;
    a[e[i].u][e[i].u]=a[e[i].u][e[i].u]+(poly){e[i].w,1};
    a[e[i].v][e[i].v]=a[e[i].v][e[i].v]+(poly){e[i].w,1};
    a[e[i].u][e[i].v]=a[e[i].u][e[i].v]-(poly){e[i].w,1};
    a[e[i].v][e[i].u]=a[e[i].v][e[i].u]-(poly){e[i].w,1};
  }
  return cnt>=n-1?det(n-1,a).x:0;
}
int main(){
  cin>>n>>m;
  for(int i=1;i<=m;i++)cin>>e[i].u>>e[i].v>>e[i].w,maxn=max(maxn,e[i].w);
  phi_init(maxn,prime,phi,vis);
  for(int i=1;i<=maxn;i++)ans=(ans+1ll*phi[i]*solve(i)%mod)%mod;
  return cout<<ans<<'\n',0;
}

UOJ75

考虑随机化。随机一个比较稠密的图，每条边出现的概率为 $0.8$。当 $n=15$ 时，图的生成树个数已经远大于 $998244353$，因此可以看作一个随机数。

将两张图连一条边，新图的生成树个数为两张图的乘积。因此，我们只需要随机大概 $1000$ 张，每四张图合并，就能得到 $10^{12}$ 个随机数，$k$ 在里面出现的概率几乎为 $1$。

找这四张图，可以先预处理每两张图合并的生成树个数扔进 map，对每个询问再枚举剩下两张。

$0$ 比较特别，必须有 $0$ 才能组合出 $0$，概率远小于其他的数，需要特判。

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
int t,k,temp[20][20],dis[1005][20][20],m[1005],v[1005];
map<int,pair<int,int>>p;
template<typename T>T qpow(T a,T b,T n,T ans=1){
  for(a%=n;b;b>>=1)b&1&&(ans=1ll*ans*a%n),a=1ll*a*a%n;
  return ans;
}
template<typename T>T inv(T a,T b)
{
  return qpow(a,b-2,b);
}
template<int maxn>int det(int n,int a[maxn][maxn],int ans=1){
  for(int i=1;i<=n;i++){
    for(int j=i+1,t;j<=n;j++){
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++)a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)ans=1ll*ans*a[i][i]%mod;
  return (ans+mod)%mod;
}
void out(int a,int b,int c,int d){
  cout<<"60 "<<m[a]+m[b]+m[c]+m[d]+3<<"\n1 16\n16 31\n31 46\n";
  for(int i=1;i<=15;i++)for(int j=i+1;j<=15;j++)if(dis[a][i][j])cout<<i<<' '<<j<<'\n';
  for(int i=1;i<=15;i++)for(int j=i+1;j<=15;j++)if(dis[b][i][j])cout<<i+15<<' '<<j+15<<'\n';
  for(int i=1;i<=15;i++)for(int j=i+1;j<=15;j++)if(dis[c][i][j])cout<<i+30<<' '<<j+30<<'\n';
  for(int i=1;i<=15;i++)for(int j=i+1;j<=15;j++)if(dis[d][i][j])cout<<i+45<<' '<<j+45<<'\n';
}
int main(){
  srand(time(NULL));
  for(int i=1;i<=1000;i++){
    memset(temp,0,sizeof(temp));
    for(int j=1;j<=15;j++){
      for(int k=j+1;k<=15;k++){
        if(rand()%10<=7)temp[j][j]++,temp[k][k]++,temp[j][k]--,temp[k][j]--,dis[i][j][k]++,dis[i][k][j]++,m[i]++;
      }
    }
    v[i]=det(14,temp);
  }
  for(int i=1;i<=1000;i++)for(int j=i;j<=1000;j++)p[1ll*v[i]*v[j]%mod]=make_pair(i,j);
  cin>>t;
  while(t--){
    cin>>k;
    if(!k){
      puts("2 0");
      continue;
    }
    for(int i=1;i<=1000;i++){
      for(int j=i;j<=1000;j++){
        int temp=1ll*k*inv(1ll*v[i]*v[j]%mod,(long long)mod)%mod;
        if(p.count(temp)){
          out(i,j,p[temp].first,p[temp].second);
          goto tag;
        }
      }
    }
    tag:;
  }
  return 0;
}

BEST 定理

BSET 定理可以数有向图的欧拉回路。对于有向欧拉图 $G$，从点 $s$ 开始的欧拉回路的数量为：

\[out_s!t^{root}(G,s)\prod_{1\leq i\leq n,i\ne s}(out_i-1)! \]

证明：

对于一条欧拉回路，取出除了点 $s$ 之外所有点的最后一条出边，一定形成以 $s$ 为根的根向树形图。如果有环，走完这个环上的最后一条边会停留在环上某个点，而这个点已经用完了所有出边，矛盾。

如果已经确定了这个树形图，对于每个点的剩下的出边任意排列，都可以形成欧拉回路。因此答案为 $out_s!t^{root}(G,s)\prod_{1\leq i\leq n,i\ne s}(out_i-1)!$。

假如不给定起点，数量为 $t^{root}(G,s)\prod_{i=1}^n(out_i-1)!$。这个式子去掉了循环同构的欧拉回路，也就是一个回路从任意一个位置断开算一条。如果给定起点，这个起点在回路中出现了 $out_s$ 次，就重复算了 $out_s$ 次，除掉就得到这个式子。

欧拉回路数量和 $s$ 没有关系，所以有向欧拉图以任意节点为根的树形图数量相同。而且出度等于入度，所以上面的式子用叶向树形图和入度也一样。

P5807

模版题。细节较多，要去掉孤立点，并且考虑 $1$ 为孤立点的情况。

#include<bits/stdc++.h>
using namespace std;
const int mod=1000003;
int t,n,fac[200005],in[105],out[105],f[105],a[105][105],ans;
vector<int>e[105];
int find(int x){
  return f[x]?f[x]=find(f[x]):x;
}
bool merge(int x,int y){
  int f1=find(x),f2=find(y);
  return f1==f2?0:(f[f1]=f2,1);
}
template<int maxn>int det(int n,int a[maxn][maxn],int ans=1){
  for(int i=1;i<=n;i++){
    if(i==1||!out[i])continue;
    for(int j=i+1,t;j<=n;j++){
      if(!out[j])continue;
      while(a[i][i]){
        t=a[j][i]/a[i][i];
        for(int k=i;k<=n;k++){
          if(k==1||!out[k])continue;
          a[j][k]=(a[j][k]-1ll*t*a[i][k]%mod+mod)%mod;
        }
        swap(a[i],a[j]),ans=-ans;
      }
      swap(a[i],a[j]),ans=-ans;
    }
  }
  for(int i=1;i<=n;i++)if(i!=1&&out[i])ans=1ll*ans*a[i][i]%mod;
  return (ans+mod)%mod;
}
int main(){
  fac[0]=1;
  for(int i=1;i<=200000;i++)fac[i]=1ll*fac[i-1]*i%mod;
  cin>>t;
  while(t--){
    cin>>n;
    for(int i=1,s;i<=n;i++){
      cin>>s;
      for(int j=1,x;j<=s;j++)cin>>x,e[i].push_back(x),a[i][i]++,a[i][x]--,in[x]++,out[i]++,merge(i,x);
    }
    for(int i=1;i<=n;i++){
      if(in[i]!=out[i]||(find(i)!=find(1)&&out[i])){
        puts("0");
        goto tag;
      }
    }
    ans=det(n,a);
    for(int i=1;i<=n;i++)if(out[i])ans=1ll*ans*(i==1?fac[out[i]]:fac[out[i]-1])%mod;
    cout<<ans<<'\n';
    tag:memset(in,0,sizeof(in)),memset(out,0,sizeof(out)),memset(f,0,sizeof(f)),memset(a,0,sizeof(a));
    for(int i=1;i<=n;i++)e[i].clear();
  }
  return 0;
}

AT_agc051_d

先给边定向，设 $1\to 2,2\to 3,3\to 4,4\to 1$ 分别有 $e,f,g,h$ 次。枚举 $e$，因为定向之后每个点的出度等于入度，所以 $a-e+f=e+b-f,f=\frac{b-a+2e}2$。同理可以知道 $f,g,h$。如果相邻两条边的经过次数的奇偶性不同则无解。

然后算每个点的度数，设为 $u,v,w,x$ 套用 BEST 定理可以知道答案为 $[uvw-uf(b-f)-e(a-e)w]u!(v-1)!(w-1)!(x-1)!$。这题要求每条边不区分，要除以 $e!f!g!h!(a-e)!(b-f)!(c-g)!(d-h)!$。

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
int a,b,c,d,fac[1000005],vac[1000005],ans;
int main(){
  fac[0]=vac[0]=vac[1]=1,cin>>a>>b>>c>>d;
  if(a&1^b&1||b&1^c&1||c&1^d&1||d&1^a&1)return puts("0"),0;
  for(int i=2;i<=1000000;i++)vac[i]=1ll*(mod-mod/i)*vac[mod%i]%mod; 
  for(int i=1;i<=1000000;i++)fac[i]=1ll*fac[i-1]*i%mod,vac[i]=1ll*vac[i]*vac[i-1]%mod; 
  for(int e=0;e<=a;e++){
    int f=(b-a+2*e)/2,g=(c-b+2*f)/2,h=(d-c+2*g)/2,u=e+d-h,v=f+a-e,w=g+b-f,x=h+c-g;
    if(f<0||f>b||g<0||g>c||h<0||h>d)continue;
    ans=(ans+1ll*((1ll*u*v*w-1ll*u*f*(b-f)-1ll*e*(a-e)*w)%mod+mod)%mod*fac[u]%mod*fac[v-1]%mod*fac[w-1]%mod*fac[x-1]%mod*vac[e]%mod*vac[f]%mod*vac[g]%mod*vac[h]%mod*vac[a-e]%mod*vac[b-f]%mod*vac[c-g]%mod*vac[d-h]%mod)%mod;
  }
  return cout<<ans<<'\n',0;
}

[[数学]]

posted @ 2024-03-01 09:35 lgh_2009 阅读(110) 评论(0) 收藏举报

刷新页面返回顶部

lgh-blog

qwq