高中数学必修一摘要

1 集合与常用逻辑用语

集合的定义：把研究对象统称为元素，把一些元素组成的总体叫做集合。元素可以是任何东西，比如数字、字符、线段甚至集合本身等。集合就是一堆元素。

集合具有确定性、互异性、无序性。集合中的元素必须确定，元素互不相同，并且没有顺序之分。

若构成两个集合的元素一样，则这两个集合相等。

若 \(a\) 是集合 \(A\) 的元素，则 \(a\) 属于 \(A\)，记作 \(a\in A\)。否则 \(a\) 不属于 \(A\)，记作 \(a\notin A\)。

一些常用的数集：自然数集 \(\mathbb{N}\)，整数集 \(\mathbb{Z}\)，有理数集 \(\mathbb{Q}\)，实数集 \(\mathbb{R}\)。另外，星号上标和加号下标表示正数，负号下标表示负数。比如正整数集 \(\mathbb{N}^\ast,\mathbb{N}_+\)，负整数集 \(\mathbb{Z}_-\)。

集合的表示方法：列举法、描述法。

列举法是把集合中的全部元素列出来，如 \(A=\{1,2,3\}\)。

取出一个集合 \(A\) 中有共同特征 \(P(x)\) 的元素组成一个新的集合，记作 \(\{x\in A\mid P(x)\}\)。这是描述法。

集合间的基本关系：

如果集合 \(A\) 的所有元素属于 \(B\)，则称 \(A\) 是 \(B\) 的子集，记作 \(A\subseteq B\)。如果 \(A\) 是 \(B\) 的子集但不等于 \(B\)，那么 \(A\) 是 \(B\) 的真子集，记作 \(A\subsetneqq B\)。

如果 \(A\) 是 \(B\) 的子集，那么 \(B\) 包含 \(A\)，记作 \(B\supseteq A\)。同样可以定义真包含 \(\supsetneqq\)。显然属于和包含具有自反性和传递性。

不含任何元素的集合记作 \(\varnothing\)。它是任何集合的子集。

集合的基本运算：

先规定三种逻辑运算 \(\wedge,\vee,\neg\)，分别表示与或非。

集合 \(A,B\) 的并集 \(A\cup B=\{x\mid x\in A\vee x\in B\}\) 表示并集的元素属于 \(A\) 或属于 \(B\)；

集合 \(A,B\) 的交集 \(A\cap B=\{x\mid x\in A\wedge x\in B\}\) 表示并集的元素属于 \(A\) 且属于 \(B\)；

如果一个集合包含所研究问题中涉及的全部元素，那么这个集合为全集 \(U\)。全集的定义会视情况改变。

集合 \(A\) 相对于全集 \(U\) 的补集 \(\complement_U A=\{x\mid x\in U\wedge x\notin A\}\)，表示全集去掉 \(A\) 的剩余。

补充一下，差集 \(A-B=\{x\mid x\in A\wedge x\notin B\}\)，对称差集 \(A\Delta B=(A-B)\cup(B-A)\)。

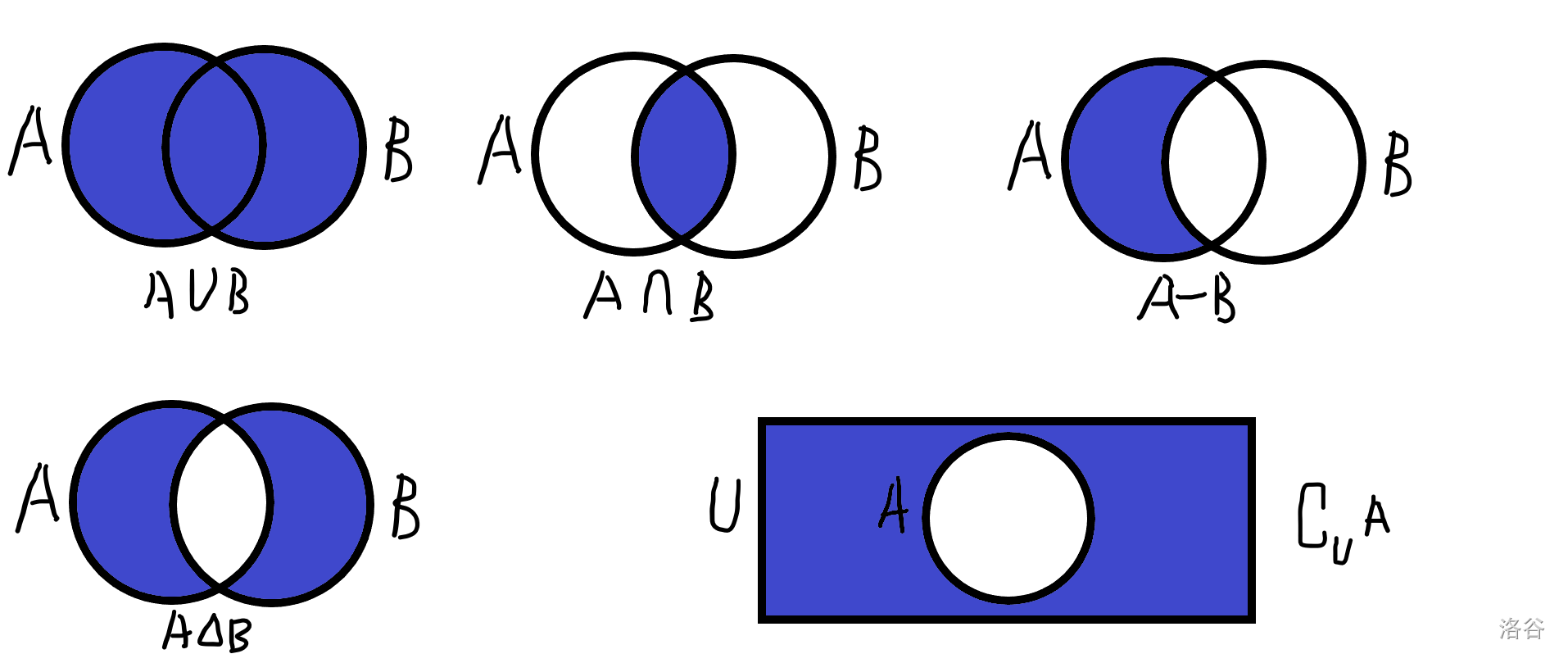
如果用 bitset 表示集合，那么可用按位与、按位或、按位异或表示集合的并、交、对称差。

定义集合 \(A\) 中元素的个数为 \(\operatorname{card}(A)\)。求解一些集合交、并的元素个数的问题可以使用容斥原理。

充分条件和必要条件：

两个命题 \(p,q\)，若 \(p\) 能推出 \(q\)，记作 \(p\Rightarrow q\)，则称 \(p\) 是 \(q\) 的充分条件，即有 \(p\) 就有 \(q\)；\(q\) 是 \(p\) 的必要条件，有 \(p\) 必须要先有 \(q\)。如果推不出，记作 \(p\nRightarrow q\)。

如果 \(p,q\) 能互推，\(p\Leftrightarrow q\)，那么 \(p,q\) 互为充要条件。

全称量词与存在量词：

符号 \(\forall\) 为全称量词，表示任意一个。比如全称量词命题 \(\forall x\in M,p(x)\) 意为对于任意的 \(x\in M\) 都有 \(p(x)\) 成立。

符号 \(\exists\) 为存在量词，表示存在一个。比如存在量词命题 \(\exist x\in M,p(x)\) 意为存在一个 \(x\in M\) 使 \(p(x)\) 成立。

全称量词命题的否定形式为 \(\exists x\in M,\neg p(x)\)。存在量词命题的否定形式为 \(\forall x\in M,\neg p(x)\)。

2 一元二次函数、方程和不等式

根据初一知识，不等式有一些显然的性质：

\[\begin{aligned}a>b\Leftrightarrow a-b>0\\a=b\Leftrightarrow a-b=0\\a<b\Leftrightarrow a-b<0\\a>b\Leftrightarrow b<a\\a>b,b>c\Rightarrow a>c\\a>b\Rightarrow a+c>b+c\\a>b,c>0\Rightarrow ac>bc\\a>b,c>0\Rightarrow ac<bc\\a>b,c>d\Rightarrow a+b>c+d\\a>b>0,c>d>0\Rightarrow ab>cd\\a>b>0\Rightarrow a^n>b^n(n\in\mathbb{N},n\geq2)\end{aligned} \]

基本不等式是一个重要的不等式。

\[\begin{aligned}(\sqrt a-\sqrt b)\geq 0\\a+b-2\sqrt{ab}\geq 0\\\sqrt{ab}\leq\frac{a+b}{2} \end{aligned} \]

当且仅当 \(a=b\) 时取到等号。通过它可以解决许多问题。

一元二次不等式是形如 \(ax^2+bx+c>0\) 或 \(ax^2+bx+c<0\) 的不等式。其中 \(a,b,c\) 为常数，\(a\ne 0\)。解这类不等式可以讨论不等号左边的零点。

3 函数的概念与性质

函数的定义：

两个非空集合 \(A,B\) 存在一个对应关系，使 \(A\) 的每一个元素 \(x\) 在 \(B\) 中都有唯一的一个元素 \(y\) 对应，那么称这个对应关系是 \(A\) 到 \(B\) 的一个映射，记作 \(f:A\to B\)。

而函数是一个非空数集到另一个非空数集的映射，记为 \(y=f(x),x\in A\)。其中 \(x\) 为自变量，\(A\) 为定义域，\(y\) 为函数值，\(y\) 的集合 \(\{f(x)\mid x\in A\}\) 为值域。

区间：

区间的两个端点为 \(a,b(a<b)\)。那么 \(a\) 到 \(b\) 之间的所有数组成的集合为区间。分为闭区间 \([a,b]\)、开区间 \((a,b)\)、左闭右开区间 \([a,b)\)、左开右闭区间 \((a,b]\)。闭表示端点能取到，开表示端点不能取到。

单调性：

记函数的定义域为 \(I\)。如果函数 \(f(x)\) 在区间 \(D\) 上一直上升，形式化语言为 \(\forall x_1,x_2\in D\wedge x_1<x_2,f(x_1)<f(x_2)\)，称函数 \(f(x)\) 在区间 \(D\) 上单调递增。如果函数在定义域上单调递增，称这个函数为增函数。

类似可以定义单调递减和减函数。

奇偶性：

如果函数关于 \(y\) 轴对称，即 \(\forall x\in I,-x\in I\wedge f(-x)=f(x)\)，这个函数为偶函数。

如果函数关于原点中心对称，即 \(\forall x\in I,-x\in I\wedge f(-x)=-f(x)\)，这个函数为奇函数。

幂函数：

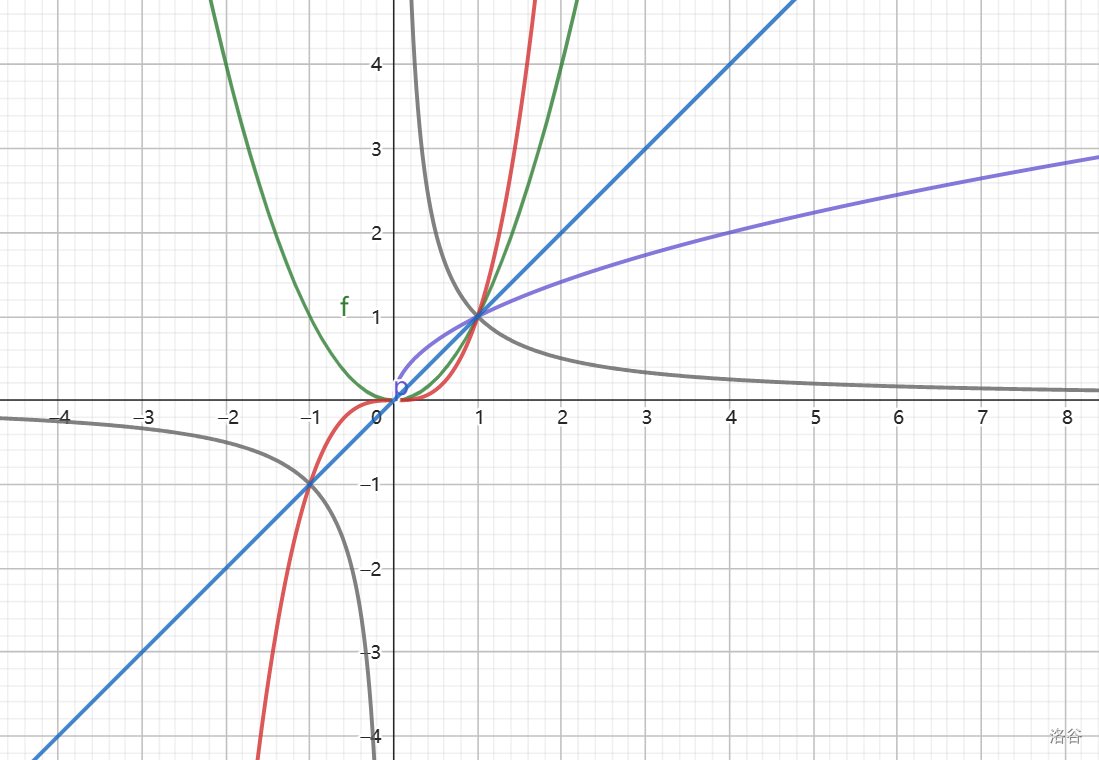
形如 \(y=x^\alpha\) 的函数叫幂函数。探究 \(\alpha=1,2,3,\frac 1 2,-1\) 的性质：

由 \(1^\alpha=1\) 可知这些函数过 \((1,1)\)。

\(\alpha=1,3,-1\) 时是奇函数，\(\alpha=2\) 时是偶函数。

在 \((0,+\infty)\) 上，只有 \(\alpha=-1\) 时单调递减，其他单调递增。

对勾函数与飘带函数：

书上只讲了 \(y=x+\frac 1 x\)，不过可以扩展至 \(y=ax+\frac b x(ab>0)\) 和 \(y=ax-\frac b x(ab>0)\)。

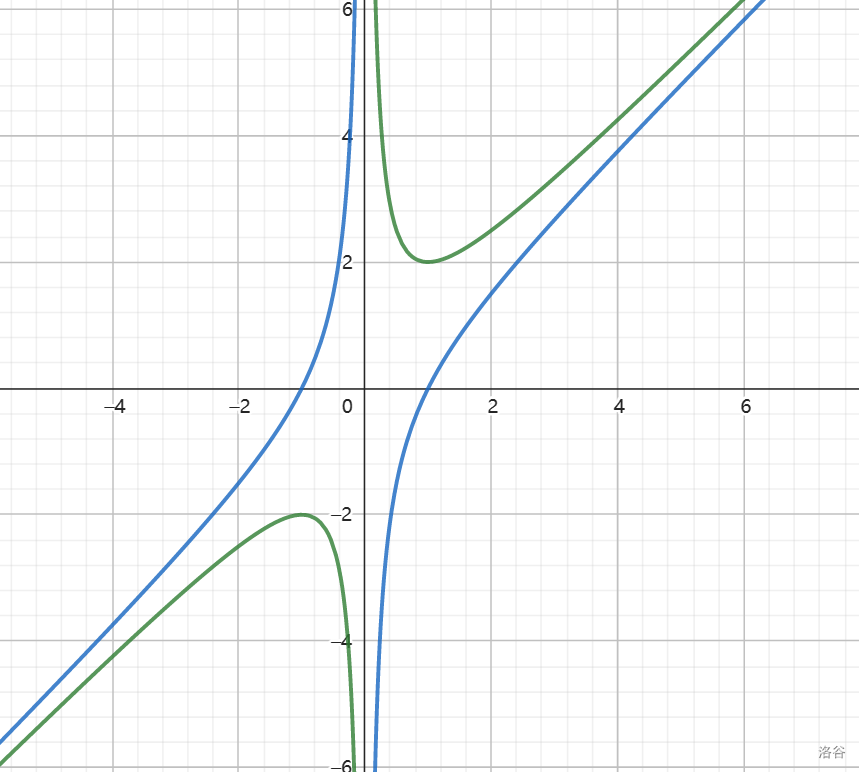
\(y=ax+\frac b x(ab>0)\) 是对勾函数，为奇函数。图像在第一象限上先减后增，在第四象限上先增后减，形成对勾。通过基本不等式可得拐点 \((\pm\sqrt\frac b a,\pm2\sqrt{ab})\)。

\(y=ax-\frac b x(ab>0)\) 是飘带函数，为奇函数。图像的两部分都是单调递增。有两个零点 \((\pm\sqrt\frac b a,0)\)。

4 指数函数与对数函数

指数：

根据初二知识，可以仿照平方根定义 \(n\) 次方根，当 \(x^n=a(n>1,n\in \mathbb{N}^\ast)\)，称 \(x\) 是 \(a\) 的 \(n\) 次方根。正的 \(n\) 次方根用根式 \(\sqrt[n]{a}\) 表示。\(n\) 是根指数，\(a\) 是被开方数。

\((\sqrt[n]{a^m})^n=a^m,\sqrt[n]{a^m}=a^{\frac{m}{n}}(a>0,m,n\in \mathbb{N}^\ast,n>1)\)。这样就定义了正数的正分数指数幂。正数的负分数指数幂是正分数指数幂的倒数。\(0\) 的正分数指数幂等于 \(0\)，负分数指数幂无意义。

形如 \(y=a^x(a>0\wedge a\ne1)\) 的函数为指数函数。

按照 \(a\) 分为两种，当 \(0<a<1\) 时是减函数，\(a>1\) 时是增函数。任何非零数的 \(0\) 次幂等于一，因此恒过 \((0,1)\)。定义域 \(\mathbb{R}\)，值域 \((0,+\infty)\)。

对数：

如果 \(a^x=N(a>0\wedge a\ne1)\)，那么 \(x\) 是以 \(a\) 为底 \(N\) 的对数,记作 \(x=\log_a N\)。\(a\) 为底数，\(N\) 为真数。负数和 \(0\) 没有对数。

对数常用两个底数 \(10\) 和 \(e\)。其中 \(e\) 是自然对数，约等于 \(2.71828\cdots\)。这个东西很神奇，是一个重要的无理数。记 \(\log_{10}\) 为 \(\lg\)，\(\log_e\) 为 \(\ln\)。

通过幂的性质可以推得对数的性质。设 \(M=a^m,N=a^n\)：

\(\log_a{(MN)}=\log_a{a^{m+n}}=m+n=\log_a M+\log_a N\)；

\(\log_a{\frac M N }=\log_a{a^{m-n}}=m-n=\log_a M-\log_a N\)；

\(\log_a{M^N}=N\log_a M\)。

设 \(a^x=b\)，\(\log_c a^x=x\log_c a=\log_c b\)，\(\log_a b=\frac{\log_c b}{\log_c a}(a>0\wedge a\ne1,b>0,c>0\wedge c\ne1)\)。

上面的式子是对数换底公式，这样只需要求一个底数的对数就可以算所有底数的对数。因此 C++ 中只有 \(10,2,e\) 的常用对数。

形如 \(y=\log_a x(a>0\wedge a\ne 1)\) 的函为对数函数。

对数函数与指数函数有很多关联。对数函数的图像就像指数函数右旋 \(90\degree\)，恒过 \((1,0)\)。当 \(0<a<1\) 时是减函数，\(a>1\) 时是增函数。

对数函数与指数函数的值域与定义域相反，并且 \(\log_a a^x=x\)。如果两个函数 \(f(x),g(x)\) 值域与定义域互换，对于 \(f(x)\) 值域中的每一个 \(y\) 在定义域中都有且仅有一个 \(x\) 使 \(g(y)=x\)，那么 \(f(x),g(x)\) 互为反函数。对数函数和指数函数互为反函数。

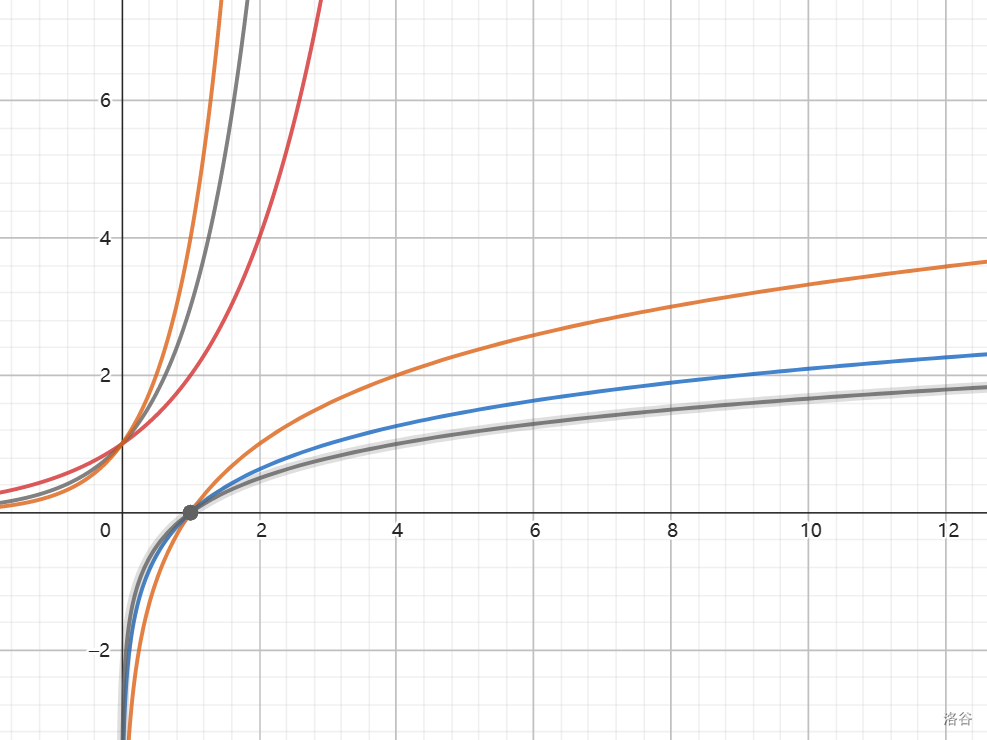
使 \(f(x)=0\) 的实数 \(x\) 叫做函数 \(y=f(x)\) 的零点。

函数零点存在定理：如果函数 \(y=f(x)\) 在 \([a,b]\) 上连续，且 \(f(a)f(b)<0\)，则函数 \(y=f(x)\) 在区间 \((a,b)\) 内至少有一个零点。感性理解一下，\(f(a)f(b)<0\)，\(y=f(x)\) 在 \([a,b]\) 上连续，那么从 \(a\) 走到 \(b\) 必然穿过 \(x\) 轴。

书上居然有二分法，我的评价是6

5 三角函数

根据小学知识，具有公共端点的两条射线叫做角。但是这样只能定义 \(0\degree\sim 360\degree\) 的角，需要扩大角的范围。

定义一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角。逆时针旋转为正角，顺时针为负角。没有旋转则为零角。这就定义了任意角。

在平面直角坐标系上，假设角的顶点与原点重合，始边在 \(x\) 轴上，终边在第几个象限，称这个角为第几象限角。

介绍角的一种新单位：弧度制。长度等于半径长的圆弧所对的圆心角为一弧度角，记作 \(1 \operatorname{rad}\)。弧度制可以把角和长度的计算统一，因此有些时候不会加上单位，把角度看作一个值。\(360\degree=2\pi\operatorname{rad}\)。

三角函数的定义：

初中通过直角三角形定义了锐角三角函数，但现在需要一个新的方式定义三角函数，使得定义域来到全体实数。

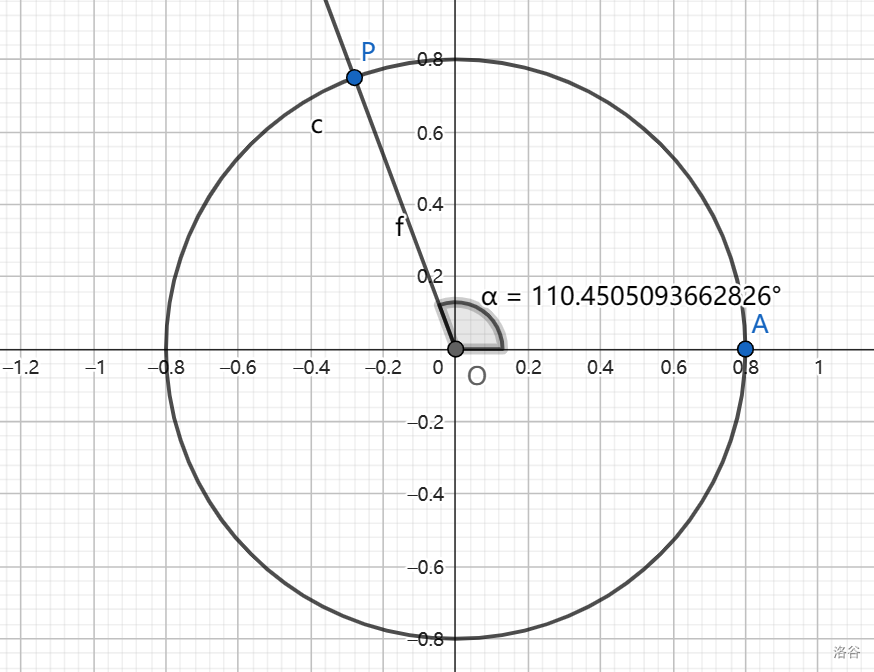
设 \(\alpha\) 是一个任意角，终边 \(OP\) 交单位圆于 \(P(x,y)\)，则 \(\sin\alpha=x,\cos\alpha=y,\tan\alpha=\frac{x}{y}\)，分别叫正弦函数、余弦函数、正切函数，统称三角函数。

当 \(OP\) 在 \(y\) 轴上，\(\tan\) 的分母为零，无意义。因此正切要求 \(\alpha\ne\frac\pi 2+k\pi(k\in\mathbb{Z})\)。

显然终边相同的角三角函数也相同，因此有：

\[\sin(\alpha+k\cdot2\pi)=\sin\alpha,\cos(\alpha+k\cdot2\pi)=\cos\alpha,\tan(\alpha+k\cdot2\pi)=\tan\alpha(k\in\mathbb{Z}) \]

根据定义，\(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\)。

根据勾股定理，\(\sin^2\alpha+\cos^2\alpha=OP^2=1\)。

诱导公式：

根据单位圆的对称性可以得到诱导公式。

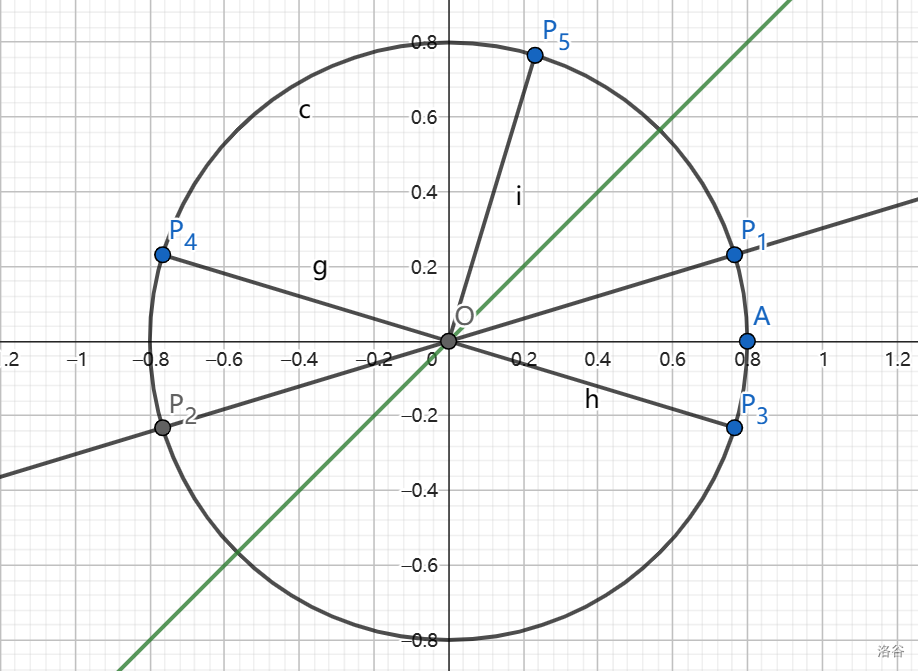
作 \(P_1\) 关于原点的对称点 \(P_2\)，可得 \(\sin(\pi+\alpha)=-\sin\alpha,\cos(\pi+\alpha)=-\cos\alpha,\tan(\pi+\alpha)=\tan\alpha\)

作 \(P_1\) 关于 \(x\) 轴的对称点 \(P_3\)，可得 \(\sin(-\alpha)=-\sin\alpha,\cos(-\alpha)=\cos\alpha,\tan(-\alpha)=-\tan\alpha\)

作 \(P_1\) 关于 \(y\) 轴的对称点 \(P_4\)，可得 \(\sin(\pi-\alpha)=\sin\alpha,\cos(\pi-\alpha)=-\cos\alpha,\tan(\pi-\alpha)=-\tan\alpha\)

作 \(P_1\) 关于直线 \(y=x\) 的对称点 \(P_5\)，可得 \(\sin(\frac\pi2-\alpha)=\cos\alpha,\cos(\frac\pi2-\alpha)=\sin\alpha\)

对 \(P_5\) 用 \(P_4\) 的结论可得 \(\sin(\frac\pi2+\alpha)=\cos\alpha,\cos(\frac\pi2+\alpha)=-\sin\alpha\)

正弦函数、余弦函数的图像和性质：

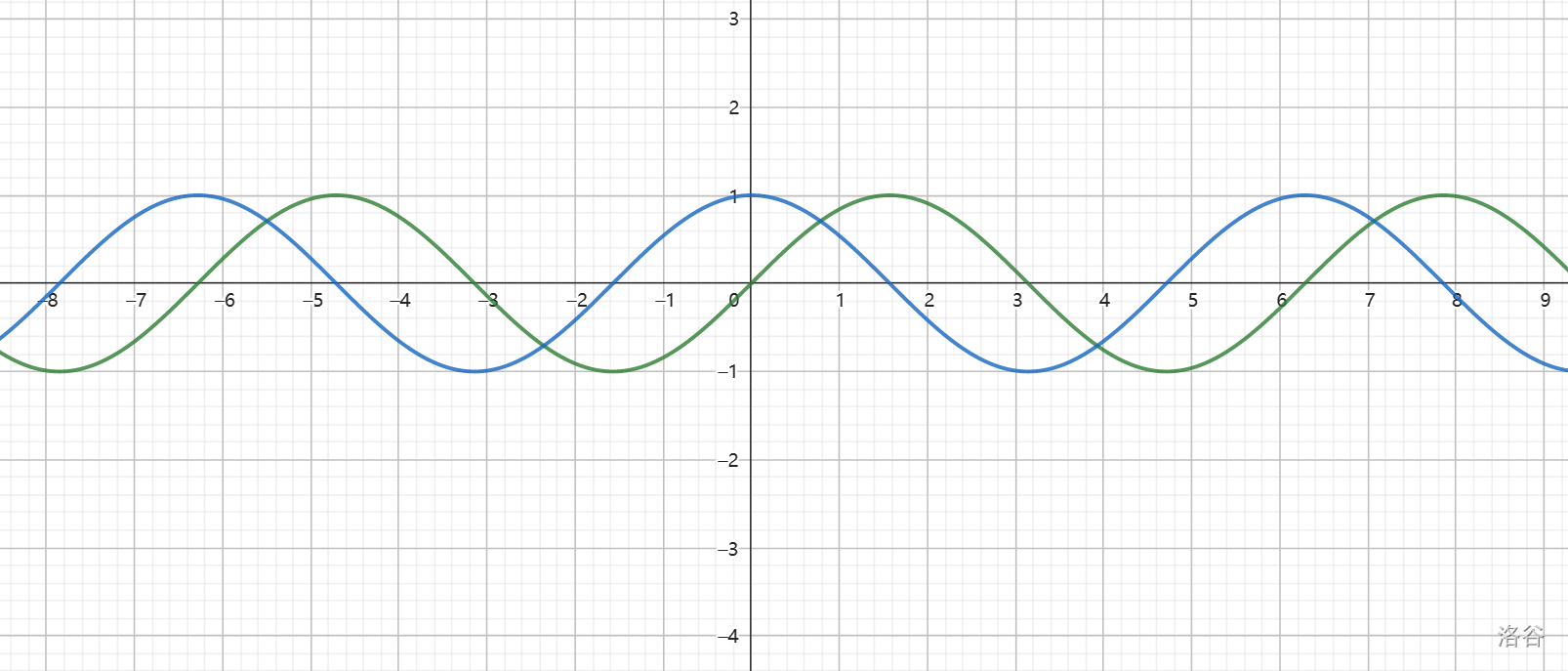
如图，绿色为正弦曲线，蓝色为余弦曲线。

余弦曲线是正弦曲线向左平移 \(\frac\pi2\) 得到，因为 \(\sin(\frac\pi2-\alpha)=\cos\alpha\)。

由 \(\sin(-\alpha)=-\sin\alpha,\cos(-\alpha)=\cos\alpha\) 得正弦函数是奇函数，余弦函数是偶函数。

正弦函数和余弦函数每隔 \(2\pi\) 就重复一次，这种性质为周期性。若函数 \(f(x)\) 的定义域为 \(D\)，存在一个非零常数 \(T\) 使 \(\forall x\in D,x+T\in D\wedge f(x+T)=f(x)\)，则 \(f(x)\) 是周期函数，\(T\) 是这个函数的周期。一般周期默认为最小正周期。正弦函数和余弦函数的周期为 \(2\pi\)。

由图像得，正弦函数在 \([-\frac\pi2+2k\pi,\frac\pi2+2k\pi](k\in\mathbb Z)\) 单调递增，在 \([\frac\pi2+2k\pi,\frac{3\pi}2+2k\pi](k\in\mathbb Z)\) 单调递减。余弦函数则分别是 \([-\pi+2k\pi,2k\pi],[2k\pi,\pi+2k\pi](k\in\mathbb Z)\)。

正弦函数在 \(\frac\pi2+2k\pi(k\in\mathbb Z)\) 处取到最大值 \(1\)，在 \(-\frac\pi2+2k\pi(k\in\mathbb Z)\) 处取到最小值 \(-1\)；余弦函数在 \(2k\pi(k\in\mathbb Z)\) 处取到最大值 \(1\)，在 \(-\pi+2k\pi(k\in\mathbb Z)\) 处取到最小值 \(-1\)。

给正弦函数和余弦函数加几个参数，变为 \(y=A\sin(\omega x+\varphi)+B\) 和 \(y=A\cos(\omega x+\varphi)+B\)。

其中，\(\omega,\varphi\) 在括号内，影响 \(x\)。\(\omega\) 乘在 \(x\) 上，会使图像横向放缩，周期变为 \(\frac{2\pi}{\omega}\)；\(\varphi\) 则是左右平移。同理，\(A,B\) 分别会让函数纵向放缩与平移。

正切函数的图像和性质：

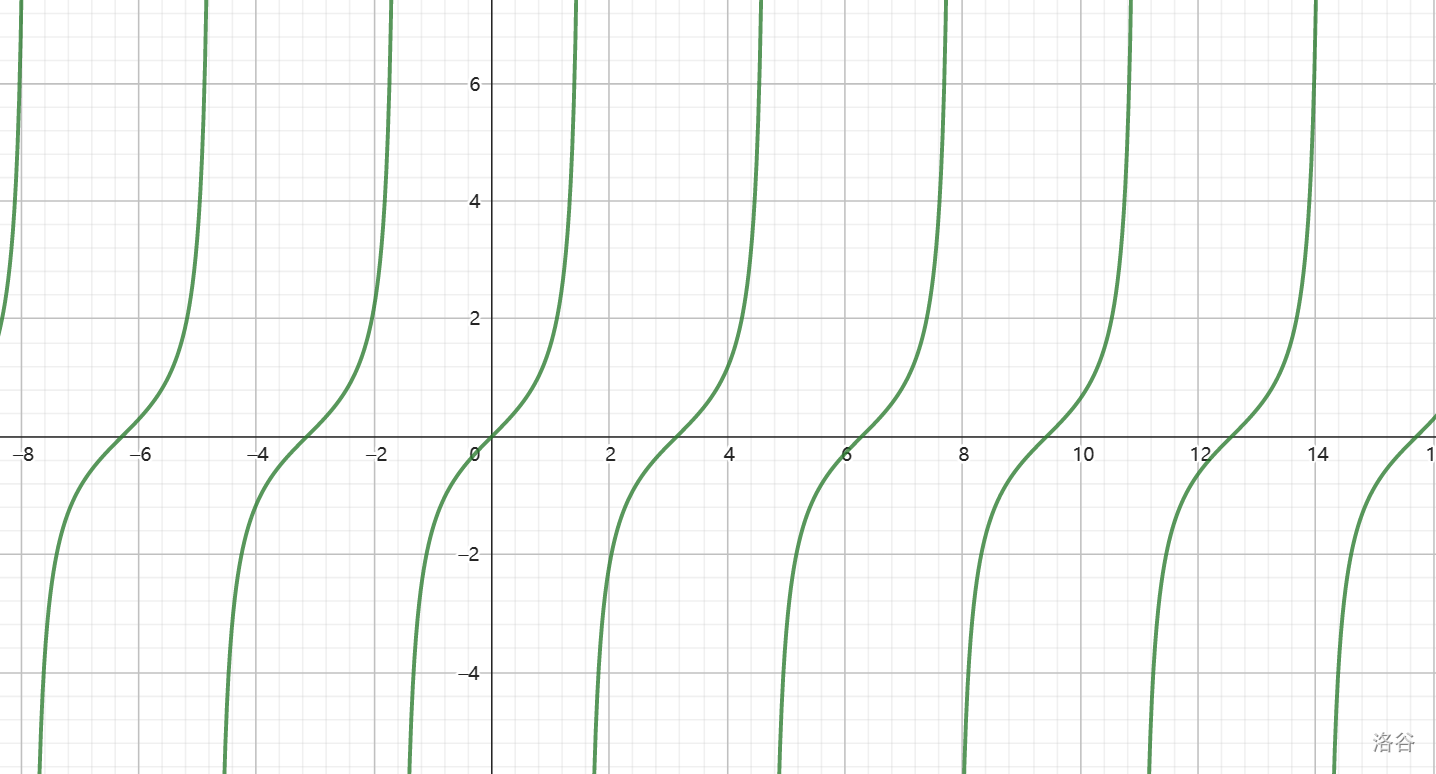
由 \(\tan(\pi+\alpha)=\tan\alpha\) 得正切函数的周期是 \(\pi\)。由 \(\tan(-\alpha)=-\tan\alpha\) 得正切函数是奇函数。

由图像得，正切函数在 \((-\frac\pi2+k\pi,\frac\pi2+k\pi)(k\in\mathbb Z)\) 上单调递增。每一条曲线都向上向下无限延伸，值域为 \(\mathbb R\)。

三角恒等变换：

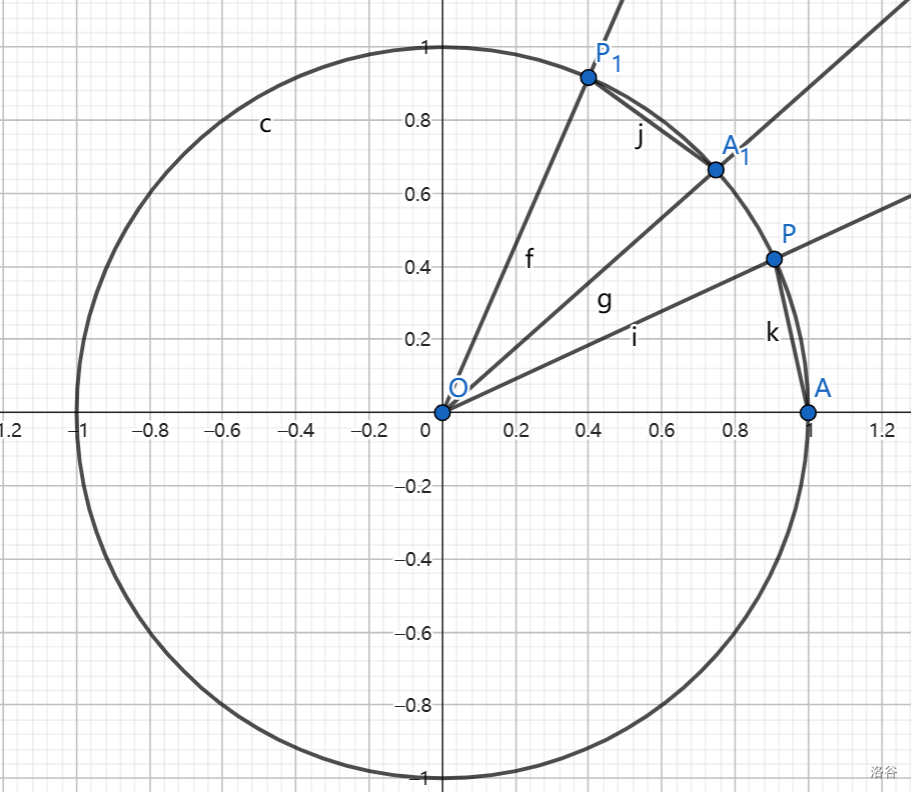
\(\angle AOP_1=\alpha,\angle AOA_1=\beta\)。作 \(\angle AOP=\alpha-\beta\)，显然 \(\triangle AOP\cong\triangle A_1OP_1\)，\(AP=A_1P_1\)。

\[\begin{aligned}(X_P-X_A)^2+(Y_P-Y_P)^2&=(X_{P_1}-X_{A_1})^2+(Y_{P_1}-Y_{A_1})^2\\ [\cos(\alpha-\beta)-1]^2+\sin^2(\alpha-\beta)&=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)\\\cos^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+\sin^2(\alpha-\beta)&=\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta\\2-2\cos(\alpha-\beta)&=2-2\cos\alpha\cos\beta-2\sin\alpha\sin\beta\\\cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\end{aligned} \]

\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\) 是差角的余弦公式，记作 \(C_{\alpha-\beta}\)。

把减一个数换成加一个数的相反数，可得 \(C_{\alpha+\beta}\) \(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)。

通过诱导公式可以互化 \(\sin,\cos\)，得到 \(S_{\alpha-\beta}\)：

\[\begin{aligned}\sin(\alpha-\beta)&=\cos{(\frac\pi2-\alpha+\beta)}\\&=\cos(\frac\pi2-\alpha)\cos\beta-\sin(\frac\pi2-\alpha)\sin\beta\\&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\end{aligned} \]

类似可得 \(S_{\alpha+\beta}\)：\(\sin(\alpha+\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)。

通过 \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\) 可得差角的正切公式 \(T_{\alpha-\beta}\)：

\[\begin{aligned}\tan(\alpha-\beta)&=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\&=\frac{\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta-\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\&=\frac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta}}{1-\frac{\sin\alpha\cos\alpha}{\sin\beta\cos\beta}}\\&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\end{aligned} \]

类似可得 \(T_{\alpha+\beta}\)：\(\tan(\alpha+\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\)。

当 \(\alpha=\beta\)，可以得到和角公式的特殊情况：二倍角公式 \(S_{2\alpha},C_{2\alpha},T_{2\alpha}\)。

\[\begin{aligned}\sin2\alpha&=2\sin\alpha\cos\alpha\\\cos2\alpha&=\cos^2\alpha-\sin^2\alpha=1-2\sin^2\alpha=2\cos^2\alpha-1\\\tan2\alpha&=\frac{2\tan\alpha}{1-\tan^2\alpha}\end{aligned} \]

对 \(S_{2\alpha}\) 变形可得 \(1\pm\sin2\alpha=\sin^2\alpha+\cos^2\alpha\pm2\sin\alpha\cos\alpha=(\sin\alpha\pm\cos\alpha)^2\)。

对 \(C_{2\alpha}\) 变形可得升幂公式 \(1+\cos\alpha=2\cos^2\frac\alpha2,1-\cos\alpha=2\sin^2\frac\alpha2\)，降幂公式 \(\cos^2\alpha=\frac{1+\cos2\alpha}2,\sin^2\alpha=\frac{1-\cos2\alpha}2\)。

对降幂公式开根号，并用 \(\frac\alpha2\) 替换 \(\alpha\) 可得正弦、余弦的半角公式：\(\sin\frac\alpha2=\pm\sqrt{\frac{1-\cos\alpha}2},\cos\frac\alpha2=\pm\sqrt{\frac{1+\cos\alpha}2}\)。两式相除可得 \(\tan\frac{\alpha}2=\pm\sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}}\)。有理化一下得到 \(\tan\frac\alpha2=\frac{1-\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos\alpha}\)。其中正负视 \(\frac\alpha2\) 的象限而定。

取出两个相对的和角、差角公式求和或作差，如 \(C_{\alpha+\beta}\) 加上 \(C_{\alpha-\beta}\)，得 \(\cos\alpha\cos\beta=\frac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\)。这是积化和差公式。

类似地，有四个积化和差公式：

\[\begin{aligned}\sin\alpha\cos\beta&=\frac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\\cos\alpha\sin\beta&=\frac12[\sin(\alpha+\beta)-\sin(\alpha-\beta)]\\\cos\alpha\cos\beta&=\frac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\\\sin\alpha\sin\beta&=\frac12[\cos(\alpha+\beta)-\cos(\alpha-\beta)]\\\end{aligned} \]

反过来，可以得到积化和差公式：

\[\begin{aligned}\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}2\cos\frac{\alpha-\beta}2\\\sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}2\sin\frac{\alpha-\beta}2\\\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}2\cos\frac{\alpha-\beta}2\\\cos\alpha+\cos\beta=2\sin\frac{\alpha+\beta}2\sin\frac{\alpha-\beta}2\\\end{aligned} \]

有一个神奇的东西叫万能公式，可以将三角函数变成 \(\tan\frac\alpha2\) 的形式。

\[\begin{aligned}\sin\alpha=\frac{2\sin\frac\alpha2\cos\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2}=\frac{2\tan\frac\alpha2}{1+\tan^2\frac\alpha2}\\\cos\alpha=\frac{\cos^2\frac\alpha2-\sin^2\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2}=\frac{1-\tan^2\frac\alpha2}{1+\tan^2\frac\alpha2}\\\tan\alpha=\frac{\frac{2\tan\frac\alpha2}{1+\tan^2\frac\alpha2}}{\frac{1-\tan^2\frac\alpha2}{1+\tan^2\frac\alpha2}}=\frac{2\tan\frac\alpha2}{1-\tan^2\frac\alpha2}\end{aligned} \]

若连用两次二倍角公式，可得三倍角公式：

\[\begin{aligned}\sin3\alpha=3\sin\alpha-4\sin^3\alpha=4\sin\alpha\sin(\frac\pi3+\alpha)\sin(\frac\pi3-\alpha)\\\cos3\alpha=4\cos^3\alpha-3\cos\alpha=4\cos\alpha\cos(\frac\pi3+\alpha)\cos(\frac\pi3-\alpha)\\\tan3\alpha=-\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^3\alpha}=\tan\alpha\tan(\frac\pi3+\alpha)\tan(\frac\pi3-\alpha)\end{aligned} \]

[[数学]]