博弈论 学习笔记

定义

博弈论主要研究的是：在一个游戏中，进行游戏的多位玩家的策略。

OI 中出现比较多的是公平组合游戏，满足几点性质：

• 游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；

• 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；

• 游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

一个简单的公平组合游戏：Nim 游戏，有若干堆石子，双方可以轮流从一堆石子中取任意个石子。无石子取的一方输。

策梅洛定理

根据策梅洛定理，这样的游戏中的任何一个状态，要么先手有必胜策略，要么后手有必胜策略。

因此把所有状态分为两种：必胜态和必败态，分别表示面对这个状态的一方必胜或者必败。显然，没有后继状态时可以根据规则确定状态（一般是必败态，是必胜态的称为反常游戏）。而一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态，一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。

可以把状态看作点，状态的转移看作边，建一张有向图。比如下面是 Nim 游戏中两堆一个石子的有向图。

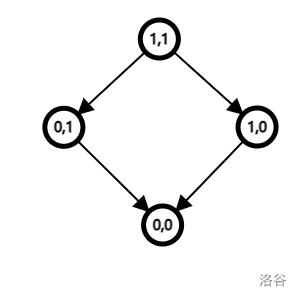
根据定义，\(0,0\) 必败，\(0,1\) 和 \(1,0\) 必胜，\(1,1\) 必败。

SG函数

引入一个运算 \(\operatorname{mex}\{S\}=\min\{x\}(x\notin S,x\in N)\)，表示一个集合 \(S\) 内未出现的最小非负整数。

定义 \(\operatorname{SG}(A)=\operatorname{mex}\{\operatorname{SG}(B)\mid A\to B\}\)。这里的 \(A,B\) 都是游戏中的一种状态。这个函数表示状态 \(A\) 能转移到的状态中未出现的最小值。那么 \(SG\) 为 \(0\) 是必败态，否则为必胜态。

Sprague-Grundy 定理：\(n\) 个游戏的组合，设状态分别为 \(s_1,s_2,\cdots,s_n\)，当且仅当 \(\operatorname{xor}_{i=1}^n\operatorname{SG}(s_i)\ne 0\) 时为必胜态。

一堆的 Nim 游戏中 \(\operatorname{SG}(A)=A\)。那么根据 SG 定理可得 Nim 游戏的结论：当石子个数异或为 \(0\)，后手必胜，否则先手必胜。

证明

定义状态 \(A,B\) 的组合为 \(A+B\)，观察组合状态的 \(\operatorname{SG}\) 函数的性质。

有 \(\operatorname{SG}(A)=\operatorname{SG}(B)\) 时 \(\operatorname{SG}(A+B)=0\)，\(\operatorname{SG}(A)\ne\operatorname{SG}(B)\) 时 \(\operatorname{SG}(A+B)\ne0\)。因为当两个状态的 \(\operatorname{SG}\) 相同时，先走者如果降低其中一个的 \(\operatorname{SG}\)，后手可以同时降低另一堆，保持 \(\operatorname{SG}\) 相同，最终会变成两个必败态。如果增加，后手可以降回来。

一个状态和必败态组合，\(\operatorname{SG}\) 不变，因为必败态不能变化。

枚举两个状态的 \(\operatorname{SG}\) 不同的情况：

\(\operatorname{SG}(1+2)=3,\operatorname{SG}(1+3)=2,\operatorname{SG}(2+3)=1\cdots\)

枚举了几组后，发现全都符合异或的性质，包括上面的两条规律也是异或的规律。

更加严谨的证明需要数学归纳法。首先必败态的组合满足 SG 定理，即证当一个状态满足 SG 定理，其前驱也满足定理。

将 SG 定理代入：\(\operatorname{SG}(A+B)=\operatorname{mex}(\{\operatorname{SG}(C)\operatorname{xor}\operatorname{SG}(B)\mid A\to C\}\cup\{\operatorname{SG}(D)\operatorname{xor}\operatorname{SG}(A)\mid D\to B\})\)

\(\operatorname{SG}(A)\operatorname{xor}\operatorname{SG}(B)\) 不会属于后面的两个集合，因为 \(A\ne C,B\ne D\)。

对于 \(\forall e<\operatorname{SG}(A)\operatorname{xor}\operatorname{SG}(B)\)，\(\operatorname{SG}(C)=e\operatorname{xor}\operatorname{SG}(B),\operatorname{SG}(D)=e\operatorname{xor}\operatorname{SG}(A)\)。有 \(e\operatorname{xor}\operatorname{SG}(B)\ne\operatorname{SG}(A),e\operatorname{xor}\operatorname{SG}(A)\ne\operatorname{SG}(B)\)。

假设 \(e\operatorname{xor}\operatorname{SG}(B)>\operatorname{SG}(A),e\operatorname{xor}\operatorname{SG}(A)>\operatorname{SG}(B)\)。那么两个式子异或得到 \(\operatorname{SG}(A)\operatorname{xor}\operatorname{SG}(B)>\operatorname{SG}(A)\operatorname{xor}\operatorname{SG}(B)\)，矛盾。因此有\(e\operatorname{xor}\operatorname{SG}(B)<\operatorname{SG}(A)\vee e\operatorname{xor}\operatorname{SG}(A)<\operatorname{SG}(B)\)，即 \(e\) 属于两个集合之一。根据 \(\operatorname{mex}\) 的定义，\(\operatorname{SG}(A+B)=\operatorname{SG}(A)\operatorname{xor}\operatorname{SG}(B)\)。

常见模型

巴什博弈

有 \(n\) 个石子，双方轮流取 \([1,m]\) 个石子。无石子取的一方输。

结论：\(m+1\mid n\) 时后手有必胜策略，否则先手有必胜策略。

证明：

当 \(n\leq m\)，显然先手必胜。因此 \(n=m+1\) 是必败态。

当 \(m+1\mid n\)，先手取多少个，后手可以使取的石子数与先手的和为 \(m+1\)，使 \(m+1\mid n\)，最后先手面对 \(n=m+1\)。当 \(m+1\nmid n\)，先手就可以取 \(n\bmod (m+1)\)。

Nim 游戏

有若干堆石子，双方可以轮流从一堆石子中取任意个石子。无石子取的一方输。

结论：当石子个数异或为 \(0\)，后手必胜，否则先手必胜。

证明见前文。

威佐夫博弈

有两堆石子，分别有 \(n,m(n<m)\) 个。双方轮流从一堆石子中取任意个石子或从两堆中取相同数量的石子。无石子取的一方输。

结论：当 \(n=\lfloor\frac{\sqrt 5+1}{2}(m-n)\rfloor\)，后手有必胜策略，否则先手有必胜策略。

证明：

打表一下必败态，\((0,0),(1,2),(3,5),(4,7),(6,10),(8,13)\cdots\)，发现不算 \((0,0)\) 的第 \(k\) 个必败态中 \(n\) 为前面必败态的 \(\operatorname{mex}\)，\(m=n+k\)。

如果此时先手取石子少的一堆或取两堆，因为 \(n\) 为前面必败态的 \(\operatorname{mex}\)，取后的 \(n\) 在必败态中出现，后手可以降低另一堆；

如果此时先手取石子多的一堆，那么此时 \(m-n\) 在之前的必败态出现，后手可以同时取两堆来到一个必败态。

分析必败态的性质，引入 Beatty 定理：对于两个正无理数 \(a,b\) 使 \(\frac{1}{a}+\frac{1}{b}=1\)，令 \(P=\{p\mid p=\lfloor an \rfloor,n\in \mathbb{N}^+\},Q=\{p\mid p=\lfloor bm \rfloor,m\in \mathbb{N}^+\}\)，有 \(P\cap Q=\varnothing,P\cup Q=\mathbb{N}^+\)。

Beatty 定理的证明：

反证，假设存在 \(k\in \mathbb{N}^+,k\in P,k\in Q\)。

\(\because a,b\in\complement_\mathbb{R}\mathbb{Q}\)

\(\therefore an,bm\notin \mathbb{N}^+,k<an<k+1,k<bm<k+1\)

\(\frac{n}{k+1}<\frac{1}{a}<\frac{n}{k},\frac{m}{k+1}<\frac{1}{b}<\frac{m}{k}\)

两式相加得 \(\frac{n+m}{k+1}<\frac{1}{a}+\frac{1}{b}=1<\frac{n+m}{k}\) 即 \(k<n+m<k+1\)，与 \(n,m,k\in \mathbb{N}^+\) 矛盾。

同理反证，假设存在 \(k\in \mathbb{N}^+,k\notin P,k\notin Q\)。

\(an<k<k+1<a(n+1),bm<k<k+1<b(m+1)\)

\(\frac{n}{k}<\frac{1}{a}<\frac{n+1}{k+1},\frac{m}{k}<\frac{1}{b}<\frac{m+1}{k+1}\)

两式相加得 \(\frac{n+m}{k}<\frac{1}{a}+\frac{1}{b}=1<\frac{n+m+2}{k+1}\) 即 \(n+m<k<k+1<n+m+2\)，与 \(n,m,k\in \mathbb{N}^+\) 矛盾。

定理得证。

返回上面，令 \(n=\lfloor ak\rfloor,m=\lfloor (a+1)k\rfloor\)。有 \(\frac{1}{a}+\frac{1}{a+1}=1\)，解得 \(a=\frac{\sqrt 5+1}{2}\)，\(n=\lfloor ak\rfloor=\lfloor\frac{\sqrt 5+1}{2}(m-n)\rfloor\)。

[[数学]]