字典树 学习笔记

普通字典树

概述

字典树（Trie）是一种数据结构，一般用于处理字符串问题与异或问题。

字典树的结构是这样的：

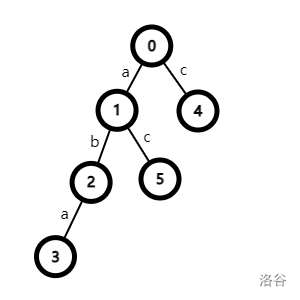
其中每一个字符就是字典树的边，比如 aba 就是 \(0\to1\to2\to3\)，ac 是 \(0\to1\to5\)。而其中的节点代表的是字符串的前缀。

字典树的主体可以用一个数组 \(tr_{i,j}\)，表示第 \(i\) 个节点经过字符 \(j\)（需要将字符集映射成数字） 的边到达的点。

插入

从根节点开始走，如果能共用边就往下走，否则就新开节点。

int to_num(char c){
  return c-'a';
}
void insert(string a,int pos=0){
  for(int i=0;i<a.size();i++){
    int t=to_num(a[i]);
    if(!tr[pos][t])tr[pos][t]=++cnt;
    pos=tr[pos][t];
  }
  vis[pos]=1;
}

这里的 \(vis\) 表示这个节点是不是字符串的末尾，在查询时用到。字典树中常用字符串末尾的叶节点指代一个字符串。

查询

同样从根节点往下走，如果下一个节点没有就说明没有这个字符串。

如果走到了字符串末尾，返回 \(vis\) 而非直接返回真。如果 \(vis\) 为假，说明查询的串是其中一个串的前缀。比如查询 ab，有一个串 abcde，也是能走完的，但是 \(ab\) 并没有出现过。

代码：

bool query(string a,int pos=0){
  for(int i=0;i<a.size();i++){
    int t=to_num(a[i]);
    if(!tr[pos][t])return 0;
    pos=tr[pos][t];
  }
  return vis[pos];
}

01字典树

正序建树

插入、删除

如果把一个数的二进制看作字符串，可以构建一个字符集为 \(\{0,1\}\) 的字典树，称为01字典树（01-trie）。

插入的过程类似普通字典树。另外用一个 \(vis\) 表示当前节点到父亲的边走了多少次。

void insert(int a,int pos=0){
  for(int i=1<<maxd;i>0;i>>=1){
    bool t=a&i;
    if(!tr[pos][t])tr[pos][t]=++cnt;
    pos=tr[pos][t],vis[pos]++;
  }
}

删除与查询类似，将沿途的 \(vis\) 都减一即可。

void erase(int a,int pos=0){
  for(int i=1<<maxd;i>0;i>>=1){
    bool t=a&i;
    pos=tr[pos][t],vis[pos]--;
  }
}

查询异或极值

01字典树多用于异或问题，可以是查询异或极值，即给定一堆数，问查询的数与这些数中哪个异或起来最大。

考虑贪心，从最高位开始在字典树上跳，尽量走与当前的位相反的方向即可。

int query(int a,int pos=0,int ans=0){
  for(int i=1<<maxd;i>0;i>>=1){
    bool t=a&i;
    if(tr[pos][!t]&&vis[tr[pos][!t]])pos=tr[pos][!t],ans+=i;
    else pos=tr[pos][t];
  }
  return ans;
}

倒序建树

pushup

从低位往高位建树可以维护不同的信息，比如支持查询全局异或和，全局加一。

维护两个数组 \(v,w\)，分别表示子树异或和、子树叶节点个数的奇偶性。类似线段树，有一个用子节点更新当前节点的函数：

void pushup(int pos){
  w[pos]=v[pos]=0;
  if(tr[pos][0])w[pos]^=w[tr[pos][0]],v[pos]^=v[tr[pos][0]]<<1;
  if(tr[pos][1])w[pos]^=w[tr[pos][1]],v[pos]^=(v[tr[pos][1]]<<1)|w[tr[pos][1]];
}

对于 \(w\)，直接将子树相加即可。当前节点的 \(v\) 异或上左右子树的 \(v\)。由于从低位往高位建树，左右儿子的 \(v\) 要左移一位。当前节点往右儿子的边会产生 \(0\) 或 \(1\) 的贡献，应单独算。

那么全局异或和就是根节点的 \(v\)。

查询、删除

由于 pushup 的存在，递归会好写一点。

void insert(int a,int &pos,int d){
  if(!pos)pos=++cnt;
  if(d>maxd)w[pos]^=1;
  else insert(a>>1,tr[pos][a&1],d+1),pushup(pos);
}
void erase(int a,int pos,int d){
  if(d>maxd)w[pos]^=1;
  else erase(a>>1,tr[pos][a&1],d+1),pushup(pos);
}

全局加一

对一个数加一，二进制上会把最低位的零与更低位翻转。放到字典树上就是交换左右儿子然后沿着走零的边。

void add(int pos){
  swap(tr[pos][0],tr[pos][1]);
  if(tr[pos][0])add(tr[pos][0]);
  pushup(pos);
}

[[数据结构]]