平衡树 学习笔记
定义
二叉查找树是一种树形数据结构,支持动态插入删除,查询排名和第 k 小,查询前驱后继等。二叉查找树的点权满足左儿子小于当前节点小于右儿子。上面的这些操作都可以在树上二分解决。
但是当树的深度很大,接近一条链时,操作复杂度会退化至 \(O(n)\),于是有了各种方法使树的深度保持期望 \(O(\log n)\),也就是各种平衡树。
有旋 Treap
定义
Treap 是一种笛卡尔树,其中点权满足二叉查找树的性质,再给每个点一个随机的权,维护这个值的堆性质。这就使得树的性质足够强,保证了期望 \(O(log n)\) 的复杂度。
Treap 的每个点维护基本信息:点权、左右儿子、每个节点代表的数的个数、子树大小、随机权值。
pushup
通过儿子的子树大小更新当前节点的子树大小。
void pushup(int pos){
sz[pos]=sz[tr[pos][0]]+sz[tr[pos][1]]+num[pos];
}
旋转
有旋 Treap 通过旋转维护堆性质。旋转是一个重要的操作,还有其他一些类型的平衡树使用旋转。
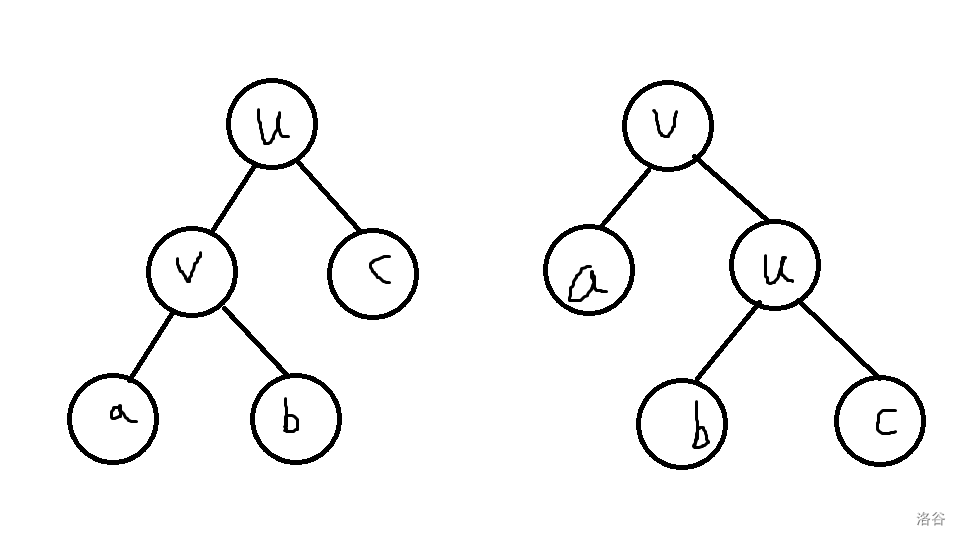
如图,要让 \(u\) 的左儿子 \(v\) 变成这棵子树的根,同时不破坏二叉查找树的性质。将 \(u\) 及其右子树变成 \(v\) 的右儿子,原来 \(v\) 的右子树接到 \(u\) 的左子树上,变为右图,这就是右旋。左旋方向相反,与右旋是互逆操作。
void rotate(int &pos,bool d){
int temp=tr[pos][!d];
tr[pos][!d]=tr[temp][d],tr[temp][d]=pos,pushup(pos),pushup(temp),pos=temp;
}
这样做,树的中序遍历没有变化,但是 \(u,v\) 的父子关系变化了。
插入
首先一路递归到叶节点或空节点插入。在回溯时,如果递归方向的随机权值不再满足堆的性质,就要旋转。然后一路 pushup。
void insert(int &pos,T k){
if(!pos){
pos=++cnt,v[pos]=k,num[pos]=sz[pos]=1,r[pos]=rand();
return;
}
if(k==v[pos]){
num[pos]++,sz[pos]++;
return;
}
bool d=k>v[pos];
insert(tr[pos][d],k);
if(r[pos]<r[tr[pos][d]])rotate(pos,!d);
pushup(pos);
}
删除
删除时如果直接删掉非叶节点,就会破坏掉树的结构。这时通过旋转把要删除的节点旋下去,让随机权值较大的子节点顶替位置,到叶子再删。
void erase(int &pos,T k){
if(!pos)return;
if(k==v[pos]){
if(!tr[pos][0]&&!tr[pos][1]){
num[pos]--,sz[pos]--;
if(!num[pos])pos=0;
}
else if(tr[pos][0]&&!tr[pos][1])rotate(pos,1),erase(tr[pos][1],k);
else if(!tr[pos][0]&&tr[pos][1])rotate(pos,0),erase(tr[pos][0],k);
else{
bool d=r[tr[pos][0]]>r[tr[pos][1]];
rotate(pos,d),erase(tr[pos][d],k);
}
}
else erase(tr[pos][k>v[pos]],k);
pushup(pos);
}
询问排名
若查询值小于当前节点的点权,则当前位置没有贡献,向左递归;
若查询值等于当前节点的点权,则当前节点的排名为左子树的大小加一;
若查询值大于当前节点的点权,向右递归,答案加上左子树与这个节点的大小;
若节点不存在,根据排名的定义,返回 \(1\)。
int rank(int pos,T k){
if(!pos)return 1;
if(k<v[pos])return rank(tr[pos][0],k);
else if(k==v[pos])return sz[tr[pos][0]]+1;
else return sz[tr[pos][0]]+num[pos]+rank(tr[pos][1],k);
}
询问第 k 小
若 \(k\) 不大于左子树的大小,则答案在左子树中,向左递归;
若 \(k\) 大于左子树与当前节点的大小,向右递归,\(k\) 减去左子树与当前节点的大小。
如果两种都不是,说明答案就是当前节点。
T kth(int pos,int k){
if(!pos)return 0;
if(k<=sz[tr[pos][0]])return kth(tr[pos][0],k);
else if(k>sz[tr[pos][0]]+num[pos])return kth(tr[pos][1],k-sz[tr[pos][0]]-num[pos]);
else return v[pos];
}
询问前驱后继
查询前驱时,如果 \(x\) 小于等于当前节点,则向左寻找答案;否则向右走,得到的答案与当前节点的值取 \(\max\)。后继类似。
T prev(int pos,T k){
if(!pos)return -inf;
if(k<=v[pos])return prev(tr[pos][0],k);
else return max(v[pos],prev(tr[pos][1],k));
}
T next(int pos,T k){
if(!pos)return inf;
if(k>=v[pos])return next(tr[pos][1],k);
else return min(v[pos],next(tr[pos][0],k));
}
Splay
定义
Splay 树通过 Splay 操作保证一次操作复杂度为均摊 \(O(\log n)\)。Splay 要多存一个父节点。
pushup
同 Treap。
get
判断当前节点是右儿子还是左儿子。
bool get(int pos){
return tr[f[pos]][1]==pos;
}
find
辅助操作,在树上寻找一个节点。
int find(int pos,T k){
while(k!=v[pos])pos=tr[pos][k>v[pos]];
return pos;
}
旋转
Splay 的旋转与 Treap 的有不同:Splay 的旋转是在旋上去的子节点的角度看,而 Treap 是原来的父节点的角度。
void rotate(int pos){
int f1=f[pos],f2=f[f1];
bool d=get(pos);
tr[f1][d]=tr[pos][d^1],f[tr[f1][d]]=f1,tr[f2][get(f1)]=pos,f[pos]=f2,tr[pos][d^1]=f1,f[f1]=pos,pushup(f1),pushup(pos);
}
可以发现,每次旋转,旋转的对象会上移一个深度。
Splay 操作
Splay 操作通过将一个节点上旋到某个位置(一般为根)来保证复杂度。
一个简单的办法是每次单旋,让节点上移一层,最后 Spaly 到根。这样的复杂度是假的:
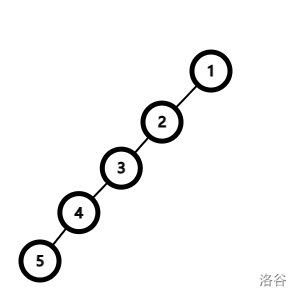
这是一条链。
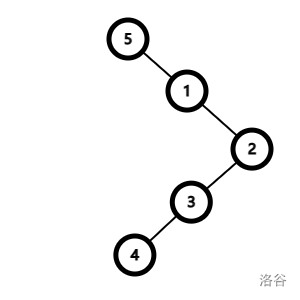
这是把 \(5\) 单旋到根后的链。发现这还是一条链,不太平衡,很容易被卡。
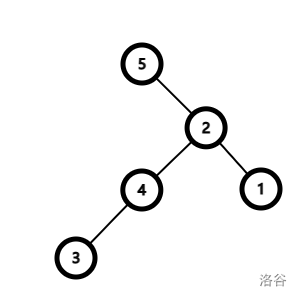
正确的做法是双旋,把两次旋转一起考虑。当节点与父节点旋转的方向相同,应先旋父节点再旋当前节点,这样有利于树的平衡。
插入
找到插入的位置,然后要把新节点 Splay 到根。由于在 Splay 同时也 pushup 了,可以不递归。
void insert(int &rt,T k){
int pos=rt,p=0;
while(pos&&k!=v[pos])p=pos,pos=tr[pos][k>v[pos]];
if(pos)num[pos]++;
else{
pos=++cnt,v[pos]=k,f[pos]=p,num[pos]=sz[pos]=1;
if(p)tr[p][k>v[p]]=pos;
}
splay(pos,rt);
}
删除
先将代表这个数的节点 Splay 到根。如果个数大于一就退出,否则删除节点后还要合并左右两棵子树。
特判掉左右子树缺失的情况。若左右子树完整,应将左子树内最大的节点 Splay 成新的根,再接上右子树。
void erase(int &rt,T k){
splay(find(rt,k),rt);
if(num[rt]>1)num[rt]--,pushup(rt);
else{
if(!tr[rt][0]&&!tr[rt][1])rt=0;
else if(!tr[rt][0]&&tr[rt][1])rt=tr[rt][1],f[rt]=0;
else if(tr[rt][0]&&!tr[rt][1])rt=tr[rt][0],f[rt]=0;
else{
int pos=tr[rt][0];
while(tr[pos][1])pos=tr[pos][1];
splay(pos,tr[rt][0]),tr[pos][1]=tr[rt][1],f[tr[rt][1]]=pos,f[pos]=0,pushup(pos),rt=pos;
}
}
}
询问排名
将这个节点 Splay 到根后答案就是左子树大小加一。
int rank(int &rt,T k){
return splay(find(rt,k),rt),sz[tr[rt][0]]+1;
}
询问第 K 小
仿照 Treap 遍历整棵树。最后要把节点 Splay 到根。
T kth(int &rt,int k){
int pos=rt;
while(1){
if(k<=sz[tr[pos][0]])pos=tr[pos][0];
else{
k-=sz[tr[pos][0]]+num[pos];
if(k<=0)return splay(pos,rt),v[pos];
pos=tr[pos][1];
}
}
}
询问前驱后继
首先插入询问的数。此时这个数为根,前驱为左子树中最大的值,后继为右子树中最小的。
T prev(int &rt,T k,T ans=0){
insert(rt,k);
int pos=tr[rt][0];
while(tr[pos][1])pos=tr[pos][1];
return splay(pos,rt),ans=v[pos],erase(rt,k),ans;
}
T next(int &rt,T k,T ans=0){
insert(rt,k);
int pos=tr[rt][1];
while(tr[pos][0])pos=tr[pos][0];
return splay(pos,rt),ans=v[pos],erase(rt,k),ans;
}
区间操作
Splay 可以维护区间信息。
换一种方式建树,将节点按照下标排序而非权值排序。树的中序遍历为原序列。每个节点代表子树的区间(由于平衡树的性质,子树对应的下标连续)。
对于每个节点维护当前节点的信息与子树的信息和。相比线段树,Splay pushup 时要加上节点本身的信息。
void pushup(int pos){
sz[pos]=sz[tr[pos][0]]+sz[tr[pos][1]]+1,sum[pos]=sum[tr[pos][0]]+sum[tr[pos][1]]+v[pos];
}
void build(int &pos,int nl,int nr,int fa,T a[]){
if(nl>nr)return;
int mid=(nl+nr)>>1;
pos=++cnt,v[pos]=a[mid],f[pos]=fa;
build(tr[pos][0],nl,mid-1,pos,a),build(tr[pos][1],mid+1,nr,pos,a),pushup(pos);
}
在树上,下标 \(k\) 对应的节点为树上第 \(k\) 个,用上面查询第 K 小的方式即可。
T kth(int &rt,int k){
int pos=rt;
while(1){
if(k<=sz[tr[pos][0]])pos=tr[pos][0];
else{
k-=sz[tr[pos][0]]+1;
if(k<=0)return pos;
pos=tr[pos][1];
}
}
}
区间操作时,先把操作区间提取出来。根据平衡树的性质,把 \(l-1\) Splay 到根,\(r+1\) Splay 到 \(l-1\) 的右子树上,\(r+1\) 的左子树就是操作区间。
Splay 区间修改也可以像线段树一样打标记。区间查询直接取出区间的值即可,因为在 Splay 操作的过程中已经维护了值。
void pushdown(int pos){
tag[tr[pos][0]]+=tag[pos],tag[tr[pos][1]]+=tag[pos];
v[tr[pos][0]]+=tag[pos],v[tr[pos][1]]+=tag[pos];
sum[tr[pos][0]]+=sz[tr[pos][0]]*tag[pos],sum[tr[pos][1]]+=sz[tr[pos][1]]*tag[pos];
tag[pos]=0;
}
void rotate(int pos){
int f1=f[pos],f2=f[f1];
bool d=get(pos);
pushdown(f1),pushdown(pos),tr[f1][d]=tr[pos][d^1],f[tr[f1][d]]=f1,tr[f2][get(f1)]=pos,f[pos]=f2,tr[pos][d^1]=f1,f[f1]=pos,pushup(f1),pushup(pos);
}
void splay(int pos,int &rt){
for(int temp=f[rt];f[pos]!=temp;rotate(pos))if(f[f[pos]]!=temp)rotate(get(pos)==get(f[pos])?f[pos]:pos);
rt=pos;
}
void add(int &rt,int l,int r,T k){
splay(kth(rt,l-1),rt),splay(kth(rt,r+1),tr[rt][1]);
v[tr[tr[rt][1]][0]]+=k,tag[tr[tr[rt][1]][0]]+=k,sum[tr[tr[rt][1]][0]]+=sz[tr[tr[rt][1]][0]]*k;
}
T query(int &rt,int l,int r){
return splay(kth(rt,l-1),rt),splay(kth(rt,r+1),tr[rt][1]),sum[tr[tr[rt][1]][0]];
}
Splay 的结构还使它可以做到区间翻转,相当于翻转左右子树。
void pushdown(int pos){
if(tag[pos])swap(tr[pos][0],tr[pos][1]),tag[tr[pos][0]]^=1,tag[tr[pos][1]]^=1,tag[pos]=0;
}
此外,在查询第 K 小时要下传标记,因为下传标记时树的形态会改变。
FHQ Treap
定义
FHQtreap 是一种 Treap,不依赖旋转维护随机权值堆性质,而是通过分裂和合并,具有码量小,好理解,支持区间操作和可持久化等优势。
FHQtreap 将相同权值存在不同的节点。
按值分裂
这个操作会将树分裂成小于等于 \(k\) 的数 \(A\) 和大于 \(k\) 的树 \(B\)。
如果当前节点小于等于 \(k\),则 \(k\) 及 \(k\) 的左子树属于 \(A\),将这个位置赋给 \(A\) 的引用,然后递归右子树。大于 \(k\) 则相反。当节点为空时 \(A,B\) 赋值 \(0\),此时 \(A\) 或 \(B\) 表示连接两棵树的边,这样就断开了连接。
void split1(int pos,T k,int &a,int &b){
if(!pos){
a=b=0;
return;
}
if(v[pos]<=k)a=pos,split1(tr[pos][1],k,tr[a][1],b);
else b=pos,split1(tr[pos][0],k,a,tr[b][0]);
pushup(pos);
}
按排名分裂
类似按值分裂,不过递归到右子树要减去左子树与当前节点的大小。
void split2(int pos,int k,int &a,int &b){
if(!pos){
a=b=0;
return;
}
if(sz[tr[pos][0]]<k)a=pos,split2(tr[pos][1],k-sz[tr[pos][0]]-1,tr[a][1],b);
else b=pos,split2(tr[pos][0],k,a,tr[b][0]);
pushup(pos);
}
合并
合并操作要求第一棵树的权值小于等于第二棵树。
类似线段树合并,如果两棵树有一颗递归到空,就返回另一个节点。在合并时要满足堆性质,若 \(a\) 的随机权值小于 \(b\) 的随机权值,就取 \(a\) 的节点,把 \(b\) 的节点放进子树里递归。由于 \(a<b\),进入右子树。另一种情况类似。
int merge(int a,int b){
if(!a||!b)return a^b;
if(r[a]<r[b])return tr[a][1]=merge(tr[a][1],b),pushup(a),a;
else return tr[b][0]=merge(a,tr[b][0]),pushup(b),b;
}
插入
按 \(k\) 裂出两棵树,把创建的新节点作为一棵树,顺次合并三棵树。
void insert(int &rt,T k,int a=0,int b=0){
split1(rt,k,a,b),v[++cnt]=k,sz[cnt]=1,r[cnt]=rand(),rt=merge(merge(a,cnt),b);
}
删除
以 \(k-1,k\) 裂出三棵树,中间的树权值为 \(k\),删掉根后合并形成的四棵树。
void erase(int &rt,T k,int a=0,int b=0,int c=0){
split1(rt,k-1,a,b),split1(b,k,b,c),rt=merge(merge(a,merge(tr[b][0],tr[b][1])),c);
}
询问排名
裂出小于等于 \(k-1\) 的树,排名为树大小加一。
int rank(int &rt,T k,int a=0,int b=0,int ans=0){
return split1(rt,k-1,a,b),ans=sz[a]+1,rt=merge(a,b),ans;
}
询问第 K 小
按排名裂出第 K 小和小于,大于排名的三棵树,中间的树的值为第 K 小。
T kth(int &rt,int k,int a=0,int b=0,int c=0,int ans=0){
return split2(rt,k-1,a,b),split2(b,1,b,c),ans=v[b],rt=merge(merge(a,b),c),ans;
}
询问前驱后继
询问前驱时先裂出小于 \(k\) 的树,再查询这棵树中排名最大的数。后驱类似。
T prev(int &rt,T k,int a=0,int b=0,int c=0,int ans=0){
return split1(rt,k-1,a,c),split2(a,sz[a]-1,a,b),ans=v[b],rt=merge(merge(a,b),c),ans;
}
T next(int &rt,T k,int a=0,int b=0,int c=0,int ans=0){
return split1(rt,k,a,b),split2(b,1,b,c),ans=v[b],rt=merge(merge(a,b),c),ans;
}
区间操作
同样建出区间树。操作区间时,裂出排名介于 \(l,r\) 之间的树进行操作。
void reverse(int &rt,int l,int r,int a=0,int b=0,int c=0){
split(rt,l-1,a,b),split(b,r-l+1,b,c),tag[b]^=1,rt=merge(merge(a,b),c);
}
分裂合并时应在递归之前下传标记,因为递归需要原来的结构。
void split(int pos,int k,int &a,int &b){
if(!pos){
a=b=0;
return;
}
pushdown(pos);
if(k<=sz[tr[pos][0]])b=pos,split(tr[pos][0],k,a,tr[b][0]);
else a=pos,split(tr[pos][1],k-sz[tr[pos][0]]-1,tr[a][1],b);
pushup(pos);
}
int merge(int a,int b){
if(!a||!b)return a^b;
if(r[a]<r[b])return pushdown(a),tr[a][1]=merge(tr[a][1],b),pushup(a),a;
else return pushdown(b),tr[b][0]=merge(a,tr[b][0]),pushup(b),b;
}
[[数据结构]]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号