划分树 学习笔记

建树

划分树（Dividing Tree）是一种可以解决静态区间 kth 的数据结构，与主席树相比更好理解，常数也更小。缺点是适用范围小，基本专门用来求解这个问题。下面以第 k 小为例。

划分树的结构如下：

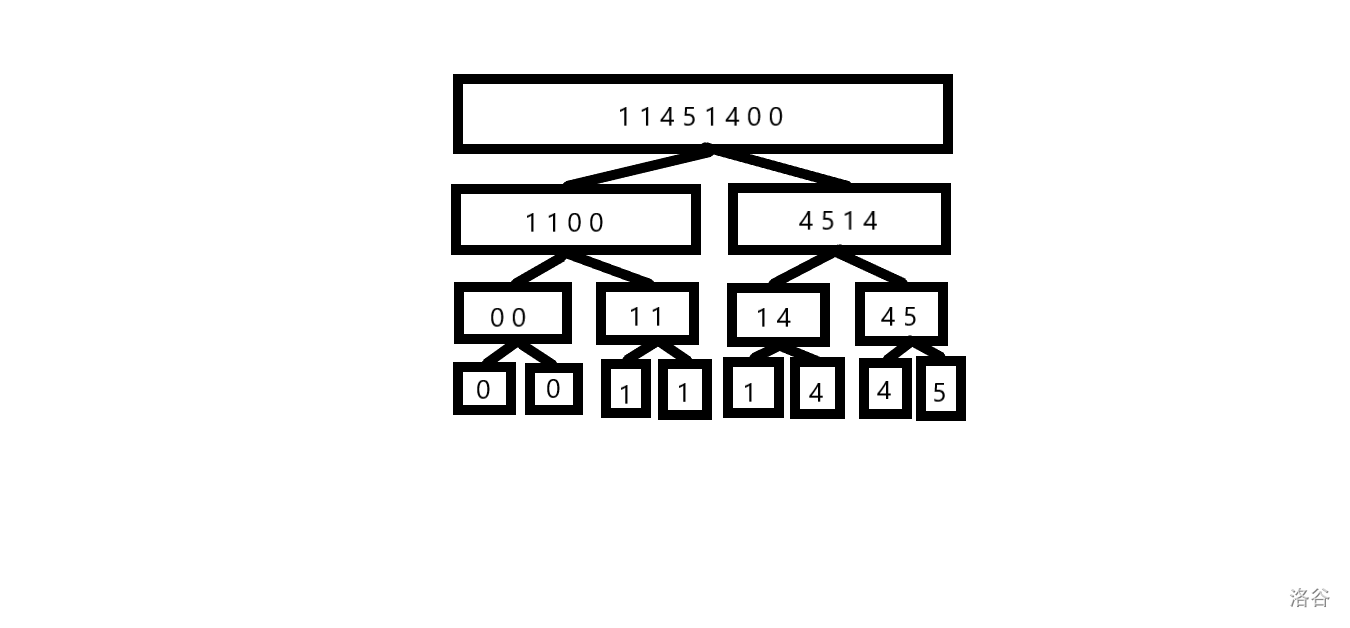
方便起见，将原数组的长度补成 \(2\) 的整数幂。划分树的每个节点都是一个数组，根节点为原数组，节点的左右儿子这个节点的子序列，长度为这个节点的一半，且满足左儿子里面的值均不大于右儿子。

划分树的每一层可以看作对原数组进行快排的中间过程。

建树时，找出当前节点的中位数，小于中位数的放左边，大于中位数的放右边，中位数填空。

划分树的性质说明，对一个结点代表的数组排序，对应到排序后的原数组位置不变，因此求中位数可以只对原数组排序。

在排序时顺便求出一个辅助数组 \(cnt_{i,j}\) 表示第 \(j\) 层划分到左儿子的前缀和，在查询时要用。

代码：

for(num=1,d=0;num<n;num<<=1,d++);
for(int i=1;i<=n;i++)tr[i][0]=temp[i]=a[i];
sort(temp+1,temp+num+1);
for(int i=0,w=num;i<=d;i++,w>>=1){
  for(int j=1;j<=num;j+=w){
    T mid=temp[j+(w>>1)-1];
    int r=w>>1;
    for(int k=j;k<j+w;k++)if(tr[k][i]<mid)r--;
    for(int k=j,lpos=j,rpos=j+(w>>1);k<j+w;k++){
      if(k>j)cnt[k][i]=cnt[k-1][i];
      if(tr[k][i]<mid||(tr[k][i]==mid&&r-->0))tr[lpos++][i+1]=tr[k][i],cnt[k][i]++;
      else tr[rpos++][i+1]=tr[k][i];
    }
  }
}

查询

设查询的是 \([l,r]\) 的第 \(k\) 小，当前区间的起始位置为 \(pos\)。

首先求四个值 \(l_1,l_2,r_1,r_2\)，分别表示 \([1,l-1]\) 划分到左侧的个数，\([1,r]\) 划分到左侧的个数，\([1,l-1]\) 划分到右侧的个数，\([1,r]\) 划分到右侧的个数。

如果 \([l,r]\) 划分到左侧的个数 \(l_2-l_1\geq k\)，根据左侧的数小于等于右侧，可以得出第 k 小在左侧，否则在右侧。

转移到左侧时，原来的查询区间对应到左侧，变为划分到左侧的数对应的区间，因此 \(l\gets pos+l_1,r\gets pos+l_2-1\)。

转移到右侧时，查询区间同理变为划分到右侧的数对应的区间，有 \(l\gets pos+r_1,r\gets pos+r_2-1\)。并且已知 \(l_2-l_1\) 个数在左侧，有 \(k\gets k-(l_2-l_1)\)。起始下标也要变化。

代码：

if(k<1||k>r-l+1)return 0;
for(int i=0,pos=1,l1,l2,r1,r2;i<=d;i++){
  l1=(l==pos?0:cnt[l-1][i]),l2=cnt[r][i],r1=l-pos-l1,r2=r-pos-l2+1;
  if(l2-l1>=k)l=pos+l1,r=pos+l2-1;
  else pos+=(num>>(i+1)),l=pos+r1,r=pos+r2-1,k=k+l1-l2;
}
return tr[l][d];

[[数据结构]]