并查集 学习笔记
概述
并查集是一种维护集合的数据结构,可以看作一个森林,其中每个森林都代表一个集合。
操作
初始化
初始时每个元素单独一个集合。对于树的根节点,其父亲可以设为结点本身或 \(0\) 号结点。
我倾向于设为 \(0\) 号结点,这样可以省下这一步。
查询
查询一个结点的祖先时只需要不断向上跳即可。
int find(int x)
{
return f[x]?find(f[x]):x;
}
合并
并查集的主要思想是用一棵树的根代表整个集合。因此合并两个集合只需要把根节点之间连边即可。
bool merge(int u,int v){
int f1=find(u),f2=find(v);
return f1==f2?0:f[f1]=f2,1;
}
优化
路径压缩
一些极端情况下,不加优化的并查集会退化成链,这样每次查询的要调完整棵树。上面说过,一棵树的根代表整个集合,因此可以不看树的形态,直接把结点连到祖先,以减少树的深度。
具体实现时,在查询时顺便把结点往上连接即可。
int find(int x)
{
return f[x]?f[x]=find(f[x]):x;
}
启发式合并
在合并操作时,显然让规模更大的集合作为根更优,可以维护集合的深度或结点个数作为估价函数。
void build(int n){
for(int i=1;i<=n;i++)s[i]=1;
}
bool merge(int x,int y){
int f1=find(x),f2=find(y);
if(f1==f2)return 0;
if(s[f1]<s[f2])f[f1]=f2,s[f2]+=s[f1];
else f[f2]=f1,s[f1]+=s[f2];
return 1;
}
bool merge(int x,int y){
int f1=find(x),f2=find(y);
if(f1==f2)return 0;
if(d[f1]<d[f2])f[f1]=f2;
else{
f[f2]=f1;
if(d[f1]==d[f2])d[f1]++;
}
return 1;
}
时间复杂度
并查集的复杂度是个很玄学的东西。放一下 Tarjan 对并查集最劣复杂度的结论:
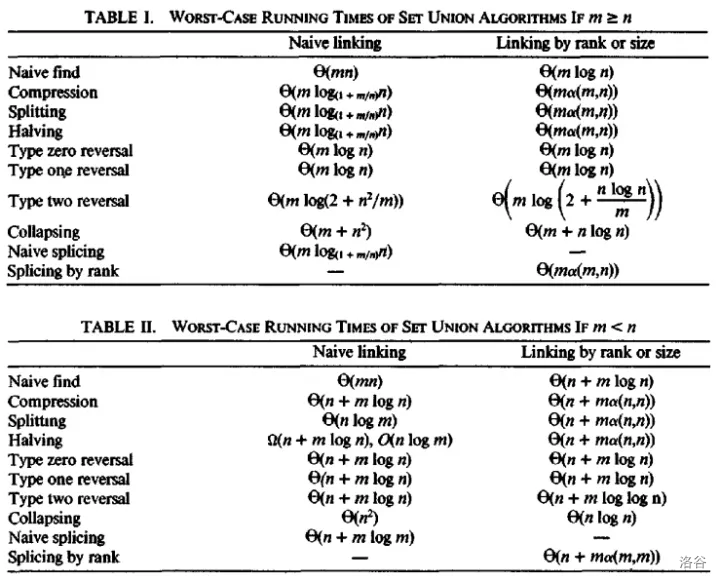
其中 \(m\) 为查询次数,\(n\) 为合并次数。
不加优化的并查集(naive find,naive linking)最劣是 \(\Theta(nm)\) 的,而且很容易卡,因此基本上会加优化。
单纯路径压缩(compression,naive linking)的最劣复杂度可近似看作 \(\Theta(m\log n)\),单纯启发式合并(naive find,linking by rank or size)的最劣复杂度是 \(\Theta(m\log n)\)。
两者并用的最劣复杂度为 \(\Theta(m\alpha(m,n))\)。其中 \(\alpha(m,n)\) 是一个增长很慢的函数,基本可以看作常数级。
路径压缩虽然简单,然而对树的结构破坏较大,因此有时不能使用。
拓展
带权并查集
在并查集中,还可以顺便维护点权。
以 P1196 为例:
维护 \(cnt\) 表示每个结点到队首的距离。合并时不能更改合并顺序,因为在后面的队伍的 \(cnt\) 要加上前面队伍的大小。
template<unsigned int maxn>struct DSU{
int f[maxn],s[maxn],cnt[maxn];
void build(int n){
for(int i=1;i<=n;i++)s[i]=1;
}
int find(int x)
{
if(!f[x])return x;
int temp=find(f[x]);
cnt[x]+=cnt[f[x]];
return f[x]=temp;
}
bool merge(int x,int y){
int f1=find(x),f2=find(y);
if(f1==f2)return 0;
return f[f1]=f2,cnt[f1]+=s[f2],s[f2]+=s[f1],1;
}
int query(int x,int y){
return find(x)==find(y)?(abs(cnt[x]-cnt[y])-1):-1;
}
};
种类并查集
一般的并查集,维护的是具有连通性、传递性的关系,如朋友的朋友是朋友。而对于循环对称的关系,比如敌人的敌人是朋友,可以多开几个空间维护结点的敌人。
以 P1892 为例:
开两倍空间,其中结点 \(i+n\) 表示 \(i\) 的敌人,起到中转作用。
如果结点 \(A\) 与 \(B\) 为敌,则 \(A\) 与 \(B+n\),\(B\) 与 \(A+n\) 合并。
此时若 \(C\) 与 \(B\) 为敌,那么 \(A,B+n,C\) 在同一个集合中,\(A\) 与 \(C\) 就通过虚点 \(B+n\) 间接相连。
#include<bits/stdc++.h>
using namespace std;
template<unsigned int maxn>struct DSU{
int f[maxn],s[maxn];
void build(int n){
for(int i=1;i<=n;i++)s[i]=1;
}
int find(int x)
{
return f[x]?find(f[x]):x;
}
bool merge(int x,int y){
int f1=find(x),f2=find(y);
if(f1==f2)return 0;
if(s[f1]<s[f2])f[f1]=f2,s[f2]+=s[f1];
else f[f2]=f1,s[f1]+=s[f2];
return 1;
}
};
DSU<2005>a;
int n,m,ans;
int main(){
cin>>n>>m,a.build(n);
char opt;
for(int i=1,x,y;i<=m;i++){
cin>>opt>>x>>y;
if(opt=='F')a.merge(x,y);
else a.merge(x,y+n),a.merge(x+n,y);
}
for(int i=1;i<=n;i++)if(!a.f[i])ans++;
return cout<<ans<<'\n',0;
}
同理,若存在多个等价的集合,也可以用类似的方式维护。
可持久化并查集
假如把并查集用到的数组变成可持久化数组,用可持久化线段树维护,就可以存每个版本。
由于每修改一次就要创建一个新的版本,因此只能启发式合并。其中估价函数也要可持久化。
#include<bits/stdc++.h>
using namespace std;
int n,m,rt[200005];
struct node{
int f,s,ls,rs;
};
template<int maxn>struct DSU{
node tr[maxn];
int cnt;
void build(int &pos,int nl,int nr){
pos=++cnt;
if(nl==nr)tr[pos].s=1;
else{
int mid=(nl+nr)>>1;
build(tr[pos].ls,nl,mid),build(tr[pos].rs,mid+1,nr);
}
}
int query(int pos,int nl,int nr,int g){
if(nl==nr)return pos;
int mid=(nl+nr)>>1;
if(g<=mid)return query(tr[pos].ls,nl,mid,g);
else return query(tr[pos].rs,mid+1,nr,g);
}
int find(int pos,int nl,int nr,int x){
int f=tr[query(pos,nl,nr,x)].f;
return f?find(pos,nl,nr,f):x;
}
void add(int &pos,int v,int nl,int nr,int g,int k,bool f){
tr[pos=++cnt]=tr[v];
if(nl==nr){
f?tr[pos].s+=k:tr[pos].f=k;
return;
}
int mid=(nl+nr)>>1;
if(g<=mid)add(tr[pos].ls,tr[v].ls,nl,mid,g,k,f);
else add(tr[pos].rs,tr[v].rs,mid+1,nr,g,k,f);
}
bool merge(int &pos,int v,int nl,int nr,int x,int y){
int f1=find(v,nl,nr,x),f2=find(v,nl,nr,y),s1=tr[query(v,nl,nr,f1)].s,s2=tr[query(v,nl,nr,f2)].s;
if(f1==f2)return pos=v,0;
int temp=0;
if(s1<s2)add(temp,v,nl,nr,f1,f2,0),add(pos,temp,nl,nr,f2,s1,1);
else add(temp,v,nl,nr,f2,f1,0),add(pos,temp,nl,nr,f1,s2,1);
return 1;
}
};
DSU<6000005>t;
int main(){
cin>>n>>m,t.build(rt[0],1,n);
for(int i=1,opt,x,y;i<=m;i++){
cin>>opt;
if(opt==1)cin>>x>>y,t.merge(rt[i],rt[i-1],1,n,x,y);
else if(opt==2)cin>>x,rt[i]=rt[x];
else cin>>x>>y,rt[i]=rt[i-1],puts(t.find(rt[i],1,n,x)==t.find(rt[i],1,n,y)?"1":"0");
}
return 0;
}
同理,带权并查集和种类并查集也可以可持久化。
当水位线固定时,维护图中只有无积水的边的连通性,答案为 \(v\) 所在连通块中离 \(1\) 最近点到 \(1\) 的距离。可以用带权并查集维护每一个连通块的答案。先跑一遍最短路,合并时将连通块祖先的 \(dis\) 取 \(\min\)。
然而水位线是变化的,因此要把所有可能的图都建一个并查集。维护可持久化带权并查集,按 \(a\) 排序并倒着加边。询问时二分出第一个大于 \(p\) 的位置查询答案即可。
#include<bits/stdc++.h>
using namespace std;
template<typename T>void in(T &a)
{
T ans=0;
bool f=0;
char c=getchar();
for(;c<'0'||c>'9';c=getchar())if(c=='-')f=1;
for(;c>='0'&&c<='9';c=getchar())ans=ans*10+c-'0';
a=f?-ans:ans;
}
template<typename T,typename... Args>void in(T &a,Args&...args)
{
in(a),in(args...);
}
int c,n,m,dis[200005],rt[400005],,q,k,s;
vector<pair<int,int> >g[200005];
struct edge{
int u,v,l,a;
bool operator<(edge t)const{
return a<t.a;
}
}e[400005];
struct node{
int f,s,v,ls,rs;
};
template<int maxn>struct DSU{
node tr[maxn];
int cnt;
void clear(){
cnt=0,memset(tr,0,sizeof(tr));
}
void build(int &pos,int nl,int nr,int a[]){
pos=++cnt;
if(nl==nr)tr[pos].s=1,tr[pos].v=a[nl];
else{
int mid=(nl+nr)>>1;
build(tr[pos].ls,nl,mid,a),build(tr[pos].rs,mid+1,nr,a);
}
}
int query(int pos,int nl,int nr,int g){
if(nl==nr)return pos;
int mid=(nl+nr)>>1;
if(g<=mid)return query(tr[pos].ls,nl,mid,g);
else return query(tr[pos].rs,mid+1,nr,g);
}
int find(int pos,int nl,int nr,int x){
int f=tr[query(pos,nl,nr,x)].f;
return f?find(pos,nl,nr,f):x;
}
void add(int &pos,int v,int nl,int nr,int g,int k,int f){
tr[pos=++cnt]=tr[v];
if(nl==nr){
if(f==0)tr[pos].f=k;
else if(f==1)tr[pos].s+=k;
else tr[pos].v=min(tr[pos].v,k);
return;
}
int mid=(nl+nr)>>1;
if(g<=mid)add(tr[pos].ls,tr[v].ls,nl,mid,g,k,f);
else add(tr[pos].rs,tr[v].rs,mid+1,nr,g,k,f);
}
bool merge(int &pos,int v,int nl,int nr,int x,int y){
int f1=find(v,nl,nr,x),f2=find(v,nl,nr,y),p1=query(v,nl,nr,f1),p2=query(v,nl,nr,f2);
if(f1==f2)return pos=v,0;
int temp1=0,temp2=0;
if(tr[p1].s<tr[p2].s)add(temp1,v,nl,nr,f1,f2,0),add(temp2,temp1,nl,nr,f2,tr[p1].s,1),add(pos,temp2,nl,nr,f2,tr[p1].v,2);
else add(temp1,v,nl,nr,f2,f1,0),add(temp2,temp1,nl,nr,f1,tr[p2].s,1),add(pos,temp2,nl,nr,f1,tr[p2].v,2);
return 1;
}
};
DSU<20000005>t;
void dijkstra(int st,int n,vector<pair<int,int> >e[],int dis[]){
bool vis[n+5];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
for(int i=1;i<=n;i++)dis[i]=0x3f3f3f3f;
memset(vis,0,sizeof(vis)),q.push(make_pair(0,st)),dis[st]=0;
while(!q.empty()){
int now=q.top().second;
q.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=0;i<e[now].size();i++){
int v=e[now][i].first,w=e[now][i].second;
if(dis[v]>dis[now]+w)dis[v]=dis[now]+w,q.push(make_pair(dis[v],v));
}
}
}
int main(){
in(c);
while(c--){
in(n,m);
for(int i=1;i<=m;i++){
in(e[i].u,e[i].v,e[i].l,e[i].a);
g[e[i].u].push_back(make_pair(e[i].v,e[i].l)),g[e[i].v].push_back(make_pair(e[i].u,e[i].l));
}
dijkstra(1,n,g,dis),t.build(rt[m+1],1,n,dis),sort(e+1,e+m+1);
for(int i=m;i>=1;i--)t.merge(rt[i],rt[i+1],1,n,e[i].u,e[i].v);
in(q,k,s);
for(int i=1,v,p,l=0;i<=q;i++){
in(v,p),v=(v+k*l-1)%n+1,p=(p+k*l)%(s+1);
int temp=rt[upper_bound(e+1,e+m+1,edge{0,0,0,p})-e];
printf("%d\n",l=t.tr[t.query(temp,1,n,t.find(temp,1,n,v))].v);
}
memset(rt,0,sizeof(rt)),memset(e,0,sizeof(e)),t.clear();
for(int i=1;i<=n;i++)g[i].clear();
}
return 0;
}
[[数据结构]]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号