树链剖分 学习笔记
重链剖分
定义
在维护树上路径信息时,如果带修,树上倍增和树上差分无法维护。如果能把每条路径拆成若干条链,并且重新标号使链的编号连续,就可以用数据结构维护。
定义一个节点子树最大的子节点为重儿子,其余为轻儿子。节点连向重儿子的边为重边,否则为轻边。若干条重边相连为重链,单独一个节点也算重链。这样可以把整棵树分为若干条重链。
树剖过程
对树求出如下的信息:第一遍 dfs 求深度 \(dep\),父节点 \(fa\),子树大小 \(size\),重儿子 \(son\);第二遍 dfs 求所在重链深度最小的节点即链头 \(top\),新的编号 \(dfn\)。
int dep[n+5],fa[n+5],sz[n+5],son[n+5],top[n+5],dfn[n+5],cnt;
void dfs1(int pos,vector<int>e[]){
dep[pos]=dep[fa[pos]]+1,sz[pos]=1;
for(int i=0;i<e[pos].size();i++){
if(!dep[e[pos][i]]){
fa[e[pos][i]]=pos,dfs1(e[pos][i],e),sz[pos]+=sz[e[pos][i]];
if(sz[e[pos][i]]>sz[son[pos]])son[pos]=e[pos][i];
}
}
}
void dfs2(int pos,vector<int>e[]){
dfn[pos]=++cnt;
if(son[pos])top[son[pos]]=top[pos],dfs2(son[pos],e);
for(int i=0;i<e[pos].size();i++)if(!top[e[pos][i]])top[e[pos][i]]=e[pos][i],dfs2(e[pos][i],e);
}
void init(int n,int s,vector<int>e[]){
dfs1(s,e),fa[s]=top[s]=s,dfs2(s,e);
}
在搜索时先搜重儿子,使重链编号连续,这样可以使用线段树之类的数据结构维护点权。
for(int i=1;i<=n;i++)a[dfn[i]]=b[i];
维护路径
将重链作为整体,每次选择链头深度大的跳一条重链并统计答案或修改,直到路径两端在同一个重链。
void add(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]])/*[dfn[top[u]],dfn[u]]*/u=fa[top[u]];
else /*[dfn[top[v]],dfn[v]]*/v=fa[top[v]];
}
if(dep[u]>dep[v])swap(u,v);
/*[dfn[u],dfn[v]]*/
}
复杂度证明:
根据定义,一个轻儿子的父亲的子树大小不小于轻儿子的子树大小的两倍。那么跳重链时,经过轻边不超过 \(\log n\) 条,复杂度会多一只 \(\log\)。
在两个端点在同一条重链时,深度小的显然就是 lca,因此树剖可以 \(O(n)-O(\log n)\) 求 lca。
另外,交换搜索儿子的顺序,子树的编号仍然连续。因此节点 \(u\) 的子树的新标号对应区间 \([u,u+size_u-1]\)。
这样做可以维护点权。如果维护边权,可以把每条边的权放到深度大的端点上,查询和修改时需要去掉 lca 的贡献。
换根
换根只会对子树操作产生影响,不需要真正修改预处理数组。
分类讨论:
-
\(u=rt\),此时操作整棵树;
-
\(rt\) 不在 \(u\) 的子树中,操作 \(u\) 的子树;
-
\(rt\) 在 \(u\) 的子树中,比较特殊:
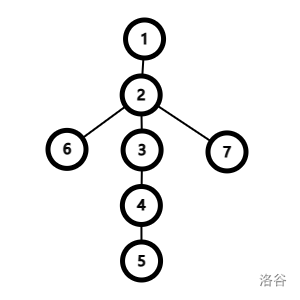
假设查询 \(2\),根是 \(4\)。
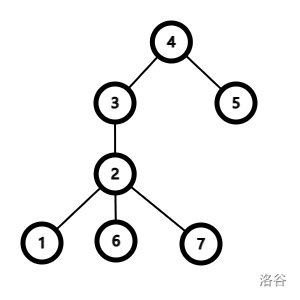
实际上修改了 \(1,2,6,7\),未修改 \(3,4,5\),发现没有修改的部分为 \(3\) 的子树。
如果 \(u\) 的儿子 \(v\) 是 \(rt\) 的祖先,那么会操作 \(v\) 的子树以外的所有节点。
找 \(v\) 时不断往上跳重链,若跳到一个链头的父节点为 \(u\),那么 \(v\) 是这个链头;否则 \(u,rt\) 在同一重链上,\(v=son_u\)。需要特判操作的区间是否为空。
void add(int u){
if(u==rt)/*[1,n]*/
else if(dfn[rt]>=dfn[u]&&dfn[rt]<dfn[u]+sz[u]){
for(int i=rt;top[i]!=top[u];i=fa[top[i]]){
if(fa[top[i]]==u){
/*[1,dfn[top[i]]-1],[dfn[top[i]]+sz[top[i]],n]*/
return;
}
}
/*[1,dfn[son[u]]-1],[son[u]]+sz[son[u]],n]*/
}
else /*[dfn[u],dfn[u]+sz[u]-1]*/
}
长链剖分
定义
定义重儿子为子树深度最大的子节点,其余定义与重链剖分一样。
重要性质:一个节点的 \(k\) 级祖先所在的重链长不小于 \(k\)。因为这个祖先到这个点就经过了 \(k\) 条边,根据定义,最大深度不会小于 \(k\)。
树上 k 级祖先
一棵树,多次询问节点 \(x\) 的第 \(k\) 级祖先。
树上倍增 \(O(n\log n)-O(\log n)\),重链剖分可以 \(O(n)-O(\log n)\)。但是长链剖分可以做到 \(O(n\log n)-O(1)\)。
设 \(2^i\leq k\leq 2^{i+1}\),首先跳到 \(x\) 的 \(2^i\) 级祖先,这个节点与 \(k\) 级祖先的距离小于 \(2^i\)。根据性质,这个点所在的重链长 \(len\geq2^i\)。因此跳到链头后往上或往下找至多 \(len\) 个节点就是答案。
预处理每个节点的 \(2\) 次幂级祖先和每个链头的 \(len\) 级儿子与祖先即可 \(O(1)\) 回答。
int lg[n+5],dep[n+5],maxd[n+5],f[n+5][log2(n)+5],son[n+5],top[n+5];
vector<int>up[n+5],down[n+5];
void dfs1(int pos,vector<int>e[]){
maxd[pos]=dep[pos]=dep[f[pos][0]]+1;
for(int i=1;i<=lg[dep[pos]]+1;i++)f[pos][i]=f[f[pos][i-1]][i-1];
for(int i=0;i<e[pos].size();i++){
if(!dep[e[pos][i]]){
f[e[pos][i]][0]=pos,dfs1(e[pos][i],e);
if(maxd[e[pos][i]]>maxd[pos])maxd[pos]=maxd[e[pos][i]],son[pos]=e[pos][i];
}
}
}
void dfs2(int pos,vector<int>e[]){
if(son[pos])top[son[pos]]=top[pos],dfs2(son[pos],e);
for(int i=0;i<e[pos].size();i++)if(!top[e[pos][i]])top[e[pos][i]]=e[pos][i],dfs2(e[pos][i],e);
if(top[pos]==pos){
for(int i=0,t=pos;i<=maxd[pos]-dep[pos];i++)up[pos].push_back(t),t=f[t][0];
for(int i=0,t=pos;i<=maxd[pos]-dep[pos];i++)down[pos].push_back(t),t=son[t];
}
}
void init(int n,int s,vector<int>e[]){
for(int i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
dfs1(s,e),top[s]=s,dfs2(s,e);
}
int la(int x,int k){
if(!k)return x;
x=f[x][lg[k]],k-=(1<<lg[k])+(dep[x]-dep[top[x]]),x=top[x];
return k>=0?up[x][k]:down[x][-k];
}
长链剖分优化DP
长链剖分可以快速合并子树以深度为下标的信息。
设 \(f_{u,dep}\) 表示 \(u\) 的子树中到 \(u\) 距离为 \(dep\) 的个数。显然 \(f_{u,dep}=\sum_{v\in son_u}f_{v,dep-1}\)。
不能直接暴力合并子树,但是第一个合并的子节点可以直接用指针 \(O(1)\) 复制。
对树长剖,先搜重儿子,重儿子的 \(f\) 指针直接指向当前节点的指针加一,这样就实现了 \(O(1)\) 拷贝。由于长剖的性质,只用对每个链头开链长的内存,空间是 \(O(n)\) 的。而重剖就不能保证。
每条重链会被暴力合并一次,时间复杂度 \(O(n)\)。
显然 \(b\) 和 \(a\) 应该是祖先和儿子的关系。若 \(b\) 是 \(a\) 的祖先,答案为 \(\min(dep_p-1,k)\times size_p\)。
用 DP 统计 \(a\) 是 \(b\) 的祖先的情况,设 \(f_{u,dep}\) 表示答案,有 \(f_{u,dep}=\sum_{v\in son_u}f_{v,dep-1}+size_v-1\)。
这就很像上面的题,由于加了一个数,不能直接合并。打一个标记表示整体加的常数,由于 \(f_{u,0}\) 不受影响,需要减去标记。
#include<bits/stdc++.h>
using namespace std;
int n,m,sz[300005],dep[300005],len[300005],son[300005];
long long temp[300005],v[300005],*f[300005],*now=temp,ans[300005];
vector<int>e[300005];
vector<pair<int,int>>q[300005];
void dfs1(int pos,int fa){
dep[pos]=dep[fa]+1,sz[pos]=1;
for(int i=0;i<e[pos].size();i++){
if(e[pos][i]!=fa){
dfs1(e[pos][i],pos),sz[pos]+=sz[e[pos][i]];
if(len[e[pos][i]]>len[son[pos]])son[pos]=e[pos][i];
}
}
len[pos]=len[son[pos]]+1;
}
void dfs2(int pos,int fa){
if(son[pos])f[son[pos]]=f[pos]+1,dfs2(son[pos],pos),f[pos][0]=0,v[pos]+=v[son[pos]]+sz[son[pos]]-1;
for(int i=0;i<e[pos].size();i++){
if(e[pos][i]==fa||e[pos][i]==son[pos])continue;
f[e[pos][i]]=now,now+=len[e[pos][i]],dfs2(e[pos][i],pos),v[pos]+=v[e[pos][i]]+sz[e[pos][i]]-1;
for(int j=1;j<=len[e[pos][i]];j++)f[pos][j]+=f[e[pos][i]][j-1];
}
f[pos][0]=-v[pos];
for(int i=0;i<q[pos].size();i++)ans[q[pos][i].second]=f[pos][min(q[pos][i].first,len[pos]-1)]+v[pos];
}
int main(){
cin>>n>>m;
for(int i=1,u,v;i<n;i++)cin>>u>>v,e[u].push_back(v),e[v].push_back(u);
for(int i=1,u,v;i<=m;i++)cin>>u>>v,q[u].push_back(make_pair(v,i));
dfs1(1,0),f[1]=now,now+=len[1],dfs2(1,0);
for(int i=1;i<=n;i++)for(int j=0;j<q[i].size();j++)ans[q[i][j].second]+=1ll*min(q[i][j].first,dep[i]-1)*(sz[i]-1);
for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';
return 0;
}
[[树论]]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号