笛卡尔树 学习笔记

概述

笛卡尔树是一种特殊的二叉树，每个节点有两个值 \(x,y\)，\(x\) 满足二叉查找树的性质，\(y\) 满足堆的性质。即 \(x_{lson(u)}<x_u<x_{rson{u}}\)，\(y\) 根据堆的种类有 \(x_{lson(u)}<x_u\wedge x_{rson(u)}<x_u\) 或 \(x_{lson(u)}>x_u\wedge x_{rson(u)}>x_u\)。

当节点的两种值各自互不相同时，笛卡尔树唯一。

建树

P5854模板

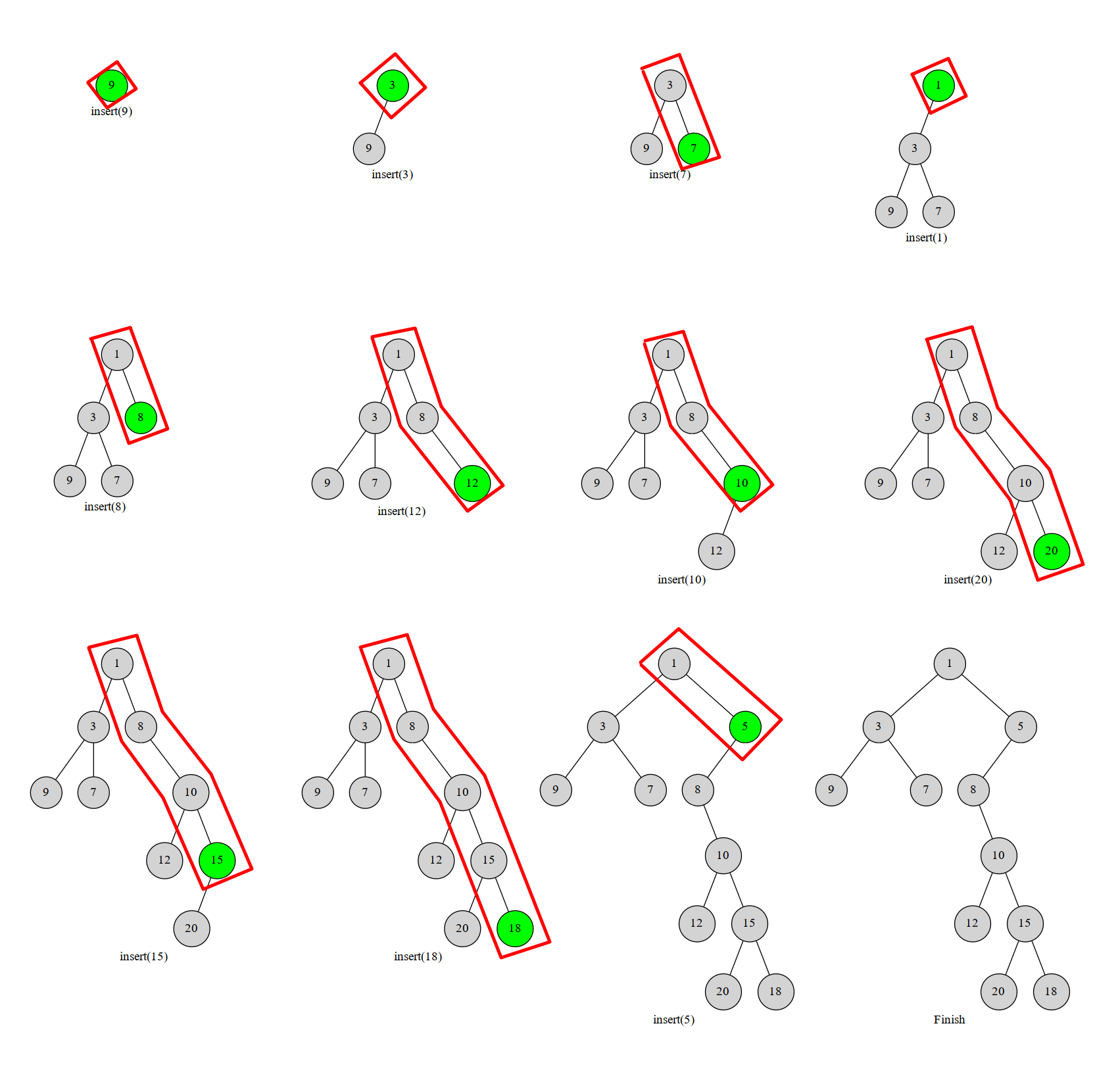
首先按 \(x\) 排序。板子题中是一种特殊的笛卡尔树，\(x\) 为编号，\(y\) 为点权，省掉了排序的过程。

新插入的节点满足 \(x\) 最大，那么这个节点一定落在右链的末尾。维护一个栈表示右链。自底向上找到右链上第一个满足 \(y\) 的性质可以插入的位置，把新点接到右儿子上。那么原来的右子树就接到新点的左子树上以保持 \(x\) 的性质。

搬一张 OI-wiki 的图：

struct node{
  int ls,rs;
}tr[n+5];
int st[n+5],top;
int build(int n,int a[]){
  for(int i=1,pos;i<=n;i++){
    pos=top;
    while(pos&&a[st[pos]]>a[i])pos--;
    if(pos)tr[st[pos]].rs=i;
    if(pos<top)tr[i].ls=st[pos+1];
    st[++pos]=i,top=pos;
  }
  return st[1];
}

例题

P1377

这一题中，节点的权值满足二叉查找树的性质。而由于插入编号递增，隐含了编号满足堆的关系。

那么这是一棵笛卡尔树，\(x\) 为点权，\(y\) 为编号。建树后输出先序遍历即可。

#include<bits/stdc++.h>
using namespace std;
struct node{
  int ls,rs;
}tr[100005];
int st[100005],top;
int build(int n,int a[]){
  for(int i=1,pos;i<=n;i++){
    pos=top;
    while(pos&&a[st[pos]]>a[i])pos--;
    if(pos)tr[st[pos]].rs=i;
    if(pos<top)tr[i].ls=st[pos+1];
    st[++pos]=i,top=pos;
  }
  return st[1];
}
void out(int pos)
{
  if(pos)cout<<pos<<' ',out(tr[pos].ls),out(tr[pos].rs);
}
int n,a[100005];
int main(){
  cin>>n; 
  for(int i=1,temp;i<=n;i++)cin>>temp,a[temp]=i;
  return out(build(n,a)),0;
}

P6453

笛卡尔树+树形dp。

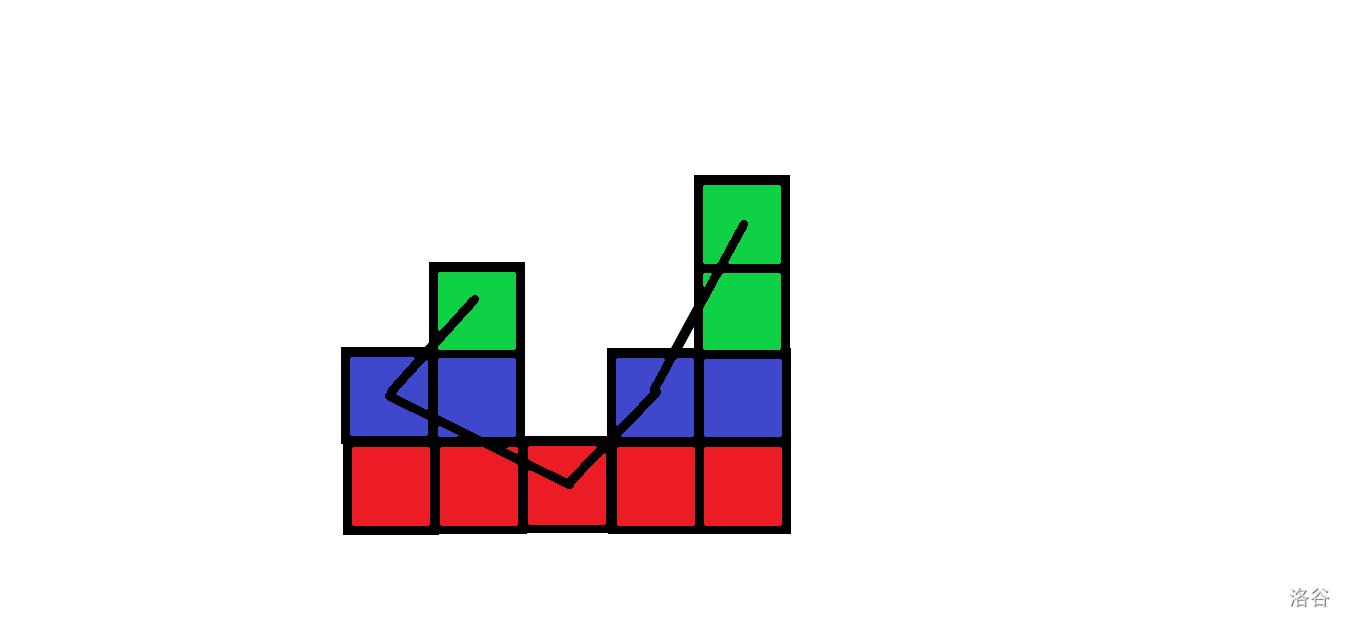
如图，对图形自底向上划分成若干个矩形，发现这些矩形形成一个树形的结构，而且满足祖先的 \(h\) 更小。那么可以以 \(x\) 为编号，\(y\) 为 \(h\) 建立小根笛卡尔树，其中节点 \(u\) 的长为 \(size_u\)，宽为 \(h_u-h_{fa_u}\)。这样划分后兄弟节点是独立的，可以树形 DP。

设 \(f_{i,j}\) 表示节点 \(i\) 的子树中选 \(j\) 个的方案数，类似树上背包用乘法原理合并即可。

这一题中没有依赖关系，因此对节点本身需要单独合并。若当前矩形选了 \(k\) 个，则当前矩形的方案为 \(C_{size_i-(j-k)}^kC_{h_u-h_{fa_u}}^kk!\)。

#include<bits/stdc++.h>
using namespace std;
const long long mod=1000000007;
int n,m,st[505],top,h[505],rt,s[505];
long long f[505][505],fac[1000005],vac[1000005];
struct node{
  int ls,rs;
}tr[505];
template<typename T>T qpow(T a,T b,T n,T ans=1){
  for(a%=n;b;b>>=1)b&1&&(ans=1ll*ans*a%n),a=1ll*a*a%n;
  return ans;
}
template<typename T>T inv(T a,T b)
{
  return qpow(a,b-2,b);
}
template<typename T>void inv_fac(int n,T p,T fac[],T vac[]){
  fac[0]=1;
  for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%p;
  vac[0]=1,vac[n]=inv(fac[n],p);
  for(int i=n-1;i>=1;i--)vac[i]=vac[i+1]*(i+1)%p;
}
int build(int n,int a[]){
  for(int i=1;i<=n;i++){
    while(top&&a[st[top]]>a[i])tr[i].ls=st[top--];
    if(top)tr[st[top]].rs=i;
    st[++top]=i;
  }
  return st[1];
}
long long C(int n,int m){
  return fac[n]*vac[m]%mod*vac[n-m]%mod;
}
void dfs(int pos,int fa){
  f[pos][0]=s[pos]=1;
  if(tr[pos].ls){
    dfs(tr[pos].ls,pos),s[pos]+=s[tr[pos].ls];
    for(int i=min(s[pos],m);i>=1;i--)for(int j=1;j<=min(s[tr[pos].ls],i);j++)f[pos][i]=(f[pos][i]+f[tr[pos].ls][j]*f[pos][i-j]%mod)%mod;
  }
  if(tr[pos].rs){
    dfs(tr[pos].rs,pos),s[pos]+=s[tr[pos].rs];
    for(int i=min(s[pos],m);i>=1;i--)for(int j=1;j<=min(s[tr[pos].rs],i);j++)f[pos][i]=(f[pos][i]+f[tr[pos].rs][j]*f[pos][i-j]%mod)%mod;
  }
  for(int i=min(s[pos],m);i>=1;i--)for(int j=1;j<=min(h[pos]-h[fa],i);j++)f[pos][i]=(f[pos][i]+fac[j]*f[pos][i-j]%mod*C(h[pos]-h[fa],j)%mod*C(s[pos]-i+j,j)%mod)%mod;
}
int main(){
  cin>>n>>m,inv_fac(1000000,mod,fac,vac);
  for(int i=1;i<=n;i++)cin>>h[i];
  return rt=build(n,h),dfs(rt,0),cout<<f[rt][m]<<'\n',0;
}

CF1580D

建出笛卡尔树，在笛卡尔树上 DP。

设 \(f_{pos,k}\) 为在节点 \(pos\) 的子树里选 \(k\) 个的最大值，枚举左右子树分别选了 \(i,j\) 个。由于 \(pos\) 是子树所代表的区间中最小的，因此每个跨越 \(pos\) 的区间的 \(f\) 都为 \(a_{pos}\)。则有 \(f_{ls,i}+f_{rs,j}-2ija_{pos}\to f_{pos,i+j},f_{ls,i}+f_{rs,j}-(2ij+2i+2j)a_{pos}\)。

#include<bits/stdc++.h>
using namespace std;
int n,m,rt,st[4005],s[4005],top;
long long a[4005],f[4005][4005];
struct node{
  int ls,rs;
}tr[4005];
int build(int n,long long a[]){
  for(int i=1,pos;i<=n;i++){
    pos=top;
    while(pos&&a[st[pos]]>a[i])pos--;
    if(pos)tr[st[pos]].rs=i;
    if(pos<top)tr[i].ls=st[pos+1];
    st[++pos]=i,top=pos;
  }
  return st[1];
}
void dfs(int pos){
  s[pos]=1;
  if(tr[pos].ls)dfs(tr[pos].ls),s[pos]+=s[tr[pos].ls];
  if(tr[pos].rs)dfs(tr[pos].rs),s[pos]+=s[tr[pos].rs];
  for(int i=0;i<=s[tr[pos].ls];i++){
    for(int j=0;j<=s[tr[pos].rs];j++){
      f[pos][i+j]=max(f[pos][i+j],f[tr[pos].ls][i]+f[tr[pos].rs][j]-2ll*i*j*a[pos]);
      f[pos][i+j+1]=max(f[pos][i+j+1],f[tr[pos].ls][i]+f[tr[pos].rs][j]+m*a[pos]-(2ll*(i+1)*(j+1)-1)*a[pos]);
    }
  }
}
int main(){
  memset(f,-0x3f,sizeof(f)),f[0][0]=0,cin>>n>>m;
  for(int i=1;i<=n;i++)cin>>a[i];
  return rt=build(n,a),dfs(rt),cout<<f[rt][m]<<'\n',0;
}

进一步地，可以不建出树，而是按最小值分治。

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a[4005];
vector<long long>solve(int l,int r){
  vector<long long>f(r-l+2,-0x3f3f3f3f3f3f3f3f);
  f[0]=0;
  if(l>r)return f;
  int pos=l;
  for(int i=l;i<=r;i++)if(a[i]<a[pos])pos=i;
  vector<long long>fl=solve(l,pos-1),fr=solve(pos+1,r);
  for(int i=0;i<fl.size();i++){
    for(int j=0;j<fr.size();j++){
      f[i+j]=max(f[i+j],fl[i]+fr[j]-2ll*i*j*a[pos]);
      f[i+j+1]=max(f[i+j+1],fl[i]+fr[j]+m*a[pos]-(2ll*(i+1)*(j+1)-1)*a[pos]);
    }
  }
  return f;
}
int main(){
  cin>>n>>m;
  for(int i=1;i<=n;i++)cin>>a[i];
  return cout<<solve(1,n)[m]<<'\n',0;
}

[[树论]]