树形DP 学习笔记

树形DP

树形DP，就是在树上DP，一般会在DFS中进行。

例题：P1352

一般遇到考树的题目，先想链上的做法，然后推广到树。链上的问题是这样的：

\(n\) 个职员，选择若干个参加宴会，相邻的不能同时参加，问快乐指数之和的最大值。

设 \(f_{i,j}\)，其中 \(j\) 是布尔值，表示前 \(i\) 个人，第 \(i\) 个人参加或不参加的最大值。显然 \(f_{i,0}=\max(f_{i-1,0},f_{i-1,1}),f_{i,1}=f_{i-1,0}\)，初始化 \(f_{i,0}=0,f_{i,1}=r_i\)，答案 \(\max(f_{n,0},f_{n,1})\)。

转换到树上，就变成 \(i\) 的子树，第 \(i\) 个人参加或不参加的最大值。转移方程 \(f_{i,0}=\sum_{x\in son_i}\max(f_{x,0},f_{x,1}),f_{i,1}=\sum_{x\in son_i}f_{i-1,0}\)。

#include<bits/stdc++.h>
using namespace std;
int n,r[6005],f[6005][2];
vector<int>e[6005];
bool vis[6005];
void dfs(int pos,int fa){
  f[pos][1]=r[pos];
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs(e[pos][i],pos),f[pos][1]+=f[e[pos][i]][0],f[pos][0]+=max(f[e[pos][i]][0],f[e[pos][i]][1]);
}
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>r[i];
  for(int i=1,u,v;i<n;i++)cin>>u>>v,e[u].push_back(v),e[v].push_back(u),vis[v]=1;
  for(int i=1;i<=n;i++)if(!vis[i])return dfs(i,0),cout<<max(f[i][0],f[i][1])<<'\n',0;
  return 0;
}

换根DP

换根DP是树形DP的一种，不过相较其他树形DP的做法更特别，需要DFS两次。

例题：P3478

暴力的做法是对于每个点DFS，这样显然会TLE。时间复杂度只能承受求一个点的答案，设这个点为 \(1\) 号。

换根DP的主要思想是用这一个节点的答案快速推出其他答案。假设这棵树是这样的：

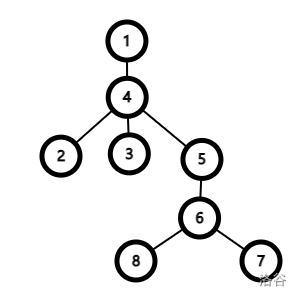
将 \(1\) 的子节点作为根，树变成了这样：

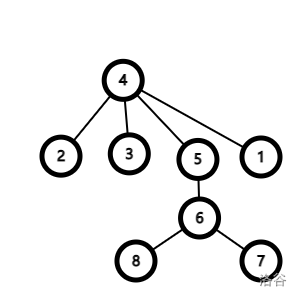
\(4\) 的子树的深度减少了一，其他节点增加了一。

可以得到递推式：设 \(u\) 是 \(v\) 的父节点，\(size\) 表示子树大小，\(f_v=f_u-size_v+(n-size_v)=f_u+n-2size_v\)。

那么进行第二次DFS转移即可。

#include<bits/stdc++.h>
using namespace std;
int n,ans;
long long f[1000005],maxn,d[1000005],s[1000005];
vector<int>e[1000005];
void dfs1(int pos,int fa){
  s[pos]=1,d[pos]=d[fa]+1;
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs1(e[pos][i],pos),s[pos]+=s[e[pos][i]];
}
void dfs2(int pos,int fa){
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)f[e[pos][i]]=f[pos]+n-s[e[pos][i]]*2,dfs2(e[pos][i],pos);
}
int main(){
  cin>>n;
  for(int i=1,u,v;i<n;i++)cin>>u>>v,e[u].push_back(v),e[v].push_back(u);
  dfs1(1,0);
  for(int i=1;i<=n;i++)f[1]+=d[i];
  dfs2(1,0);
  for(int i=1;i<=n;i++)if(f[i]>maxn)maxn=f[i],ans=i;
  return cout<<ans<<'\n',0;
}

树上背包

树上背包就是在树上的背包问题，物品会有前置条件的限制。比如选了物品 \(u\)，必须选物品 \(v\)，这些关系形成一棵树。需要在这棵树上选出一个包含根的连通块，在满足其他限制时价值最大。

P2014

把 \(0\) 号看作一个节点，价值为 \(0\)，就保证了图联通。这样变成一个比较简单的树上 0/1 背包模型。每个物品的重量 \(1\)，背包容量 \(m\)。

设 \(f_{u,i,j}\) 表示节点 \(u\) 的子树中，节点 \(u\) 与前 \(i\) 个子树选 \(j\) 个的最大价值。那么转移方程 \(f_{u,i,j}=\max_{v\in son(u)}(f_{u,i-1,j-k}+f_{v,size(v),k})(0\leq k<j)\)，表示将前 \(i-1\) 棵子树的答案与第 \(i\) 棵合并 。用三重循环转移，分别枚举子节点，选的个数，子节点的子树中选的个数。

这个式子显然可以压掉 \(i\) 一维。类比普通 0/1 背包，选的个数应该倒序枚举。

#include<bits/stdc++.h>
using namespace std;
int n,m,v[305],f[305][305];
vector<int>e[305];
void dfs(int pos,int fa){
  f[pos][1]=v[pos];
  for(int i=0;i<e[pos].size();i++){
    if(e[pos][i]==fa)continue;
    dfs(e[pos][i],pos);
    for(int j=m+1;j>=1;j--)for(int k=0;k<j;k++)f[pos][j]=max(f[pos][j],f[e[pos][i]][k]+f[pos][j-k]);
  }
}
int main(){
  cin>>n>>m;
  for(int i=1,t;i<=n;i++)cin>>t>>v[i],e[t].push_back(i),e[i].push_back(t);
  return dfs(0,-1),cout<<f[0][m+1]<<'\n',0;
}

时间复杂度 \(O(n^2m)\)。

可以优化，对于内层，可以去掉一些多余的循环。

记录一下子树大小 \(size\)，并在循环中更新。这样没有更新完的 \(size\) 就表示子节点子树大小的前缀和。

显然在前 \(i-1\) 棵子树中最多只能选 \(size_u\) 个，第 \(i\) 棵子树最多选 \(size_v\) 个。注意此时 \(size_u\) 没有更新完，而 \(size_v\) 更新完。

void dfs(int pos,int fa){
  f[pos][1]=v[pos],s[pos]=1;
  for(int i=0;i<e[pos].size();i++){
    if(e[pos][i]==fa)continue;
    dfs(e[pos][i],pos),s[pos]+=s[e[pos][i]];
    for(int j=min(m+1,s[pos]);j>=1;j--)for(int k=0;k<=min(j-1,s[e[pos][i]]);k++)f[pos][j]=max(f[pos][j],f[e[pos][i]][k]+f[pos][j-k]);
  }
}

复杂度证明较为复杂，是 \(O(nm)\) 的。

[[动态规划]]