动态规划-----编辑距离

　　编辑距离，计算从一个字符串到另一个字符串的最短编辑距离，其可以通过增、删、替方式来实现。

　　例如:字符串str1 = mitcmu，与字符串str2=mtacnu，字符串str1通过增、删、替方式变成str2，最短编辑距离为3：

　　第一步：str1删除字符i，变成str1=mtcmu；

　　第二步：str1在字符t后面增加字符a，变成str1=mtacmu；

　　第三步：str1中的字符m替换成n，变成str1=mtacnu = str2。

　　编辑距离，分为莱文斯坦距离与最长公共子串长度，两者区别：莱文斯坦距离，从一个字符串实现成为另一个字符串的最少编辑距离，操作方式有增、删、替方式；最长公共子串长度，则计算两个字符串之间的相同字符串长度，操作方式有增、删。

1. 莱文斯坦距离

　　解题思路，回溯法：

　　(1).匹配str1[i]和str2[j]

　　a.匹配：

　　  匹配str1[i+1]和str2[j+1]

　　b.不匹配：

　　  1).可以删除str1[i]，然后递归考察str1[i+1]和str2[j]

　　  2).可以删除str2[j]，然后递归考察str1[i]和str2[j+1]

　　  3).可以在str1[i]前面添加一个跟str2[j]相同字符，让递归考察str1[i]和str2[j+1]

　　  4).可以在str2[j]前面添加一个跟str1[i]相同字符，让递归考察str1[i+1]和str2[j]

　　  5).可以将str1[i]替换成str2[j]，或者将str2[j]替换成str1[i]，然后递归考察str1[i+1]和str2[j+1]

　　决策图用函数f(i,j,dis)表示树，其中i表示第一个字符串里面的字符，j表示第二个字符串的zif，dis表示距离：

 

 

 

 

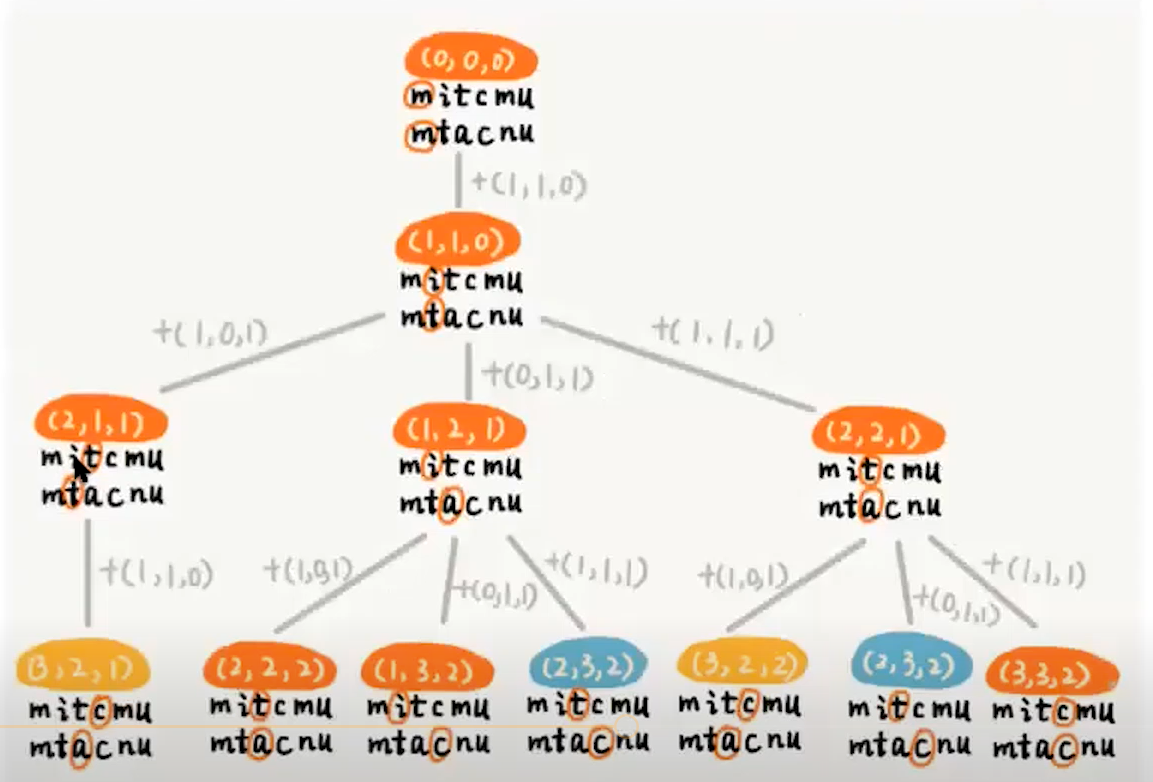
　　由图可以得出：编辑距离通过增、删、替方式来获取每个步骤的最短距离，由此可以获取如下规律

 

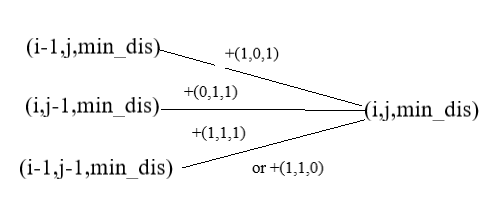
 　　从中我们可以得出状态转移方程：

　　(1)如果str1[i] != str2[j]，那么达到每一个步骤的最短距离

　　min_dis(i,j) = min(min_dis(i-1,j)+1,min_dis(i,j-1)+1,min_dis(i-1,j-1)+1)

 

　　(2)如果str1[i] == str2[j], 那么达到每一个步骤的最短距离

       min_dis(i,j) = min(min_dis(i-1,j),min_dis(i,j-1),min_dis(i-1,j-1))

　　由上，可得出动态规划法：

　　(1)初始化表格

　　

	""	m	t	a	c	n	u
""	0	1	2	3	4	5	6
m	1
i	2
t	3
c	4
m	5
u	6

　　(2)第一行计算：根据回溯法，j计算m变成m,mt，mta,mtac,mtacn,mtacnu所需要的距离

　　

	""	m	t	a	c	n	u
""	0	1	2	3	4	5	6
m	1	0	1	2	3	4	5
i	2
t	3
c	4
m	5
u	6

 

　　(3)第二行计算：根据回溯法，j计算mi变成m,mt，mta,mtac,mtacn,mtacnu所需要的距离

 

	""	m	t	a	c	n	u
""	0	1	2	3	4	5	6
m	1	0	1	2	3	4	5
i	2	1	1	2	3	4	5
t	3
c	4
m	5
u	6

 

　　(6)依此类推第六行计算：根据回溯法，j计算m变成m,mt，mta,mtac,mtacn,mtacnu所需要的距离

 

	""	m	t	a	c	n	u
""	0	1	2	3	4	5	6
m	1	0	1	2	3	4	5
i	2	1	1	2	3	4	5
t	3	2	1	2	3	4	5
c	4	3	2	2	2	3	4
m	5	3	3	3	3	3	4
u	6	4	4	4	4	4	3

 

　　因此代码实现如下

　　

import numpy as np


#编辑距离之莱温斯坦距离，用于计算两个字符串之间的相似度

def LewinsteinDistance(strFirst,strSecond):
    #用于储存每一步的最短距离的值
    editDis = np.zeros(shape=(len(strFirst) + 1, len(strSecond) + 1))
    for i in range(len(editDis)):
        for j in range(len(editDis[i])):
            #初始化i==0,即行为0时的值，为0，1，2......
            if i == 0:
                editDis[i][j] = j
            # 初始化j==0,即列为0时的值，为0，1，2......
            elif j == 0:
                editDis[i][j] = i
            else:
                #两个字符不匹配
                if strFirst[i-1] != strSecond[j-1]:
                    editDis[i][j] = min(editDis[i-1][j-1]+1,editDis[i-1][j]+1, editDis[i][j-1]+1)
                else:
                    # 两个字符匹配
                    editDis[i][j] = min(editDis[i - 1][j - 1] , editDis[i - 1][j] , editDis[i][j - 1] )

    for i in range(len(editDis)):
        for j in range(len(editDis[j])):
            print(editDis[i][j], end="    ")
        print()
strSecond= "mtacnu"
strFirst = "mitcmu"

#strSecond= "flaw"
#strFirst = "lawn"
LewinsteinDistance(strFirst,strSecond)

 

结果输出：

0.0    1.0    2.0    3.0    4.0    5.0    6.0    
1.0    0.0    1.0    2.0    3.0    4.0    5.0    
2.0    1.0    1.0    2.0    3.0    4.0    5.0    
3.0    2.0    1.0    2.0    3.0    4.0    5.0    
4.0    3.0    2.0    2.0    2.0    3.0    4.0    
5.0    3.0    3.0    3.0    3.0    3.0    4.0    
6.0    4.0    4.0    4.0    4.0    4.0    3.0    

　　　2.最长公共子串长度

　　　状态转移方程：

　　　(1)　str1[i]==str2[j]:

　　　　max_Long(i,j)=max(max_Long(i-1,j-1)+1,max_Long(i-1,j),max_Long(i,j-1))

　　　(2) str1[i] != str2[j]

　　　　max_long(i,j)=max(max_Long(i-1,j-1),max_Long(i-1,j),max_Long(i,j-1))

　　算法实现：

　　

import numpy as np
#最长公共子串
def LongestCommonCubstring(strFirst,strSecond):
    editDis = np.zeros(shape=(len(strFirst) + 1, len(strSecond) + 1))
    for i in range(1,len(editDis)):
        for j in range(1,len(editDis[i])):

            if strFirst[i - 1] != strSecond[j - 1]:
                editDis[i][j] = max(editDis[i - 1][j - 1] , editDis[i - 1][j] , editDis[i][j - 1] )
            else:
                editDis[i][j] = max(editDis[i - 1][j - 1] + 1, editDis[i - 1][j], editDis[i][j - 1])

    for i in range(len(editDis)):
        for j in range(len(editDis[j])):
            print(editDis[i][j], end="    ")
        print()
strSecond= "mtacnu"
strFirst = "mitcmu"
LongestCommonCubstring(strFirst,strSecond)

 

输出

0.0    0.0    0.0    0.0    0.0    0.0    0.0    
0.0    1.0    1.0    1.0    1.0    1.0    1.0    
0.0    1.0    1.0    1.0    1.0    1.0    1.0    
0.0    1.0    2.0    2.0    2.0    2.0    2.0    
0.0    1.0    2.0    2.0    3.0    3.0    3.0    
0.0    1.0    2.0    2.0    3.0    3.0    3.0    
0.0    1.0    2.0    2.0    3.0    3.0    4.0