动态规划------背包问题
一、背包问题之最大容量
1.问题描述:
假设背包能装9kg的东西,现在有五个物品分别是2,2,4,6,3kg,在不超过背包容量的范围内,能装的最大容量是多少呢?
解法一:回溯法,即决策树。
方法描述:从第一个物品到最后一个物品开始,做出决策,即装或不装,使用函数f(x,y)表示,其中x表示第X个物品,y表示第X个物品被装或者没有被装后的物品总质量。最后形成的决策树如下图所示,左节点表示当前物品没有被不装,右节点表示当前物品被装。
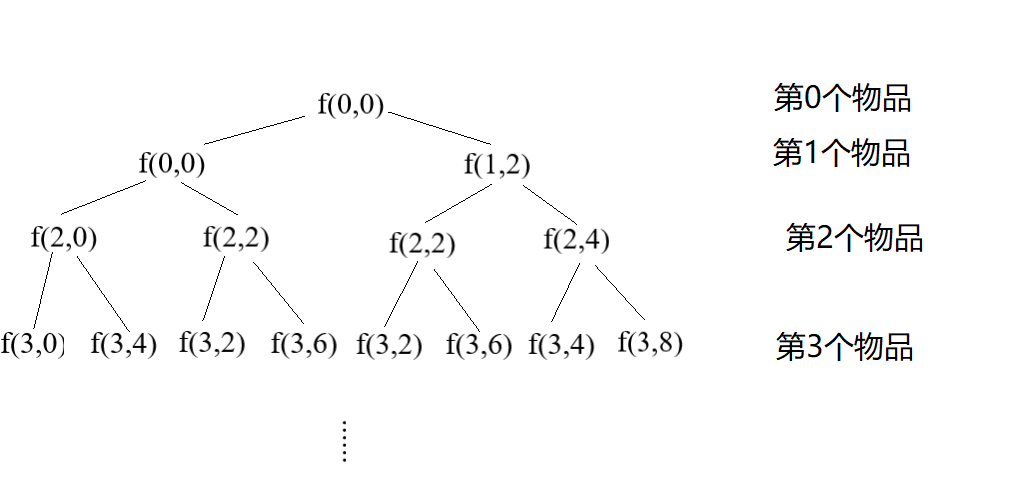
方法二:动态规划
方法描述:将重量与物品数量装换成矩阵,如下表所示
初始状态:列表示物品编号,行表示总重量,用1所处位置表示当表当前物品被装或不装的总量
| 0kg | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg | 7kg | 8kg | 9kg | |
| 0(2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1(2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2(4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3(6) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4(3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
第一个物品状态:
| 0kg | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg | 7kg | 8kg | 9kg | |
| 0(2) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1(2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2(4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3(6) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4(3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
如表所示,第一个物品不装和被装下的总量分别为0Kg,2kg(标1处)
第二个物品状态:
| 0kg | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg | 7kg | 8kg | 9kg | |
| 0(2) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1(2) | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2(4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3(6) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4(3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
如上表所示,第二个物品在第一个物品做出决策后,继续做出决策(装/不装),总量分别为0,2,4kg,依此类推,到第五个物品做出决策后表如下所示
| 0kg | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg | 7kg | 8kg | 9kg | |
| 0(2) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1(2) | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2(4) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3(6) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4(3) | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
因此动态算法之背包问题代码如下所示
1 import numpy as np 2 #背包基础版本容量最大 3 def maxWeight(backp,backValues): 4 for j in range(len(backp)): 5 #第一个物品装或不装的状态1 6 if j == 0: 7 #不装 8 backp[j][0]=1 9 #装 10 backp[j][2] = 1 11 else: 12 for i in range(len(backp[j])): 13 #查询在上一个条件下(装或不装的物品) 14 if backp[j-1][i]==1: 15 #不装物品 16 backp[j][i] = 1 17 #判断上一个物品(装或不装的物品状态)即用下标(重量)与当前物品重量之和是否超过总重量,不超过,标记为1 18 if i+backValues[j]<len(backp[j]): 19 backp[j][i+backValues[j]] = 1 20 21 22 23 for j in range(len(backp)): 24 25 for i in range(len(backp[j])): 26 27 #if backp[j][i] = 1 28 print(backp[j][i],end=" ") 29 print() 30 backp = np.zeros(shape=(5,10))#二维数组5代表物品编号,10代表给定的要装的总重量 31 print(len(backp)) 32 backValues = [2,2,4,6,3] 33 maxWeight(backp,backValues)
结果如下所示:
1.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
二、背包问题之最大价值
问题描述:给定五个物品,其重量分别是3、2、1、1、4,其价值分别是5、2、4、2、10,假设有个背包总容量为8,在不超过背包总容量的情况下,其能装的最大价值是多少?
解题思路:本题中,出现了3个变量,分别是重量,容量,价值,我们用函数f(x,y,z)来表示
方法1:回溯法即决策树,如下图所示:
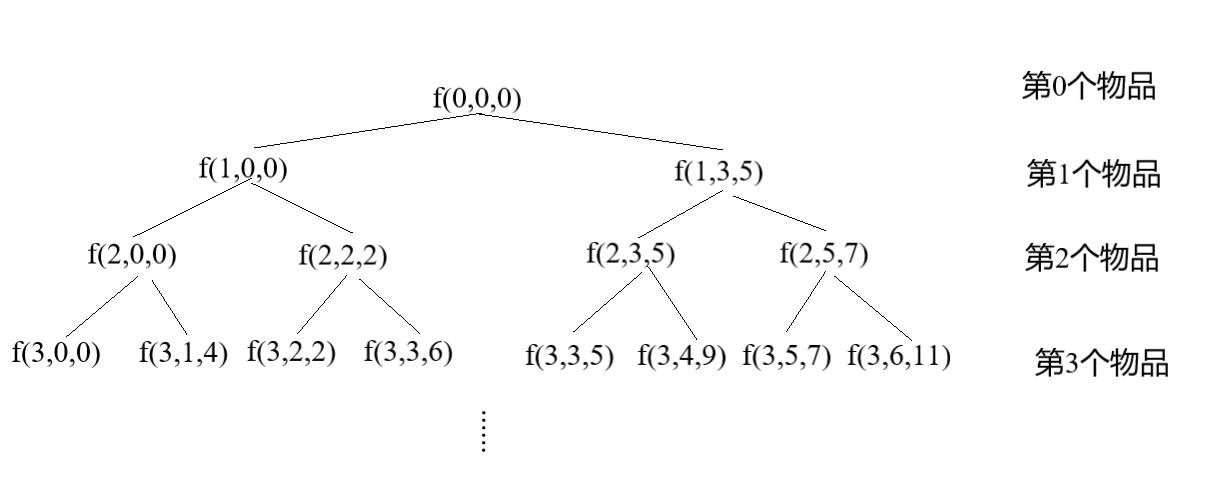
方法2:动态规划如下表所示
| 0kg | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg | 7kg | 8kg | |
| 0(3) | 0 | -1 | -1 | 5 | -1 | -1 | -1 | -1 | -1 |
| 1(2) | 0 | -1 | 2 | 5 | -1 | 7 | -1 | -1 | -1 |
| 2(1) | 0 | 4 | 2 | 6 | 9 | 7 | 11 | -1 | -1 |
| 3(1) | 0 | 4 | 6 | 6 | 9 | 11 | 11 | 13 | -1 |
| 4(4) | 0 | 4 | 6 | 6 | 10 | 14 | 16 | 16 | 19 |
因此动态算法之背包问题代码如下所示
1 import numpy as np 2 #背包升级版本,加入价值体系 3 #backValues[j][0]为物品重量,backValues[j][1]物品价值 4 def maxWeightValues(backp,backValues): 5 goodsValues =np.zeros(shape=[len(backp[0])])#用于记录当前重量的最大价值 6 for j in range(len(backp)): 7 #第一个物品装或不装的状态1 8 if j == 0: 9 #不装 10 backp[j][0]=0 11 #装 12 backp[j][backValues[j][0]] = backValues[j][1] 13 goodsValues[backValues[j][0]] = backValues[j][1] 14 else: 15 for i in range(len(backp[j])): 16 #查询在上一个条件下(装或不装的物品) 17 if backp[j-1][i] >=0 : 18 #不装物品,判断当前总重量的价值和与上一个物品状态下(截止到当前被操作物品总重量的价值)总价值对比 19 if goodsValues[i] < backp[j-1][i]: 20 goodsValues[i] = backp[j-1][i] 21 backp[j][i] = backp[j-1][i] 22 else: 23 backp[j][i] = goodsValues[i] 24 #判断截止到上一个物品总重量(装或不装的物品状态)即用下标(重量)与截止到当前被操作物品总重量之和是否超过总重量,不超过,则物品装进背包里面 25 if i+backValues[j][0]<(len(backp[j])): 26 #判断当前总重量的价值和与截止到上一个被操作物品总重量的价值+当前物品的价值之和对比,以便求出最大价值。 27 if goodsValues[i+backValues[j][0]] < backp[j-1][i] + backValues[j][1]: 28 goodsValues[i + backValues[j][0]] = backp[j-1][i] + backValues[j][1] 29 backp[j][i+backValues[j][0]] = backp[j-1][i] + backValues[j][1] 30 else: 31 backp[j][i + backValues[j][0]] = goodsValues[i + backValues[j][0]] 32 #lists[i+backValues[j][0]].append(backp[j][i] + backValues[j][1]) 33 34 35 for j in range(len(backp)): 36 37 for i in range(len(backp[j])): 38 39 #if backp[j][i] = 1 40 print(backp[j][i],end=" ") 41 print() 42 image =[[-1 for col in range(9)] for row in range(5)] 43 backpValues = np.array(image) 44 45 46 47 backWeightValues = [(3, 5), (2, 2), (1, 4), (1, 2), (4, 10)] 48 maxWeightValues(backpValues,backWeightValues)
输出结果:
0 -1 -1 5 -1 -1 -1 -1 -1 0 -1 2 5 -1 7 -1 -1 -1 0 4 2 6 9 7 11 -1 -1 0 4 6 6 9 11 11 13 -1 0 4 6 6 10 14 16 16 19



 浙公网安备 33010602011771号
浙公网安备 33010602011771号