基于非时序观察数据的因果关系发现综述 2017 计算机学报
基于非时序观察数据的因果关系发现
蔡瑞初,陈薇,张坤,郝志峰, 基于非时序观察数据的因果关系发现综述,2017， Vol.40,在线出版号 No.6
CAI Rui-Chu, CHEN Wei, ZHANG Kun, HAO Zhi-Feng, A Survey on Non-Temporal Series Observational Data based Causal Discovery, 2017,Vol.40,Online Publishing No.6
基于非时序观察数据的因果关系发现方法能够从被动观察获得的数据中发现变量之间的因果关系。
三大类方法
现有的因果模型与假设：
- 基于约束的方法
- 基于因果函数模型的方法
- 混合型方法
三个研究方向
- 因果关系方向推断
- 高维数据的误发现率控制
- 不完全观察数据的隐变量检测
三大类方法围绕着3个研究方向展开
实验工具
概括
基于约束的方法：
因果骨架学习->因果方向判断两个阶段
首先基于因果马尔科夫假设，采用条件独立性检验学习变量之间的因果骨架；
然后基于奥卡姆剃刀准则利用 V-结构确定因果方向
典型的算法：Peter-Clark 算法、 Inductive Causation 等
缺点：存在部分无法判断的因果关系方向， 即存在 Markov 等价类难题。
基于因果函数模型的方法：
- 基于数据的因果产生机制假设：噪声的非高斯性、原因变量与噪声的独立性、原因变量分布与因果函数梯度的独立性
- 构建变量之间的因果函数模型
典型的算法：
- 针对线性非高斯无环数据的Linear Non-Gaussian Acyclic Model算法
- 针对后非线性数据的Post-NonLinear算法
- 适用于非线性或离散数据的Additive Noise Model
缺点：需要较为严格的数据因果机制假设，ANM模型主要适用于低维数据
混合型方法：
- 基于约束的方法进行全局结构的学习
- 基于因果函数模型进行局部结构学习和方向判断
典型的算法：SADA、MCDSL
问题定义
给定\(p\)维变量集\(V=\{v_1,v_2,\ldots,v_p\}\)上的\(m\)组非时序观察数据\(X=\{ x_1,x_2,\ldots,x_m \}\);
发现变量集之间的因果关系。
隐变量：未能观察或无法度量的变量，一般体现为混淆因子（Confounder Variables）和选择偏倚（Selection Bias）[1]
[1]Spirtes P, Glymour C N, Scheines R. Causation, prediction, and search, second edition. Cambridge, USA: MIT press, 2000
因果假设
基本假设
Simon[12]指出， 从数据中决定因果结构的问题未被严格约束， 感知到的因果结构依赖于我们为其设定的先验假设。
Simon H A. Spurious correlation: A causal interpretation. Journal of the American Statistical Association, 1954, 49(267): 467-479
因果充分性假设(Causal Sufficiency Assumption)
当变量集\(V\)中的任意两个变量的直接原因变量都存在\(V\)中时， 变量集\(V\)就被认为是因果充分的。等价于外生变量（Exogenous variable）的独立性假设。
因果马尔可夫假设(Causal Markov Assumption)
对于具有因果充分性的变量集而言， 在已知变量的父亲节点的条件下，如果所有变量与他们的非后裔节点互相条件独立。
理解：假设所有变量之间的关系都是由因果关系引起的。简单化问题，其他的关系有：1. 共同后代的条件下产生条件依赖；第二是变量间的逻辑关系能产生非因果相关性，比如一年的销售量与4个季度的销量有关；3. 及时对称相互作用。
因果忠诚性假设(Causal Faithfulness Assumption)
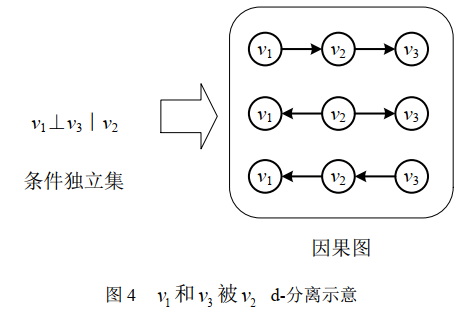
\(v_1\)和\(v_3\)之间的所有路径被变量集\(V\)中合适的变量\(v_2\) d-分离(d-separation) ，则所有随机变量的联合分布 P 与图 G 是因果忠诚的。保证变量之间不会出现额外的（条件）独立关系 。
数据产生方式假设
数据产生方式假设是为了提升因果关系发现能力，在最近的一系列因果关系方法中新引入的一类假设， 如数据类型的离散/连续、产生机制的线性/非线性/后线性、 噪声数据分布的无噪声/高斯/非高斯分布等。
