AC自动机

AC自动机

例题：AcWing 1282.搜索关键词

给定 n 个长度不超过 50 的由小写英文字母组成的单词，以及一篇长为 m 的文章。

请问，其中有多少个单词在文章中出现了。

思路：

这本质上是一个字符串匹配问题，有三种常用的字符串匹配：

1. Trie —— 文章中匹配字符串
2. KMP —— 单文本串单模式串匹配
3. AC自动机 —— 多文本串单模式串匹配

AC自动机 = Trie + KMP

什么是 AC自动机?

这是一棵 Trie $ \uparrow $

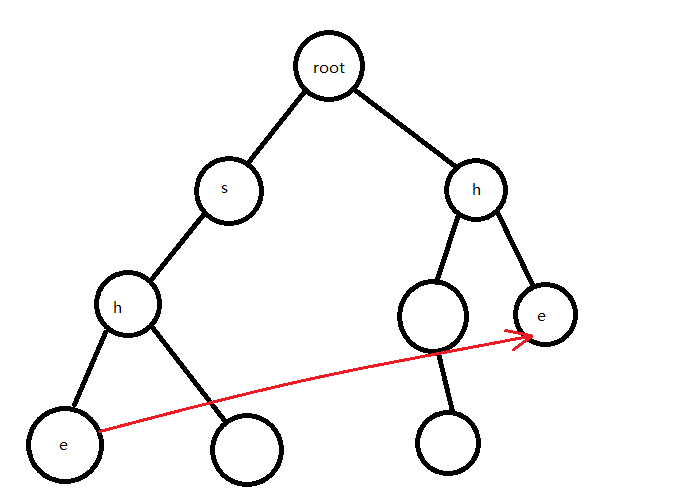
把它加上 \(ne\) 数组 $ \uparrow $

恭喜你，你构造了一个 AC自动机 才怪

如何构造

void build()
{
    hh = 0, tt = -1;
    for(int i = 0; i < 26; i ++)
        if(son[0][i])
            q[++ tt] = son[0][i];
    
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = 0; i < 26; i ++)
        {
            int& p = son[t][i];
            if(!p) p = son[ne[t]][i];
            else
            {
                ne[p] = son[ne[t]][i];
                q[++ tt] = p;
            }
        }
    }
}

讲完了咳咳，首先，我们要知道 KMP 的构造思路：
从 \(1 \sim n\) 开始，挨个进行找 \(ne\)
so,我们也可以以此类推，一层一层的找 \(ne\)

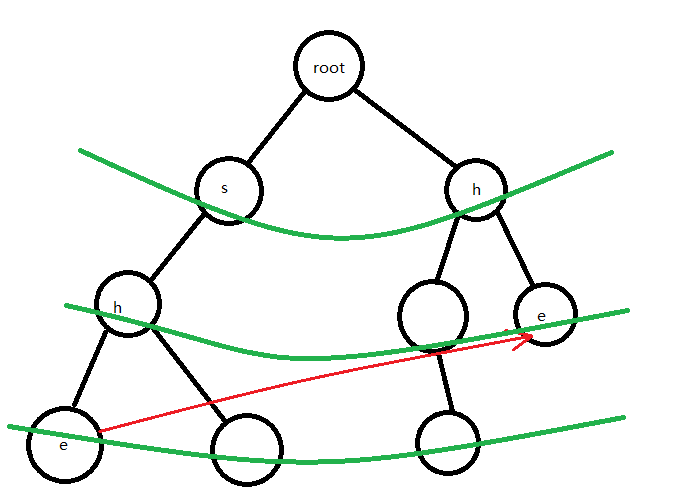
按绿色一圈一圈找 $ \uparrow $
所以，我们可以用 \(bfs\) 来进行计算 \(ne\) 数组

for(int i = 0; i < 26; i ++)
        if(son[0][i])
            q[++ tt] = son[0][i];
//将第一层添加入队列中

while(hh <= tt)
{
	int t = q[hh ++];//取出队头
	for(int i = 0; i < 26; i ++)//枚举
	{
		int& p = son[t][i];//取别名，简化代码
		if(!p) p = son[ne[t]][i];//1
		else
		{
			ne[p] = son[ne[t]][i];//2
			q[++ tt] = p;
		}
	}
}

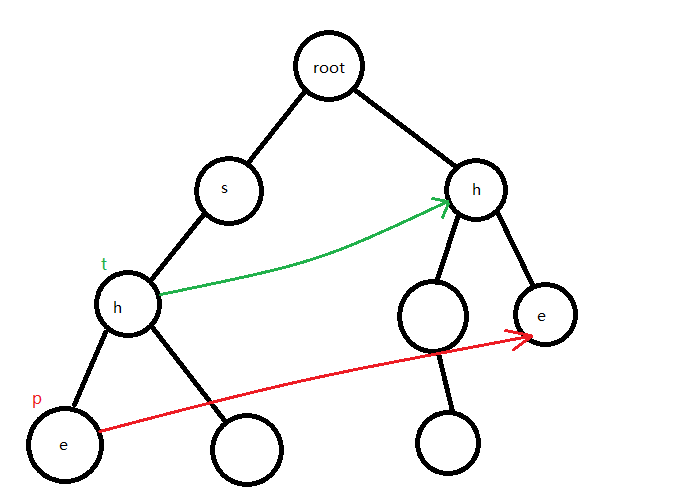
\(1\)：在匹配部分详解

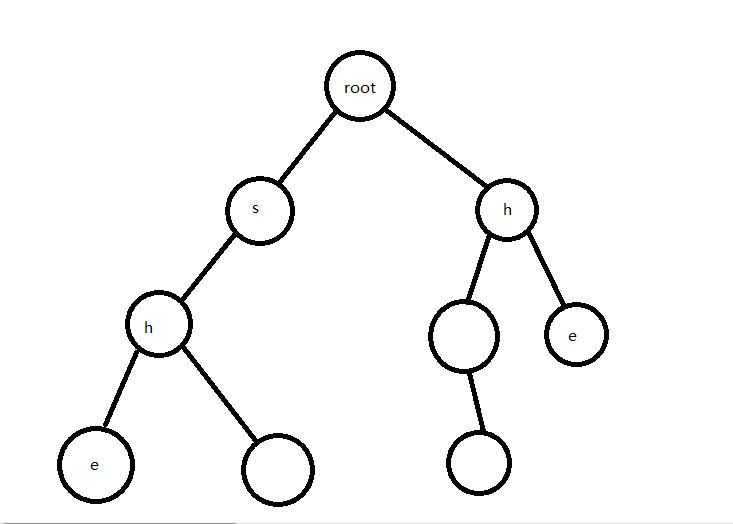
\(2\)：如图，\(t\) 在 \(^"h^"\) 处，\(ne_t\) 在绿箭头指向处；

执行 ne[p] = son[ne[t]][i];， \(ne_p\) 指向红箭头处，代表如果在 \(p\) 处不匹配，跳到 \(ne_p\) 处继续匹配
执行 q[++ tt] = p;，将 \(p\) ，或者说 \(son_{t,i}\) 加入候选队列中

如何匹配

现在，我们已经找到了 \(ne\) 数组，下一步就是开始匹配

void doit()
{
    int res = 0;
    
    for(int i = 0, j = 0; str[i]; i ++)
    {
        int t = str[i] - 'a';
        
        j = son[j][t];
        
        int p = j;
        
        while(p && cnt[p] != -1)
        {
            res += cnt[p];
            cnt[p] = -1;
            p = ne[p];
        }
        
    }
    
    cout << res << "\n";
}

\(i\)：文本串上的指针

\(j\)：树上的指针

int res = 0;

设置答案初始值

 for(int i = 0, j = 0; str[i]; i ++)

循环遍历文本串

int t = str[i] - 'a';

设置当前字符的编号

j = son[j][t];

\(j\) 指向下一个该匹配的字符 （为什么不会匹配失败？）不急，等会讲

int p = j;
        
while(p && cnt[p] != -1)
{
    res += cnt[p];
    cnt[p] = -1;
    p = ne[p];
}

开始匹配，设置 \(p\) 为临时指针，每一次加上以当前节点结尾的模式串数量， \(cnt_p = -1\) 是为了防止重复， \(p\) 跳到下一个

cout << res << "\n";

输出

回到那个问题，if(!p) p = son[ne[t]][i]; 有什么用以及 j = son[j][t]; 为什么不会匹配失败

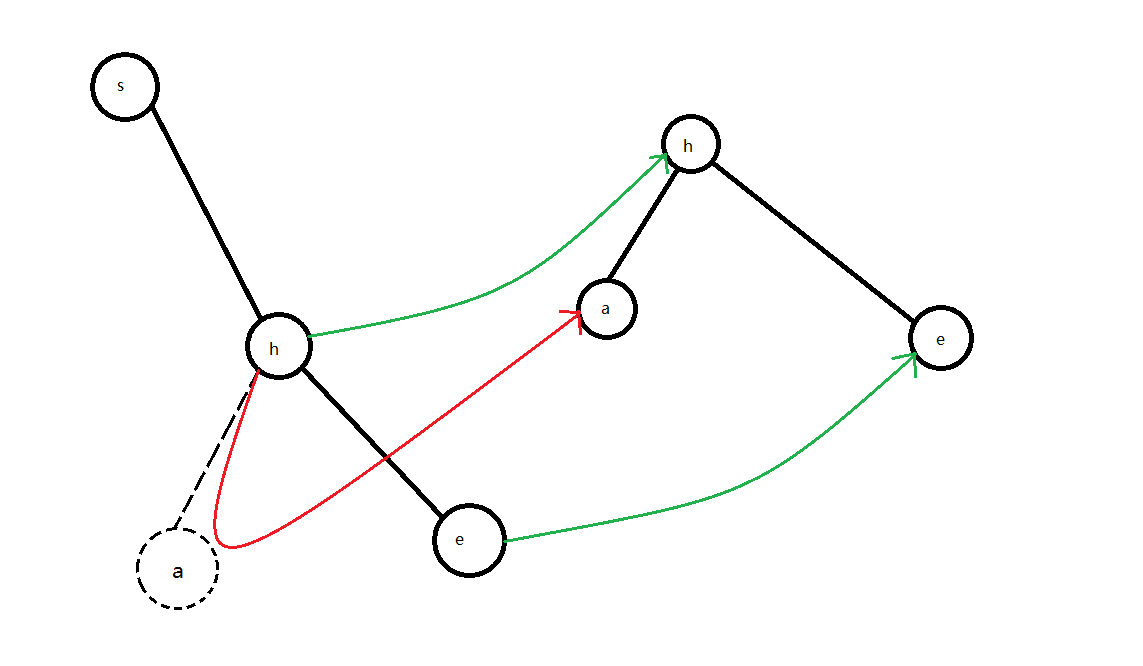
在 \(p == 0\) 处，如图，\(\uparrow p\) 本该指向这，可没有，所以连到 \(son_{ne_t, i}\) 上，这样可以让每一个 \(son\) 都有值，解决了匹配失败的问题

code

#include <bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10, M = 1e6 + 10, S = 55;

int ne[N * S], n;
int son[N * S][26], cnt[N * S], idx;
int q[N * S], hh, tt;
char str[M];

void insert()
{
    int p = 0;
    for(int i = 0; str[i]; i ++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++;
}

void build()
{
    hh = 0, tt = -1;
    
    for(int i = 0; i < 26; i ++)
        if(son[0][i])
            q[++ tt] = son[0][i];
    
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = 0; i < 26; i ++)
        {
            int& p = son[t][i];
            
            if(!p) p = son[ne[t]][i];
            else
            {
                ne[p] = son[ne[t]][i];
                q[++ tt] = p;
            }
        }
    }
    
}

void doit()
{
    int res = 0;
    
    for(int i = 0, j = 0; str[i]; i ++)
    {
        int t = str[i] - 'a';
        
        j = son[j][t];
        
        int p = j;
        
        while(p && cnt[p] != -1)
        {
            res += cnt[p];
            cnt[p] = -1;
            p = ne[p];
        }
        
    }
    
    cout << res << "\n";
}

int main()
{
    
    int T;
    cin >> T;
    
    while(T --)
    {
        memset(ne, 0, sizeof ne);
        memset(cnt, 0, sizeof cnt);
        memset(son, 0, sizeof son);
        idx = 0;
        
        cin >> n;
        
        for(int i = 1; i <= n; i ++)
        {
            cin >> str;
            insert();
        }
        
        build();
        
        cin >> str;
        
        doit();
        
    }
    
    return 0;
}