笔记：对抗训练及其在Bert中的应用

最近在打一个比赛，发现往年的优秀样例都添加了对抗训练和多模型融合，遂学习一下对抗训练，并在实际比赛中检验效果

对抗样本的基本概念

要认识对抗训练，首先要了解 "对抗样本"，它首先出现在论文 Intriguing properties of neural networks 之中。简单来说，它是指对于人类来说 "看起来" 几乎一样，但对于模型来说预测结果却完全不一样的样本，比如下面的经典例子（一只熊猫加了点扰动就被识别成了长臂猿）

那么什么样的样本才是最好的对抗样本呢？

对抗样本一般需要具备两个特点：

相对于原始输入，所添加的扰动是微小的
能使模型犯错

对抗训练基本概念

GAN之父Goodfellow在15年的ICLR中第一次提出了对抗训练这个概念，简而言之，就是在原始输入样本 $x$ 上加上一个扰动 $\Delta x$ 得到对抗样本，再用其进行训练。

也就是说，这个问题可以抽象成这样一个模型：

$$\max _{\theta} P(y \mid x+\Delta x ; \theta)$$

其中，$y$ 是 ground truth, $\theta$ 是模型参数。意思就是即使在扰动的情况下求使得预测出 $y$ 的概率最大的参数 $\theta$.

那扰动 $\Delta x$ 是如何确定的呢？

GoodFellow认为：神经网络由于其线性的特点，很容易受到线性扰动的攻击。于是他提出了 Fast Gradinet Sign Method (FGSM)，来计算输入样本的扰动。扰动可以被定义为

$$\Delta x=\epsilon \cdot \operatorname{sgn}\left(\nabla_{x} L(x, y ; \theta)\right)$$

其中，$sgn$ 为符号函数，$L$ 为损失函数（很多地方也用 $J$ 来表示）。GoodFellow发现 $\epsilon = 0.25$ 时，这个扰动能给一个单层分类器造成99.9%的错误率。这个扰动其实就是沿着梯度反方向走了 $\Delta x$

最后，GoodFellow还总结了对抗训练的两个作用：

1. 提高模型应对恶意对抗样本时的鲁棒性

2. 作为一种regularization，减少overfitting，提高泛化能力

Min-Max公式

Madry在2018年的ICLR论文 Towards Deep Learning Models Resistant to Adversarial Attacks 中总结了之前的工作。总的来说，对抗训练可以统一写成如下格式：

$$\min _{\theta} \mathbb{E}_{(x, y) \sim \mathcal{D}}\left[\max _{\Delta x \in \Omega} L(x+\Delta x, y ; \theta)\right]$$

其中 $\mathcal{D}$ 代表输入样本的分布，$x$ 代表输入，$y$ 代表标签，$\theta$ 是模型参数，$L(x+y; \theta)$ 是单个样本的loss，$\Delta x$ 是扰动，$\Omega$ 是扰动空间。这个式子可以分布理解如下：

1. 内部max是指往 $x$ 中添加扰动 $\Delta x$，$\Delta x$ 的目的是让 $L(x+\Delta x, y ; \theta)$ 越大越好，也就是说尽可能让现有模型预测出错。但是，$\Delta x$ 也是有约束的，要在 $\Omega$ 范围内. 常规的约束是 $|| \Delta x|| \leq \epsilon$，其中 $\epsilon$ 是一个常数

2. 外部min是指找到最鲁棒的参数 $\theta$ 是预测的分布符合原数据集的分布

这就解决了两个问题：如何构建足够强的对抗样本、和如何使得分布仍然尽可能接近原始分布

从CV到NLP

对于CV领域，图像可以认为是连续的，因此可以直接在原始图像上添加扰动；

而对于NLP，它的输入时文本，本质是one-hot，而两个one-hot之间的欧式距离恒为 $\sqrt{2}$，理论上不存在“微小的扰动”，

而且，在Embedding向量上加上微小扰动可能就找不到与之对应的词了，这就不是真正意义上的对抗样本了，因为对抗样本依旧能对应一个合理的原始输入

既然不能对Embedding向量添加扰动，可以对Embedding层添加扰动，使其产生更鲁棒的Embedding向量

Fast Gradient Method（FGM）

上面提到，Goodfellow 在 15 年的 ICLR 中提出了 Fast Gradient Sign Method（FGSM），随后，在 17 年的 ICLR 中，Goodfellow 对 FGSM 中计算扰动的部分做了一点简单的修改。假设输入文本序列的 Embedding vectors 为 $x$，Embedding层的扰动为：

\begin{aligned}
\Delta x &=\epsilon \cdot \frac{g}{\|g\|_{2}} \\
g &=\nabla_{x} L(x, y ; \theta)
\end{aligned}

实际上就是取消了符号函数，用二范式做了一个 scale，需要注意的是这里norm计算是针对一个sample，对梯度 $g$ 的后两维计算norm，为了方便，这里是对一个batch计算norm。其实除以norm本来就是一个放缩作用，影响不大。假设 $x$ 的维度是 $[batch\_size, len, embed_size]$，针对sample计算的norm是 $[batch\_size, 1, 1]$，针对整个batch计算的norm是 $[1, 1, 1]$。

class FGM():
    def __init__(self, model):
        self.model = model
        self.backup = {}

    def attack(self, epsilon=1., emb_name='emb'):
        # emb_name这个参数要换成你模型中embedding的参数名
        # 例如，self.emb = nn.Embedding(5000, 100)
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                self.backup[name] = param.data.clone()
                norm = torch.norm(param.grad) # 默认为2范数
                if norm != 0:
                    r_at = epsilon * param.grad / norm
                    param.data.add_(r_at)

    def restore(self, emb_name='emb'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.backup
                param.data = self.backup[name]
        self.backup = {}

需要使用对抗训练的时候，只需要添加5行代码：

# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
  # 正常训练
  loss = model(batch_input, batch_label)
  loss.backward() # 反向传播，得到正常的grad

  # 对抗训练
  fgm.attack() # embedding被修改了
  # optimizer.zero_grad() # 如果不想累加梯度，就把这里的注释取消
  loss_sum = model(batch_input, batch_label)
  loss_sum.backward() # 反向传播，在正常的grad基础上，累加对抗训练的梯度
  fgm.restore() # 恢复Embedding的参数
  # 梯度下降，更新参数
  optimizer.step()
  optimizer.zero_grad()

Note: 不是把上面的正常训练换成对抗训练，而是两者都要，先正常训练再对抗训练

Projected Gradient Descent（PGD）

FGM 的思路是梯度上升，本质上来说没有什么问题，但是 FGM 简单粗暴的 "一步到位" 是不是有可能并不能走到约束内的最优点呢？当然是有可能的。于是，一个新的想法诞生了，Madry 在 18 年的 ICLR 中提出了 Projected Gradient Descent（PGD）方法，简单的说，就是 "小步走，多走几步"，如果走出了扰动半径为

\begin{aligned}
x_{t+1} &=\prod_{x+S}\left(x_{t}+\alpha \frac{g\left(x_{t}\right)}{\left\|g\left(x_{t}\right)\right\|_{2}}\right) \\
g\left(x_{t}\right) &=\nabla_{x} L\left(x_{t}, y ; \theta\right)
\end{aligned}

其中$S=\left\{r \in \mathbb{R}^{d}:\|r\|_{2} \leq \epsilon\right\}$ 为扰动的约束空间，$\alpha$ 是小步的步长

由于 PGD 理论和代码比较复杂，因此下面先给出伪代码方便理解，然后再给出代码

对于每个x:
  1.计算x的前向loss，反向传播得到梯度并备份
  对于每步t:
    2.根据Embedding矩阵的梯度计算出r，并加到当前Embedding上，相当于x+r（超出范围则投影回epsilon内）
    3.t不是最后一步: 将梯度归0，根据(1)的x+r计算前后向并得到梯度
    4.t是最后一步: 恢复(1)的梯度，计算最后的x+r并将梯度累加到(1)上
  5.将Embedding恢复为(1)时的值
  6.根据(4)的梯度对参数进行更新

可以看到，在循环中

class PGD():
    def __init__(self, model):
        self.model = model
        self.emb_backup = {}
        self.grad_backup = {}

    def attack(self, epsilon=1., alpha=0.3, emb_name='emb', is_first_attack=False):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0:
                    r_at = alpha * param.grad / norm
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data, epsilon)

    def restore(self, emb_name='emb'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}
        
    def project(self, param_name, param_data, epsilon):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > epsilon:
            r = epsilon * r / torch.norm(r)
        return self.emb_backup[param_name] + r
        
    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                self.grad_backup[name] = param.grad.clone()
    
    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                param.grad = self.grad_backup[name]

使用的时候要麻烦一点：

pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    loss.backward() # 反向传播，得到正常的grad
    pgd.backup_grad() # 保存正常的grad
    # 对抗训练
    for t in range(K):
        pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
        if t != K-1:
            optimizer.zero_grad()
        else:
            pgd.restore_grad() # 恢复正常的grad
        loss_sum = model(batch_input, batch_label)
        loss_sum.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
    pgd.restore() # 恢复embedding参数
    # 梯度下降，更新参数
    optimizer.step()
    optimizer.zero_grad()

Virtual Adversarial Training

除了监督任务，对抗训练还可以用在半监督任务中，尤其对于 NLP 任务来说，很多时候我们拥有大量的未标注文本，那么就可以参考 Distributional Smoothing with Virtual Adversarial Training 进行半监督训练

首先，抽取一个随机标准正态扰动 $\left(d \sim \mathcal{N}(0,1) \in \mathbb{R}^{d}\right)$，加到Embedding上，并用KL散度计算梯度：

\begin{aligned}
g &=\nabla_{x^{\prime}} D_{K L}\left(p(\cdot \mid x ; \theta)|| p\left(\cdot \mid x^{\prime} ; \theta\right)\right) \\
x^{\prime} &=x+\xi d
\end{aligned}

然后，用得到的梯度，计算对抗扰动，并进行对抗训练：

\begin{aligned}
&\min _{\theta} D_{K L}\left(p(\cdot \mid x ; \theta)|| p\left(\cdot \mid x^{*} ; \theta\right)\right) \\
&x^{*}=x+\epsilon \frac{g}{\|g\|_{2}}
\end{aligned}

实现起来有很多细节，并且笔者对于 NLP 的半监督任务了解并不多，因此这里就不给出实现了

实验对照

为了说明对抗训练的作用，网上有位大佬选了四个 GLUE 中的任务进行了对照试验，实验代码使用的 Huggingface 的 transformers/examples/run_glue.py，超参都是默认的，对抗训练用的也是相同的超参

任务	Metrics	BERT-Base	FGM	PGD
MRPC	Accuracy	83.6	86.8	85.8
CoLA	Matthew's corr	56.0	56.0	56.8
STS-B	Person/Spearmean corr	89.3/88.8	89.3/88.8	89.3/88.8
RTE	Accuracy	64.3	66.8	64.6

可以看出，对抗训练还是有效的，在 MRPC 和 RTE 任务上甚至可以提高三四个百分点。不过，根据我们使用的经验来看，是否有效有时也取决于数据集

为什么对抗训练有效

Adversarial Training 能够提升 Word Embedding 质量的一个原因是：

有些词与比如（good 和 bad），其在语句中 Grammatical Role 是相近的，我理解为词性相同（都是形容词），并且周围一并出现的词语也是相近的，比如我们经常用来修饰天气或者一天的情况（The weather is good/bad; It's a good/bad day），这些词的 Word Embedding 是非常相近的。文章中用 Good 和 Bad 作为例子，找出了其最接近的 10 个词：

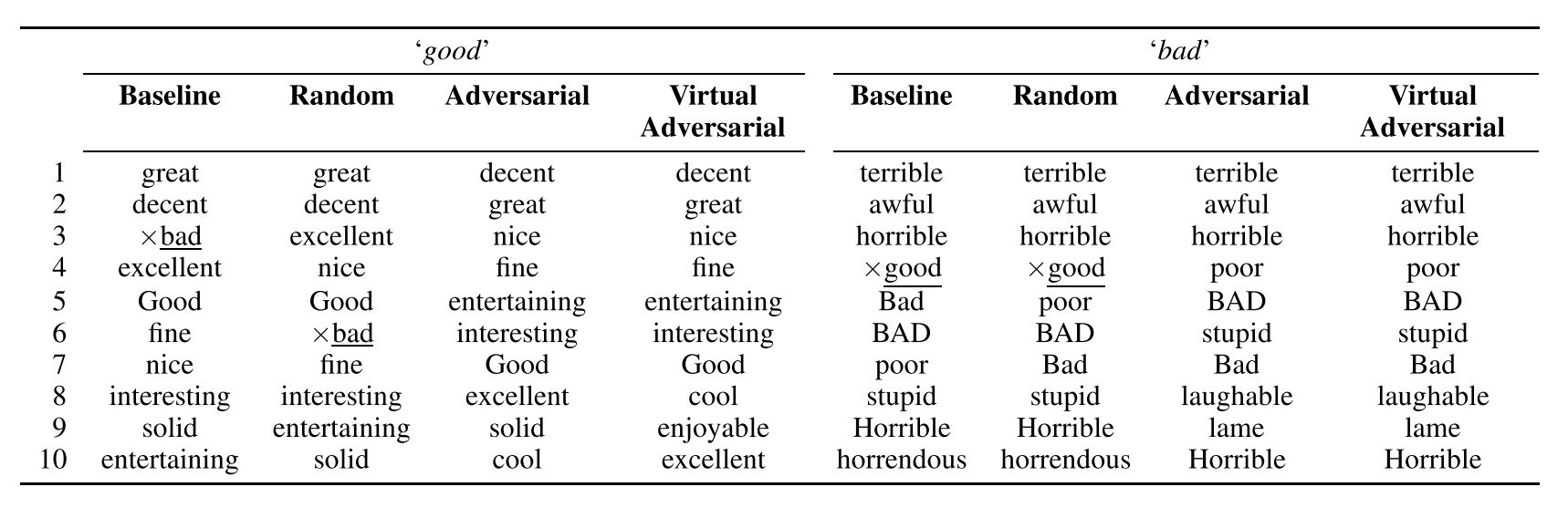
可以发现在 Baseline 和 Random 的情况下，good 和 bad 出现在了彼此的邻近词中，而喂给模型经过扰动之后的 X-adv 之后，也就是 Adversarial 这一列，这种现象就没有出现，事实上， good 掉到了 bad 接近程度排第 36 的位置

我们可以猜测，在 Word Embedding 上添加的 Perturbation 很可能会导致原来的 good 变成 bad，导致分类错误，计算的 Adversarial Loss 很大，而计算 Adversarial Loss 的部分是不参与梯度计算的，也就是说，模型（LSTM 和最后的 Dense Layer）的 Weight 和 Bias 的改变并不会影响 Adversarial Loss，模型只能通过改变 Word Embedding Weight 来努力降低它，进而如文章所说：

Adversarial training ensures that the meaning of a sentence cannot be inverted via a small change, so these words with similar grammatical role but different meaning become separated.

这些含义不同而语言结构角色类似的词能够通过这种 Adversarial Training 的方法而被分离开，从而提升了 Word Embedding 的质量，帮助模型取得了非常好的表现

梯度惩罚

这一部分，我们从另一个视角对上述结果进行分析，从而推出对抗训练的另一种方法，并且得到一种关于对抗训练更直观的几何理解

假设已经得到对抗扰动 $\Delta x$，更新 $\theta$ 时，对 $L$ 进行泰勒展开：

\begin{aligned}
\min _{\theta} \mathbb{E}_{(x, y) \sim D}[L(x+\Delta x, y ; \theta)] & \approx \min _{\theta} \mathbb{E}_{(x, y) \sim D}\left[L(x, y ; \theta)+<\nabla_{x} L(x, y ; \theta), \Delta x>\right] \\
&=\min _{\theta} \mathbb{E}_{(x, y) \sim D}\left[L(x, y ; \theta)+\nabla_{x} L(x, y ; \theta) \cdot \Delta x\right] \\
&=\min _{\theta} \mathbb{E}_{(x, y) \sim D}\left[L(x, y ; \theta)+\nabla_{x} L(x, y ; \theta)^{T} \Delta x\right]
\end{aligned}

对应的 $\theta$ 的梯度为：

$$\nabla_{\theta} L(x, y ; \theta)+\nabla_{\theta} \nabla_{x} L(x, y ; \theta)^{T} \Delta x$$

将 $\Delta x=\epsilon \nabla_{x} L(x, y ; \theta)$ 代入：

\begin{aligned}
&\nabla_{\theta} L(x, y ; \theta)+\epsilon \nabla_{\theta} \nabla_{x} L(x, y ; \theta)^{T} \nabla_{x} L(x, y ; \theta) \\
&=\nabla_{\theta}\left(L(x, y ; \theta)+\frac{1}{2} \epsilon\left\|\nabla_{x} L(x, y ; \theta)\right\|^{2}\right)
\end{aligned}

这个结果表示，对输入样本添加 $\epsilon \nabla x L(x, y ; \theta)$ 的对抗扰动，一定程度上等价于往loss中加“梯度惩罚”

$$\frac{1}{2} \epsilon\left\|\nabla_{x} L(x, y ; \theta)\right\|^{2}$$

如果对抗扰动是 $\epsilon\|\nabla x L(x, y ; \theta)\|$，那么对应的梯度惩罚项是 $\epsilon\|\nabla x L(x, y ; \theta)\|$ （少了个1/2，也少了个2次方）。

几何解释

事实上，关于梯度惩罚，我们有一个非常直观的几何图像。以常规的分类问题为例，假设有n个类别，那么模型相当于挖了n个坑，然后让同类的样本放到同一个坑里边去：

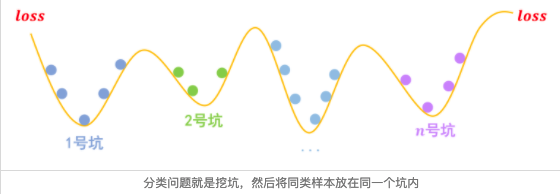
梯度惩罚则说“同类样本不仅要放在同一个坑内，还要放在坑底”，这就要求每个坑的内部要长这样：

为什么要在坑底呢？因为物理学告诉我们，坑底最稳定呀，所以就越不容易受干扰呀，这不就是对抗训练的目的么？

那坑底意味着什么呢？极小值点呀，导数（梯度）为零呀，所以不就是希望 $‖∇xL(x,y;θ)‖‖∇xL(x,y;θ)‖$ 越小越好么？这便是梯度惩罚的几何意义了。

验证部分

将对抗训练加到项目中，出了点小问题，待修改

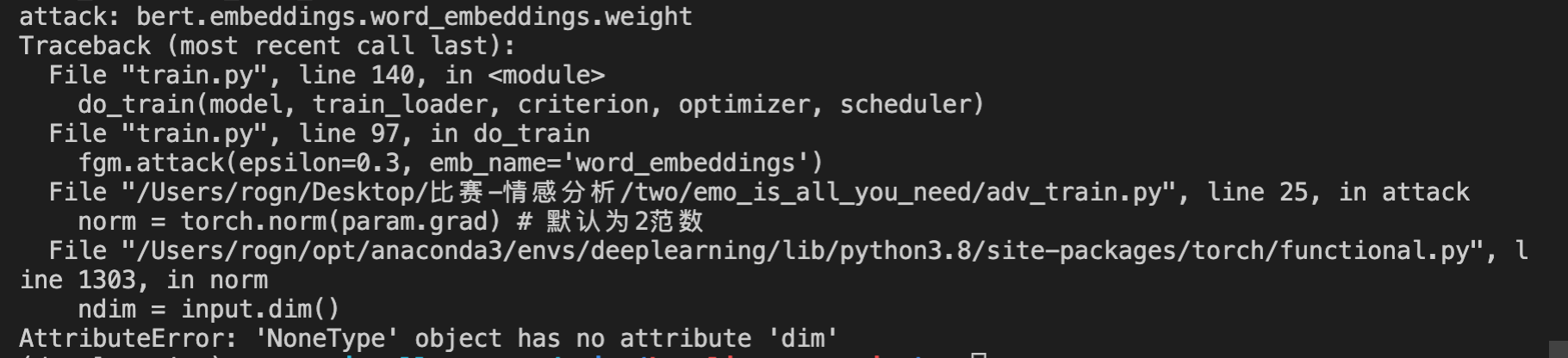
不知道为啥grad=None??

参考链接：

https://wmathor.com/index.php/archives/1537/

https://coding-zuo.github.io/2021/04/07/nlp中的对抗训练-与bert结合/

https://zhuanlan.zhihu.com/p/91269728

论文：

Adversarial Training for Aspect-Based Sentiment Analysis with BERT

FGSM: Explaining and Harnessing Adversarial Examples

FGM: Adversarial Training Methods for Semi-Supervised Text Classification

FreeAT: Adversarial Training for Free!

YOPO: You Only Propagate Once: Accelerating Adversarial Training via Maximal Principle

FreeLB: Enhanced Adversarial Training for Language Understanding

SMART: Robust and Efficient Fine-Tuning for Pre-trained Natural

代码

https://blog.csdn.net/weixin_42001089/article/details/115458615

https://github.com/bojone/keras_adversarial_training

https://github.com/bojone/bert4keras/blob/master/examples/task_iflytek_adversarial_training.py

posted @ 2021-11-09 19:11 Rogn 阅读(1710) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Rogn