矩形覆盖

题目描述：我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形，总共有多少种方法？比如 n=3 时，2*3 的矩形块有 3 种覆盖方法：

 

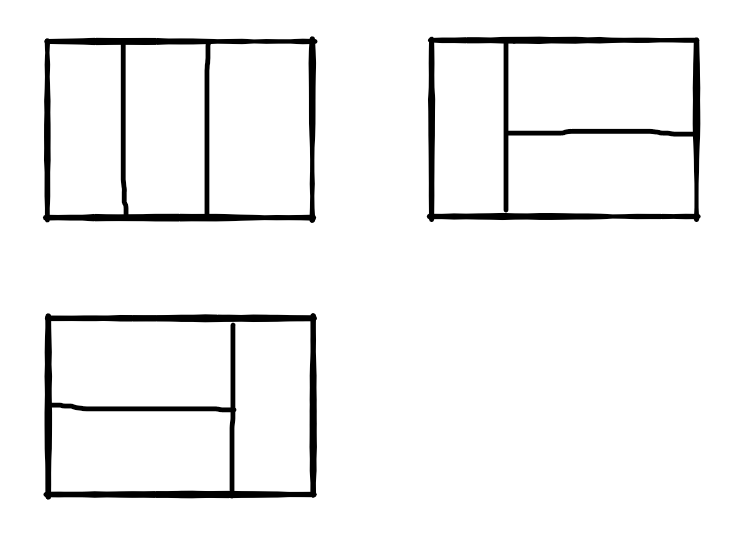
分析：涂掉最后一级矩形的时候，是用什么方式完成的？

• n = 1 的时候
  • 只能横着覆盖，一种
• n = 2 的时候
  • 可以横着和竖着覆盖，两种
• n = 3 的时候
  • 第三级横着覆盖，用了一级，剩下 n = 2，有两种覆盖方法
  • 第三级竖着覆盖，用了两级，剩下 n = 1，有一种覆盖方法
  • 总共有 3 种
• n = 4 的时候
  • 第 4 级横着覆盖，用了一级，剩下 n = 3，有三种覆盖方法
  • 第 4 级竖着覆盖，用了两级，剩下 n = 2，有两种覆盖方法
  • 总共有 5 种方法
• n = n 的时候
  • 第 n 级横着覆盖，用了一级，剩下 n = n - 1，所以关注第 n - 1 种有几种覆盖方法
  • 第 n 级竖着覆盖，用了两级，剩下 n = n - 2，所以关注第 n - 2 种有几种覆盖方法
  • 总和为两种情况的总和 

PS：与牛客相同！

public class Solution {
    public int RectCover(int target) {
        if(target < 1) {
            return 0;
        } else if(target == 1 || target == 2) {
            return target;
        } else {
            #  return RectCover(target - 1) + RectCover(target - 2);
            int a = 1, b = 2, c = 0;
            for(int i = 3; i <= target; i++) {
                c = a + b;
                a = b;
                b = c;
            }
            return c;
        }
    }
}