整数中 1 出现的次数（从 1 到 n 整数中 1 出现的次数）

题目描述：求出 1~13 的整数中 1 出现的次数,并算出 100~1300 的整数中1出现的次数？为此他特别数了一下 1~13 中包含1的数字有 1、10、11、12、13 因此共出现 6 次,但是对于后面问题他就没辙了。ACMer 希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中 1 出现的次数（从1 到 n 中1出现的次数）。

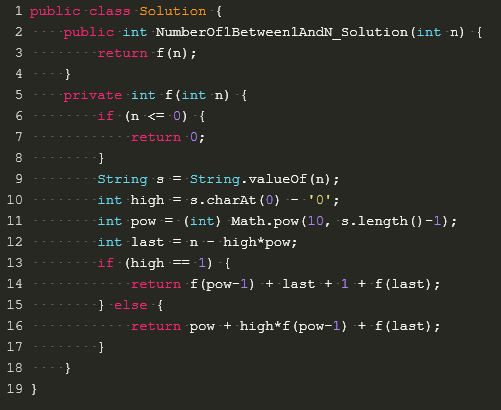
分析：f(n) 函数的意思是1～n 这 n 个整数的十进制表示中 1 出现的次数，将 n 拆分为两部分，最高一位的数字 high 和其他位的数字 last，分别判断情况后将结果相加，看例子更加简单。

例1： n=1234，high=1, pow=1000, last=234
可以将数字范围分成两部分 1~999 和 1000~1234

1~999 这个范围 1 的个数是 f(pow-1)
1000~1234 这个范围 1 的个数需要分为两部分：

千分位是1的个数：千分位为 1 的个数刚好就是 234+1(last+1)，注意，这儿只看千分位，不看其他位
其他位是1的个数：即是 234 中出现 1 的个数，为 f(last)

所以全部加起来是f(pow-1) + last + 1 + f(last);

 

例2：3234，high=3, pow=1000, last=234
可以将数字范围分成两部分 1~999，1000~1999，2000~2999 和 3000~3234

1~999 这个范围 1 的个数是 f(pow-1)
1000~1999 这个范围1的个数需要分为两部分：

千分位是1的个数：千分位为 1 的个数刚好就是 pow，注意，这儿只看千分位，不看其他位
其他位是1的个数：即是 999 中出现1的个数，为 f(pow-1)

2000~2999 这个范围 1 的个数是 f(pow-1)
3000~3234 这个范围 1 的个数是 f(last)

所以全部加起来是 pow + high*f(pow-1) + f(last);

 

PS：与牛客相同！

代码：