变态跳台阶

题目描述：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级……它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

分析：

f(n) = f(n - 1) + f(n - 2) + ...... + f(1)

f(n - 1) = f(n - 2) + ...... + f(1)

两式相减得：f(n) = 2f(n - 1)，而 f(1) = 1，所以 f(n) = pow(2, n - 1)。

• 若楼梯阶级 n = 3

  • 跳 3 步到 3：没有剩下步数没跳的，只有这样一种跳法
  • 跳 2 步到 3：剩下的是第一步没跳，起始跳到第一步只有一种
  • 跳 1 步到 3：剩下的是第二步没跳，起始跳到第二步有两种

  求得，n = 3 时，有 4 种跳法

• 若楼梯阶级 n = 4

  • 跳 4 步到 4：没有剩下步数没跳的，只有这样一种跳法
  • 跳 3 步到 4：剩下的是第一步没跳，起始跳到第一步只有一种
  • 跳 2 步到 4：剩下的是第二步没跳，起始跳到第二步只有两种
  • 跳 1 步到 4：剩下的是第三步没跳，起始跳到第三步有四种

  求得，n = 4 时，有 8 种跳法

• 若楼梯阶级 n = n

  • 跳 x 步到 n 有几种的和，跟前 n - 1 种状态有关

PS：与牛客相同！

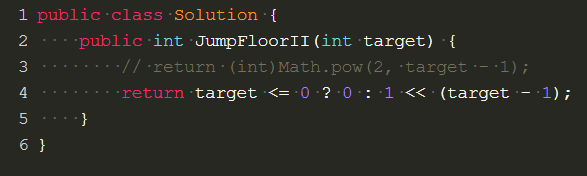
代码：