二叉搜索树的后序遍历序列

题目描述：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。

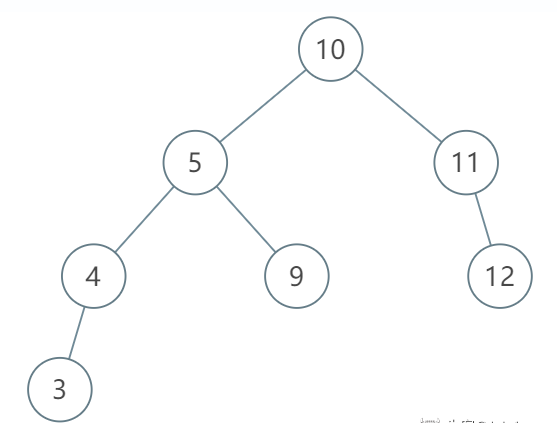
分析：如图，一棵 BST ：左孩子 < 根结点 < 右孩子，一棵 BST 的左子树或者右子树都是 BST。

后序遍历是，左右根：[3, 4, 9, 5, 12, 11, 10]，结合图再从左往右分析后序序列，分析子树，可以发现：

[3, 4, 9, 5] 10 [12, 11]

• [3, 4] 5 [9]
  • [3] 4
• [12] 11

发现对于每一棵子树，它的根结点总是对应该子树的后序序列的最后一个数，

那么，只需要不断地确定出左子树区间和右子树区间，并且判断：左子树区间的所有结点值 < 根结点值 < 右子树区间所有结点值，这个条件是否满足即可。

 

 

PS：与牛客相同！

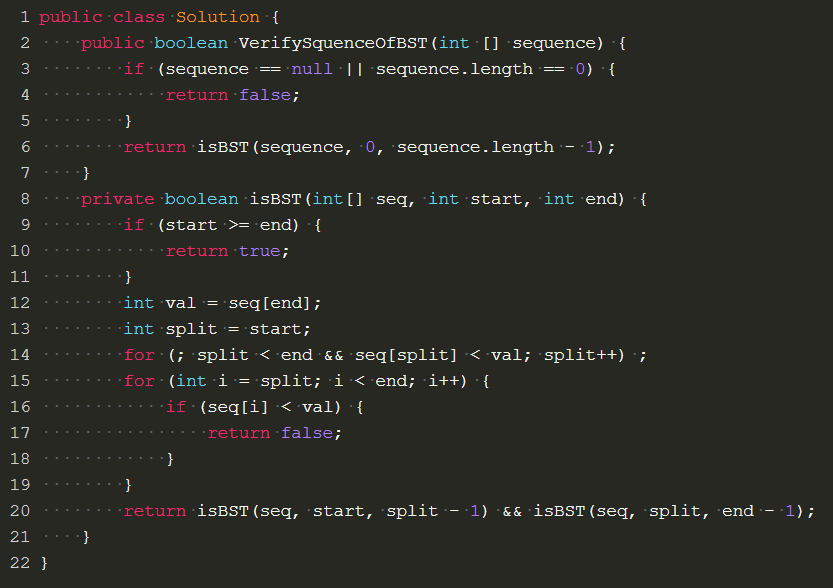
代码：

 

第二种解法：二叉树的中序序列和后序序列满足栈的压入弹出序列关系，即如果把中序序列当做栈的压入序列，那么后序序列是该栈的一个弹出序列。而BST的中序是排序数组。因此将本题的序列排序作为中序序列，判断两序列是否满足上述关系即可。

 

import java.util.Stack;
import java.util.Arrays;
 
public class Solution {
    public boolean VerifySquenceOfBST(int [] seq) {
        int[] arr = seq.clone();
        Arrays.sort(arr);
        return IsPopOrder(arr,seq);
         
    }
//判断第二个序列是否可能为第一个序列的弹出顺序,引用的“栈的压入、弹出序列”题目的答案
public boolean IsPopOrder(int [] pushA,int [] popA) {
        if(pushA.length == 0 || popA.length == 0)
            return false;
        Stack<Integer> s = new Stack<Integer>();
        //用于标识弹出序列的位置
        int popIndex = 0;
        for(int i = 0; i< pushA.length;i++){
            s.push(pushA[i]);
            //如果栈不为空，且栈顶元素等于弹出序列
            while(!s.empty() &&s.peek() == popA[popIndex]){
                //出栈
                s.pop();
                //弹出序列向后一位
                popIndex++;
            }
        }
        return s.empty();
    }
}