剪绳子

题目描述：给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1，m<=n），每段绳子的长度记为k[1],...,k[m]。请问k[1]x...xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为 2、3、3 的三段，此时得到的最大乘积是18。

解题思路：找出最优解的规律

* 当 target 等于1，2，3的时候，结果是固定的
* 当 target 大于3的时候，可以看以下数据
* target = 4, 最优解：2 2
* target = 5, 最优解：3 2
* target = 6, 最优解：3 3
* target = 7, 最优解：3 2 2
* target = 8, 最优解：3 3 2
* target = 9, 最优解：3 3 3
* target = 10,最优解：3 3 2 2
* target = 11,最优解：3 3 3 2
* target = 12,最优解：3 3 3 3
* target = 13,最优解：3 3 3 2 2
* target = 14,最优解：3 3 3 3 2
* target = 15,最优解：3 3 3 3 3

* 所以不难发现 3 和 2 的个数规律

PS：与牛客相同！

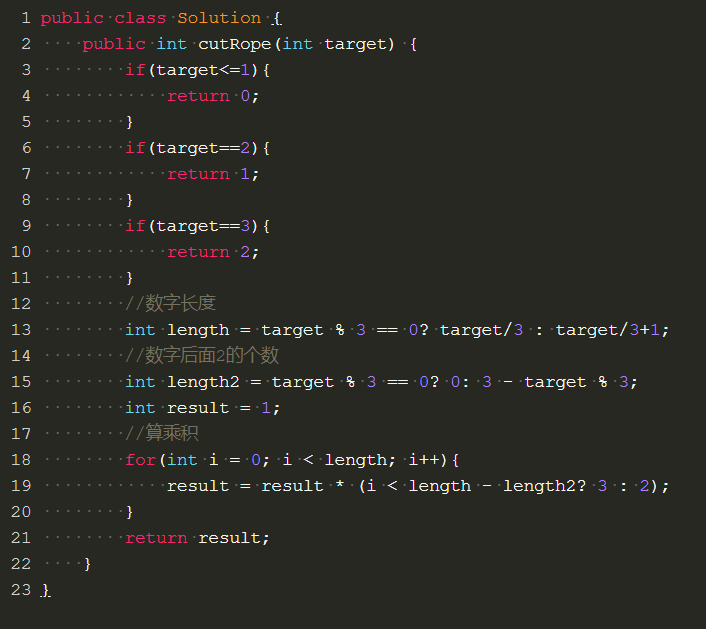
代码：