59. 螺旋矩阵 II 模拟过程

59. 螺旋矩阵 II
思路
用代码模拟出顺时针填充数字的过程。
每填充一圈涉及4条边：顶部、右列、底部、左列。

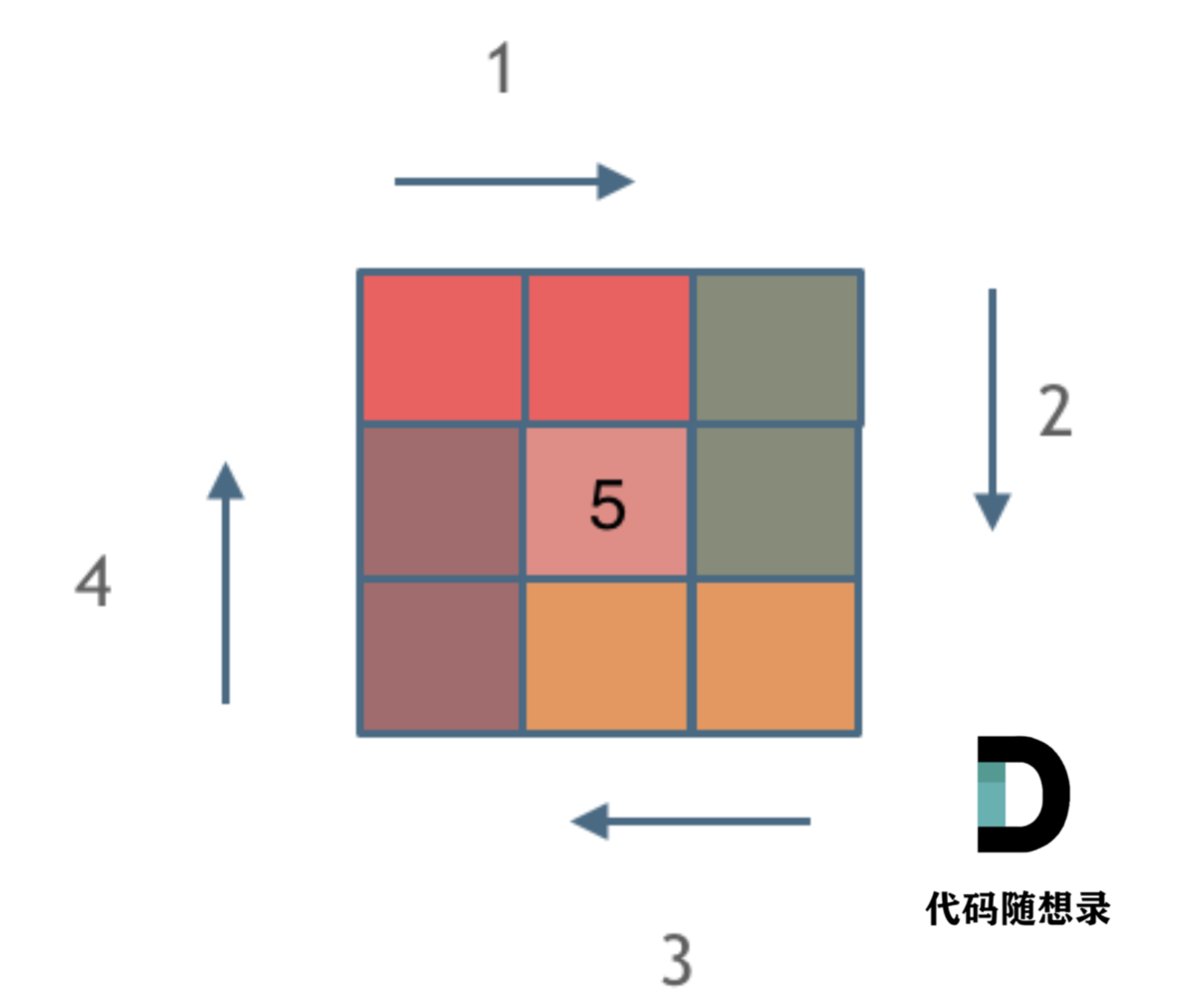
对每条边的处理保持一致，每条边均采用左闭右开统一处理，避免出现混乱，即循环不变量原则。
不变量：坚持相同的原则。在本题中就是坚持每条边左闭右开的原则，最右侧元素留作下一条边的起始元素进行处理。

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];
        int startX = 0, startY = 0; // 每圈起点
        int count = 1; // 用于填充的数
        int offset = 1;
        int loop = 1; // 记录循环次数
        int i, j; // j代表列,i代表行
        while (loop <= n/2) {
            // 顶部
            // 左闭右开，j不能取 n - offset
            for (j = startY; j < n - offset; j++) {
                matrix[startX][j] = count++;
            }
            // 右列
            // 左闭右开，i不能取 n - offset
            for (i = startX; i < n - offset; i++) {
                matrix[i][j] = count++;
            }
            // 底部
            // 左闭右开，j不能取startX
            for (; j > startX; j--) {
                matrix[i][j] = count++;
            }
            // 右列
            // 左闭右开，i不能取startY
            for (; i > startY; i--) {
                matrix[i][j] = count++;
            }

            startX++;
            startY++;
            offset++;
            loop++;
        } 

        // n为奇数
        if (n % 2 == 1) matrix[startX][startY] = count;

        return matrix;
    }
}

进阶
当n为奇数时，剩下最后矩阵中心元素未填充。
offset的意义：结束一圈填充后，下一圈填充的起始位置向后移，结束位置向前移。起始位置（startX, startY），结束位置（n - offset， n - offset）。

补充