论文阅读之PointGLR(Global-Local-Bidirectional Reasoning)
Global-Local Bidirectional Reasoning for Unsupervised Representation Learning of 3D Point Clouds
Global-Local Bidirectional Reasoning简称GLR,通过无监督学习的方式,不依赖于数据的标注来学习点云的特征表示。
文章的观点是监督学习方法强烈依赖于数据的标注信息,标注数据耗费人的劳动力,针对标注进行学习没有学习到点云本身内在的结构信息,限制了学到的模型的泛化能力。而目前的一些已有的无监督学习方法只能捕获点云低层次的结构信息,不能或者难以捕获高层次的语义特征。
这篇文章的灵感来源于生活中人们看到一个物体的一部分就能够知道该物体是什么,也即通过观察物体的局部就能得出全局。作者假设3D物体强大的特征表示建立于一个物体局部和全局间共享的且能与其他物体区分的属性,并提出从局部推断全局和从全局推断局部两个任务来学习点云的特征表示。
Local-to-Global Reasoning
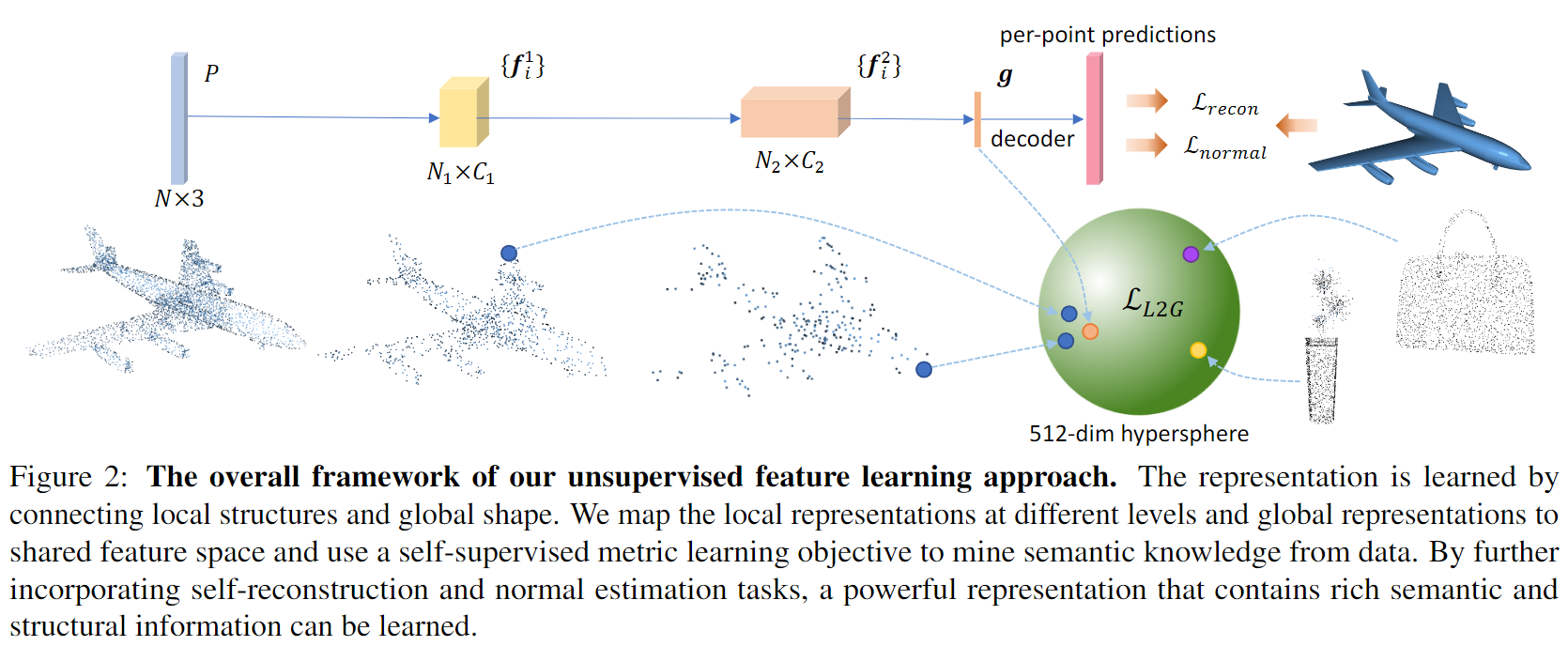
这篇文章建立在多级结构的网络基础之上,如PointNet++、RSCNN。这些方法通过降采样得到邻域的中心,利用球查询或KNN进行邻域内点的查找,并利用PointNet提取邻域点的全局特征,实现了类似卷积神经网络的局部特征提取以及多级结构增大感受野。基于这些网络结构,Local-to-Global Reasoning所作的就是想通过局部特征预测出全局特征,也就是希望通过网络中不同抽象层的局部特征向全局特征靠拢。
定义\(\textbf{f}^{l}_i\)为网络的第\(l\)层的第\(i\)个局部特征,\(g\)为网络提取的点云的全局特征。由于要让局部特征向同一个物体的全局特征靠近,可以将全局特征当作Ground Truth,将局部特征当作Prediction,由于每一层的局部特征维度不相同,且于全局特征的维度也不相同,因此提出使用多层感知机\(\phi^{l}\)用于对第\(l\)层的局部特征做维度提升,用\(\varphi\)用于对全局特征做维度提升,使得所有的局部特征和全局特征维度一致。
这个部分的损失函数定义如下:
上面定义的是某一个抽象层的某一个局部特征特征的损失,下面要计算所有抽象层的所有局部特征的损失:
其中\(\{\mathbf{g}_k, k=1, 2, ..., m\}\)是一个小批量数据的全局特征,\(m\)为小批量的样本数目,\(M\)为所有层的局部特征的数目综合。\(s=64\)是一个缩放因子,论文中说使用这个缩放因子会提升效果,但是原因没有给出。另外,其实公式2中的上面推导出下面这部分我自己没有推出来。
最终学到的特征,也就是用来作为点云的表示的特征是局部特征与全局特征的融合:
Global-to-Local Reasoning
在局部到全局的推断中,将全局特征作为Ground Truth,必须保证全局特征的质量,这样才能形成一个良性循环,即好的全局特征引导局部特征,好的局部特征推到全局特征。为了保证全局特征的质量,文章提出两个子任务:点云重构和法向量估计。
-
点云重构
点云重构使用得到的融合特征表示\(\mathbb{f}\)作为全局特征,并使用FlodingNet进行两次Floding Operation,得到重构的点云。重构的点云与原始点云之间的度量使用Chamer Distance:
\[\mathcal{L}_{recon}=\sum_{p\in P}\min_{x \in D\left(\mathbf{g}\right)}{||x-p||_{2}}+\sum_{x \in D\left(\mathbf{g}\right)}\min_{p\in P}{||x-p||_{2}} \] -
法向量估计
法向量估计通过将原始点云的xyz坐标和全局特征\(\mathbb{f}\)进行拼接并送入MLP中预测得到与点云点数相同的法向量数量,每个法向量是一个一维向量。法向量与点云原始法向量之间的度量使用下列损失:
\[\mathcal{L}_{normal}=1-\frac{1}{N}\sum_{i}\cos{\sigma\left(\left[p_i, \phi\left(\mathbf{g}\right)\right], p^{normal}_i\right)} \]
最终用于梯度下降最小化损失就是上面三个损失的和:
实验
简单地看一下分类效果的对比、跨数据集实验以及消融实验:
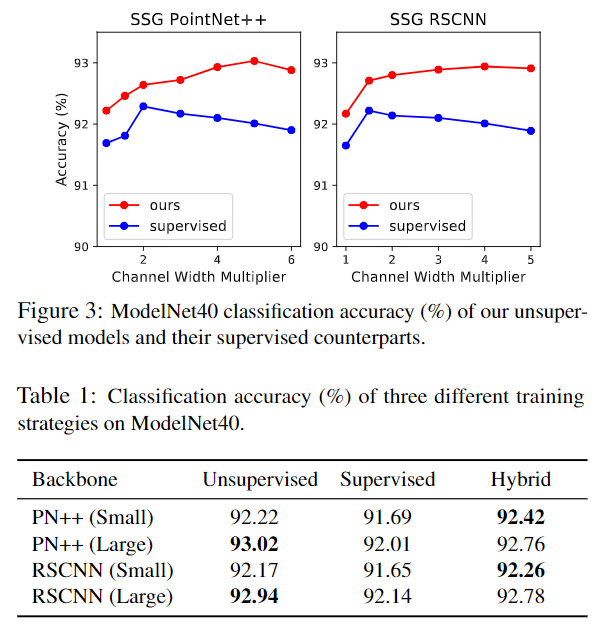
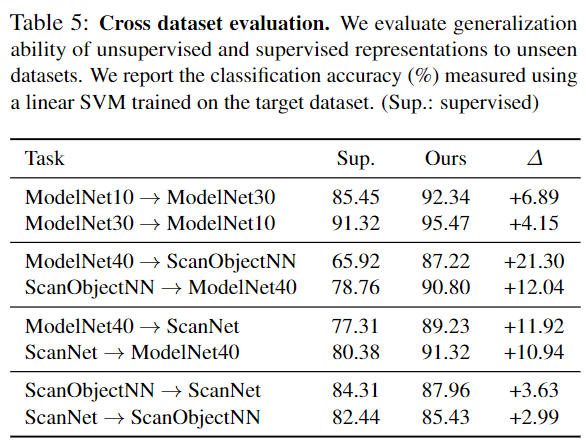

个人感受
其实这篇文章从观点到实现,逻辑性个人感觉不是很强。为什么用重构和法向量估计这两个任务就能保证全局特征的质量?论文前面所讲的一些概念在我看来其实比较抽象,跟实现的好像并没有很大的联系。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号