论文阅读之PointNet++

PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

PointNet++是PointNet的延续，或者说是PointNet的改进。PointNet使用shared mlp单独地处理每个点并使用max pooling进行特征的聚合，能够处理点云的无序性。但是PointNet没有提取点云的局部特征，这里的局部特征不是指一个点的特征，而是一个邻域。在卷积神经网络处理图像时，通过使用一定大小的卷积核对图像进行卷积操作，而卷积核的大小对应的图像区域就是一个局部区域，通过多级结构，不断增加感受野。因此PointNet++尝试提取点云的局部特征，并通过多级网络结构，产生高层次的特征。

那么问题来了，点云数据不像图像数据，图像数据是一个规则的网格结构，而点云是一个不规则的点集，具有无序性。因此，如何对点云进行局部区域的划分，以及如何对局部区域进行特征提取就是本文的重点。

邻域划分

对于如何划分邻域，本文给出的方案是对原始点云进行降采样得出一系列的点，以这些点为中心，以固定大小的半径定义一个球邻域，在球领域内的点即为一个局部区域。给定一个含有 \(N\) 个点的点云，邻域划分分为以下两步：

1. 降采样：降采样使用FPS算法，FPS即最远点采样，第一个点从点云中随机选取，第二个点选剩下的点中距离第一个点最远的点，第三个点选剩下的点云中距离前两个点最近的点，依此类推。经过降采样，得到 \(N^{'}\) 个点，这\(N^{'}\)个点就是局部邻域的中心。
2. 球查询：对于降采样得到的\(N^{'}\)点的每个点，我们把它们当作球心，即有\(N^{'}\)个球心，然后给定一个半径\(r\)，定义出\(N^{'}\)个球。每个球中所包含的点即为该邻域内的所有点。在实现时，通常会给定一个上限值\(k\)。当然，这里需要注意的是，每个球邻域找出来之后，需要用球邻域的点减去中心点，转换成局部坐标。

假设点云中每个点的坐标为\(d\)维(\(d = 3\))，其额外的特征为\(C\)维(法向量、RGB等)。那么经过一次邻域划分，由原来的\(N \times \left(d + C\right)\)得到\(N^{'} \times \left(d + C\right)\)。

邻域特征提取

经过邻域划分得到每个球邻域内的点云仍然是无序的，为了提取一个邻域的特征，自然而然想到的是PointNet。对于\(N^{'}\)个邻域，使用同一个PointNet进行特征提取，得到\(N^{'} \times (d + C^{'})\)。\(d\)代表邻域中新的坐标的维度，\(C^{'}\)则代表了通过shared mlp将\(d+C\)维度提升到\(C^{'}\)。

以上两个步骤组成了网络中的一层特征提取。下面给出网络整体结构：

网络结构

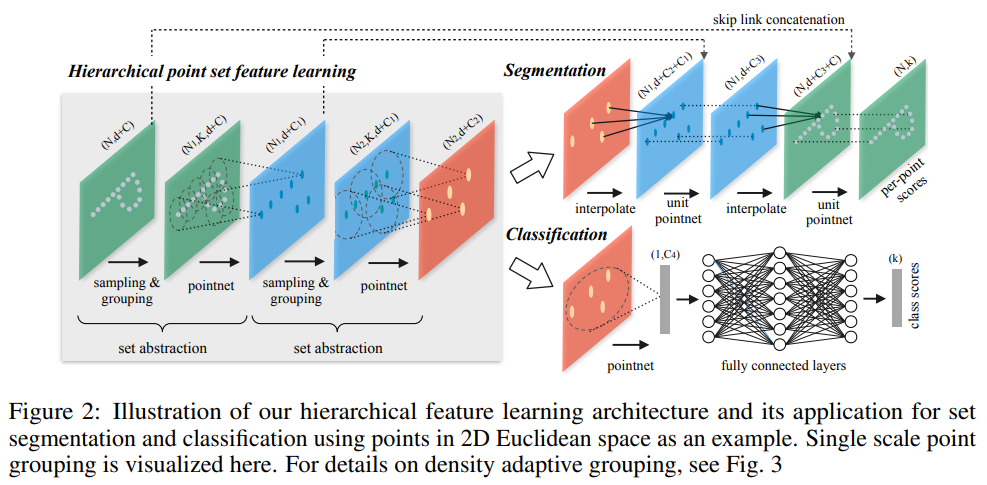
网络中，一个set abstraction层包括FPS降采样、球查询以及使用PointNet对邻域特征进行提取。每一层在上一层的结果基础之上，再进行FPS降采样、球查询、PointNet特征提取，每经过一个set abstraction点的数量都会减少一次。

对于分类任务而言，在最后需要进行一个全局的set abstraction，也就是以\(\left(0, 0, 0\right)\)为中心，所有剩下的点为一个球邻域，使用一个PointNet进行全局特征提取，得到一个\(1 \times C_4\)的全局特征，然后送入MLP中进行分类。

而对于分割任务而言，由于每次set abstraction操作使得点的数目变少了，最后的分割任务无法进行。因此需要将点数恢复到原来的点云数目，因此需要进行插值操作。假设第\(l-1\)层有\(N^{l-1}\)个点，即\(N^{l-1} \times \left(d + C^{l - 1}\right)\)，经过set abstraction之后得到第\(l\)层有\(N^{l}\)个点， 即\(N^{l} \times (d + C^{l})\)，且\(N^{l} < N^{l - 1}\)。插值的具体操作就是将第\(l-1\)层的每个点作为插值后的点，其特征需要在第\(l\)层寻找最近的\(k\)个点(\(k=3\))的特征的一个加权平均，而权重就是点的距离的\(p\)次方的倒数(\(p=2\))。

\[f^{\left(j\right)}\left(x\right)=\sum_{i=1}^{k}\frac{w_i\left(x\right)f^{\left(j\right)}_i}{\sum_{i=1}^{k}w_i\left(x\right)} \]

\[w_i\left(x\right)=\frac{1}{d\left(x, x_i\right)^p}, j=1,...,C \]

点云密度的鲁棒性问题

点云在每个区域的点的密度是不一样的。有的地方稀疏，有的地方密集。因此对于球查询时的半径选择十分重要。类比到卷积神经网络，卷积核的大小通常选取较小的卷积核如3x3或5x5，但是在点云中，小的邻域半径肯能因为稀疏性的问题使得领域内只有中心点一个点，因此局部邻域太小，根本不足以代表局部。

为了解决该问题，论文中给出了两种方案：MSG(multi-scale grouping)和MRG(Multi-resolution grouping)。

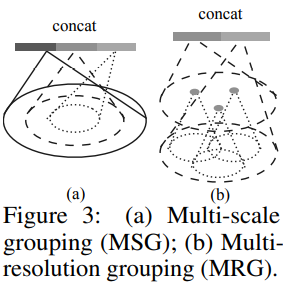
1. MSG

   MSG在每次球查询时使用不同大小的半径，这就是所谓的多尺度multi-scale。对于每个尺度，都对应一个PointNet，也就是说有几个尺度，就有几个不同的PointNet。而在SSG中，只给定了一个尺度大小的半径，因此对所有的邻域只是用一个PointNet进行特征提取。

   多尺度的特征提取后，每个尺度得到的特征的channel数是不一样的，但是特征数量是一样的，MSG直接将这些不同尺度的特征按channel进行拼接，得到了融合了多尺度的局部特征。

   MSG结合了对点云的输入数据的dropout，也就是说，对输入的点云的每个点的坐标以一定的比例将其设为全0。这个比例在\(\left[0, p\right]\)之间随机取得，\(p \leq 1\)。文中说到为了确保点云不被全部dropout，因此设置\(p=0.95\)。

2. MRG

   MSG的有一个明显的缺点，就是计算量大。在低层时，FPS降采样得到的点是很多的，对不同尺度的划分用不同的PointNet，计算量是庞大的。因此提供另外一种选择，减少了计算量，同时一定程度上保证了鲁棒性。MRG的思想就是，一方面，通过set abstraction提取特征，另一方面，直接对局部区域的点用一个PointNet进行处理，两个得到的特征进行拼接。

实验

实验部分，我们重点看看PointNet++与PointNet的对比以及消融实验。

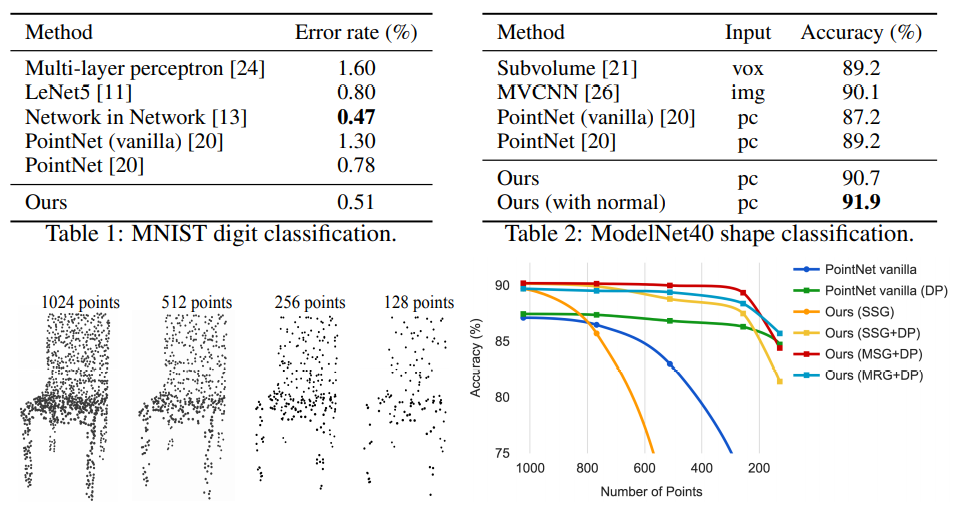
对于ModelNet40数据集的分类而言，实现了最好的性能，比PointNet++要好。对于点的稀疏性鲁棒性实验中，MSG的鲁棒性是最好的，同时可以看到，通过对输入点云进行dropout操作，提升了PointNet的鲁棒性。

其他

• 论文地址：PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

• 代码地址：Tensorflow、PyTorch