主席树学习笔记
其实主席树我在 10000 年前就会了但这个知识点题单顺序非常靠后导致现在才写(
1 算法介绍
主席树是可持久化权值线段树的别称,但这个权不权值的已经没有人强调了,我也会混淆主席树和普通权值线段树的概念,毕竟主席树字少嘛🤔。
1.1 单点修改
先讲可持久化维护单点修改区间查询。
可持久化:指能够维护历史版本。
不难想到一些蠢做法,比如每次操作先把整颗线段树复制一遍再修改,复杂度堪称神人🤩。
考虑优化,注意到一次单点修改只会改 \(\log_n\) 个节点的值,其他的点直接抄上一个版本即可。
于是我们对于每一个版本开一个新线段树根,不变的儿子直接指向上个版本的对应点,否则新建一个,就像下面这张我拷的示意图:
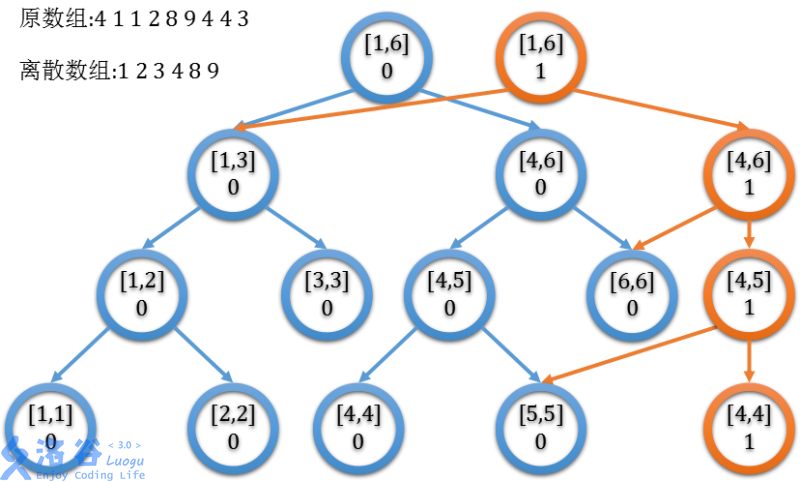
嗯,没了,很简单吧。
优美模版,以插入一个序列 a 为例
#include<bits/stdc++.h>
#define int long long//恶臭习惯
using namespace std;
namespace kong{bool st;}
namespace zhu{
int a[200200],n,m,b[200200],w;
int cnt,rt[200200];
struct MurasameCute{
int l,r,ls,rs,sum;
}tr[30000000];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define mid ((l(id)+r(id))>>1)
#define up sm(id)=sm(ls(id))+sm(rs(id))
void crt(int &id,int l,int r,int sum=0){//新建节点
id=++cnt;
l(id)=l,r(id)=r,sm(id)=sum;
}
void copy(int &to,int fr){//让 to 变为和 fr 完全一样的一个新节点
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
crt(id,l,r,0);
if(l==r) return;
build(ls(id),l,mid);
build(rs(id),mid+1,r);
}
void insert(int id,int x,int y){
if(l(id)==r(id)){
sm(id)+=y;
return;
}
if(x<=mid){
copy(ls(id),ls(id));//先复制一遍再改
insert(ls(id),x,y);
}
else{
copy(rs(id),rs(id));
insert(rs(id),x,y);
}
up;
}
string main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
copy(rt[i],rt[i-1]);//建树也要先复制之前的
insert(rt[i],a[i],1);
}
return "Ciallo~(∠> ω< )⌒☆";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB()<<'\n';
return 0;
}
1.2 区间修改
照着普通的标记永久化去写就好了,直接看注释吧。
void insert(int id,int l,int r,int y){
sm(id)+=1ll*(min(r,r(id))-max(l,l(id))+1)*y;//遍历到的直接改
if(l(id)>=l&&r(id)<=r){//为了保证复杂度这里必须 return 所以打上标记
lz(id)+=y;
return;
}
if(l<=mid){
copy(ls(id),ls(id));
insert(ls(id),l,r,y);
}
if(r>mid){
copy(rs(id),rs(id));
insert(rs(id),l,r,y);
}
}
long long query(int id,int l,int r,int y){//y是标记的和
if(l(id)>=l&&r(id)<=r){
return sm(id)+1ll*(r(id)-l(id)+1)*y;//加上标记的贡献
}
long long ans=0;
if(l<=mid){
ans+=query(ls(id),l,r,y+lz(id));
}
if(r>mid){
ans+=query(rs(id),l,r,y+lz(id));
}
return ans;
}
2 算法应用
2.1 求区间第 k 大
相当典的应用,第 \(k\) 大和主席树简直能有映射关系。
丛雨可爱。
先想如何求 \([1,l]\) 的第 \(k\) 大。
我们考虑构建权值主席树依次插入 \(a\) 的每一位,这样就把下标转换为了版本,然后直接查 \(l\) 版本的第 \(k\) 大就好了,权值线段树求全局第 \(k\) 大应该连丛雨都会所以不再赘述。
那么求 \([l,r]\) 的第 \(k\) 大也并非难事,注意到用 \([1,r]\) 的信息减去 \([1,l-1]\) 的信息就是 \([l,r]\) 的信息,同时维护这两个版本上跳到的位置然后调用时做差即可。
int kth(int idl,int idr,int k){
if(l(idl)==r(idl)){//找到了
return l(idl);
}
int x=sm(ls(idr))-sm(ls(idl));//做差求 [l,r] 的信息
if(x>=k){//经典线段树二分
return kth(ls(idl),ls(idr),k);
}
else{
return kth(rs(idl),rs(idr),k-x);
}
}
2.2 区间数颜色
可爱丛雨,但自觉强制在线一手。
发现这题强制的话在线莫队就爆炸了😭。
考虑一个点有贡献当且仅当:
- 它的下标在区间内
- 它的颜色上次出现时不在区间内
那么我们按 2 建权值线段树,以 1 为版本号就做完了。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
int a[500500],n,m,pre[500500],val[500500];
int cnt=0,rt[500500];
struct Murasame{
int l,r,ls,rs,sum;
}tr[500500*32];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define ls tr[id].ls
#define rs tr[id].rs
#define sm(x) tr[x].sum
#define mid ((l(id)+r(id))>>1)
#define up sm(id)=sm(ls)+sm(rs)
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
id=++cnt;
l(id)=l,r(id)=r,sm(id)=0;
if(l==r) return;
build(ls,l,mid);
build(rs,mid+1,r);
}
void insert(int id,int x,int y){
if(l(id)==r(id)){
sm(id)+=y;
return;
}
if(x<=mid){
copy(ls,ls);
insert(ls,x,y);
}
else{
copy(rs,rs);
insert(rs,x,y);
}
up;
}
int que(int id,int l,int r){
if(l(id)>=l&&r(id)<=r){
return sm(id);
}
int ans=0;
if(l<=mid){
ans+=que(ls,l,r);
}
if(r>mid){
ans+=que(rs,l,r);
}
return ans;
}
string main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
val[i]=pre[a[i]];
pre[a[i]]=i;
}
build(rt[0],0,n);
for(int i=1;i<=n;i++){
copy(rt[i],rt[i-1]);
insert(rt[i],val[i],1);
}
int ans=0;
while(m--){
int l,r;
cin>>l>>r;
l=(l+ans)%n+1;
r=(r+ans)%n+1;
if(l>r) swap(l,r);
ans=(que(rt[r],0,l-1)-que(rt[l-1],0,l-1));
cout<<ans<<'\n';
}
return "疯狂的色!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB()<<'\n';
return 0;
}
2.3 小结
你大体可以感受到主席树的版本号不一定要是版本号🤔,做题时转化成维护矩阵信息就能主席树了。
3 例题
3.1 [SDOI2013] 森林
题意简述
含有 \(n\) 个带权点的森林,初始有 \(m\) 条边,强制在线要求实现 \(q\) 次操作:
- 查询 \(x\) 到 \(y\) 的第 \(k\) 小权值,保证路径存在。
- 连接 \(x,y\),保证连接后图仍是森林。
\(n,m,q\le 8\times10^4\)。
题解
第 \(k\) 小主席树维护一下到根的序列查询的时候做经典荣斥 f(u)+f(v)-f(lca)-f(father[lca]),合并时启发式每次把小的那颗的倍增数组和主席树暴力重构,这是 \(n\log^2_n\) 的,可以通过。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
int Ciallo,n,m,q,root[80800],fa[80800*10][30],a[80800],siz[80800],head[80800],tot,dep[80800];
int b[80800],num;
struct{
int to,nxt;
}e[80800*2];
void pan(int x,int len,int line){
if(x>=len){
cerr<<x<<" "<<len<<' '<<line<<"越界!\n";
exit(114514);
}
if(x<0){
cerr<<line<<"越界!\n";
exit(114514);
}
}
void add(int u,int v){
tot++;
e[tot].to=v;
e[tot].nxt=head[u];
pan(u,sizeof(head)/4,26);
head[u]=tot;
}
int cnt=0,rt[80800];
struct Murasame{
int ls,rs,sum;
}tr[80000*600];
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define up sm(id)=sm(ls(id))+sm(rs(id))
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
id=++cnt;
sm(id)=0;
if(l==r) return;
int mid=(l+r)>>1;
build(ls(id),l,mid);
build(rs(id),mid+1,r);
}
void insert(int id,int x,int y,int l,int r){
if(l==r){
sm(id)+=y;
return;
}
int mid=(l+r)>>1;
if(x<=mid){
copy(ls(id),ls(id));
insert(ls(id),x,y,l,mid);
}
else{
copy(rs(id),rs(id));
insert(rs(id),x,y,mid+1,r);
}
up;
// cout<<"AfterInsert:"<<id<<' '<<sm(id)<<'\n';
}
int kth(int idu,int idv,int idlc,int idfalc,int k,int l,int r,int flag=0){
assert(idu<80000*600);
assert(idv<80000*600);
assert(idlc<80000*600);
assert(idfalc<80000*600);
// cout<<"NowWeHave"<<cnt<<"Points!\n";
// cout<<"IduOn"<<idu<<"thPoint.\n";
// cout<<"IdvOn"<<idv<<"thPoint.\n";
// cout<<"IdlcOn"<<idlc<<"thPoint.\n";
// cout<<"IdfalcOn"<<idfalc<<"thPoint.\n";
// cout<<"querying...\n";
if(l==r){
// if(flag)cerr<<"findat"<<idu<<'\n';
return l;
}
int x=sm(ls(idu))+sm(ls(idv))-sm(ls(idlc))-sm(ls(idfalc)),mid=(l+r)>>1;
// if(flag){
// cerr<<l<<' '<<r<<' '<<x<<" "<<k<<'\n';
// }
if(x>=k){
return kth(ls(idu),ls(idv),ls(idlc),ls(idfalc),k,l,mid,flag);
}
else{
return kth(rs(idu),rs(idv),rs(idlc),rs(idfalc),k-x,mid+1,r,flag);
}
}
int lca(int u,int v){
pan(u,sizeof(dep)/4,102);
pan(v,sizeof(dep)/4,102);
// cout<<"fucking...\n";
if(dep[u]<dep[v]) swap(u,v);
for(int i=16;i>=0;i--){
if(dep[fa[u][i]]>=dep[v]){
u=fa[u][i];
}
}
if(u==v) return u;
for(int i=16;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
u=fa[u][i];
v=fa[v][i];
}
}
return fa[u][0];
}
int searchingtimes;
void dfs(int x,int f,int RT){
searchingtimes++;
pan(RT,sizeof(siz)/4,123);
siz[RT]++;
pan(x,sizeof(root)/4,125);
root[x]=RT;
fa[x][0]=f;
pan(x,sizeof(dep)/4,128);
dep[x]=dep[f]+1;
for(int i=1;i<=16;i++){
fa[x][i]=fa[fa[x][i-1]][i-1];
}
pan(x,sizeof(rt)/4,133);
pan(f,sizeof(rt)/4,133);
copy(rt[x],rt[f]);
pan(x,sizeof(a)/4,136);
insert(rt[x],a[x],1,1,n);
// if(x==70449){
// cerr<<"Ciallo!"<<kth(rt[x],rt[x],rt[x],rt[f],1,1,n,1)<<' '<<a[x]<<' '<<b[a[x]]<<'\n';
// }
pan(x,sizeof(head)/4,138);
for(int i=head[x];i;i=e[i].nxt){
assert(i<80800*2);
int v=e[i].to;
if(v==f) continue;
dfs(v,x,RT);
}
}
string main(){
// freopen("P3302_7.in","r",stdin);
// freopen("my.txt","w",stdout);
cin>>Ciallo>>n>>m>>q;
for(int i=1;i<=n;i++){
pan(i,sizeof(a)/4,151);
cin>>a[i];
pan(num+1,sizeof(b)/4,153);
b[++num]=a[i];
}
sort(b+1,b+num+1);
num=unique(b+1,b+num+1)-b-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(b+1,b+1+num,a[i])-b;
}
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
build(rt[0],1,n);
for(int i=1;i<=n;i++){
if(!fa[i][0]){
dfs(i,0,i);
}
}
int ans=0,quecnt=0;
for(int i=1;i<=q;i++){
char opt;
int x,y,k;
cin>>opt>>x>>y;
x^=ans,y^=ans;
if(opt=='Q'){
cin>>k;
k^=ans;
// if(x>n){
// cerr<<quecnt<<" "<<ans<<'\n';
// }
quecnt++;
assert(x<=n),assert(y<=n);
int lc=lca(x,y);
pan(x,sizeof(rt)/4,183);
pan(y,sizeof(rt)/4,184);
pan(lc,sizeof(rt)/4,185);
pan(fa[lc][0],sizeof(rt)/4,186);
if(quecnt==443){
// cerr<<x<<" "<<y<<" "<<lc<<" "<<k<<" "<<fa[lc][0]<<'\n';
ans=b[kth(rt[x],rt[y],rt[lc],rt[fa[lc][0]],k,1,n,1)];
}
else{
// assert(rt[x]<=cnt);
ans=b[kth(rt[x],rt[y],rt[lc],rt[fa[lc][0]],k,1,n)];
}
cout<<ans<<'\n';
}
else{
pan(x,sizeof(root)/4,192);
pan(y,sizeof(root)/4,193);
pan(root[x],sizeof(siz)/4,194);
pan(root[y],sizeof(siz)/4,195);
if(siz[root[x]]>siz[root[y]]) swap(x,y);
add(x,y);add(y,x);
for(int i=0;i<=16;i++){
fa[x][i]=0;
}
int sum=siz[root[x]]+siz[root[y]];
dfs(x,y,root[y]);
assert(siz[root[y]]==sum);
}
}
return "Senli!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB();
return 0;
}
/*
1
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3
Q 3 5 1
Q 10 0 0
L 5 4
L 3 2
L 0 7
Q 9 2 5
Q 6 1 6
*/
3.2 [AHOI2017/HNOI2017] 影魔
题意简述
给出一个长度 \(n\) 的排列 \(a\),有 \(q\) 组询问,每次给出一个区间。
- 若区间内存在 \(i,j~(i<j)\) 使得不存在 \(a_k>\min(a_i,a_j)~(i<k<j)\) 则将贡献加 \(p_1\)。
- 若区间内存在 \(i,j~(i<j)\),\((i,j)\) 中最大值 \(a_k\) 满足 \(\max(a_i,a_j)>a_k>\min(a_i,a_j)~(i<k<j)\) 则将贡献加 \(p_2\)。

\(n,m\le2\times10^6,p_1,p_2\le10^3\)。
题解
有点难度的题目。
首先这个贡献式简直不是人能看的😡,转化一手发现当 \(a_i\) 和 \(a_j\) 中有一个是最大值,则另一个是次大值就将贡献加 \(p_1\),否则增加 \(p_2\),这个自己手膜一下应该不难发现。
都必须有一个点是最大值了还不单调栈一手?预处理出 \(i\) 左边第一个大于 \(a_i\) 的位置 \(l_i\) 和右边第一个大于 \(a_i\) 的位置 \(r_i\),那么对于每一个 \(i\),有:
- \((i,i+1)\) 有贡献 \(p_1\)。
- \((l_i,r_i)\) 有贡献 \(p_1\)。
- \((l_i,x\in(i+1,r_i-1))\) 有贡献 \(p_2\)。
- \((x\in(l_i+1,i-1),r_i)\) 有贡献 \(p_2\)。
发现这长得很像坐标有没有,而且我们查询的时候需要让左右端点都在区间里就相当于一个矩阵查。
那么主席树怎么维护呢,容易想到将第一个坐标作为版本号,第二个坐标作为修改,写一个区间修改区间查询可以容易维护前三种情况,但最后一种怎么办呢🤨?
发现其实我们并不需要保证第一个个坐标小于第二个坐标,于是将最后一种的前后项交换即可维护🎉。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
int n,m,p1,p2,a[200200],L[200200],R[200200];
struct CuteMurasame{
int l,r,v;
};
stack<int> st;
vector<CuteMurasame> V[200200];
int cnt,rt[200200];
struct MurasameCute{
int l,r,ls,rs;
long long sum,lazy;
}tr[200000*80];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define lz(x) tr[x].lazy
#define mid ((l(id)+r(id))>>1)
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
id=++cnt;
l(id)=l,r(id)=r;
if(l==r) return;
build(ls(id),l,mid);
build(rs(id),mid+1,r);
}
void insert(int id,int l,int r,int y){
sm(id)+=1ll*(min(r,r(id))-max(l,l(id))+1)*y;
if(l(id)>=l&&r(id)<=r){
lz(id)+=y;
return;
}
if(l<=mid){
copy(ls(id),ls(id));
insert(ls(id),l,r,y);
}
if(r>mid){
copy(rs(id),rs(id));
insert(rs(id),l,r,y);
}
}
long long query(int id,int l,int r,int y){
if(l(id)>=l&&r(id)<=r){
return sm(id)+1ll*(r(id)-l(id)+1)*y;
}
long long ans=0;
if(l<=mid){
ans+=query(ls(id),l,r,y+lz(id));
}
if(r>mid){
ans+=query(rs(id),l,r,y+lz(id));
}
return ans;
}
string main(){
cin>>n>>m>>p1>>p2;
for(int i=1;i<=n;i++){
cin>>a[i];
R[i]=n+1;
}
for(int i=1;i<=n;i++){
while(!st.empty()&&a[st.top()]<a[i]){
R[st.top()]=i;
st.pop();
}
if(!st.empty()) L[i]=st.top();
st.push(i);
}
for(int i=1;i<=n;i++){
// cout<<L[i]<<" "<<R[i]<<'\n';
V[L[i]].push_back({i+1,R[i]-1,p2});
V[R[i]].push_back({L[i]+1,i-1,p2});
V[L[i]].push_back({R[i],R[i],p1});
V[i].push_back({i+1,i+1,p1});
}
build(rt[0],0,n+1);
for(int i=1;i<=n;i++){
copy(rt[i],rt[i-1]);
for(auto j:V[i]){
// cout<<i<<" "<<j.l<<" "<<j.r<<" "<<j.v<<"\n";
insert(rt[i],j.l,j.r,j.v);
}
}
for(int i=1;i<=m;i++){
int l,r;
cin>>l>>r;
cout<<query(rt[r],l,r,0)-query(rt[l-1],l,r,0)<<'\n';
}
return "淫魔!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB()<<'\n';
return 0;
}
3.3 [bzoj4026] dC Loves Number Theory
题意简述
给出一个长为 \(n\) 的序列 \(a\),\(q\) 次强制在线询问 \(\varphi (\prod\limits_{i=l}^ra_i)\)。
\(n\le 5\times 10^4,q\le 10^5,a_i\le 10^6\)。
题解
板题。
As we all know,\(\varphi(n)=n\prod(1-\frac{1}{p})\),其中 \(p\) 为质因子。
这个式子中的 \(n\) 就是区间积,前缀和即可,后面的质因子就是区间内质因子的并集。
考虑怎么去重,2.2 讲区间数颜色了吧,带个权套用过来,值域这么小直接拆质因子往树上丢就做完了。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace kong{bool st;}
namespace zhu{
const int mod=1e6+777;
int n,q,a[50500],lst[1001000],sum[50500];
int rt[50500],cnt;
int qpow(int x,int y){
int ans=1;
while(y){
if(y&1) ans=ans*x%mod;
x=x*x%mod;
y>>=1;
}
return ans;
}
int inv(int x){
return qpow(x,mod-2);
}
int calc(int x){
return (1-inv(x)+mod)%mod;
}
struct MurasameCute{
int l,r,ls,rs,sum;
}tr[50500*128];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define mid ((l(id)+r(id))>>1)
#define up sm(id)=sm(ls(id))*sm(rs(id))%mod;
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
id=++cnt;
sm(id)=1;
l(id)=l,r(id)=r;
if(l==r) return;
build(ls(id),l,mid);
build(rs(id),mid+1,r);
}
void insert(int id,int x,int y){
if(l(id)==r(id)){
// cout<<id<<"乘了"<<y<<"!\n";
sm(id)=sm(id)*y%mod;
return;
}
if(x<=mid){
copy(ls(id),ls(id));
insert(ls(id),x,y);
}
else{
copy(rs(id),rs(id));
insert(rs(id),x,y);
}
// cout<<id<<"乘了"<<y<<"!\n";
up;
}
int query(int idl,int idr,int l,int r){
if(l(idl)>=l&&r(idl)<=r){
return sm(idr)*inv(sm(idl))%mod;
}
int md=((l(idl)+r(idl))>>1),ans=1;
if(l<=md){
ans=ans*query(ls(idl),ls(idr),l,r)%mod;
}
if(r>md){
ans=ans*query(rs(idl),rs(idr),l,r)%mod;
}
return ans;
}
string main(){
cin>>n>>q;
sum[0]=1;
build(rt[0],0,n);
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]*a[i]%mod;
int t=a[i];
copy(rt[i],rt[i-1]);
for(int j=2;j<=sqrt(a[i]);j++){
if(t%j==0){
// cout<<"版本 "<<i<<"在"<<lst[j]<<"乘了calc"<<j<<'\n';
insert(rt[i],lst[j],calc(j));
while(t%j==0) t/=j;
lst[j]=i;
}
}
if(t!=1){
// cout<<"版本 "<<i<<"在"<<lst[t]<<"乘了calc"<<t<<'\n';
insert(rt[i],lst[t],calc(t));
lst[t]=i;
}
}
// cout<<100*calc(2)%mod*calc(5)%mod<<'\n';
int ans=0;
for(int i=1;i<=q;i++){
int l,r;
cin>>l>>r;
l^=ans,r^=ans;
// cout<<l<<"到"<<r<<"的积为"<<sum[r]*inv(sum[l-1])%mod<<",假人们我算的对吗?\n";
// cout<<"查询版本"<<l<<"到版本"<<r<<"中0到"<<l-1<<"的答案\n";
ans=query(rt[l-1],rt[r],0,l-1)*sum[r]%mod*inv(sum[l-1])%mod;
cout<<ans<<"\n";
}
return "Theory!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB();
return 0;
}
/*
5 1
3 7 10 10 5
3 4
*/
3.4 [国家集训队]middle
题意简述
给出一个长为 \(n\) 的序列 \(a\),\(q\) 次强制在线询问左端点在 \((l_1,r_1)\),右端点在 \((l_2,r_2)\) 的区间中位数最大值。
当序列长度 \(p\) 为偶数时记中位数为第 \(\lceil \frac{p}{2}\rceil\) 小的元素。
\(n\le 2\times10^4,q\le2.5\times10^4,a_i\le10^9\)。
题解
有点难写的板题。
看到中位数极值那我奶奶都会去二分答案然后 \(<mid\) 的改成 \(-1\),\(\ge mid\) 的改成 \(1\) 的🤓。
那么问题就转化为最大的 \(mid\) 使得存在合法区间的元素和 \(\ge 0\),但这仍不好维护。
发现预处理出所有 \(mid\) 的前缀和后可以通过线段树 \(\log_n\) 查询,但预处理所花费的时间(\(O(n^2\log_n)\) 近一分钟)简直能让我攻略一次丛雨😩,\(n\) 颗线段树的空间占用(\(O(4n^2)\) 大于 1GB)更是能存下整个丛雨线调用的图片音频文字😱。
但是能救,发现枚举 \(mid\) 的话变化量和是 \(n\)(一个位置最多变一次)。
诶呀我的天哪刚刚这一段讲述简直就是最开始的引言,直接主席树维护前缀和就好了🥳,注意原数组的单点修改对应到前缀和数组就是后缀修改。
需要维护区间最大区间最小区间加,写出来宛如大粪😨。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
int n,a[20200],b[20200],tot,q,murasame[5];
int rt[20200],cnt;
vector<int> p[20200];
struct MurasameCute{
int l,r,ls,rs,min,max,lazy;
}tr[20200*128];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define mn(x) tr[x].min
#define mx(x) tr[x].max
#define lz(x) tr[x].lazy
#define mid ((l(id)+r(id))>>1)
#define up mn(id)=min(mn(ls(id))+lz(id),mn(rs(id))+lz(id)),mx(id)=max(mx(ls(id))+lz(id),mx(rs(id))+lz(id))
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void build(int &id,int l,int r){
id=++cnt;
l(id)=l,r(id)=r;
if(l==r){
mn(id)=mx(id)=-l;
return;
}
build(ls(id),l,mid);
build(rs(id),mid+1,r);
up;
}
void insert(int id,int l,int r,int y){
if(l(id)>=l&&r(id)<=r){
// cout<<"added"<<l(id)<<" "<<r(id)<<'\n';
mn(id)+=y,mx(id)+=y,lz(id)+=y;
return;
}
if(l<=mid){
copy(ls(id),ls(id));
insert(ls(id),l,r,y);
}
if(r>mid){
copy(rs(id),rs(id));
insert(rs(id),l,r,y);
}
up;
// cout<<l(id)<<" "<<r(id)<<" "<<l<<" "<<r<<" "<<mx(id)<<'\n';
}
int qmin(int id,int l,int r,int y){
if(l(id)>=l&&r(id)<=r){
return mn(id)+y;
}
int ans=1e9;
if(l<=mid){
ans=min(ans,qmin(ls(id),l,r,y+lz(id)));
}
if(r>mid){
ans=min(ans,qmin(rs(id),l,r,y+lz(id)));
}
return ans;
}
int qmax(int id,int l,int r,int y,int flag=0){
// if(flag) cout<<"查询max当前信息:"<<mx(id)<<" "<<l(id)<<" "<<r(id)<<" "<<l<<" "<<r<<" "<<y<<'\n';
if(l(id)>=l&&r(id)<=r){
return mx(id)+y;
}
int ans=-1e9;
if(l<=mid){
ans=max(ans,qmax(ls(id),l,r,y+lz(id),flag));
}
if(r>mid){
ans=max(ans,qmax(rs(id),l,r,y+lz(id),flag));
}
return ans;
}
#undef mid
string main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[++tot]=a[i];
}
sort(b+1,b+1+tot);
tot=unique(b+1,b+1+tot)-b-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
p[a[i]].push_back(i);
}
build(rt[tot+1],0,n);
for(int i=tot;i>=1;i--){
copy(rt[i],rt[i+1]);
// cout<<"-----------------\n";
for(auto x:p[i]){
insert(rt[i],x,n,2);
}
}
// cout<<"离散化后数组:\n";
// for(int i=1;i<=n;i++){
// cout<<a[i]<<' ';
// }
// cout<<'\n';
// for(int i=1;i<=tot+1;i++){
// cout<<"钦定中位数为"<<i<<"时:\n";
// int lst=0;
// for(int j=0;j<=n;j++){
// int q=qmax(rt[i],j,j,0);
// cout<<q-lst<<' ';
// lst=q;
// }
// cout<<'\n';
// }
cin>>q;
int ans=0;
while(q--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
murasame[1]=(l1+ans)%n+1,murasame[2]=(r1+ans)%n+1;
murasame[3]=(l2+ans)%n+1,murasame[4]=(r2+ans)%n+1;
sort(murasame+1,murasame+5);
l1=murasame[1],r1=murasame[2];
l2=murasame[3],r2=murasame[4];
// cout<<l1<<" "<<r1<<' '<<l2<<' '<<r2<<'\n';
int l=1,r=tot;
while(l<=r){
int mid=(l+r)>>1;
// cout<<"钦定中位数为"<<mid<<"时,右最大为"<<qmax(rt[mid],l2,r2,0,1)<<"左最小为"<<qmin(rt[mid],l1-1,r1-1,0)<<'\n';
if(qmax(rt[mid],l2,r2,0)-qmin(rt[mid],l1-1,r1-1,0)>=0){
l=mid+1;
}
else{
r=mid-1;
}
}
ans=b[l-1];
cout<<ans<<'\n';
}
return "middle!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB();
return 0;
}
/*
5
7 3 2 1 4
1
0 4 2 1
*/
3.5 [FJOI2016] 神秘数
题意简述
给出一个长为 \(n\) 的序列 \(a\),\(q\) 次询问区间丛雨数。
一个可重复集 \(S\) 的丛雨数定义为最小的不能被 \(S\) 的子集的和表示的正整数。
\(n,m\le10^5,\sum a\le 10^9\)。
题解
以下称丛雨数减一为“将臣数”。
首先这个丛雨数我看着相当眼熟,好像有一个结论是集合中比丛雨数小的数加起来一定会小于丛雨数,咋证来着🤔。
哦想起来了,将集合排序后每次添加一个新数 \(a\) 时,若 \(a\) 大于了当前将臣数,那 \(a\) 就大于等于丛雨数,否则可以利用 \(a\) 表示出从 \(1+a\) 到 将臣数\(+a\) 的所有数,这就可以使将臣数拓展 \(a\) 位,得证。
有了这个我们就可以每次把将臣数拓展到小于等于当前将臣数 \(+1\) 的值的和,发现若能拓展,则每次都会至少使将臣数翻倍,所以直接做就是 \(\log_V\) 的。
那么我们需要一个能够维护区间中小于等于某一值的数之和的数据结构,主席树即可。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
const int N=1e9;
int n,m,a[100100];
int rt[100100],cnt;
struct{
int ls,rs,sum;
}tr[100100*64];
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define mid ((l+r)>>1)
#define up sm(id)=sm(ls(id))+sm(rs(id))
void copy(int &to,int fr){
to=++cnt;
tr[to]=tr[fr];
}
void insert(int id,int l,int r,int x,int y){
if(l==r){
sm(id)+=y;
return;
}
if(x<=mid){
copy(ls(id),ls(id));
insert(ls(id),l,mid,x,y);
}
else{
copy(rs(id),rs(id));
insert(rs(id),mid+1,r,x,y);
}
up;
}
int query(int idl,int idr,int l,int r,int L,int R){
if(l>=L&&r<=R){
return sm(idr)-sm(idl);
}
int ans=0;
if(L<=mid){
ans+=query(ls(idl),ls(idr),l,mid,L,R);
}
if(R>mid){
ans+=query(rs(idl),rs(idr),mid+1,r,L,R);
}
return ans;
}
string main(){
cin>>n;
copy(rt[0],rt[0]);
for(int i=1;i<=n;i++){
cin>>a[i];
copy(rt[i],rt[i-1]);
insert(rt[i],1,N,a[i],a[i]);
}
cin>>m;
while(m--){
int l,r;
cin>>l>>r;
int ans=0,t=query(rt[l-1],rt[r],1,N,1,ans+1);
while(t>ans){
ans=t;
t=query(rt[l-1],rt[r],1,N,1,ans+1);
}
cout<<ans+1<<'\n';
}
return "神秘!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB();
return 0;
}
/*
5
1 2 4 9 10
1
1 5
*/
3.6 Dynamic Rankings
题意简述
动态区间第 k 小。
题解
树状数组套主席树,其实没啥好说的,只是此时主席树的写法会有一些细节调整。
Code
#include<bits/stdc++.h>
using namespace std;
namespace kong{bool st;}
namespace zhu{
int cnt=0,rt[100100],id[2][100100],cnt0,cnt1,tot,b[200200],n,m,a[100100];
struct Murasame{
int opt,l,r,k,x,y;
}q[100100];
struct{
int ls,rs,sum;
}tr[100100*128];
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sm(x) tr[x].sum
#define mid ((l+r)>>1)
#define up sm(id)=sm(ls(id))+sm(rs(id))
void insert(int &id,int l,int r,int x,int y){
if(!id) id=++cnt,sm(id)=ls(id)=rs(id)=0;
sm(id)+=y;
if(l==r){
return;
}
if(x<=mid){
insert(ls(id),l,mid,x,y);
}
else{
insert(rs(id),mid+1,r,x,y);
}
}
int query(int l,int r,int k){
if(l==r) return l;
int x=0;
for(int i=1;i<=cnt0;i++){
x+=sm(ls(id[0][i]));
}
for(int i=1;i<=cnt1;i++){
x-=sm(ls(id[1][i]));
}
if(k<=x){
for(int i=1;i<=cnt0;i++){
id[0][i]=ls(id[0][i]);
}
for(int i=1;i<=cnt1;i++){
id[1][i]=ls(id[1][i]);
}
return query(l,mid,k);
}
else{
for(int i=1;i<=cnt0;i++){
id[0][i]=rs(id[0][i]);
}
for(int i=1;i<=cnt1;i++){
id[1][i]=rs(id[1][i]);
}
return query(mid+1,r,k-x);
}
}
#define lbt(x) (x&-x)
void Ins(int x,int v){
int y=lower_bound(b+1,b+1+tot,a[x])-b;
while(x<=n){
// cout<<"Ins"<<x<<" "<<y<<' '<<v<<'\n';
insert(rt[x],1,tot,y,v);
x+=lbt(x);
}
}
int Que(int l,int r,int k){
cnt0=cnt1=0;
while(r){
// cout<<"QueA"<<rt[r]<<'\n';
id[0][++cnt0]=rt[r];
r-=lbt(r);
}
l--;
while(l){
// cout<<"QueD"<<rt[l]<<'\n';
id[1][++cnt1]=rt[l];
l-=lbt(l);
}
return query(1,tot,k);
}
string main(){
int T;
cin>>T;
while(T--){
tot=cnt=0;
for(int i=1;i<=n;i++) rt[i]=0;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[++tot]=a[i];
}
for(int i=1;i<=m;i++){
char opt;
cin>>opt;
q[i].opt=(opt=='Q');
if(q[i].opt){
cin>>q[i].l>>q[i].r>>q[i].k;
}
else{
cin>>q[i].x>>q[i].y;
b[++tot]=q[i].y;
}
}
sort(b+1,b+1+tot);
tot=unique(b+1,b+1+tot)-b-1;
for(int i=1;i<=n;i++){
Ins(i,1);
}
for(int i=1;i<=m;i++){
if(q[i].opt){
cout<<b[Que(q[i].l,q[i].r,q[i].k)]<<'\n';
}
else{
Ins(q[i].x,-1);
a[q[i].x]=q[i].y;
Ins(q[i].x,1);
}
}
}
return "2025 年迎来劲爆围杀,让我们期待 2026!";
}
}
namespace kong{bool ed;double MB(){return (&st-&ed)/1048576.0;}}
signed main(){
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
cerr<<zhu::main()<<'\n'<<kong::MB();
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号