随机化算法总结

爬山

爬山适用于单峰函数，缺陷是容易陷入局部最优解。

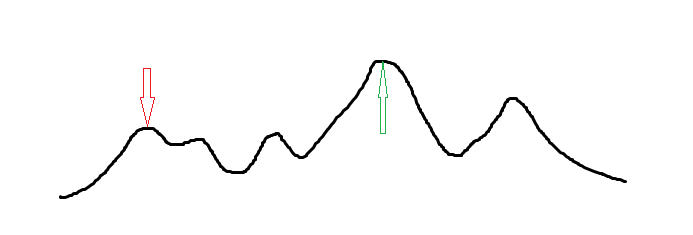
爬山的思想是每次在当前最优状态周围的状态中寻找是否有更优的状态，有就转移，具体地、设温度参数为 \(T\)，每次在 \(\pm T\) 的范围内随机取点，若更优就转移，随着转移不断将 \(T\) 乘以降温参数 \(C\)（一般取略小于 \(1\) 的常数，如 \(0.997\)），这个做法对于单峰函数是显然可行的，但是它极易陷入局部最优解，如它可能会在下图中认为答案是红色箭头所指值。

爬山相比三分的优势是可以使用更暴力的状态求解和可以处理函数有平的的情况。

模拟退火

模拟退火改进了爬山容易取到局部最优的劣势，当当前温度为 \(T\)，新状态答案比当前状态答案低 \(\Delta E\) 时仍有 \(e^\frac{-\Delta E}{T}\) 的概率转移，当然，更优仍然是绝对转移的。

需要注意的是，当已知答案函数可爬山时仍需使用爬山，因为此时模拟退火的概率接受不优解只会劣化复杂度。

还有一个优化是在退火结束后进行小范围爬山（随机扰动）看看有没有更优解。

void SA(int seed){
	double t=10000,p=0.97;
	ansx=0,ansy=0;
	answ=calc(ansx,ansy);
	mt19937 ran(seed);
	while(t>eps){
		double nx=ansx+((double)ran()*2-UINT_MAX)*t;
		double ny=ansy+((double)ran()*2-UINT_MAX)*t;
		double nw=calc(nx,ny);
		double delta=nw-answ;
		if(delta>0){
			ansx=nx;
			ansy=ny;
			answ=nw;
		}
		else if(exp(-delta/t)*UINT_MAX<ran()){//爬山算法只需去掉这三行
			ansx=nx;						  //
			ansy=ny;						  //
		}
		t*=p;
	}
	for(int i=1;i<=1000;i++){
		double nx=ansx+((double)ran()*2-UINT_MAX)*t;
		double ny=ansy+((double)ran()*2-UINT_MAX)*t;
		double nw=calc(nx,ny);
		double delta=nw-answ;
		if(delta>0){
			ansx=nx;
			ansy=ny;
			answ=nw;
		}
	}
}