一文吃完网络流！学习笔记+习题讲解！

网络流小结

latex 很多加载会很慢（（（

什么？为什么这篇叫小结？

前言

本文为了让语言更平和，加入了很多的学术无关内容，精简版。

猜一手这将成为最长的一篇（

update on 2025.5.13：markdown什么时候出七级标题啊😫

update on 2025.5.26：全文共 45KB，24565 字符，共用时 17 天，预计阅读需要不知道多久。

考虑这篇实在太几把长了所以给读者本地 pdf 版和本地 html 版，读者可按自身喜好选择阅读方式（读完了别忘了回来点赞啊）

为了方便理解，建议在读形式化题面前读一遍原题面。

本篇的模板代码都在这里ovo。

一些可能重要的东西：

实际建图时直接连剩余流量，不需要区分“流量”和“容量”，~~所以作者写题解时也会把这两个概念混淆~~。
除上下界网络流，实际建图时不需要考虑流守恒。
什么费用，上界，下界的，都可以理解为给边多了一个状态以便于求解，不要被名字束缚。
上下界网络流建图可以全按有源汇上下界费用可行/最大流建，除了常数大无缺点还好想。
不一定一个边会用上所有的状态，不要因为整张图流量都是无限或者有的边只用上了一两个状态觉得别扭。

算法总介

总介->总的介绍，这里会放基本定义和算法的一些特性。

前言

网络流有点类似 dp 的 pro 版本，板子更难，应用范围也很广，藏得也可以及其深。

一句话来说，它是一种通过构造 DAG 来解决问题的思想

基本定义

怎么这么像规则怪谈啊（

定义名词“网络” 为 $G=(V,E)$，其中 $V$ 是点集， $E$ 为边集。
对于一条边 $u\to v$，$c(u,v)$ 为其容量，$f(u,v)$ 为其流量，流量必须不大于容量。
对于 $G=(V,E)$，令 $s\in V$ 为其源点， $t\in V$ 为其汇点。
特殊地，$s$ 无入度， $t$ 无出度。
对于任意点 $u\in V$，定义其净流量为所有流入减所有流出。
流守恒：对于除了 $s$ 或 $t$ 的任意点，其净流量为 $0$。
定义一个点的剩余流量为其容量减流量。
定义剩余流量不为 $0$ 的边组成的图为残留网络。
对于 $G=(V,E)$，其整张网络的流为源点流出的量。

最大流

定义

网络流怎么 jiba 这么多定义？

增广路：注意到只要残留网络中只要有 $s\leadsto t$，就可以对路径上的流量都增加而不违背流守恒与流量不大于容量的限制，这条路就叫增广路。
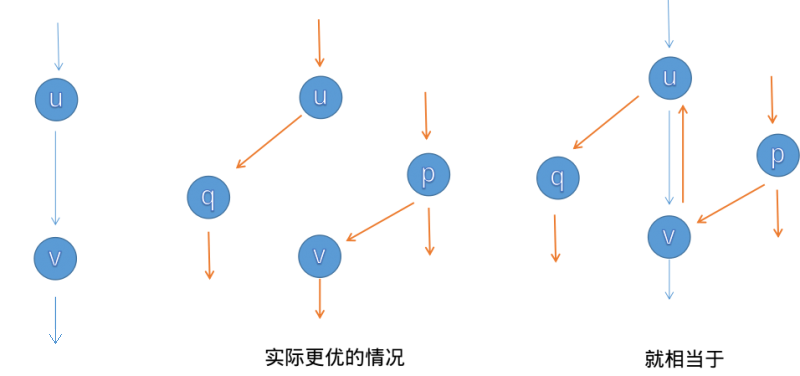
反向边：注意到如果我们单纯找到增广路就增广显然是一个伪的贪心，所以考虑让其能自然地反悔。

我们令 $u\to v$ 的反向边 $v\to u$ 的 $f(v,u)=-f(u,v),c(v,u)=0$，于是正向边剩余流量的减少就是反向边流量的增加，反之亦然。

不难发现反向边的增广就能抵消正向边的操作，并且只要进行增广，图的流肯定会变大，于是就可以通过反向边的思路求最大流。

Dinic

Dinic 的本质是对暴力的优化『感叹号』『感叹号』『感叹号』『壹』『壹』。

朴素 Dinic

考虑增广前对图按找到 $s$ 的距离进行分层，每次只增广最短的增广路。

具体地，通过 bfs 对图分层后用 dfs 找增广路。

完全体 Dinic

主播主播，你的朴素 Dinic 确实强悍，但还是太暴力了，有没什么既省码量又有效的优化呢？

有的兄弟有的，这样的优化我们还有 93个，都是当前版本 T0 级别的实用！

当前弧优化

这个最重要，能直接把复杂度降为 $O(n^2m)$，证明不会略。

注意到对节点 $u$ dfs 时我们肯定将当前边之前的边都增广到了极限，没有继续增广的价值，所以对于 dfs 到任意一条边后都将起点的 $head$ 更新到当前边。

剩余流量判断

显然有：如果上一层节点传递的流量已经消耗完了，就不用再进行 dfs。

无用节点删除

如果我们将一些流量传给下一层节点，但是下一层节点返回的流量为 0，意味着这个节点无法再进行增广，我们将它删除，这个正确性也挺显然的。

具体地，可以把其放到第 0 层。（bro 卡进后室了）

ISAP

主播主播，你的完全体 Dinic 确实强悍，但维护深度每次都重新 bfs 看起来还是太愚蠢了，有没有什么既不用做大改动又有效的优化呢？

有的兄弟有的，这样的优化我们还有 91个，都是当前版本 T0 级别的实用（存疑）！

好吧其实 ISAP 的常数不见得比 Dinic 小🤷‍♂️。

算法实现

只跑一遍从 $t$ 到 $s$ 的 bfs，显然这个虽然倒着了但是不影响正确性。
对于任意点，如果从上个点传来的流量它没有用完，那它显然是被榨干♂了，没有剩余价值了，我们将这个点的 $dep$ 加一，这样它就不会从上一个点再次转移过来了。
我们动态维护每一层的节点数，如果有一层没有节点，那么就结束算法。
如果 $dep_s>n$ 那么也结束算法，因为一共就 $n$ 个点。

详细揭秘

因为只有 $dep$ 连续才能转移，所以我们的第一条增广路肯定是最短的。

当我们的一条增广路增广完后，我们想找一条比他更长的增广路，那么我们就要将当前点的 $dep$ 增加加到能到别的节点，也就是 $dep_x\leftarrow \min(dep_v)+1$，但有注意到如果当前点都被榨干了，那它的儿子肯定也被榨干了，所以它的儿子的 $dep$ 必然也已经增加了，所以只用让 $dep_x\leftarrow dep_x+1$ 即可。

例题

这次最大流的例题题面都很阳间呢！😍

[SCOI2007] 蜥蜴

题目大意

原题晰。

题解

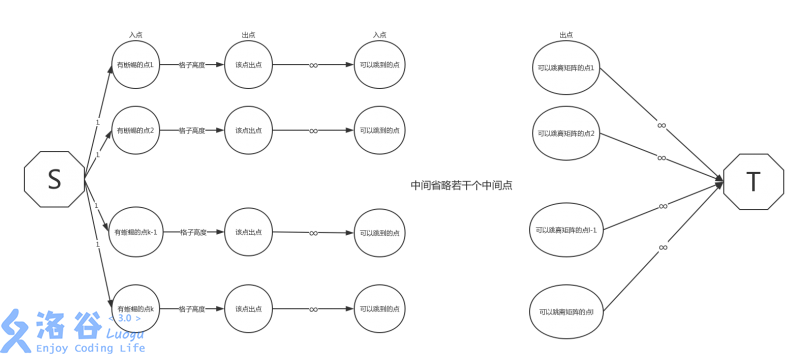
考虑将问题转化为最多有几只蜥蜴能逃离。

接着把点拆成入点出点两部分，显然它们间的连边的容量就是柱子的高度（能跳的次数）。

拿源点和所有点的入点连容量为 $1$ 的边（初始蜥蜴），然后拿汇点和所有点的出点连容量无限的边即可。

豪图我盗

[SDOI2015] 星际战争

题目大意

原题晰。

题解

看到这个小数就开始想到会被精度卡得死去活来，但是！

输出结果与标准答案的绝对误差不超过 $10^{-3}$ 即视为正确。

所以起手一个超级加倍把护甲值乘 $10000$，然后开个 long long，剩下的就让它自然取整吧~

然后再仔细读题，不难想到对于最优解的问题的常见解：对时间二分转化为可行性问题。

对于激光武器 $i$，它能在 $t$ 秒的时间内打的输出就有 $t\times B_i$，所以把源点对每个激光武器连容量为 $t\times B_i$ 的边。

对于机器人 $i$，它能承受的伤害就是 $A_i$，所以把每个机器人对源点连容量为 $t\times B_i$ 的边。

[BZOJ1458] 士兵占领

题目大意

原题晰。

题解

考虑将最少个数的士兵转化为先全放满士兵，再一个个删去，最多能删几个。

然后考虑将 $x,y$ 坐标转化为点，将 $x$ 坐标转化的点对 $s$ 连，容量为这一行最多能删几个，$y$ 坐标转化的点对 $t$ 连，容量为这一列最多能删几个，跑最大流即可。

[HNOI2007] 紧急疏散

题目大意

原题晰。

题解

~~这篇要水估值写详细点~~。

考虑到这道题的 $n,m$ 值都非常小，可以预处理出每个空地到每个门的最短路，之所以不只找最近的门是因为可能会有门“排长队”反而不优。

然后这种最优问题的一个常见解决方法就是二分需要的时间然后判断是否可行。

于是我们就考虑建图，但是一个问题是一秒只能有一个人进门处理很麻烦，所以考虑对门按时间拆点。

每个门拆出的点对下一时刻连容量无限边来模拟人们“等待”排队。
每个门拆出的点对汇点连一条容量为 1 的边来模拟每秒只能一秒只能有一个人进门。

接着让每个空地向每个能在当前限制时间内到达的门的对应时刻连容量为无限的边。

最后从源点向每个空地连边图就建好了。

最大流如果等于总人数就是能在限制时间内让所有人逃出。

[SCOI2012] 奇怪的游戏

题目大意

原题晰。

题解

这种多米诺骨牌的题显然要黑白染色，然后令有 $H$ 个黑点，总和为 $h$$，$$B$ 个白点，总和为 $b$，最后让所有数字变成 $X$，有：

\[~~~~~~~~~~~H\times X-h=B\times X-b\\ \Rightarrow (H-B)\times X=h-b \]

当 $H=B$ 时，就意味这 $n$ 和 $m$ 中必有一偶，所以此时的 $X$ 有单调性（$X$ 可行就可以再铺一层让 $X+1$ 可行），可以二分。

check函数

我们先把所有黑点对 $s$ 和连容量为需要操作次数的边，再把黑点和相邻的白点连无限容量的边，最后让白点对 $t$ 连容量为需要操作次数的边，最后判断最大流是否等于总操作次数即可。

这样显然是正确的吧。

当 $H\neq B$ 时，注意到可以直接移项把 $X$ 算出来，只用用 check 判断是否合法即可。

最小割

终于是进入了下一板块啊！

定义

对于一个网络 $G$，若能将其划分为两个点集 $S,T$，满足 $s\in S,t\in T$，则称 $\{S,T\}$ 是 $G$ 的一个割。

最小割则是求割除总容量最小的边后能将原图分成 $S$ 和 $T$ 两部分的容量和，即使 $\sum\limits_{u\in S}\sum\limits_{v\in T}c(u,v)$ 最小。

性质

最小割=最大流

证明

引理1

对于任意流 $f$ 与割 $\{S,T\}$，有 $|f|\le||S,T||$，其中取等当且仅当从 $S$ 到 $T$ 的边都是满流而从 $T$ 到 $S$ 的边都为空流

这里的 $|f|$ 为流 $f$ 的流量，$||S,T||$ 为割 $||S,T||$ 的 $\sum\limits_{u\in S}\sum\limits_{v\in T}c(u,v)$

证明：

注意下面的 $f$ 为流，$f(x)$ 为 $x$ 的净流量，$f(x,y)$ 为边 $x,y$ 的流量。

\[\begin{aligned} |f|&=f(s)\\ &=\sum_{u\in S} f(u)\ \ \\\ &=\sum_{u\in S}(\sum f(u,v)-\sum f(v,u))\\ &=\sum_{u\in S}(\sum_{v\in S} f(u,v)+\sum_{v\in T}f(u,v)-\sum_{v\in S} f(v,u)-\sum_{v\in T}f(v,u))\\ &=\sum_{u\in S}(\sum_{v\in T}f(u,v)-\sum_{v\in T}f(v,u))+\sum_{u\in S}\sum_{v\in S} f(u,v)-\sum_{u\in S}\sum_{v\in S} f(v,u)\\ &=\sum_{u\in S}(\sum_{v\in T}f(u,v)-\sum_{v\in T}f(v,u))\\ &\le\sum_{u\in S}\sum_{v\in T}f(u,v)\ \ \ (此时如果要取等就要让\ \{(u,v),u\in T,v\in S\}\ 都是空流)\\ &\le\sum_{u\in S}\sum_{v\in T}c(u,v)\ \ \ (此时如果要取等就要让\ \{(u,v),u\in S,v\in T\}\ 都是满流)\\ &=||S,T|| \end{aligned} \]

引理2

对于任意一个网络，总会存在流 $f$ 和割 $\{S,T\}$ 使得 $|f|=||S,T||$。

证明：考虑直接给出构造：

考虑在增广到得到一个流 $f$ 后，网络上不存在 $s\leadsto t$，这时取与 $s$ 同一个联通块的点组成 $S$，剩余的组成 $T$，那么因为正边都被增广完了，反边本身容量都为 $0$，所以此时有：从 $S$ 到 $T$ 的边都是满流而从 $T$ 到 $S$ 的边都为空流。

那么注意到对于最大流 $f'$ 和最小割 $\{S',T'\}$，有：

（由引理 1 知）$|f'|\le||S',T'||$。
（由引理 2 知）因为必然有 $|f|=||S,T||$ 且 $|f'|\ge |f|,||S',T'||\le||S,T||$,所以有 $|f'|\ge||S',T'||$。

至此，最小割=最大流得证！🎈🤏😆

例题

[国家集训队] happiness

题目大意

原题晰。

题解

考虑把最大的喜悦总和转化为先让条件全满足，再往下减去必须要减得。

我们对于两个相邻的点 $x,y$ 建出如下图：

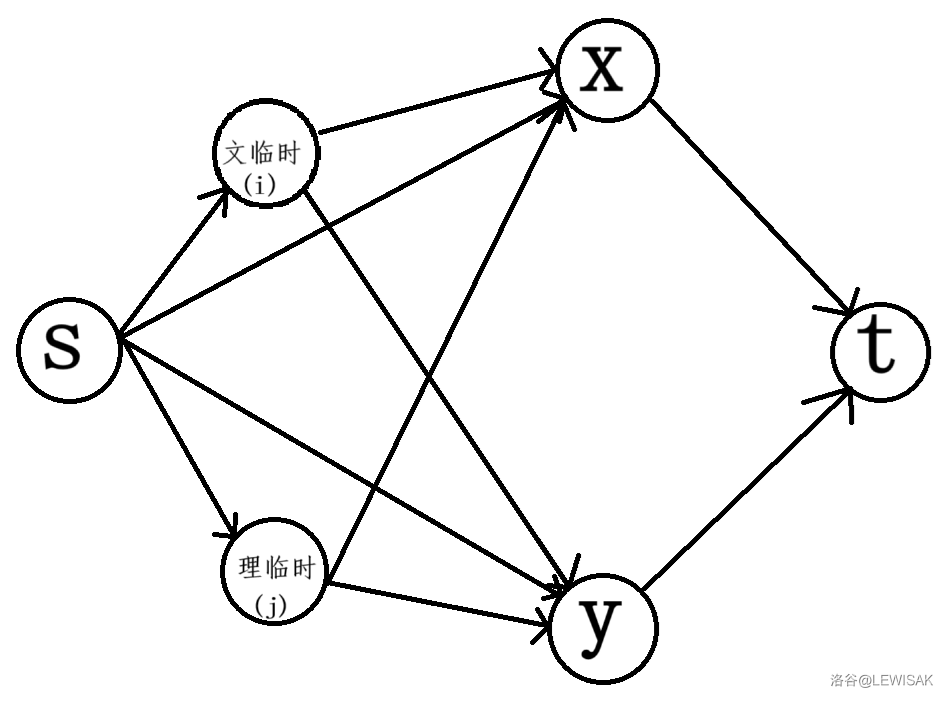
也就是造两个临时点 $i,j$ 来储存文科和理科的贡献。

具体的，连 $s\to i$ 容量为让 $x$ 和 $y$ 都选文科的喜悦值，$i\to x,i\to y$ 容量无限，$s\to x$ 容量为让 $x$ 选文科的喜悦值 $x\to t$ 容量为让 $x$ 选理科的喜悦值。

[TJOI2015] 线性代数

题目大意

原题晰。

题解

\[\begin{aligned} D&=(A*B-C)*A^T\\ &=\sum_{i=1}^{n}(\sum_{j=1}^{n}A_j*B_{j,i}-C_i)*A_i\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n}A_i*A_j*B_{i,j}-\sum_{i=1}^{n}C_i*A_i \end{aligned} \]

然后就是显然的了，注意到对于 $B$ 中的元素 $B_{i,j}$，不选损失 $B_{i,j}$，否则损失 $C_i,C_j$。

于是考虑让源点向 $B$ 中的元素连容量为 $B_{i,j}$ 的边，$B_{i,j}$ 向 $C_i$ 和 $C_j$ 连容量无限的边，$C_i$ 向汇点连容量 $C_i$ 的边即可。

[国家集训队] 人员雇佣

题目大意

选点，选点 $i$ 会增加对于所有选的点 $j$ 的 $E_{i,j}$ 的贡献，减少 $A_i$ 的贡献。

对于所有不选的点 $i$ 会减少对于所有选的点 $j$ 的 $E_{i,j}$ 的贡献，求最大贡献。

题解

我们连 $s\to i$ 容量为 $\sum^n_{j=1}E_{i,j}$，所有的 $i$ 向汇点连容量为 $A_i$ 的边，$i\to j$ 连流量为 $E_{i,j}\times2$ 的边（抵消贡献）即可。

[bzoj3158] 千钧一发

题目大意

选数，选择 $i$ 会增加 $b_i$ 的贡献，对于任意两个选的点 $i,j$ 必须满足条件：① $a_i^2+a_j^2$ 不为完全平方数 ② $a_i$ 与 $a_j$ 不互质，求最大贡献。

题解

首先把最大贡献转换为刚开始有所有贡献，要让减的贡献最小。

然后对于建图就发生了分歧：

人类智慧

考虑如果我们想建图肯定要对不能在一起的匹配，然后我就不会了😣。

但我们可以大胆猜想：对于不能同时选择的点进行连边后连出的图一定是二分图，经过验证发现的确如此。

于是对于这个二分图的左部对 $s$ 连边，右部对 $t$ 连边之后跑最小割就可以在一个式子都没有推的情况下A掉了😤。

正解

不难发现这样两条性质：

对于两个偶数，一定满足条件 $2$。
对于两个奇数，一定满足条件 $1$。

于是奇数一边偶数一边即可🤡。

[HNOI2013] 切糕

题目大意

在一个 $P\times Q$ 的矩阵中填值 $\le R$ 的数，要求相邻格子填的数之差 $\le D$，在 $i,j$ 填 $k$ 会产生 $v(i,j,k)$ 的贡献，求最小贡献。

题解

省流：

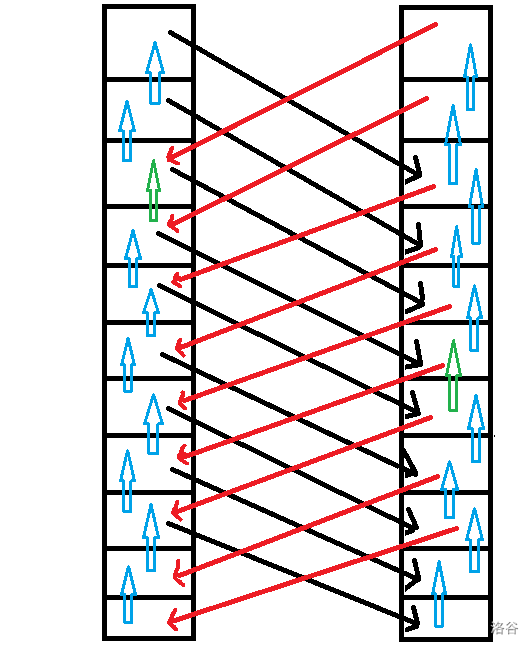
首先不考虑 $D$ 的限制，那么这个问题简直就是这个👎。

为了方便转换点权，我们新建立一层虚拟层 $R+1$。

先连 $S$ 到第一层的边和 $T$ 到第 $R+1$ 层的边，容量都是无限，再连 $i,j,k$ 到 $i,j,k+1$ 的边，容量为 $v(i,j,k)$，显然此时的最小割就是答案。

然后考虑 $D$ 的限制，我们就要让如果切掉的边是离得近的就让它能继续通行，连上图的红黑边即可，这里的红黑边容量无限。

我们考虑切掉两个绿边，注意到此时从左侧底部出发仍然能到达顶部。

[AHOI2009] 最小割

题目大意

求哪些边是最小割的可行边，那些是必须边。

题解

炒鸡无敌结论题（

首先，最小割肯定在最大流进行到一定阶段的满流上。

注意到跑最大流后，在剩余网络环上的边显然不是最小割，让流沿着环流动一圈,最大流不变,但是满流被破坏。

于是 tarjan 缩点，注意到直接连接 $S$ 和 $T$ 所在强联通分量的肯定要割，其他连接两个联通块的就是可行边。

[CQOI2016] 不同的最小割

~~这题要水估值写详细点~~。

题目大意

求对于所有点对的最小割的不同值个数

题解

这里要介绍一个新科技，最小割树。

我们注意到最小割会将图分为两个联通块，如果我们把联通块视为子树，最小割视为边，那么你会发现这就是一颗树！

具体实现上，为了方便我们找 $s$ 和 $t$ 分别的联通块，考虑割完后从 $s$ 为起点跑 bfs 求深度后将点按深度排序把不能到达的扔后面，于是 $s$ 的联通块就是左子树，$t$ 所在的联通块就是右子树，在建树时把所有最小割存进 set 里，答案即为 set 的大小。（set 自动去重）

[CQOI2017] 老C的方块

~~这篇要水估值写详细点~~。

题目大意

原题晰。

题解

提供一种只用 $10$ 行的优雅建边方式。

首先这种题看着就很像染色，不难想到应该让所有的图形都能占所有的颜色恰好 $1$ 次以便于建图，也就是说需要有 $4$ 种颜色。

经过了 $1.5$ 个小时的简单枚举后，我找到了这样一个染色方案：

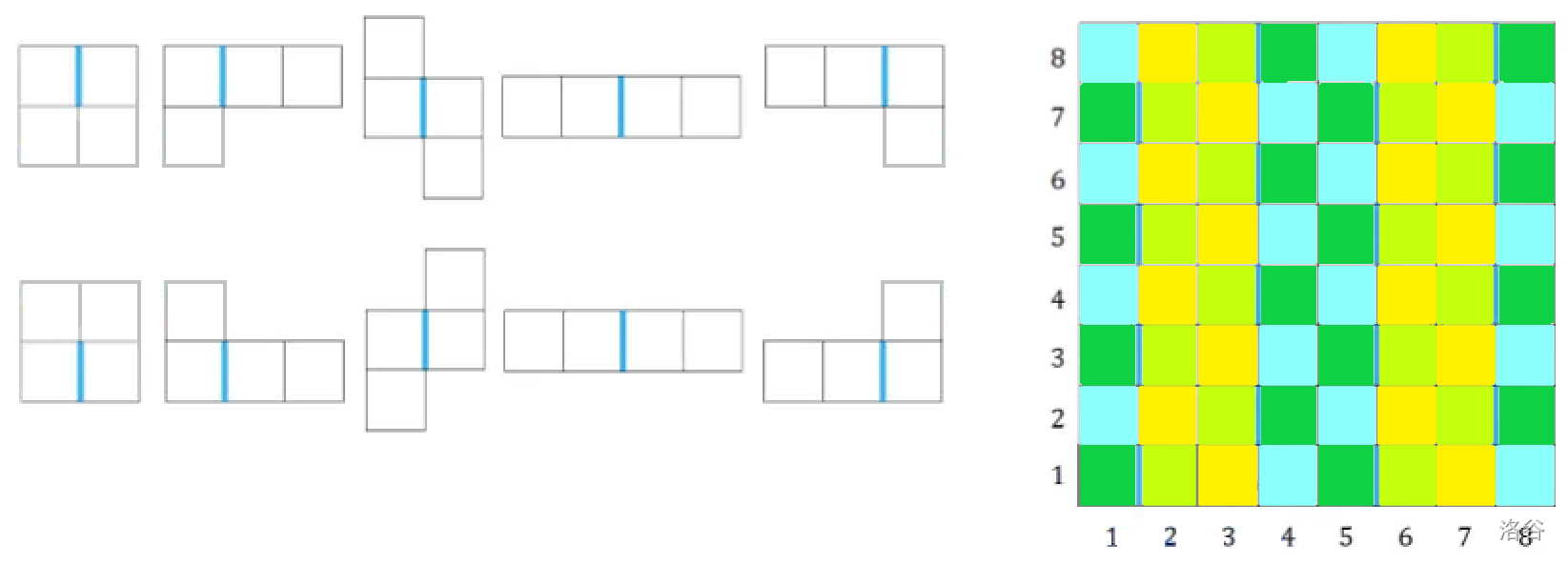
读者可以把左边的图形带入右边，以此我们发现任意图形都可以按亮黄、浅绿、深绿、淡蓝的顺序走出来，那么这个时候建图就浮出水面了。

我们不难想到，对于所有存在的点，把 $s$ 向所有亮黄点连，然后亮黄向浅绿连，浅绿向深绿连，深绿向淡蓝连，最后把所有淡蓝向 $t$ 连，这就是一个显然的最小割模型了。

可这个时候我们发现题目的删点是带权的，根据知识积累，我们不难想到可以把点权转化为边权，具体地，把所有的点拆为入点和出点，对于上述的边流量全部设为 $inf$，边的起点改为该点的出点，边的终点改为该点的入点，最后把入点向出点连流量为删除该点费用的边即可。

具体实现上，可以将亮黄、浅绿、深绿、浅蓝分别编号为 $0,1,2,3$，然后对于一个编号为 $x $ 的点向周围的编号为 $x+1$ 的点连边（注意当 $x$ 为 $3$ 时恰好不会向任何点连边），$s$ 连接所有编号为 $0$ 的点，所有编号为 $3$ 的点向 $t$ 连边。

时间复杂度证明上，这里引用我代码中的一句话：

如果这个能过那就是说我们带 $8$ 倍常数的 $n^3$ 算法通过了 $n\le 1e5$，然后我这辈子都不会想要去证明网络流复杂度了。

我这辈子都不会想要去证明网络流复杂度了。

费用流

定义

就是对每一条边加了个权值 $w_{u,v}$，定义对于一条边的花费为 $w_{u,v}\times f_{u,v}$，求：在满足最大流的前提下使得花费最小/大的花费和流量。

Dinic/EK 求费用流

把它们算法中的 bfs 换为 spfa 即可，无需脑子即可实现。

ISAP 求费用流（

经过了不知道多久的钻研后，我认为这个算法反正我是难以实现了😭。

ISAP 不能直接求费用流的原因是因为它最核心的层数思想失效了—如果你想要延续这个思想，你就需要在某个点在走第 $k$ 短路的情况下被榨干后把它的标号改为从 $k+1$ 更新出来的，这个思路一眼让复杂度伪。

有兴趣的研究新算法的请移步，可能我的一些思考会对你有帮助吧。

原始对偶算法求最小费用最大流

这就是神！~~要水估值写详细点~~。

在讲解这之前，我们要先介绍另一个算法。

Johnson 全源最短路径算法

这个算法用来求什么看算法名都能看出来吧。

我们注意到 dij 的复杂度非常的优秀，但是如果有负边权它就死了。

所以我们考虑对原图的边权进行处理使得在不改变答案的情况下使得边权非负。

一个伪的没边的方法是把所有边权都加上一个定值后统计答案时减去。

这个方法伪的地方是因为我们最短路时会受这个定值的影响，每多走一条边就会让距离多一个不该多的定值。

算法实现

新建一个虚拟点 0，并将它与所有点连一条边权为 0 的边，然后以 0 为起点跑 spfa 后对于边 $u\to v$ 的边权 $w_{u,v}$ 修改为 $w_{u,v}+h_{u}-h_{v}$。

正确性证明

我们注意到修改边权后对于一条路径 $s\to x_1\to x_2\to\dots\to x_n\to t$ 的长度为：

\[\begin{aligned} &~~~~~~w_{s,x_1}+h_s-h_{x_1}+w_{x_1,x_2}+h_{x_1}-h_{x_2}+\dots+w_{x_n,t}+h_{x_n}-h_{t}\\ &\Rightarrow w_{s,x_1}+w_{x_1,x_2}+\dots+w_{x_n,t}+h_s-h_{t} \end{aligned} \]

也就是说相较于原路径，我们多了 $h_s-h_t$ 的长度，但这个显然是定值，减掉即可。

然后我们还要证明关键的性质：所有边权为正。

注意到一个显然的事情 $h_u+w_{u,v}$ 我们可以理解是从 0 到 $v$ 的最短路但必须经过 $u$ 的长度，而 $h_v$ 就是从 0 到 $v$ 最短路长度，所以有 $h_v\le h_u+w_{u,v}$，也就是 $w_{u,v}+h_u-h_v$ 非负，也就是边权非负了！。

那有的小朋友就要问了：这个算法和最小费用最大流有什么关系呢？

我们可以先像 Johnson 一样对边权进行处理，但是问题是我们的增广会改变图的形态，所以我们要对 $h$ 动态处理。

先直接说结论：可以对 $h_i$ 加上 $s\leadsto i$ 的最短路长度 $d_i$。

首先我们刚刚证的第一个东西显然不需要重新证明，而且网络流上甚至因为我们只需要知道增广路是那条，所以连 $h_s-h_t$ 都不用减了！

现在证明边权非负：

对于增广路的边，因为它在最短路上，所以有：

\[\begin{aligned} d_i+(w_{i,j}+h_i-h_j)&=d_j\\ w_{i,j}+(d_i+h_i)-(h_j+d_j)&=0 \end{aligned} \]
于是非负。
对于增广后多的边（增广路上边的反向边）：

\[\begin{aligned} d_i+(w_{i,j}+h_i-h_j)&=d_j\\ d_i-(w_{j,i}-h_i+h_j)&=d_j\\ (w_{j,i}-h_i+h_j)+d_j-d_i&=0\\ w_{j_i}-(h_i+d_i)+(h_j+d_j)&=0 \end{aligned} \]
其中第一行推出第二行的原因是反向边的边权为正向边边权的相反数，于是非负。
对于其他边，和 Johnson 最后一步证明时类似的，有：

\[\begin{aligned} d_i+(w_{i,j}+h_i-h_j)&\ge d_j\\ w_{i,j}+(h_i+d_i)-(h_j+d_j)&\ge 0 \end{aligned} \]
于是非负。

然后就证完了🎉

顺此一提，这个算法的缺点是无法动态加点。

例题

[SDOI2016] 数字配对

题目大意

原题晰。

题解

考虑求 $cnt_i$ 为 $a_i$ 分解质因数后的质因数指数和。

于是配对条件简化为 $a_i$ 是 $a_j$ 的倍数并且 $cnt_i=cnt_j+1$。

考虑按照 $cnt$ 的奇偶把数字分为两个集合，对于左部连 $s\to i$ 容量为 $b_i$，费用为 $0$，对于右部连 $i\to t$ 容量为 $b_i$，费用为 $0$，对于能匹配的两个点，左部向右部连一条容量无限，费用 $c_i\times c_j$ 的边。

跑最大费用最大流即可。

[SDOI2009] 晨跑

题目大意

最小费用最大流，但是每个点只能经过一次。

题解

拆点，对于 $i$ 拆成 $i_1$ 和 $i_2$ 连 $i_1 \to i_2$ 容量为 $1$，对于原图上的边 $u\to v$ 连 $u_2\to v_1$ 即可。

[SCOI2007] 修车

题目大意

原明晰。

题解

拆点，把工人拆成 $n$ 个点，第 $i$ 个表示这是它在修倒数第 $i$ 辆车，连工人 $i$ 修第 $j$ 辆车的点与第 $k$ 辆车，容量为 $1$，费用为 $T_{k,i}$，连源点到车，工人到汇点的容量为 $1$，费用为 $0$ 的边。

跑最小费用最大流即可。

[NOI2012] 美食节

~~必养的题目搞种族歧视？~~

题目大意

修车加强版。

题解

动态加点：

对于被增广后的边，我们再去建下一层的图即可。

然后麻痹的原始对偶不能这么玩。

[SDOI2010] 星际竞速

题目大意

给定一张无向图，可以从编号低的点走到编号高的点，付出边权代价，或者付出 $a_i$ 代价瞬移到 $i $，求将每个点经过恰好一次的最小代价，第一次移动必须用瞬移。

题解

这个题有一个相当优雅的最小费用流最大流建图：

拆点，将点 $x$ 拆成 $x$ 与 $x'$，连 $s\to x$ 流量 $1$ 费用 $0$，连 $s\to x'$ 流量 $1$ 费用 $a_x$，对于原图上的边连 $x'\to y$ 流量 $1$ 费用边权，连 $x'\to t$ 流量 $1$ 费用 $0$。

这个东西的正确性在于每个点都会恰好经过一次，这样连边后虽然移动不连续了但是该走的边还是走了，而且最大流会保证它每个点到 $t$ 的连边都会被增广到。

但是，最优雅的解法未必是最实用的，当你学会上下界网络流，不妨返回来想想这个题的上下界解法，真的很简单。

[清华集训2017] 无限之环

题目大意

原题晰。

题解

一张图题解：

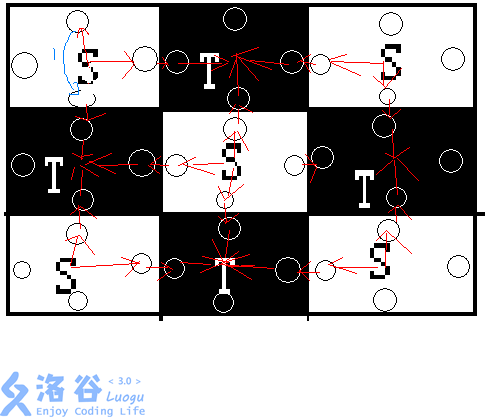
水管初始方向决定红边，水管的旋转用蓝边模拟。

然后大模拟即可。

[JSOI2009] 球队收益

题目大意

原题晰。

题解

考虑到可以先让所有球队都输，然后决策哪一队赢，这个贡献可以预处理出来。

然后对于一个队连对于任意 $x$ 连费用为赢 $x$ 场的费用，流量为 $1$ 的边即可，因为这个东西是递增的所以费用流便利第 $x$ 次时会走的对应第 $x$ 条边。

最大权闭合子图

定义

点权最大的闭合子图，它可以用于解决事件依赖问题。

啥你问我啥是闭合子图？

闭合子图内点在原图的入点也需要在闭合子图中。

实现

$s$ 连正权点，容量为点权，$t$ 连负权点，容量为点权相反数，所有点向其依赖点连边，容量无穷，答案是总点权减最小割。

证明

如果割去正权点的边即舍弃了收益，如果割去负权点的边即付出代价。

例题

[NOI2006] 最大获利

板子。

[NOI2009] 植物大战僵尸

题目大意

给定网格图，如果想击溃一个植物就要先击溃它右边的所有植物及能攻击到它本身的格子的植物，攻击成功植物的贡献可能为负，求最大贡献。

题解

考虑所有植物向其右侧和能攻击到它格子的植物连边，跑拓扑排序去掉能相互保护的植物（环），最后跑最大权闭合子图即可。

[六省联考 2017] 寿司餐厅

题目大意

寿司 $i$ 的类型是 $a_i$，如果你吃了 $i$ 到 $j$ 编号的寿司，有 $d_{i,j}$ 的贡献，如果你吃了 $c$ 个类型为 $x$ 的寿司，有 $mx^2+cx$ 的负贡献。

题解

对于 $d_{i,j}$ 连它和 $d_{i,j-1},d_{i+1,j}$ 的边，对于 $d_{i,i}$ 连它和 $a_i$ 的边，$d_{i,i}$ 有 $a_i$ 的负贡献，$a_i$ 有 $ma_i^2$ 的负贡献。

上下界网络流

这个特别好用，很多难题都可以拿这个无脑草。

定义

多了一个流的下界 $b_{u,v}$，即最少要给这条边多少流。

实现

这个东西特别牛逼，可以加各种“插件”。

belike：

无源汇上下界可行流

先讲白板：

题目大意

给定一个无源汇的网络 $G$，求是否有一个流 $f$，满足 $b_{u,v}\le f_{u,v} \le c_{u,v}$ 且流守恒。

题解

首先所有自然人应该能想到可以先让每个边都流了 $b_{u,v}$ 的流量，然后建图的时候就直接让边权是 $c_{u,v}-b_{u,v}$。

但是此时可能会让原本能守恒的流不能守恒，注意到我们误差了 $b_{u,v}$，考虑对每个点记录流出量（流出-流入），对于一个流出量为 $x$ 的点 $u$（$s$ 和 $t$ 是我们自己造的源汇）：

$x=0$：不处理
$x >0$：说明需要增加流入，连 $s\to u$ 容量为 $x$ 即可。
$x<0$：说明需要增加流出，连 $u\to t$ 容量为 $-x$ 即可。

跑最大流即可。

如何有源汇

注意到除了原本的源汇不需要流守恒其他都一样，所以考虑从原来的汇点向源点连一条容量无限的边即可。

如何最大流

在可行的基础上再跑一次从原源到原汇的最大流即可，注意如果是有源汇要先把从原汇到原源的边删去，答案是两次的和。

如何最小流

可以转换为求反向边的最大流，所以在可行的基础上再跑一次从原汇到原源的最大流，注意如果是有源汇要先把从原汇到原源的边删去，答案是可行流建第二次的最大流之差。

如何费用流

把最大流改为费用流即可。

例题

[bzoj2055] 80人环游世界

题目大意

每个国家只能向编号大于自己的飞，给定从 $i$ 到 $j$ 的费用（如果有航线的话）$d_{i,j}$，现在有 $m$ 个人从任意位置出发，求让第 $i$ 个国家恰好被经过 $V_i$ 次的最小费用。

题解

首先把国家拆点拆成入点出点，连 $s\to u,u'\to t,t\to t'$ 费用 $0$，上界 $m$，这里的最后一条边是为了防止有超过 $m$ 个人加入了这次旅行，其实前两条的上界都可以设成 $inf$ 的，对于航线 $u\to v$，连 $u'\to v$ 费用为航线费用，最后连 $u\to u'$ 上下界都是 $V_u$，费用为 $0$ 即可。

[AHOI2014/JSOI2014] 支线剧情

题目大意

给定一张 DAG，边有费用，求从 $1$ 开始把所有边都走一次的最小费用。（走到死胡同可以从 $1$重新开始）

题解

把所有的边设置一个下界 $1$，然后所有点对源点连一条无限制的边，跑最小费用即可。

[bzoj2502] 清理雪道

题目大意

给定一张DAG，定义一次操作为从任意点出发，不断前进直到到达出度为 $0$ 的点，标记沿途经过的边，求标记所有边的最小操作次数。

题解

对于所有点 $i$ 连 $s\to i$ 费用为 $1$，流量无限制，$i\to t$ 费用为 $0$，流量无限制，对于原图的边 $u\to v$ 连 $u\to v$ 下界为 $1$，费用为 $0$，上界无限制，跑最小费用即可。

怎么都这么一眼啊（

[bzoj2406] 矩阵

题目大意

给定一个矩阵 $A$，构造一个所有数值都在 $[L,R]$ 中的矩阵 $B$ 使 $A,B$ 矩阵元素差所构成的矩阵的：每一行的和的绝对值与每一列和的绝对值最小。

题解

最大值最小一眼二分答案，我们令最终的答案必须 $\le mid$。

注意到当 $A$ 矩阵某一行/列的和为 $sum$ 时，为了让两矩阵该行/列的和的差不超过 $mid$，$B$ 矩阵对应行/列的和的范围就被限制在了 $[sum-mid,sum+mid]$ 中，配合上单个元素的上下界限制，这启示我们使用上下界有源汇可行流判断。

考虑将源点与行/列连上下界为 $A$ 该行/列的和 $\pm mid$ 的边，行与列连上界 $R$,下界 $L$ 的边。

跑上下界有源汇可行流判断即可。

[NOI2008] 志愿者招募

题目大意

给定 $m$ 种人，第 $i$ 种可以从第 $s_i$ 天工作到第 $t_i$ 天，招募费用为 $c_i$，现在总共有 $n$ 天，第 $i$ 天至少要有 $a_i$ 个人工作，求最小费用。

题解

对于这种题目中有至少字眼的，考虑上下界网络流。

我们把每一天向下一天连一条下界为这一天需要人数的边，对于可以招募的人，我们连 $t_i+1\to s_i$ 费用为 $c_i$，流量不限，跑无源汇最小费用最大流即可。

[SDOI2017] 新生舞会

题目大意

给定 $n$ 个男生和 $n$ 个女生，求把他们配♂对♂，给定两个矩阵 $a,b$，另$\frac{a'_1+a'_2+..+a'_n}{b'_1+b'_2+...+b'_n}$ 最大，其中男生 $i$ 与女生 $j$ 配对会给分子加 $a_{i,j}$，给分母加 $b_{i,j}$。

题解

这是一道显然的分数规划问题，考虑二分。

另 $\frac{\sum a_i}{\sum b_i}>mid$，那么有 $\sum a_i-\sum b_i\times mid>0$，把左边的玩意当成新的费用用最小费用最大流求解即可。

对偶图

严格来说这不是一个算法，但这个 trick 很实用于是给了二级标题，它的作用是把平面图的最小割转化为最短路，因为它实际上不需要最小割算法代码了所以我没有让它隶属于最小割。

定义

平面图：如果能把图 $G$ 画在平面上，使得除顶点外，边与边没有交叉，则 $G $ 为平面图。
对偶图：将平面图的面转化为点，隔开面的边转化为两个点之间的边。

性质

平面图最小割=对偶图最短路。

证明

观察下图，不难发现所有对偶图上从起点到终点的路径都能把原图的 $s$ 与 $t$ 隔开，更严谨一点就是可以把路径上的边转化为原图上的边。

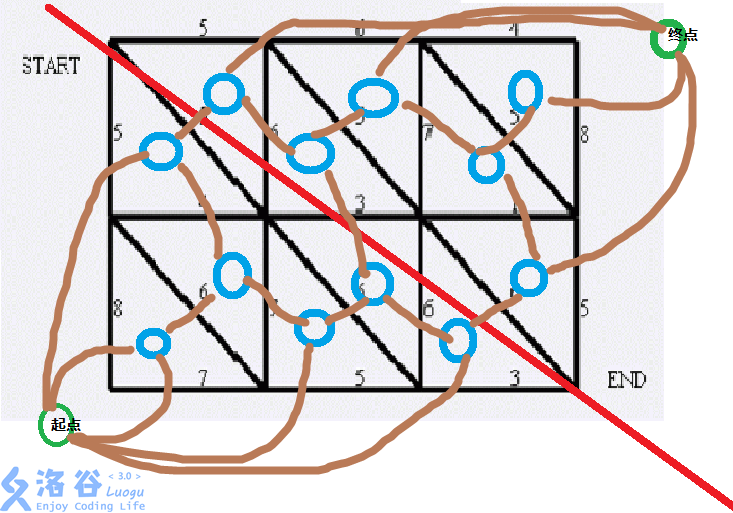
实现

逮着个边把它左右两边的面连起来即可。

例题

[ICPC2006] 狼抓兔子

题目大意

给定这样一张图：

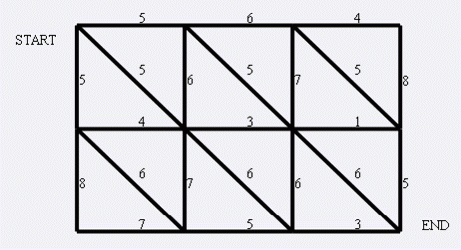
求最小割。

题解

版，按刚刚证明性质时给的图做就行。

[NOI2010] 海拔

~~水估详~~。

题目大意

给定一张带边权网格图有向图，但是 $u\to v$ 和 $v\to u$ 都有边而且边权不一样，定义一条边的代价是其两边点填的数之差乘边权后对 $0$ 取 $\max$，求最小边权和。

题解

定义：连通块为高度相同的相邻点组成的极大连通子图。

首先对于所有高度小于 $0$ 的点，全把它们补成 $0$ 显然更优，因为它们本身的贡献就被减没了，而大于 $0$ 的点在调整前后都大于等于它们，贡献只减不增，对于大于 $1$ 的同理。

接下来我们就把所有的高度缩减在了 $[0,1]$ 中，接下来证明有一种最有方案是让所有的点压成一个 $0$ 的连通块一个 $1$ 的连通块。

我们不断找到一个高度最小的不含左上角的连通块，显然除非现在只有 $0,1$ 两种高度的点并且都挤成了两个连通块，那么这个连通块也不含右下角。

当这个连通块与左上角的连通块相邻，那么我们它的一种不劣调整策略是让它的高度改为与之相邻的不包含左上角的最低连通块的高度或将其高度改为 $0$。

证明：观察下图（我们将原图的点转换为方格，线转换为方格之间的线以便于思考）：

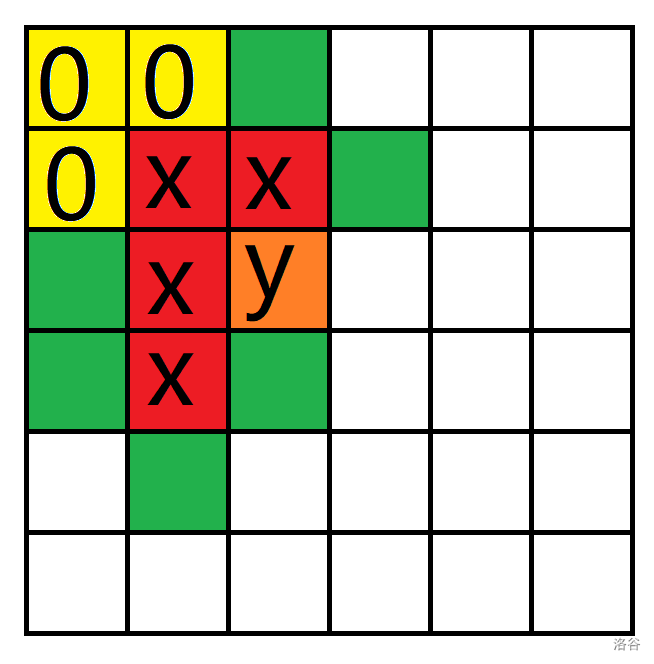
其中格子上的数字/字母表示这个格子的高度，黄色格子是左上角的连通块，红色格子是我们找到的高度最小的不含左上角的连通块，橙色格子是与之相邻的不包含左上角的最低连通块，绿色格子是与红色相邻的非橙色/黄色格子。

因为这个图上面画边权比较的麻烦，我们这里设从黄色格子到红色格子的边权和为 $a$，从红色格子到橙/绿格子的边权和为 $b$，（注意这里设的边都是从低到高的边）那么有：
- 把红色格子高度改为 $y$ 的贡献是：对于橙/绿色格子（$>x$）减少了 $(y-x)\times b$，对于黄色格子（$<x$）增大了 $(y-x)\times a$，整理后的最终贡献是 $(y-x)\times(a-b)$。
- 把红色格子高度改为 $0$ 的贡献是：对于橙/绿色格子（$>x$）增大了 $x\times b$，对于黄色格子（$<x$）减小了 $x\times a$，整理后的最终贡献是 $x\times(b-a)$。
那么这个时候注意到由于 $y>x>0$，所以只要我们当 $a>b$ 时把红色格子高度改为 $0$，否则改为 $y$，我们选择的方案就一定时不劣的，所以红色格子一定有一种不劣调整策略是让它的高度改为 $y$ 或将其高度改为 $0$，结论证毕。
当这个连通块不与左上角的连通块相邻，我们将这个连通块中所有点的高度都调整为与之相邻的最低连通块的高度（就是上图中的 $y$），注意到因为此时别的连通块对比它改前改后都是比它高的，所以贡献只减不增。

诶这个时候我们发现无论此时的情况如何都能有一种不劣的调整方案来减少连通块数量，直到所有的点都是 $0$ 或 $1$ 且已经挤成了两个连通块，于是一定有一种最优方案是让所有的点满足上述情况。

这个时候可能还有人觉得这个有点像贪心，似乎调整只能满足对于当前的不劣，但是考虑到我们随意选择另外一种最优调整策略，它都能通过不断不劣的调整成为只有左上和右下所在的两个连通块的情况。

接下来有了这个性质后就简单了，注意到 $0$ 与 $1$ 的分界处会带来边权的贡献，而 $0$ 和 $1$ 的分界绝对会把从左上到右下的所有路径切断，这就是一个最小割模型了，但是这个数据范围不允许裸跑，考虑优化。

题目给的图显然是一个平面图，我们不难想到把其转换为对偶图。

也就是：

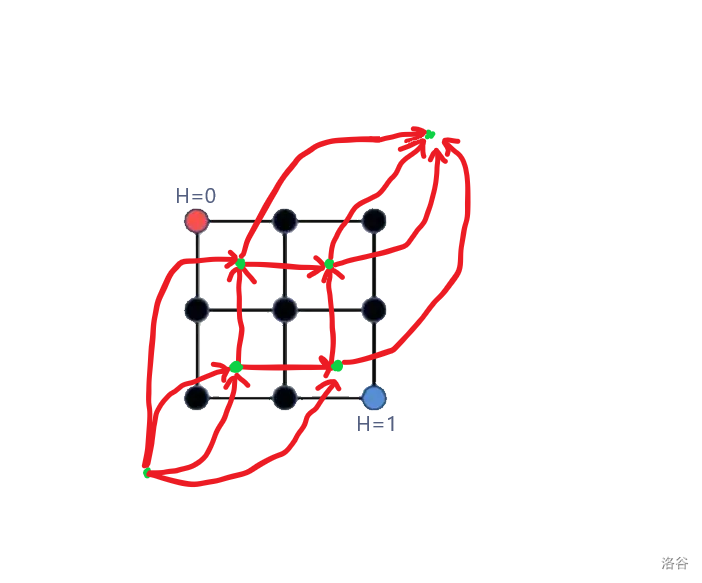
技巧整理

整理了所有题目的建图技巧~

通用技巧

对于权值在点上的问题考虑拆成入点与出点。

e.g：[SCOI2007] 蜥蜴，P2153 [SDOI2009] 晨跑
对于原本图上某个点的初始值可以转化为源点对其连边的容量。

e.g：[SCOI2007] 蜥蜴，[HNOI2007] 紧急疏散
对于花里胡哨的限制/距离，直接预处理。

e.g：[HNOI2007] 紧急疏散，[bzoj3158] 千钧一发，[SDOI2016] 数字配对
对于有有关时间的条件的，考虑对时间拆点。

e.g：[HNOI2007] 紧急疏散，[SCOI2007] 修车
对于神秘式子，试着推一下。

e.g：[TJOI2015] 线性代数，[bzoj3158] 千钧一发
对于多层图但是转移时不需要同时用所有层的，考虑动态加点。

e.g：[NOI2012] 美食节
对于填数问题，每个数都拆成一个点。

e.g：[HNOI2013] 切糕
对于限制总数的，可以对汇点拆点。

e.g：80人环游世界
当所有点都需要恰好经历一次时，可以让路径不连续建图。

e.g：[SDOI2010] 星际竞速

算法选择

对于求权值最值，最大不一定对应最大流，最小不一定对应最小割，考虑正难则反。

e.g：[SCOI2007] 蜥蜴，[BZOJ1458] 士兵占领，[国家集训队] happiness，[bzoj3158] 千钧一发
对于“要么选 A 要么选 B”的问题，考虑最小割

e.g：[国家集训队] 人员雇佣，[TJOI2015] 线性代数，[国家集训队] happiness
对于有事件依赖的问题，考虑最大权闭合子图。

e.g：[六省联考 2017] 寿司餐厅，[NOI2009] 植物大战僵尸，[NOI2006] 最大获利
对于类似买物品，买几个付几个的费用的题，考虑费用流

e.g.[SDOI2016] 数字配对，[AHOI2014/JSOI2014] 支线剧情
对于题目中有至少、恰好等字眼的，考虑上下界网络流。

e.g：[AHOI2014/JSOI2014] 支线剧情，80人环游世界，[bzoj2502] 清理雪道，[SDOI2010] 星际竞速，[NOI2008] 志愿者招募
对于数据大到难以用朴素最小割的，看看能不能转化为对偶图。

e.g：[ICPC2006] 狼抓兔子，[NOI2010] 海拔

网格类问题技巧

对于在横/纵有限制的，考虑将 $x,y$ 坐标转化为点。

e.g：[BZOJ1458] 士兵占领
对于多米诺骨牌类问题，考虑染色后对颜色连边。

e.g：[SCOI2012] 奇怪的游戏，[CQOI2017] 老C的方块

最大流技巧

对于最优解问题可以二分转化为可行性问题后用最大流判断可行性。

e.g：[SDOI2015] 星际战争，[HNOI2007] 紧急疏散，[SCOI2012] 奇怪的游戏

最小割技巧

对于两个点在一起会产生贡献，考虑建临时点连接它们，临时点和源点的容量为贡献。

e.g：[国家集训队] happiness
对于需要造一些“无敌边”时，可以通过连流量无限的边让让其割不掉

e.g：[TJOI2015] 线性代数，[国家集训队] happiness，[HNOI2013] 切糕，[bzoj3158] 千钧一发
对于不好搞的条件，可以通过让切的边不满足条件时 $S$ 仍然能到达 $T$ 来限制。

e.g：[HNOI2013] 切糕
对于要求一坨最小割的，建最小割树

e.g.：[CQOI2016] 不同的最小割

费用流技巧

对于求最大贡献的题，不要被名字所干扰，费用也可以是贡献。

e.g：[SDOI2016] 数字配对
对于求分数最小的题，考虑分数规划后重置费用。

e.g：[SDOI2017] 新生舞会
对于平方费用，考虑连多条费用递增的边。

e.g：[JSOI2009] 球队收益

最大权闭合子图技巧

对于可能有相互依赖的，拓扑消环。

e.g：[NOI2009] 植物大战僵尸

上下界网络流技巧

对于一个点要经过多少次的，拆成入点和出点。

e.g：80人环游世界
对于某个东西可以管多久时间，可以建一条“时间回溯”的边。

e.g：[NOI2008] 志愿者招募

后记

全文共 45KB，24565 字符，共用时 17 天。

跟着我学网络流的，写这么长还不点赞我就让你🐴💥～(∠・ω< )⌒★

posted @ 2025-05-16 00:03 LEWISAK 阅读(117) 评论(6) 收藏举报

刷新页面返回顶部