基环树与笛卡尔树

基环树与笛卡尔树总结

基环树

算法简介

不是算法，而是一种树的形态，就是给树加了条边，形成了一个环，可以与树上问题打组合技，得会树还会环，有些鹅心。

[ZJOI2008] 骑士

题目大意

没有上司的舞会加一条边。

题解

板子，断环后跑没有上司的舞会。

[NOIP 2018 提高组] 旅行

题目大意

求在基环树上的一个路径使得 \(dfs\) 遍历到点的顺序的字典序最小。

题解

和基环树没关系，枚举每一条边断开后 \(dfs\) 即可。

[IOI 2008] Island

题目大意

基环树上求直径。

题解

环和树分别处理，最后在环上用单调栈统计答案即可。

[POI 2012] RAN-Rendezvous

题目大意

原题晰。

题解

注意到：

• \(u,v\) 不在一颗基环树上：无解。
• \(u,v\) 不在环上同一顶点的子树内：先上跳再在环上相遇。
• \(u,v\) 在环上同一顶点的子树内：lca。

[luogu P10933] 创世纪

这篇要用来水估值写详细点

题目大意

给定一张内向基环树，求最多能选定几个点使得每个被选定的点都有至少一条未被选定的点指向它的边。

题解

特别的，以下对于 \(a_i=j\) 称 \(j\) 为 \(i\) 的父亲。

题解都是树形 dp 啊，考虑拓扑加贪心，注意到几个性质：

1. 叶子节点绝对不能被选定，于是它的父亲就一定可以被选定，于是当拓扑时遇到了叶子节点就将它和父亲删掉并把答案加一。

2. 对于一个大小为 \(siz\) 的环，答案显然为 \(\left \lfloor{siz/2 } \right \rfloor\) （隔一个选一个），拓扑后找环即可。

关于正确性，注意到将叶子和其父亲删掉最多破坏一个贡献，但一定会产生一个贡献。

笛卡尔树

算法简介

\(Treap\) 但是随机值变为了给定值（\(w\)），\(val\) 变成了数组下标（\(k\)）。

算法实现

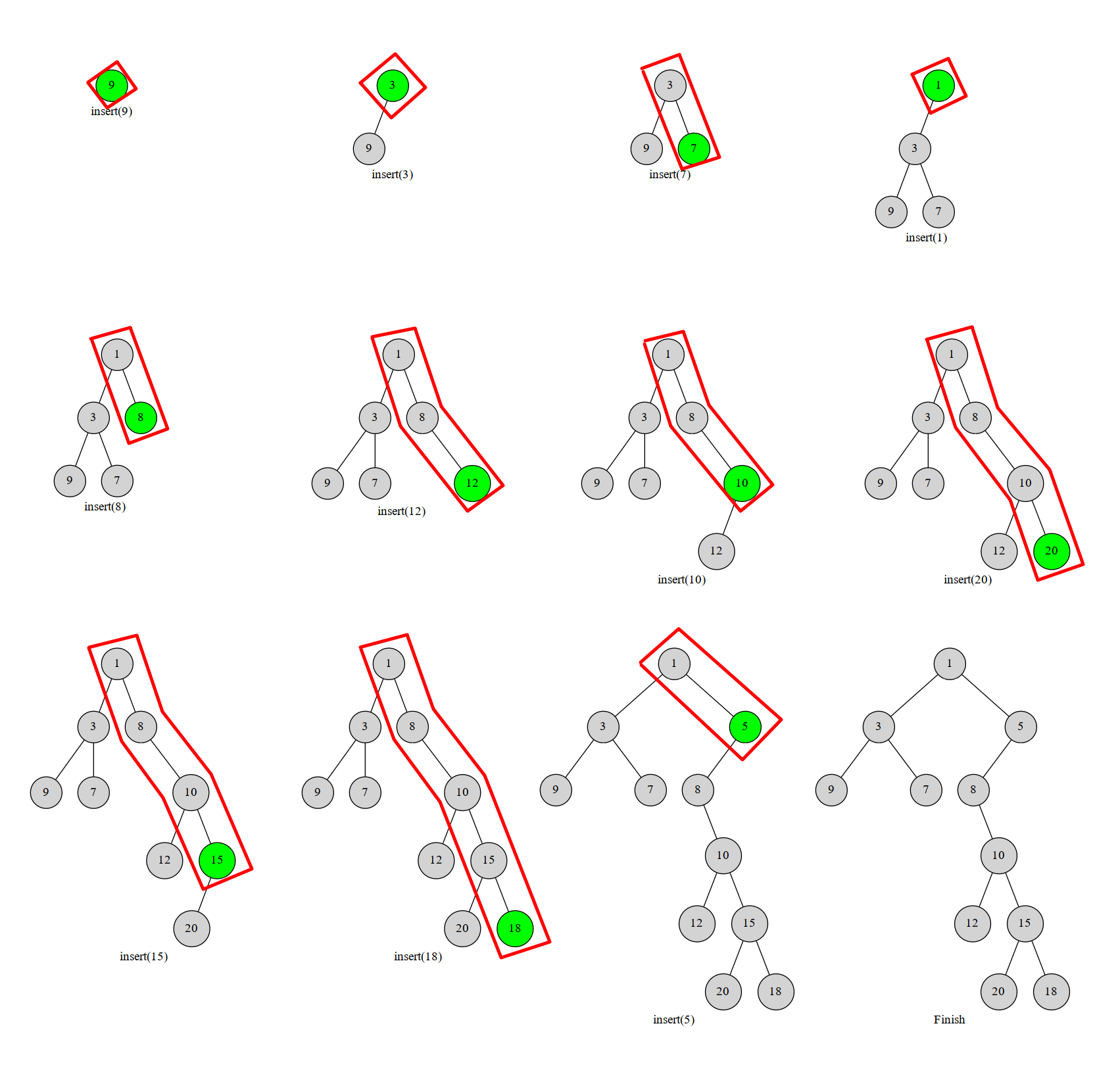
注意到我们按照数组下标添加节点的话每次加的点只会成为新的根节点或在右链的某个地方插入后将第一个 \(w\) 小于它的节点变成它的儿子，于是考虑用栈维护右链即可做到 \(O(n)\) 建树。引用一张 OI-wiki 的图：

[HDU 6305] RMQ Similar Sequence

题目大意

原题晰。

题解

考虑到 RMQ 相同就意味着对于 \(A,B\) 建造出的笛卡尔树任意对应两点的 \(\text{lca}\) 都相同，也就是同构了。

然后因为 \(B\) 是在 \([0,1]\) 中的实数，所以不妨认为 \(B\) 中所有元素不重，于是 \(B\) 的笛卡尔树唯一，然后有一句废话：

若所有子树的根节点都相同，则笛卡尔树就是同构。

于是概率为 \(\frac{1}{\prod^n_{i=1}siz_i}\)，而 \(B\) 的期望权值为 \(\frac{n}{2}\) 于是答案为 \(\frac{n}{2\prod^n_{i=1}siz_i}\)。

[COCI 2008/2009 #4] PERIODNI

题目大意

在残缺的表格上放最多数量的車，让他们在不跨过空缺的情况下无法互相攻击。

题解

和笛卡尔树没关系。

考虑把多边形转为树，一层层割即可。

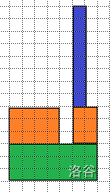
分治建树，每次从最低点分开，接着考虑树形 dp，设 \(dp_{x,i}\) 表示以 \(x\) 为根的子树放了 \(i\) 个車，\(f_{x,i}\) 表示以 \(x\) 为根除 \(x\) 放了 \(i\) 个車。

转移显然。

[hdu4125] Moles

题面长如屎，写了一堆讲定义，硬融没新意。最傻逼。

[hdu6854] Kcats

好题，坏数据范围。

题目大意

原题晰。

题解

注意到 \(a_i\) 本质是笛卡尔树上 \(i\) 号点 \(k\) 值 \(\le\) 自己的祖先数量，遂区间 dp，令 \(dp_{l,r,i}\) 表示 \([l,r]\) 的 \(a\) 值为 \(x\) 的方案数，转移：

\[f_{i,j,a_k} = {j-i\choose k-i}\times f_{i,k-1,a_k}\times f_{k+1,j,a_k+1} \]