[JLOI2014] 路径龟划

传送门

我的部落格

这个题总体很割裂，感觉是给分层图上面强行套了个数学，不过两部分的思路都挺巧妙的。

题目大意

这道题 luogu 题面不太清晰，大意给定一张无向图，你需要开车从起点走到终点，有些点会设红绿灯，给出每个红绿灯的红灯时间和绿灯时间，你见到红绿灯时红绿灯的状态随机 \(^1\)，你只能连续开油箱中储存油量时间车（等红绿灯也会耗油），到加油站会补油，求到终点的最优路线，使得：

1. 期望时间最短
2. 经过红绿的数量不多于 \(k\)。

\(1\): 状态随机指在红绿灯循环周期中的一个随机时刻（可以不是整数）

题解

数学部分

先说结论，红绿灯的期望通过时间是 \(\frac{red^2}{2(red+green)}\)，网上的证明要么不严谨要么要用积分，我来一发亲民的。

注意到当我们在周期的 \(x\) 时进入的话，贡献就是 \(\max(\frac{red-x}{red+green},0)\) ，对 \(0\) 取 \(\max\) 的原因是如果进入的时间大于 \(red\) 那么就直接通过了，然后我们以 \(8\) 秒红灯，\(1\) 秒绿灯画出函数图像：

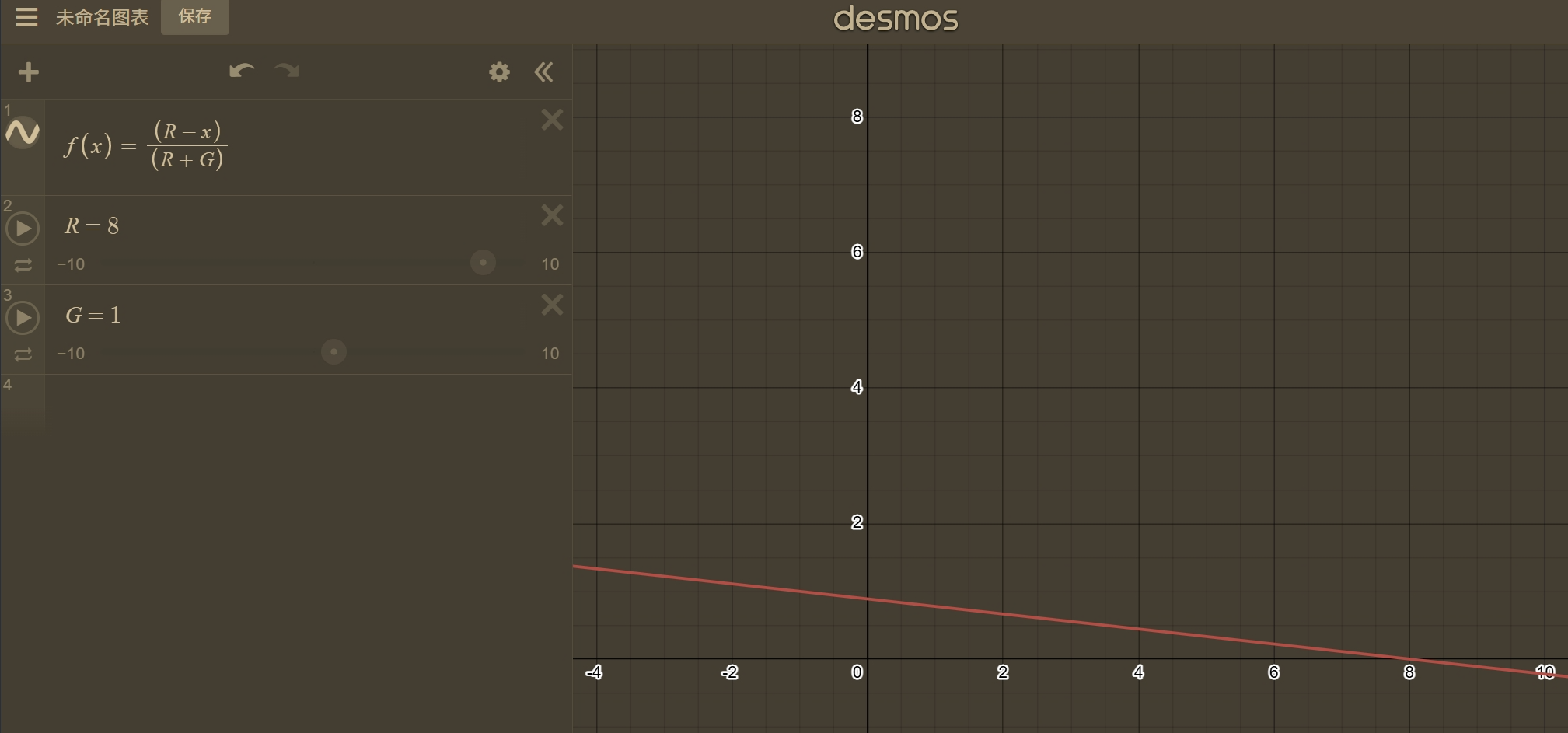
那么对 \(0\) 取 \(\max\) 就相当于不计算函数值为负的图像，再加上 \(x\) 只能为正就是只算第一象限，不难发现第一象限的贡献之和就是一个三角形：

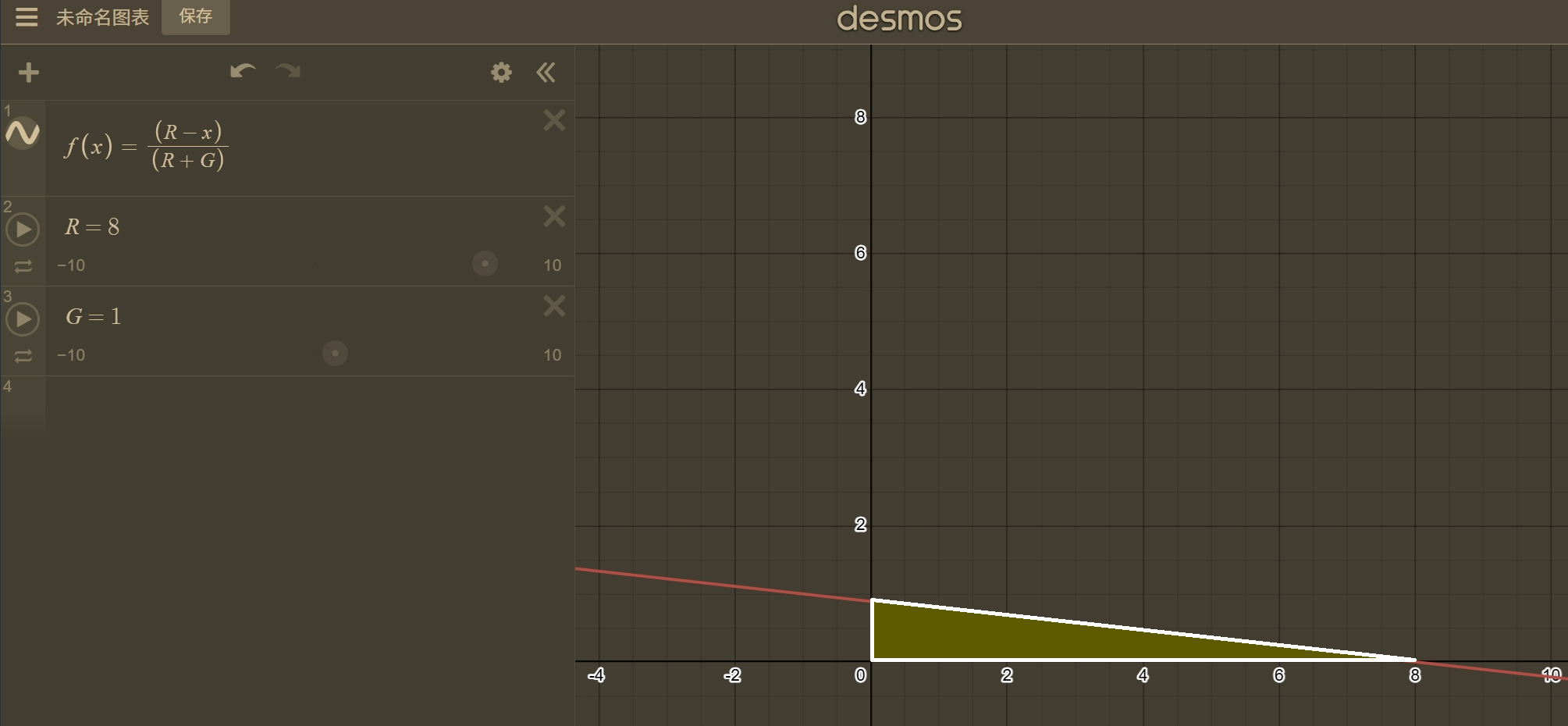
然后当 \(x\) 取到 \(0\) 时有三角形的高 \(\frac{red}{red+green}\)，三角形的底就是在第一象限时 \(x\) 能取到的最大值 \(red\)，于是有总期望为：

\[\frac{red}{red+green}*red*\frac{1}{2} = \frac{red^2}{2(red+green)} \]

算完期望后直接开一个输出储存就可以了，接下来转化成了普通图论。

图论部分

我们考虑先忽略油量限制，直接对红绿灯建分层图，理由是不多于 \(k\) 个红绿灯这个限制长得就像分层图，而且 \(k\le 5\)。

第 \(i\) 层分层图表示经过了 \(i\) 个红绿灯，在红绿灯处连接两层分层图，最后建出的图有 \(k\) 层，每层 \(n\) 个节点。

接下来考虑油量限制，注意到保证中有一个很可以的限制：

加油站数量 \(\le 50\)

于是考虑建出第一张图后枚举加油站作为起点，最短路看其他哪些其他加油站是可以跑到的，然后在这两个加油站中连边建出新图。

然后第二张图也是有 \(k\) 层，每层不超过 \(50\) 个节点，直接跑起点到终点的最短路就可以了。

最后这个题的复杂度还是证一下，瓶颈显然在于建第二张图对每个加油站跑最短路的复杂度 \(O(50kmlog_{nk})\)，计算器敲一下发现是 \(1.6e8\) 多一点，实际根本跑不满

代码

代码中最短路用的是 dijkstra。

#include<bits/stdc++.h>
using namespace std;
const int eps=1e-7;
namespace FFF{
unordered_map<string,int> dian;
int yo[200200],zhan[200200],id[200200][20],n,m,k,s,t,top,jia,kai;
double out[200200];
struct UUU{
	int tot,head[200200],vis[200200];
	double dis[200200];
	struct CCC{
		int nxt,to;
		double w;
	}e[400400];
	void add(int u,int v,double w){//链式前向星
		e[++tot].to=v;
		e[tot].nxt=head[u];
		e[tot].w=w;
		head[u]=tot;
		return;
	}
	void dij(int s){//dijkstra
	    for(int i=1;i<=n*(k+1);i++){
			dis[i]=1e9;
			vis[i]=0;
		}
		priority_queue<pair<double,int>,vector<pair<double,int> >,greater<pair<double,int> > >q;
		dis[s]=0;
		q.emplace(0,s);
		while(!q.empty()){
			int u=q.top().second;
			q.pop();
			if(vis[u]){
				continue;
			}
			vis[u]=1;
			for(int i=head[u];i;i=e[i].nxt){
				int v=e[i].to;
				if(dis[v]>dis[u]+e[i].w){
					dis[v]=dis[u]+e[i].w;
					q.emplace(dis[v],v);
				}
			}
		}
	}
}two,one;
void add(int u,int v,int w){//建分层图
	if(fabs(out[v])>eps){
		for(int j=0;j<k;j++){
			one.add(id[u][j],id[v][j+1],w+out[v]);
		}
	}
	else{
		for(int j=0;j<=k;j++){
			one.add(id[u][j],id[v][j],w);
		}
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>k>>kai>>jia;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=k;j++){
			id[i][j]=i+j*n;
		}
	}
	for(int i=1;i<=n;i++){//输入
		string st;
		int red,green;
		cin>>st>>red>>green;
		dian[st]=i;
		if(st=="start"){
			s=i;
		}
		else if(st=="end"){
			t=i;
		}
		if(st.find("gas")!=string::npos){
			yo[i]=1;
		}
		if(red){
			out[i]=1.00*red*red/(double)(2.00*(red+green));//算期望
		}
		else{
			out[i]=0;
		}
	}
	for(int i=1;i<=m;i++){//建边
		string uu,vv,zxc,fw="114514";
		double w;
		cin>>uu>>vv>>zxc>>w;
		zxc=fw;
		add(dian[uu],dian[vv],w);
		add(dian[vv],dian[uu],w);
	}
	yo[s]=yo[t]=1;
	for(int i=1;i<=n;i++){
		if(yo[i]){
			zhan[++top]=i;
		}
	}
	for(int i=1;i<=top;i++){//枚举加油站
		one.dij(zhan[i]);
		for(int j=1;j<=top;j++){
			if(i==j){
				continue;
			}
			int w=(zhan[j]!=s&&zhan[j]!=t)?jia:0;
			for(int l=0;l<=k;l++){
				if(one.dis[id[zhan[j]][l]]<=kai){
					for(int p=0;p+l<=k;p++){
						two.add(id[zhan[i]][p],id[zhan[j]][p+l],one.dis[id[zhan[j]][l]]+w);
					}
				}
			}
		}
	}
	double ans=1e9;//统计答案
	two.dij(s);
	for(int i=0;i<=k;i++){
		ans=min(ans,two.dis[t+i*n]);
	}
	printf("%.3lf\n",ans);
	return 0;
} 
}
int main(){
	FFF::main();
	return 0;
}