二分图学习笔记

定义：

节点由两个集合组成，且两个集合内部没有边的图。

例如上图就是一张二分图，其中红色部分称为左部，蓝色部分称为右部（好吧也可以反过来）。

判定：

使用染色法，用两种颜色来代替左部和右部，向外拓展时如果遇到左部连左部，右部连右部就不是二分图。

bool dfs(int x){
	for(int i=head[x];i;i=e[i].nxt){
		int v=e[i].to;
		if(color[v]==color[x]){
			return 0;
		}
		if(color[v]==-1){
			color[v]=!color[x];
			if(!dfs(v)){
				return 0;
			}
		}
	}
	return 1;
}

模版题速通：

P1525 关押罪犯

虽然并查集做法相对简单。

令最大值最小--一眼二分。

二分冲突值后判断能否将所有会产生大于 \(mid\) 的罪犯对分开即可。

人话就是判断以冲突值大于 \(mid\) 的罪犯关系连边判断是否为二分图。

点击查看代码

#include<bits/stdc++.h>//大家补药学习LEWISAK这种浪费空间的行为！
#define int long long//这是坏习惯！ 
using namespace std;
int head[100100],tot,color[100100],n,m;
struct asdf{
	int nxt,to,w;
}e[200200];
void add(int u,int v,int w){
	e[++tot].to=v;
	e[tot].nxt=head[u];
	e[tot].w=w;
	head[u]=tot;
	return;
} 
bool dfs(int x,int y){
	for(int i=head[x];i;i=e[i].nxt){
		if(e[i].w<y){//小于mid不用管
			continue;
		}
		int v=e[i].to;
		if(color[v]==color[x]){
			return 0;
		}
		if(color[v]==-1){
			color[v]=!color[x];
			if(!dfs(v,y)){
				return 0;
			}
		}
	}
	return 1;
}
bool check(int mid){
	memset(color,-1,sizeof(color));
	for(int i=1;i<=n;i++){//自己造的图不保证联通
		if(color[i]==-1){
			color[i]=0;
			if(!dfs(i,mid)){
				return 0;
			}
		}
	}
	return 1;
}
signed main(){
	cin>>n>>m;
	int maxx=0;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		maxx=max(maxx,w);
		add(u,v,w);
		add(v,u,w);
	}
	int l=0,r=maxx+1;//二分冲突值
	while(l<=r){
		int mid=(l+r)>>1;
		if(check(mid)){
			r=mid-1;
		}
		else{
			l=mid+1;
		}
	}
	if(r<0){//无解情况
		r=0;
	}
	cout<<r;
	return 0;
}

最大匹配

定义

• 匹配：从二分图中选出一些边，使得这些边没有公共顶点。

• 最大匹配：从二分图中选出一些边，使得这些边没有公共顶点，且边的数量最大。

匈牙利算法

算法思想是优先满足左部编号较后的端点，如果有冲突就先让左部编号较前的谦让，没有别的匹配就让左部编号较后的谦让，要是较后的也没有那就失配了。（具体实现见代码）

证明略，可以自己手膜几个样例就不言而喻了。

int n,m,ee,vis[1010],pp[1010],ans;//pp[i]:左部i号点的匹配 vis[i]： i是否在dfs中遍历到 
vector<int> e[1010];
bool dfs(int x){
	if(vis[x]){
		return 0;
	}
	vis[x]=1;
	for(auto v:e[x]){//l编号较后的迁就 
		if((pp[v]==0)/*右部点没匹配过别的直接匹配*/||dfs(pp[v])/*l编号靠前的能迁就就迁就*/){
			pp[v]=x;
			return 1;
		}
	}
	return 0;
}

模版题速通：

Acwing 406放置机器人

先从每个空地出发，向上向下扫进行一个建的图：

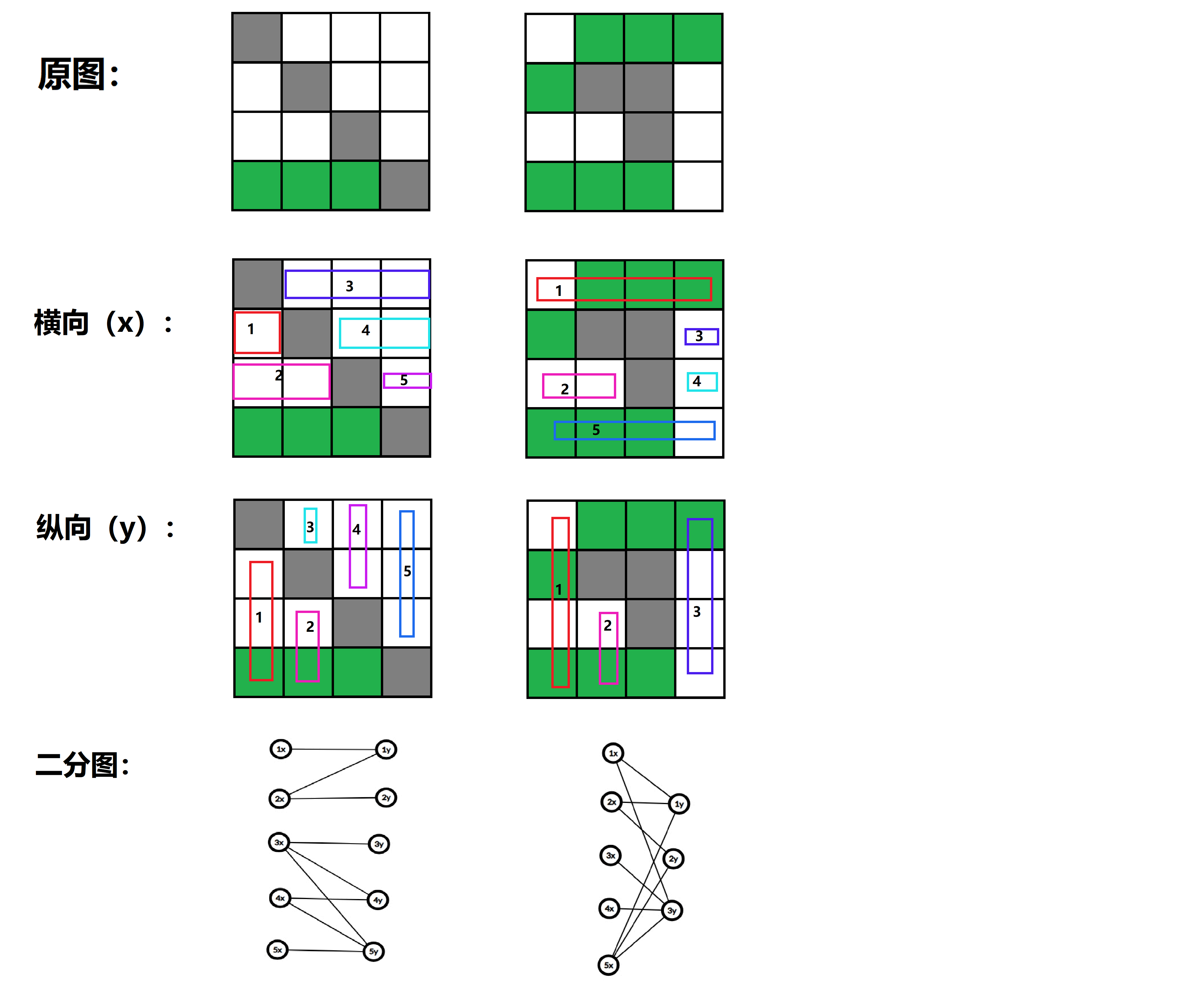
然后跑最大匹配即可，原理是每个空地都会使一行，一列无法放别的机器人。

代码实现有点 tarjan 缩点的感觉

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m,ee,vis[1010],pp[1010],ans,x[1010][1010],y[1010][1010],cntx,cnty;
char mp[1010][1010];
vector<int> e[1010];
//以下为模板匈牙利 
bool dfs(int x){
	if(vis[x]){
		return 0;
	}
	vis[x]=1;
	for(auto v:e[x]){
		if((pp[v]==0)||dfs(pp[v])){
			pp[v]=x;
			return 1;
		}
	}
	return 0;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		getchar();
		for(int j=1;j<=m;j++){
			mp[i][j]=getchar();
		}
	}
	//以下为横向缩点 
	for(int i=1;i<=n;i++){
		int flag=0;
		for(int j=1;j<=m;j++){
			if(mp[i][j]=='o'){
				if(!flag){
					cntx++;
					flag=1;
				}
				x[i][j]=cntx;
			}
			else if(mp[i][j]=='#'){
				flag=0;
			}
		}
	}
	//以下为纵向缩点 
	for(int j=1;j<=m;j++){
		int flag=0;
		for(int i=1;i<=n;i++){
			if(mp[i][j]=='o'){
				if(!flag){
					cnty++;
					flag=1;
				}
				y[i][j]=cnty;
			}
			else if(mp[i][j]=='#'){
				flag=0;
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(x[i][j]&&y[i][j]){
				e[x[i][j]].push_back(y[i][j]);
			}
		}
	}
	for(int i=1;i<=cntx;i++){
		memset(vis,0,sizeof(vis));
		if(dfs(i)){
			ans++;
		}
	}
	cout<<ans;
	return 0;
}

最小点覆盖

定义

在二分图中选择最少的点使得每一条边都有至少一个端点被选中

König 定理

最小点覆盖=最大匹配

算法流程

先做最大匹配，之后每次从左边未匹配的一个点开始去按照：未匹配边->匹配边->未匹配边……的顺序遍历二分图，标记途中经过的点，最小点覆盖为左部点中未被标记的和右部点中被标记的

图示：

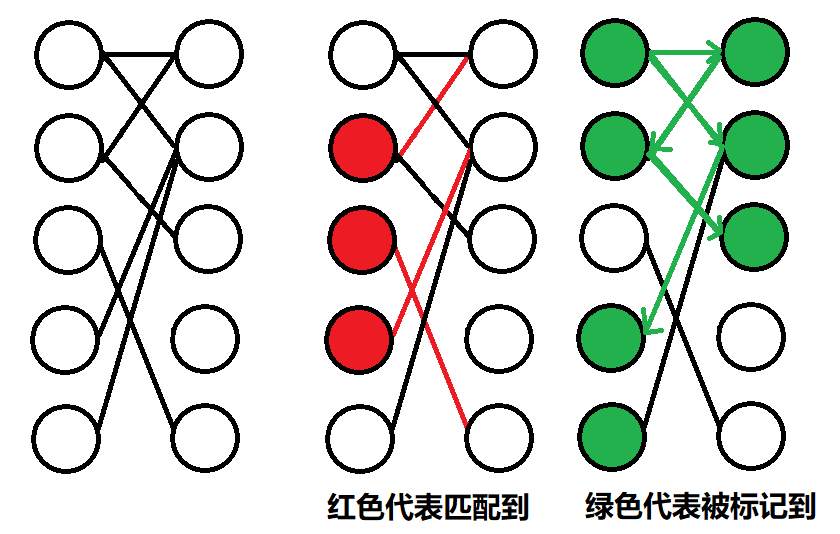
证明：

设选出的点集为 D。

1. D 覆盖了所有边：
   若有一条边左右两端点均不在D集合中，则左端点被标记，右端点未被标记。
   分类讨论：

   • 当当前边被匹配，因为其左部点被标记那么必然是通过右部点来的，则右部点被标记，矛盾。
   • 当当前边未被匹配，因为当前边不是匹配边，所以必然会从左部点出发一次，则右部点被标记，矛盾。
     综上，我们可以知道点集D覆盖了所有边。

2. D 的大小就是最大匹配的点数：

   • 因为每一个左部的非匹配点都会被当起点一次，显然有点集 D 中的左部点是匹配点。
   • 因为若点集 D 中的右部点为非匹配点，那么就可以与来的左部点组成新的匹配，所以点集 D 中的右部点也都是匹配点.
   • 因为左部的匹配点是由右部的匹配点来遍历到的。所以对于一组匹配点，要么两个都被标记，要么都不被标记。
   • 因为上条和选点时是所以，一条匹配边上左侧点和右侧点不可能同时在或者不在点集 D 中
     又因为一条匹配边上左侧点和右侧点不可能同时在或者不在点集 D 中，那么E集合中任意一条边左右两端点中都恰好仅有一个点在点集D中，得证。

3. |D| 是最小的点覆盖数：|D| = 最大匹配数，如果另一个点集的元素个数比|D|更小，那么这个点集必然无法包含所有的匹配边，连所有的匹配边都无法全部包含，怎么可能包含所有边呢。所以|D| 是最小的点覆盖数。