DP入门练习
一、
动态规划(Dynamic Programming,简称 DP)是一种通过分解复杂问题为重叠子问题,并存储子问题的解(避免重复计算) 来高效求解问题的算法思想。它的核心是 “以空间换时间”,适用于具有重叠子问题和最优子结构性质的问题。
-
重叠子问题:问题可以分解为多个重复出现的子问题(例如:计算斐波那契数列时,
fib(5)需要fib(4)和fib(3),而fib(4)又需要fib(3)和fib(2),其中fib(3)被重复计算)。 -
最优子结构:问题的最优解包含子问题的最优解(例如:求 “从 A 到 B 的最短路径”,如果路径 A→C→B 是最优解,那么 A→C 和 C→B 也必须是各自的最短路径)。
二、步骤
- 确定状态:用一个变量(或多个变量)描述问题在某一阶段的 “状态”(即子问题的解)。
- 推导状态转移方程:描述不同状态之间的关系(即如何从已知子问题的解推出当前问题的解)。
- 确定初始条件:最基础的子问题(无法再分解的子问题)的解。
- 计算顺序:通常采用 “自底向上” 的顺序(从基础子问题开始,逐步计算到目标问题),或 “自顶向下 + 记忆化”(递归 + 缓存)。
三、两种实现方式
- 自底向上(递推):
- 从最小的子问题开始计算,逐步推导到目标问题(如斐波那契、爬楼梯)。
- 优点:无递归栈开销,空间可优化,效率高。
- 自顶向下(递归 + 记忆化):
- 直接递归解决目标问题,用哈希表 / 数组缓存子问题的解(避免重复计算)。
- 优点:思路更直观,适合复杂问题。
"递归" 是自顶向下, "递"是分解问题(自顶向下), "归"是计算求解(自底向上); 能不能只有"归"呢? 那就自底向上的 "递推"
递推公式= dfs向下递归的公式, 递推数组初始值= dfs 递归边界(递归搜索树的叶子)
ps:
剪枝 和 记忆化搜索 都是优化dfs的两种方式, 但是要实现剪枝, 就要尽可能多的传递参数(根据参数剪);
但是记忆化搜索, 参数越少越好, 因为记忆化数组需要根据参数来进行映射,(5 个参数可能就需要5维度数组), 这不利于实现.
因此, 在记忆化搜索中, 不应该把没有影响到边界的参数传进来
acwing 5292.跳台阶
一个楼梯共有 n 级台阶,每次可以走一级或两级,问从第 0 级台阶走到第 n 级台阶一共有多少种方案。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示方案数。
数据范围
1≤n≤15
纯dfs暴搜有两种, 一种是从下到上, 一种是从上到下
1. 从下到上:
void solve(){
int n;cin>>n;
int ans=0;
auto f=[&](auto self ,int x)->void{
if(x>n)return;
if(x==n){
ans++;
}else{
self(self,x+1);
self(self,x+2);// 搜索树2个起点? 并非, 其实是0开始
}
};
f(f,0);// 0开始
cout<<ans<<endl;
}
实现记忆化递归 (记忆化一定要递归):
void solve(){
int n;cin>>n;
vector<int> dp(n+1);
auto f=[&](auto self, int x)->int{
if(x>n)return 0; // 代表这条路径不合法
if(x==n)return 1; // 这条路径合法
if(dp[x])return dp[x]; // 记录: 第x层到第n层有多少条路径
int sum = self(self,x+1)+self(self,x+2);// 因为这里要有返回值,所以后面记得return;
dp[x]=sum;
return sum;//
};
f(f,0);
cout<<dp[0]<<endl;
}
直接递推:
刚刚是从 0 搜到 n, 现在要从 n 推回 0
void solve(){
int n;cin>>n;
vector<int> dp(n+1);
dp[n]=1;dp[n-1]=1; // 记录: 第x层到第n层有多少条路径, 所以n层是唯一的, n-1层也是唯一的
for(int i=n-2;i>=0;i--){
dp[i]=dp[i+1]+dp[i+2];
}
cout<<dp[0]<<endl;
}
2. 从上到下:
void solve(){
int n;cin>>n;
auto dfs=[&](auto self , int x)->int{
if(x==1)return 1;
if(x==2)return 2;
return self(self,x-1)+self(self,x-2);
};
cout<<dfs(dfs,n)<<endl; // n开始
}
实现记忆化递归搜索
void solve(){
int n;cin>>n;
vector<int> dp(n+1);
auto dfs=[&](auto self , int x)->int{
if(dp[x])return dp[x];// 如果有记录的话,直接使用记录
int sum=0;
if(x==1)sum=1;
else if(x==2)sum=2;
else sum=self(self,x-1)+self(self,x-2);//用一个sum 来记录当前层的结果
dp[x]=sum;// 第x层的答案为sum, 作为一个映射,用dp数组存下来
return sum;
};
cout<<dfs(dfs,n)<<endl;
}
所以只是存了一下每次递归对应的结果
根据记忆化搜索, 可以很自然地写出递推公式, 这就是最终形态了. (当然这还能用四个变量进一步优化空间, 但这是后话了)
void solve(){
int n;cin>>n;
vector<int> dp(100);
dp[0]=1;dp[1]=1;
if(n>1){
rep(i,2,n){
dp[i]=dp[i-1]+dp[i-2];
}
}
cout<<dp[n]<<endl;
}
Acwing 1049. 大盗阿福
题目描述
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有 N 家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T ,表示一共有 T 组数据。
接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。
第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过 1000 。
输出格式
对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
1 ≤ T ≤ 50 , 1≤N≤10^5
DFS暴搜
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
int ans=0;
vector<int> vis(n+2);
auto f=[&](auto self,int x, int num)->void{
if(x==n+1){
ans=max(ans,num);
}else{
if(vis[x]==0){
vis[x]=1;vis[x+1]=1;
self(self,x+1,num+a[x]);
vis[x]=0;vis[x+1]=0;
self(self,x+1,num);
}else{
self(self,x+1,num);
}
}
};
f(f,1,0);
cout<<ans<<endl;
}
注意到这里的num 参数不是影响边界的条件, 理论上来说适合剪枝优化 而不是 记忆化或者说dp
那不妨先剪个枝吧, 可以是当前的num加上后续所有的 a[x]如果还小于ans就直接return, 但是这样感觉优化不了多少, 我暂时想不到更好的剪枝了
首先可以优化掉vis数组, 转变为如果选了当前的x, 就考虑x+2,否则考虑x+1, 那搜索树也很直观了, 先画出来吧,
auto f=[&](auto self,int x, int num)->void{
if(x>n){// x>n
ans=max(ans,num);
}else{
self(self,x+2,num+a[x]);
self(self,x+1,num);
}
};
能不能再优化掉这个不决定边界的参数num ?
现在就先 "递" 搜索选择方案, 然后 " 归 "计算局部最优解 ?
现在用dp数组记录到第x个时, 选或不选 a[x] 的最优解, 最优解表示为 max( f(x+1), a[x] + f(x+2) ) 这个要根据搜索树写出来
最小子问题呢? 应该是 到第n层 的时候 , 不能再往下了, 那就把它选进来 或者到第 n-1 的时候, 肯定不能选n (相邻) 或者n+1了(n+1根本不存在)
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
int ans=0;
vector<int> dp((int)1e5+5);
auto f=[&](auto self,int x)->int{
if(x>n)return 0;//可有可无好像是
if(dp[x])return dp[x];
if(x==n)return a[n];
if(x==n-1)return max(a[n-1],a[n]);
// 选的话就是加上a[n-1],然后不能再选下一个a[n]了(至于a[n-2]呢?如果选了a[n-2],根本就不会进入到n-1这层考虑)
int sum = max(self(self,x+1), self(self,x+2)+a[x] ); // 当前层的最优解记为sum;
dp[x]=sum;
return sum;
};
f(f,1);
cout<<dp[1]<<endl;
}
然后写递推
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
vector<int> dp((int)1e5+5);
dp[n]=a[n];dp[n-1]=max(a[n-1],a[n]);
for(int i=n-2;i>=1;i--){
dp[i]=max(dp[i+1],dp[i+2]+a[i]);
}
cout<<dp[1]<<endl;
}
P1216 [IOI 1994] 数字三角形 Number Triangles
题目描述
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
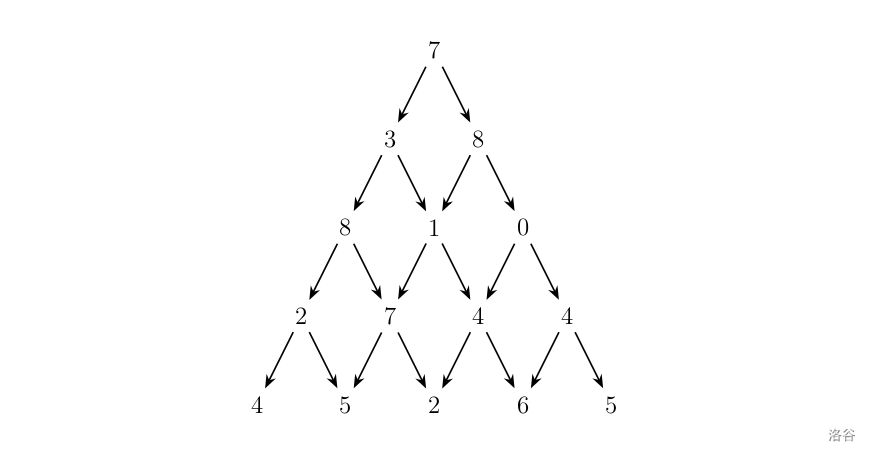
在上面的样例中,从 7→3→8→7→5 的路径产生了最大权值。
输入格式
第一个行一个正整数 r,表示行的数目。1≤r≤1000
后面每行为这个数字金字塔特定行包含的整数 [0,100] 。
输出格式
单独的一行,包含那个可能得到的最大的和。
输入输出样例
输入 #1复制
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出 #1复制
30
和上一题类似,对于每个节点, 都记录走这条节点往下的最大值
那么, 走当前节点(x,y)的 最优解(最大值) 就是 dp[x][y] = a[x][y] + max( dp[x+1][y] , dp[x+1][y+1] )
最小子问题就是最下面那层 dp [n] [i] = a [n] [i] ;
然后就从下往上递推回去
void solve(){
int n;cin>>n;
vector<vector<int>> a(1001,vector<int>(1001));
vector<vector<int>> dp(1001,vector<int>(1001));
rep(i,1,n){
rep(j,1,i){
cin>>a[i][j];
}
}
rep(i,1,n)dp[n][i]=a[n][i];
for(int i=n-1;i>=1;i--){
for(int j=1;j<=i;j++){
dp[i][j]=a[i][j]+max(dp[i+1][j],dp[i+1][j+1]);
}
}
cout<<dp[1][1]<<endl;
}
那现在能不能还原递归搜索树呢?
auto f=[&](auto self, int x,int y)->int{
if(dp[x][y])return dp[x][y];// dp数组是二维的,显然需要两个决定边界的参数
int sum = a[x][y]+max(self(self,x+1,y),self(self,x+1,y+1));
dp[x][y]=sum; // 别忘了记录
return sum;
};
f(f,1,1);
但是 RE 了, 所以之后的这种题用递推来做吧...
Acwing 01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
先不管什么记忆化或者dp了, 从朴素的来看, 这就是一个指数型枚举
然后就可以顺手写个暴搜
void solve(){
int n,m;cin>>n>>m;
vector<pair<int,int>> a(n+1);
rep(i,1,n){
int v,w;cin>>v>>w;
a[i].first=v;a[i].second=w;
}
int ans=0;
auto f=[&](auto self,int x, int sp ,int sum)->void{
if(x>n){
ans=max(ans,sum);
} else{
// if(sp>=a[x].first){
// self(self,x+1,sp-a[x].first,sum+a[x].second);
// self(self,x+1,sp,sum);
// }else{
// self(self,x+1,sp,sum);
// }
//这写的太复杂了, 这样就好↓
if(sp>=a[x].first){
self(self,x+1,sp-a[x].first,sum+a[x].second);
}
self(self,x+1,sp,sum);//无论如何都保留不选
}
};
f(f,1,m,0);
cout<<ans<<endl;
}
选到第 x 件物品和背包的剩余容量 sp 都会影响搜索树的边界, 那 dp 数组自然就要开二维的,
(记忆化一定是有用的, 比如通过前面的某一些选法, 到了这一件物品或者说这一层, 都剩余这么多空间 , 这么多空间就有一个使价值最大化的解(利用方案, 如果之前搜过, 那就直接使用 ) , 然后利用这个后面的最优解, 去尝试(chose or not )和计算上面一层的解. ) (这里前面描述的是"递", 后面遇到已知最优解是"归")
x和 sp 肯定要在搜索树中保留, 然后优化掉 sum, 也就是: 先只走路, 画搜索树
对于第一个点(1,m), f(f,1,m,0);也是从(1,m)开始搜嘛,这很合理
这个状态表示: 对第一件物品, 还剩余m 的空间
那么如果取第一件物品 搜索树就会有 : (1,m) → ( 2 , m - a[1].v )
如果不选的话就是 : (1,m) → ( 2 , m )
那么当前层的答案就是: max( f(2,m), a[1].w+f(2,m-a[1].v) ) ?
dp[ x ] [ y ] 存的是当前最优解
差点忘记分析搜索树底了...
如果到了最底层还有剩余足够的空间, 那一定要把这个选上
发现都只要考虑下一层, 那就只考虑x==n的时候了
void solve(){
int n,m;cin>>n>>m;
vector<pair<int,int>> a(n+1);
rep(i,1,n){
int v,w;cin>>v>>w;
a[i].first=v;a[i].second=w;
}
vector<vector<int>> dp(n+1,vector<int> (m+1,-1));//
auto f=[&](auto self,int x, int sp )->int{
// if(sp<0)return -a[x-1].second;// 返回负数, 不能返回0 ? (因为返回的是 a[x].second+self(self,x+1,sp-a[x].first), 要使得这个为0 )
// 或者别这样写了↑ ,这样也不利于写递推公式
if(dp[x][sp]>-1)return dp[x][sp];
if(x==n){
// if(sp>=a[n].first)return a[n].second;// 剩余空间放得下一定要放
// return 0; // 放不下了肯这个局部解只能是0
if(sp>=a[n].first){
dp[n][sp]=a[n].second; return dp[n][sp];
}else{
dp[n][sp]=0;
return dp[n][sp];
}
}
int sum ;
if(sp>=a[x].first){
sum = max( self(self,x+1,sp), a[x].second+self(self,x+1,sp-a[x].first) );
}else{
sum = self(self,x+1,sp);
}
dp[x][sp]=sum;
return dp[x][sp];
};
f(f,1,m);
cout<<dp[1][m]<<endl;
}
现在从下往还上推回去
void solve(){
int n,m;cin>>n>>m;
vector<pair<int,int>> a(n+1);
rep(i,1,n){
int v,w;cin>>v>>w;
a[i].first=v;a[i].second=w;
}
vector<vector<int>> dp(n+1,vector<int> (m+1));
rep(sp,1,m){
if(sp<a[n].first)dp[n][sp]=0;
else dp[n][sp]=a[n].second;
}
for(int i=n-1;i>=1;i--){
for(int j=1;j<=m;j++){
if(j>=a[i].first)dp[i][j]=max( dp[i+1][j], a[i].second+dp[i+1][j-a[i].first] );
else dp[i][j]=dp[i+1][j];
}
}
cout<<dp[1][m]<<endl;
}
perfect!!!
Acwing 二维费用的背包问题
有 N 件物品和一个容量是 V 的背包,背包能承受的最大重量是 M。
每件物品只能用一次。体积是 vi,重量是 mi,价值是 wi。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
输入格式
第一行三个整数,N,V,M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N 行,每行三个整数 vi,mi,wi,用空格隔开,分别表示第 i 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V,M≤100
0<vi,mi≤100
0<wi≤1000
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例:
8
void solve(){
int n,v,m;cin>>n>>v>>m;
struct file{
int v,m,w;
};
vector<file> a(n+1);
rep(i,1,n){
int v,m,w;cin>>v>>m>>w;
a[i].v=v;a[i].m=m;a[i].w=w;
}
vector<vector<vector<int>>> dp(n+1,vector<vector<int>>(v+1,vector<int>(m+1,-1)));
auto f=[&](auto self , int x, int spv , int spm)->int{
if(dp[x][spv][spm]!=-1)return dp[x][spv][spm]; // 不能是if(dp[x][spv][spm])return, 否则超时
if(x==n){
if(spv>=a[n].v && spm>=a[n].m){
return dp[x][spv][spm]=a[n].w;
}else{
return dp[x][spv][spm]=0;
}
}
int sum ;
if(spv>=a[x].v && spm>=a[x].m){
sum=max( self(self,x+1,spv,spm) , a[x].w + self(self, x+1,spv-a[x].v,spm-a[x].m));
}else{
sum=self(self,x+1,spv,spm);
}
dp[x][spv][spm]=sum;
return sum;
};
f(f,1,v,m);
cout<<dp[1][v][m]<<endl;
}
不能是if(dp[x][spv][spm])return; ?
dp数组初始值为0,而很多有效状态的最大价值本身就可能是0(例如:选不了任何物品时)。- 当某个状态的最大价值为
0时,dp[x][spv][spm]会被赋值为0,但下次访问该状态时,if(dp[...])会判定为false(因为0为假),导致该状态被重复计算。
那建议以后未访问的都设为-1
Acwing 完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10
void solve(){
int n,m;cin>>n>>m;
vector<pair<int,int>> a(n+1);
rep(i,1,n){
int v,w;cin>>v>>w;
a[i].first=v;a[i].second=w;
}
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
auto f = [&](auto self, int x, int sp)->int{
if(dp[x][sp]>-1){
return dp[x][sp];
}
if(x==n){
int sum = 0;
int tem_sp=sp;
while(tem_sp>=a[n].first){ // 不是sp>0, 要大于最后一个物品的大小
sum+=a[n].second;
tem_sp-=a[n].first;
}
return dp[x][sp]=sum;//
}
int sum;
if(sp>=a[x].first){
sum = max(a[x].second+self(self,x,sp-a[x].first),self(self,x+1,sp));
}else{
sum = self(self,x+1,sp);
}
dp[x][sp]=sum;//
return sum;//
};
f(f,1,m);
cout<<dp[1][m]<<endl;
}
直到做到这里才猛然回头发现前面的一些记忆化搜索写的并不规范: 在处理边界的时候, 会漏掉一些对 边界 dp数组 赋值的情况 ( 导致如果层数x 只有1, 那么输出的dp数组就变成-1了) 所以建议return 都return dp [x] [sp] = ...;
写个递推吧
void solve(){
int n,m;cin>>n>>m;
vector<pair<int,int>> a(n+1);
rep(i,1,n){
int v,w;cin>>v>>w;
a[i].first=v;a[i].second=w;
}
vector<vector<int>> dp(n+1,vector<int>(m+1));// 不用初始化 -1 了
rep(sp,1,m){ // 1~m
dp[n][sp]+=(sp/a[n].first)*a[n].second;
}
for(int i=n-1;i>=1;i--){
for(int j=1;j<=m;j++){
if(j>=a[i].first){
dp[i][j]=max(a[i].second+dp[i][j-a[i].first],dp[i+1][j]);
}else{
dp[i][j]=dp[i+1][j];
}
}
}
cout<<dp[1][m]<<endl;
}
P10955 正整数拆分
题目描述
给定一个正整数 N,要求把 N 拆分成若干个正整数相加的形式,参与加法运算的数可以重复。
注意:
- 拆分方案不考虑顺序;
- 至少拆分成 2 个数的和。
求拆分的方案数 mod 2147483648 的结果。
emmmm这题就是一个完全背包题, n为空间, 每个数的大小为每个物品空间, 物品价值都为0 但是要算有多少种装法
dp[x] [ sp ] 记录选 到第x 个数, 还余下多少"空间"
如果能选 x : 接下来要计算的是 dp [ x ] [sp- x]
如果不选了 : 计算的是 dp [x+1], [sp]
如果不能选: 计算 dp [x ] [ sp ]
所以, dp[ x] [ sp ] = dp [ x ] [sp- x] + dp [x+1] [sp]
void solve(){
int n;cin>>n;
int mod=2147483648;
vector<vector<int>> dp(n+1,vector<int>(n+1,-1));
auto f=[&](auto self, int x ,int sp)->int{
if(x==n)return dp[x][sp]=0;
if(sp<x)return dp[x][sp]=0;
if(dp[x][sp]>-1)return dp[x][sp];
if(sp==x)return dp[x][sp]=1;
// 现在一定sp>x;
int sum=0;
sum = (self(self,x,sp-x)%mod+self(self,x+1,sp)%mod)%mod;
return dp[x][sp]=sum;
};
f(f,1,n);
cout<<dp[1][n]<<endl;
}
Leetcode 343. 整数拆分
给定一个正整数n (2<=n<=58), 将其拆分为k ( k>=2 ) 个正整数的和, 并使这些整数的乘积最大化
输出最大化的乘积
和上一题类似
dp[ x ] [ sp ] 表示选到第 x个数且剩余空间为sp时的 最大化的乘积
dp [ x ] [ sp ] = max( chose: x*dp[ x] [ sp ] , not chose: dp [ x ] [ sp ])
void solve(){
int n;cin>>n;
vector<vector<int>> dp(n+1,vector<int>(n+1,-1));
auto f=[&](auto self, int x ,int sp)->int{
if(x==n)return dp[x][sp]=0;
if(sp<x)return dp[x][sp]=0;//都是不合法的拆分方案
if(dp[x][sp]>-1)return dp[x][sp];
if(sp==x)return dp[x][sp]=x;
int sum = max( x*self(self,x,sp-x), self(self,x+1,sp));
return dp[x][sp]=sum;
};
f(f,1,n);
cout<<dp[1][n]<<endl;
}
B3637 最长上升子序列
题目描述
给出一个由 n(n≤5000) 个不超过 106 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。
最长上升子序列是指,从原序列中按顺序取出一些数字排在一起,这些数字是逐渐增大的。
输入格式
第一行,一个整数 n,表示序列长度。第二行有 n 个整数,表示这个序列。
输出格式
一个整数表示答案。
输入输出样例
输入 #1
6
1 2 4 1 3 4
输出 #1
4
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
vector<int> dp(n+1,-1); // 表示以a[x]开头的最长上升子序列长度!!!!!!!!!!!
auto f=[&](auto self,int x)->int{
if(dp[x]>-1)return dp[x];
int len=1;
for(int i=x+1;i<=n;i++){
if(a[x]<a[i]){
len= max ( len, self(self,i)+1 ) ; // 扫一遍更新, 递归更新
}
}
return dp[x]=len;
};
int ans=0;
rep(i,1,n){
ans=max(ans,f(f,i));// 答案并不一定是a[1]开头的dp[1], 所以要把每个都开头都调用一遍函数, 反正有记忆化
}
cout<<ans<<endl;
}
B4133 [信息与未来 2014] 最大连续部分(子段)和
题目描述
有 n 个整数排成一排,求其中的最大连续部分和。
至少要选一个数。
输入格式
第一行一个整数,表示 n。
第二行 n 个整数 x1,x2,⋯,xn,相邻两数之间有一个空格。1≤n≤107,0≤∣xi∣≤108。
输出格式
一个整数(即最大的连续的部分和)。
输入输出样例
输入 #1
7
-2 13 12 9 14 -10 2
输出 #1
48
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
// 每个数都有可能是开头,
vector<int> dp(n+1,-1); // 以a[x]开头的最大子段和
auto f=[&](auto self, int x)->int{
if(dp[x]>-1)return dp[x];
if(x==n){
dp[n]=a[n];return dp[n];
}
int sum=a[x];
sum = max(sum, a[x]+self(self,x+1));
return dp[x]=sum;
};
int ans=-1e9;
rep(i,1,n){
ans=max(ans,f(f,i));
}
cout<<ans<<endl;
}
但是这样有一个测试点MLE了
写递推?
void solve(){
int n;cin>>n;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
vector<int> dp(n+1);
dp[n]=a[n];
for(int i =n-1;i>=1;i--){
dp[i]=max(a[i],a[i]+dp[i+1]);
}
int ans=-1e9;
rep(i,1,n)ans=max(ans,dp[i]);
cout<<ans<<endl;
}
成功AC



 浙公网安备 33010602011771号
浙公网安备 33010602011771号