DFS练习
关于DFS的入门练习题的一些题解 (题目节选自b站一只会code的小金鱼)
基础三件套: 递归实现 指数枚举, 组合枚举, 排列枚举
递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define endl '\n'
#define int long long
const int N=2e5+5;
void solve(){
int n;cin>>n;
vector<int>v;
auto f=[&](this auto && self,int x)->void {
if(x==n+1){
for(auto &i:v){
cout<<i<<' ';
}
cout<<endl;
}else{
v.push_back(x) ;
self(x+1);
v.pop_back();
self(x+1);
}
};
f(1);
}
signed main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//int _;cin>>_;while(_--)
solve();
return 0;
}
ps: 这里的 lambda 函数递归采用c++23风格, 之后会使用更通用的c++14风格. 之后的代码非必要只贴出solve()部分.
递归实现组合型枚举
从 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。
void solve(){
int n,m;cin>>n>>m;
vector<int> v;
auto f=[&](auto self,int x)->void {
if(v.size()>m||v.size()+n-x+1<m)return;
if(x==n+1){
for(int &i:v){
cout<<i<<' ';
}cout<<endl;
}else{
//chose or not
v.push_back(x);
self(self,x+1);
v.pop_back();
self(self,x+1);
}
};
f(f,1);
}
递归实现排列型枚举
把 1∼n 这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
void solve(){
int n; cin>>n;
vector<int> v;
vector<int> vis(n+1);
auto f=[&](auto self,int x)->void {
if(x==n+1){
for(int i:v){
cout<<i<<' ';
}cout<<endl;
}else{
for(int i=1;i<=n;i++){
if(vis[i]==0){
vis[i]=1;
v.push_back(i);
self(self,x+1);
v.pop_back();
vis[i]=0;
}
}
}
};
f(f,1);
}
洛谷 P1036 [NOIP 2002 普及组] 选数
已知 n 个整数 x1,x2,⋯,xn,以及 1 个整数 k(k<n)。从 n 个整数中任选 k 个整数相加,可分别得到一系列的和。例如当 n=4,k=3,4 个整数分别为 3,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29。
void solve(){
int n,k;cin>>n>>k;
vector<int> a(n+1);
rep(i,1,n){
cin>>a[i];
}
vector<int> v;
int ans=0;
auto isprime =[&](int num)->bool{
if(num==1)return 0;
int ok=1;
for(int i=2;i*i<=num;i++){
if(num%i==0){
ok=0;break;
}
}
return ok;
};
auto f=[&](auto && self,int x)->void {
if(v.size()>k||v.size()+(n-x+1)<k)return ;
if(x==n+1){
int sum=0;
for(auto &j:v){
sum+=j;
}
if(isprime(sum)){
ans++;
}
}else{
v.push_back(a[x]);
self(self,x+1);
v.pop_back();
self(self,x+1);
}
};
f(f,1);
cout<<ans<<endl;
}
洛谷 P2089 烤鸡
猪猪 Hanke 特别喜欢吃烤鸡(本是同畜牲,相煎何太急!)Hanke 吃鸡很特别,为什么特别呢?因为他有 10 种配料(芥末、孜然等),每种配料可以放 1 到 3 克,任意烤鸡的美味程度为所有配料质量之和。
现在, Hanke 想要知道,如果给你一个美味程度 n ,请输出这 10 种配料的所有搭配方案。
void solve(){
int n;cin>>n;
vector<int> v;
vector<int> ans;
auto f=[&](auto &&self , int x, int sum)->void{
if(sum>n)return ;
if(x==11){
if(sum<n)return ;
for(auto &i:v){
ans.push_back(i);
}
}else{
rep(i,1,3){
v.push_back(i);
self(self,x+1,sum+i);
v.pop_back();
}
}
};
f(f,1,0);
cout<<ans.size()/10<<endl;
rep(i,1,ans.size()/10){
rep(j,0,9){
cout<<ans[(i-1)*10+j]<<' ';
}cout<<endl;
}
}
洛谷 P1088 [NOIP 2004 普及组] 火星人
人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言,但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的,首先,火星人把一个非常大的数字告诉人类科学家,科学家破解这个数字的含义后,再把一个很小的数字加到这个大数上面,把结果告诉火星人,作为人类的回答。
火星人用一种非常简单的方式来表示数字――掰手指。火星人只有一只手,但这只手上有成千上万的手指,这些手指排成一列,分别编号为 1,2,3,⋯。火星人的任意两根手指都能随意交换位置,他们就是通过这方法计数的。
一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指――拇指、食指、中指、无名指和小指分别编号为 1,2,3,4 和 5,当它们按正常顺序排列时,形成了 5 位数 12345,当你交换无名指和小指的位置时,会形成 5 位数 12354,当你把五个手指的顺序完全颠倒时,会形成 54321,在所有能够形成的 120 个 5 位数中,12345 最小,它表示 1;12354 第二小,它表示 2;54321 最大,它表示 120。下表展示了只有 3 根手指时能够形成的 6 个 3 位数和它们代表的数字:
| 三位数 | 代表的数字 |
|---|---|
| 123 | 1 |
| 132 | 2 |
| 213 | 3 |
| 231 | 4 |
| 312 | 5 |
| 321 | 6 |
现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指,科学家会告诉你要加上去的很小的数。你的任务是,把火星人用手指表示的数与科学家告诉你的数相加,并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。
void solve(){
int n,m;
cin>>n>>m;
vector<int> a(n+1);
rep(i,1,n)cin>>a[i];
rep(i,1,m)next_permutation(a.begin()+1,a.end()); // 这里使用了全排列的stl,
// 但并不意味着全排列问题都可以用 stl 解决了,
//有全排列思想的题目还是需要自己手搓, 后面有一题也会涉及
rep(i,1,n)cout<<a[i]<<' ';
cout<<endl;
}
洛谷P1149 [NOIP 2008 提高组] 火柴棒等式
给你 n 根火柴棍,你可以拼出多少个形如 A+B=C 的等式?等式中的 A、B、C 是用火柴棍拼出的整数(若该数非零,则最高位不能是 0)。用火柴棍拼数字 0∼9 的拼法如图所示:
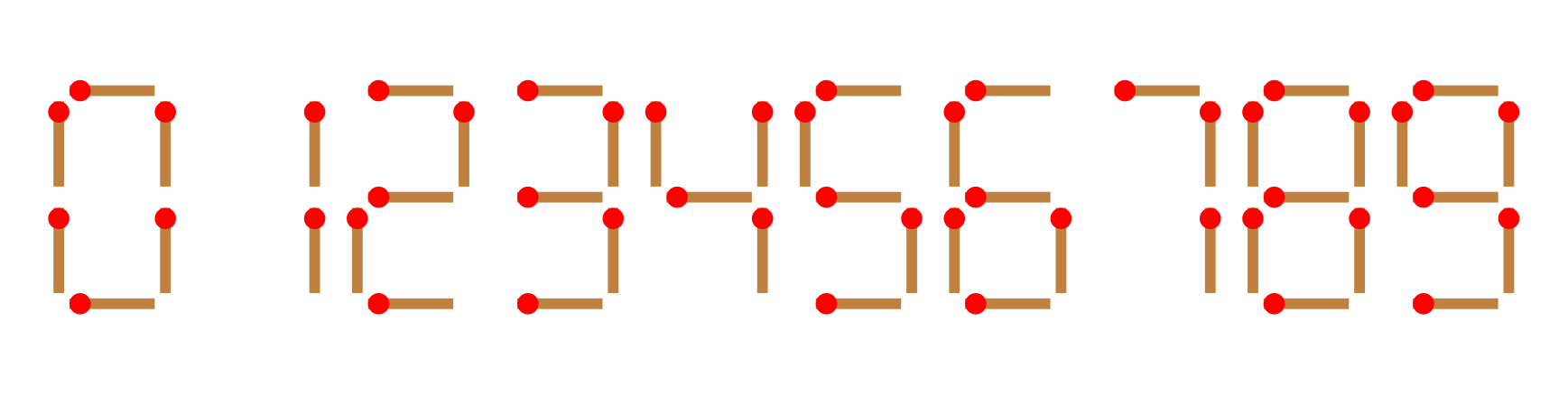
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 A!=B,则 A+B=C 与 B+A=C 视为不同的等式(A,B,C≥0);
- n 根火柴棍必须全部用上。
void solve(){
int n;cin>>n;
vector<int> v{6,2,5,5,4,5,6,3,7,6};
int ans=0;
vector<int> a(5);
auto cal=[&](int x){
int ans=0;
while(x>=10){
ans+=v[x%10];
x/=10;
}
ans+=v[x];
return ans;
};
auto f=[&]( auto &&self ,int x,int sum)->void {
if(sum>n)return ;
if(x==4){
if(a[1]+a[2]==a[3] && sum==n-4){
ans++;
}
return ;
}
rep(i,0,1000){
a[x]=i;
self(self,x+1,sum+cal(a[x]));
}
};
f(f,1,0);
cout<<ans<<endl;
}
洛谷 P2036 [COCI 2008/2009 #2] PERKET
Perket 是一种流行的美食。为了做好 Perket,厨师必须谨慎选择食材,以在保持传统风味的同时尽可能获得最全面的味道。你有 n 种可支配的配料。对于每一种配料,我们知道它们各自的酸度 s 和苦度 b。当我们添加配料时,总的酸度为每一种配料的酸度总乘积;总的苦度为每一种配料的苦度的总和。
众所周知,美食应该做到口感适中,所以我们希望选取配料,以使得酸度和苦度的绝对差最小。
另外,我们必须添加至少一种配料,因为没有任何食物以水为配料的。
void solve(){
int n;cin>>n;
vector<pair<int,int>> a;
rep(i,1,n){
int x,y ;cin>>x>>y;
a.push_back({x,y});
}
int mi=1e9+1;
vector<pair<int,int>> v;
auto f=[&](auto &&self ,int x)->void{
if(x==n){
if(v.empty())return ;
int suan=1;int ku=0;
for(auto &[p,q]:v){
suan*=p;
ku+=q;
}
mi=min(mi,abs(suan-ku));
}else{
v.push_back(a[x]);
self(self,x+1);
v.pop_back();
self(self,x+1);
}
};
f(f,0);
cout<<mi<<endl;
}
洛谷 P1135 奇怪的电梯
大楼的每一层楼都可以停电梯,而且第 i 层楼(1≤i≤N)上有一个数字 K**i(0≤K**i≤N)。电梯只有四个按钮:开,关,上,下。上下的层数等于当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如: 3,3,1,2,5 代表了 K**i(K1=3,K2=3,……),从 1 楼开始。在 1 楼,按“上”可以到 4 楼,按“下”是不起作用的,因为没有 −2 楼。那么,从 A 楼到 B 楼至少要按几次按钮呢?
(本题使用 dfs 解法只会通过部分测试点,正解应该采用 bfs )
void solve(){
int n,a,b;
cin>>n>>a>>b;
vector<int> v(n+1);
rep(i,1,n)cin>>v[i];
int ans=1e18;
vector<int> vis(205);
auto f=[&](auto self , int cur,int cnt)->void {
if(cur==b){
ans=min(ans,cnt);
}else{
if(cur + v[cur] <= n && vis[cur + v[cur] ]==0){
vis[cur + v[cur] ]=1;
self(self,cur + v[cur],cnt+1);
vis[cur + v[cur] ]=0;
}
if(cur- v[cur]>=1 && vis[cur - v[cur] ]==0){
vis[cur - v[cur] ]=1;
self(self,cur - v[cur],cnt+1);
vis[cur - v[cur] ]=0;
}
}
};
f(f,a,0);
if(ans!=1e18)cout<<ans<<endl;
else cout<<-1<<endl;
}
洛谷 P1683 入门 (迷宫类问题入门)
题目描述
不是任何人都可以进入桃花岛的,黄药师最讨厌像郭靖一样呆头呆脑的人。所以,他在桃花岛的唯一入口处修了一条小路,这条小路全部用正方形瓷砖铺设而成。有的瓷砖可以踩,我们认为是安全的,而有的瓷砖一踩上去就会有喷出要命的毒气,那你就死翘翘了,我们认为是不安全的。你只能从一块安全的瓷砖上走到与他相邻的四块瓷砖中的任何一个上,但它也必须是安全的才行。
由于你是黄蓉的朋友,她事先告诉你哪些砖是安全的、哪些砖是不安全的,并且她会指引你飞到第一块砖上(第一块砖可能在任意安全位置),现在她告诉你进入桃花岛的秘密就是:如果你能走过最多的瓷砖并且没有死,那么桃花岛的大门就会自动打开了,你就可以从当前位置直接飞进大门了。
注意:瓷砖可以重复走过,但不能重复计数。
输入格式
第一行两个正整数 W 和 H,分别表示小路的宽度和长度。
以下 H 行为一个 H×W 的字符矩阵。每一个字符代表一块瓷砖。其中,. 代表安全的砖,# 代表不安全的砖,@ 代表第一块砖。
输出格式
输出一行,只包括一个数,即你从第一块砖开始所能安全走过的最多的砖块个数(包括第一块砖)。
/*
起始点处理:在找到起始点@后,立即将其标记为已访问并计数,然后开始 DFS。
地图索引调整:将地图的存储和访问方式从 1-based 改为 0-based,与输入字符串的索引方式一致。
*/
void solve(){
int m,n;cin>>m>>n;
vector<string> g(n+1);
rep(i,1,n)cin>>g[i];
rep(i,1,n)g[i]=' '+g[i];
auto inmap=[&](int x,int y){
if(x>=1&&x<=n&&y>=1&&y<=m)return 1;
return 0;
};
int dx[]={1,-1,0,0};
int dy[]={0,0,1,-1};
int ans=1;
vector<vector<int>> vis(n+1,vector<int>(m+1));
auto f=[&](auto self ,int x,int y)->void{
rep(i,0,3){
int u=x+dx[i];
int v=y+dy[i];
if(inmap(u,v) && g[u][v]=='.'&& vis[u][v] == 0){
vis[u][v]=1;
ans++;
self(self,u,v);
}
}
};
rep(i,1,n){
rep(j,1,m){
if(g[i][j]=='@'){
vis[i][j]=1;
f(f,i,j);
}
}
}
cout<<ans<<endl;
}
洛谷 P1605 迷宫
题目描述
给定一个 N×M 方格的迷宫,迷宫里有 T 处障碍,障碍处不可通过。
在迷宫中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
给定起点坐标和终点坐标,每个方格最多经过一次,问有多少种从起点坐标到终点坐标的方案。
输入格式
第一行为三个正整数 N,M,T,分别表示迷宫的长宽和障碍总数。
第二行为四个正整数 SX,S**Y,FX,F**Y,SX,S**Y 代表起点坐标,FX,F**Y 代表终点坐标。
接下来 T 行,每行两个正整数,表示障碍点的坐标。
输出格式
输出从起点坐标到终点坐标的方案总数。
void solve(){
int n,m,t;cin>>n>>m>>t;
vector<vector<int>> vis(n+1,vector<int> (m+1));
int sx,sy,fx,fy;cin>>sx>>sy>>fx>>fy;
vis[sx][sy]=1;//!!!!!!!!!!!!!!!!!!!!
rep(i,1,t){
int x,y;cin>>x>>y;
vis[x][y]=1;
}
auto inmap=[&](int x, int y){
if(x>=1&&x<=n&&y>=1&&y<=m)return 1;
return 0;
};
int ans=0;
int dx[]={1,-1,0,0};
int dy[]={0,0,1,-1};
auto f=[&](auto self ,int x,int y)->void {
if(x==fx&&y==fy){
ans++;return;
}else{
rep(i,0,3){
int u=x+dx[i];
int v=y+dy[i];
if(inmap(u,v) && vis[u][v]==0){
vis[u][v]=1;
self (self ,u,v);
vis[u][v]=0;
}
}
}
};
f(f,sx,sy);
cout<<ans<<endl;
}
洛谷 P1596 [USACO10OCT] Lake Counting S
题目描述
由于最近的降雨,水在农夫约翰的田地里积聚了。田地可以表示为一个 N×M 的矩形(1≤N≤100;1≤M≤100)。每个方格中要么是水(W),要么是干地(.)。农夫约翰想要弄清楚他的田地里形成了多少个水塘。一个水塘是由连通的水方格组成的,其中一个方格被认为与它的八个邻居相邻。给定农夫约翰田地的示意图,确定他有多少个水塘。
输入格式
第 1 行:两个用空格分隔的整数:N 和 M。
第 2 行到第 N+1 行:每行 M 个字符,表示农夫约翰田地的一行。
每个字符要么是 W,要么是 .。
字符之间没有空格。
输出格式
第 1 行:农夫约翰田地中的水塘数量。
void solve(){
int m,n;cin>>n>>m;
vector<string> g(n+1);
rep(i,1,n)cin>>g[i];
rep(i,1,n)g[i]=' '+g[i];
int dx[]={1,-1,0,0,1,1,-1,-1};
int dy[]={0,0,1,-1,1,-1,1,-1};
vector<vector<int>> vis(n+1,vector<int>(m+1));
auto inmap=[&](int x,int y){
if(x>=1&&x<=n&&y>=1&&y<=m)return 1;
return 0;
};
int ans=0;
auto f=[&](auto self ,int x,int y)->void{
rep(i,0,7){
int u=x+dx[i];
int v=y+dy[i];
if(inmap(u,v) && g[u][v]=='W'&& vis[u][v] == 0){
vis[u][v]=1;
self(self,u,v);
}
}
};
rep(i,1,n){
rep(j,1,m){
if(g[i][j]=='W'&& vis[i][j]==0){
ans++;
f(f,i,j);
}
}
}
cout<<ans<<endl;
}
acwing1114 棋盘问题
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。
要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放 k 个棋子的所有可行的摆放方案数目 C。
输入格式
输入含有多组测试数据。
每组数据的第一行是两个正整数 n,k,用一个空格隔开,表示了将在一个 n∗n 的矩阵内描述棋盘,以及摆放棋子的数目。当为-1 -1时表示输入结束。
随后的 n 行描述了棋盘的形状:每行有 n 个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
输出格式
对于每一组数据,给出一行输出,输出摆放的方案数目 C 数据保证 C<2^31)。
数据范围 n≤8,k≤n
void solve(){
int n,k;cin>>n>>k;
while(n!=-1){
vector<string> g(n+1);
rep(i,1,n)cin>>g[i];
rep(i,1,n)g[i]=' '+g[i];
vector<int> vis(n+1);
int ans=0;
auto f=[&](auto self , int p, int cnt )->void{
if(p==n+1){
if(cnt==k)ans++;
return ;
}else{
rep(i,1,n){
if(g[p][i]=='#'&&vis[i]==0){
vis[i]=1;
self(self,p+1,cnt+1);
vis[i]=0;
//self(self,p+1,cnt);
}
}
self(self,p+1,cnt);
}
};
f(f,1,0);
cout<<ans<<endl;
cin>>n>>k;
}
}
洛谷 P1219 [USACO1.5] 八皇后 Checker Challenge
题目描述
一个如下的 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
输入格式
一行一个正整数 n,表示棋盘是 n×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
/*
对角线标记映射的原理
在棋盘上,每个格子 (p, i) (p 是行号,i 是列号)可以通过两个关键公式映射到对应的对角线上:
主对角线(左上到右下)的映射:
对于同一条主对角线上的所有格子,它们的 列号减去行号(i - p) 是恒定的。例如:
格子 (1,2) 和 (2,3) 都在同一条主对角线上,它们的 i - p 都是 1。
由于 i - p 可能为负数(例如格子 (2,1) 的 i - p = -1),而数组索引不能为负,所以代码中使用 n - i + p 来保证结果为正数。
副对角线(右上到左下)的映射:
对于同一条副对角线上的所有格子,它们的 列号加行号(i + p) 是恒定的。例如:
格子 (1,6) 和 (2,5) 都在同一条副对角线上,它们的 i + p 都是 7。
这个值的范围是 2 到 2n,所以直接使用 i + p 作为数组索引即可。
为什么这两个映射是正确的?
唯一性:每个格子 (p, i) 计算出的 n - i + p 和 i + p 都是唯一的,确保不会与其他格子冲突。
对角线覆盖:
所有在同一条主对角线上的格子,其 n - i + p 值相同。
所有在同一条副对角线上的格子,其 i + p 值相同。
互不干扰:主对角线和副对角线的映射公式不同,因此不会互相干扰。
*/
void solve(){
int n;cin>>n;
vector<int> vis(n+1);
vector<int> vis2(n*2);
vector<int> vis3(n*2);
vector<int> v;
int cnt=0;
int ans=0;
auto f=[&](auto self ,int p)->void {
if(p==n+1){
ans++;
if(cnt<=2){
for(auto &i:v){
cout<<i<<" ";
}
cout<<endl;
cnt++;
}
}else{
rep(i,1,n){
if(vis[i]==0&& vis2[n-i+p]==0 &&vis3[i+p]==0){
//不合法的放置所有的行和列 会导致进入不了这个if ,
//导致到不了n+1就被终止递归
vis[i]=1;vis2[n-i+p]=1;vis3[i+p]=1;
v.push_back(i);
self(self,p+1);
vis[i]=0;vis2[n-i+p]=0;vis3[i+p]=0;
v.pop_back();
}
}
}
};
f(f,1);
cout<<ans<<endl;
}
洛谷 P1025 [NOIP 2001 提高组] 数的划分
将整数 n 分成 k 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5;
1,5,1;
5,1,1.
问有多少种不同的分法。
void solve(){
int n,k;cin>>n>>k;
int ans=0;
//vector<int> v;
auto f=[&](auto self ,int x,int sum ,int st)->void {
if(x==k+1){
if(sum==n){
ans++;
}
}else{
rep(i,st,n-sum){
self(self,x+1,sum+i,i);
}
}
};
f(f,1,0,1);
cout<<ans<<endl;
}
洛谷 P1019 [NOIP 2000 提高组] 单词接龙
思路参考自 RyanLi 的个人中心 - 洛谷 | 计算机科学教育新生态
这题难点主要在于字符串的处理...
以下对代码进行了一些注释
void solve(){
int n;cin>>n;
vector<string> s(n+1);
rep(i,1,n)cin>>s[i];
char c ;cin>>c;
vector<int> vis(n+1);
int ans=0;
auto f=[&](auto self, string t)->void{
ans=max(ans,(int)t.size());
rep(i,1,n){
if(vis[i]>=2)continue;
for(int j=1 ; j<min(t.size(),s[i].size()) ; j++){
// 由于 j < t.size() 也就是 j<= t.size()-1,
// t.size()-j >= 1 , 最多从1也就是第二个位置开始取(t取尾,s取头)
// 不会出现例如 at 和 atide 相连, s也不会全部是别人的尾巴
if(t.substr(t.size()-j)==s[i].substr(0,j)){
vis[i]++;
self(self, t+s[i].substr(j));
vis[i]--;
}
}
}
};
// 不能直接f(f,c);递归 因为开头有包含关系而f避免了包含
rep(i,1,n){
if(s[i][0]==c){
vis[i]++; // 这里也要用vis数组进行标记!!!!!!!!!!!!
f(f,s[i]);
vis[i]--; // 这里也要用vis数组进行标记!!!!!!!!!!!!
}
}
cout<<ans<<endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号