图论学习笔记
图的概念
简史
欧拉与戈尼斯堡七桥问题

等价问题:“欧拉一笔画”\(\equiv\)与任一个顶点相关联的边必须是偶数条。
图的基本概念
图
无向图

邻接与关联
邻接与关联:
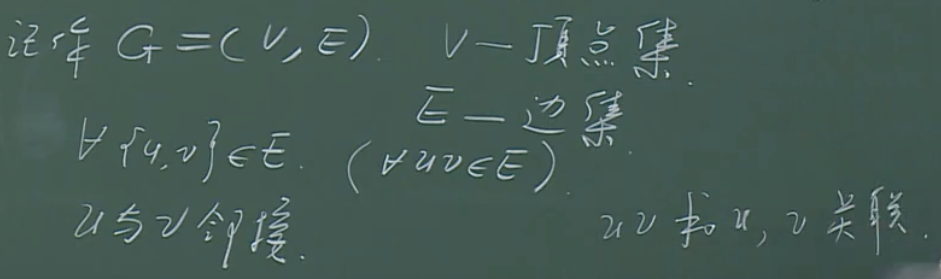
\((p,q)\)图
另一种表示方法:(p,q)图
图相等与特殊的图
图相等、特殊的图(平凡图、零图)
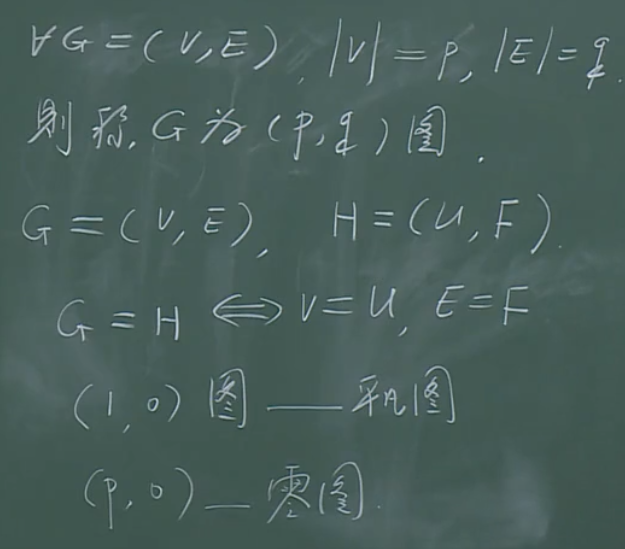
有向图

疑惑:无向图是集合反自反、对称的关系。有向图中为保证反自反性,去掉了自身到自身的有向线段\(\{(v,v)|v \in V\}\)。但是,图是不允许存在自身到自身的边吗?
答案:是的。

图的表示
图解法与邻接矩阵法
图解法与邻接矩阵法:
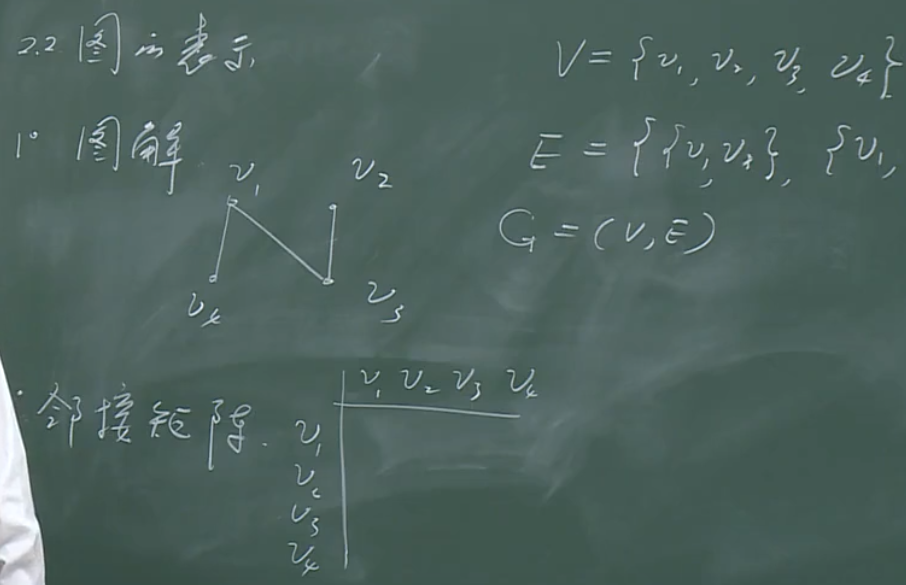
问题:关系的闭包在图中的意义是什么?
图模型
利用图建模现实问题,并用图的理论加以解决的能力。
例子:结婚问题、地图与导航
子图
子图概念
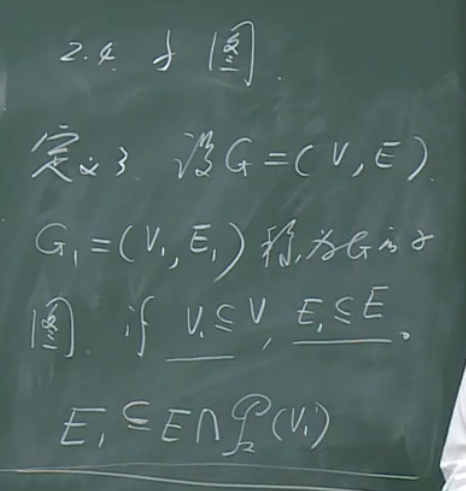
生成子图
特例:生成子图

记号:去除顶点u,去除边{u,v}
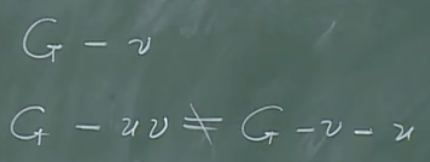
尤其地,注意去除边的记号不是去除u、v两个顶点。
导出子图
(1)顶点导出子图:若V1⊆V(G),则以V1为顶点集,以两个顶点均在V1中的边集组成的图,称为图G的顶点导出子图,记为G(V1)。
例如:求G(V1),V1 ={1,3,5}
则G(V1)为

(2)边的导出子图:若E1⊆E(G),则以E1为边集,以E1中所有边的顶点为顶点集组成的图,称为图G的边的导出子图,记为G(E1)。
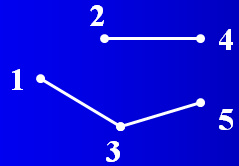
例如:求G(E1),E1 = {13,24,35}
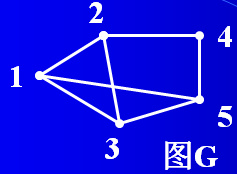
则G(E1)为
度
度的概念

定理1——握手定理
【定理1】握手定理
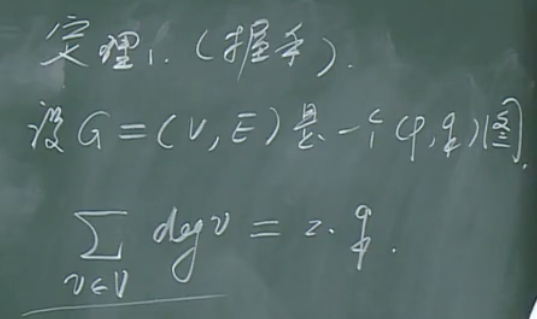
证明:每一条边对度数总和的贡献为2(每一条边对应两个顶点),由于共有q个边,故度数总和为2q。
推论1:握过奇数次数手的人为偶数个。
证明:将人分为两类,握奇数次手\(V_1\)和握偶数次手\(V_2\),
那么,\(V_1\)与\(V_2\)中顶点的度数总和为偶数(2q),
同时,\(V_2\)的度数之和必然为偶数,
那么,\(V_1\)的度数之和必然为偶数(偶数-偶数=偶数),
同时,由于\(V_1\)中均是握奇数次手(\(V_1\)中各顶点度均为奇数),
那么,\(V_1\)中顶点数必为偶数个(偶数个奇数之和=偶数)。
最小度数与最大度数
图G的最小度数和最大度数:
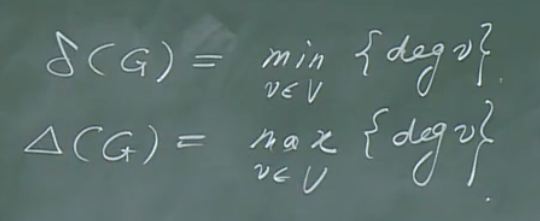
正则图
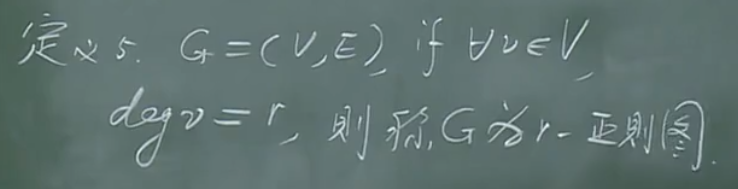
2-正则图

3-正则图

完全图
完全图\(K_p\):(p-1)正则图
完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
双图中的完全图:\(K_{m,n}\)

图建模:

用反证法证明:
假设任意两个顶点,其度数均不相同。那么,n个顶点必然有n种度数,即:
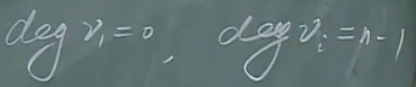
\(degv_i=0\)代表没有顶点与之邻接,而\(degv_j=n-1\)代表与其他所有顶点邻接。
这显然是矛盾的,因此,原结论得证。
注意:证明过程中是使用的度的定义,而不是抽屉原理。
同构
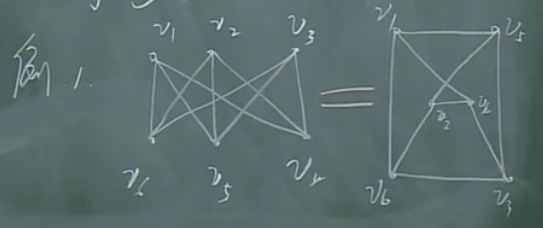
图里是双图中的3-正则图,是完全一样的两个图。
同构的概念

两个图结构一样,但是顶点名字不一样了。(顶点集合上的置换)
那么,什么条件下可以称两个图是同构呢?
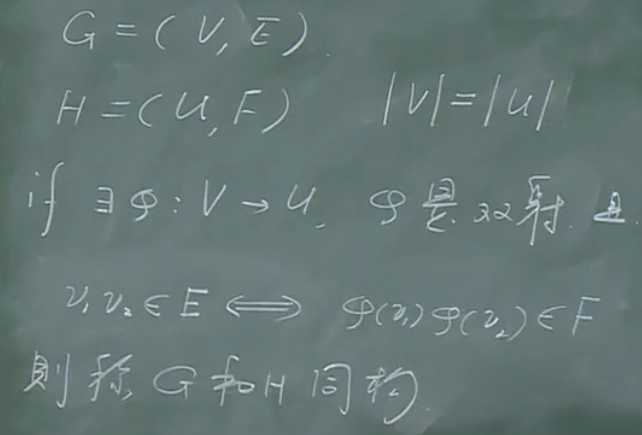
注意:双射是指既是单射又是满射的映射称为双射,亦称“一一映射”。
同构的应用
例如,判断基因是否相似。
乌拉姆猜想

注意:乌拉姆猜想并未被证明。
路、圈、连通
连通是图论里最重要的概念。
通道
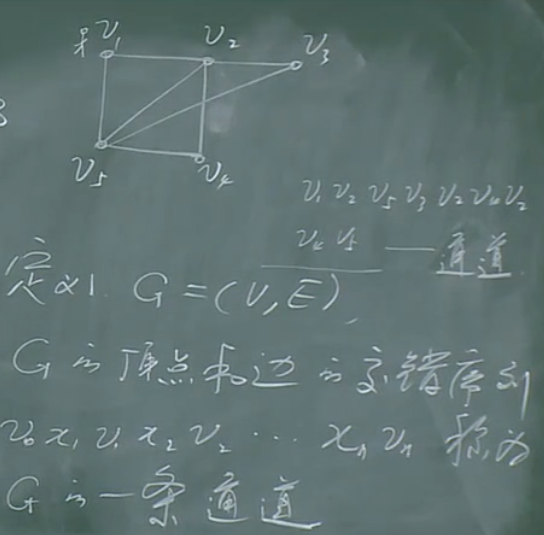
通道的长为边的个数。
闭通道:\(v_0=v_n\)时,称\(v_0v_n\)通道为闭通道。
迹
迹与闭迹的概念:
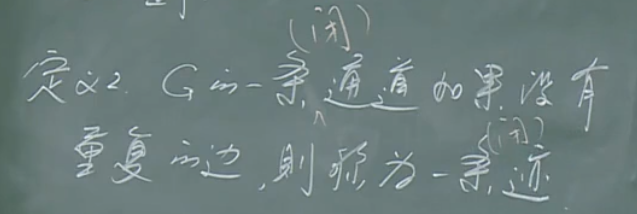
路和圈
路、闭路(圈)的概念:

与集合论的联系:
u、v之间有直通的路\(\Leftrightarrow\)u、v关系矩阵相关元素为1
u、v之间有不知长度的路\(\Leftrightarrow\)u、v传递闭包矩阵相关元素为1
判断一个图有没有圈:
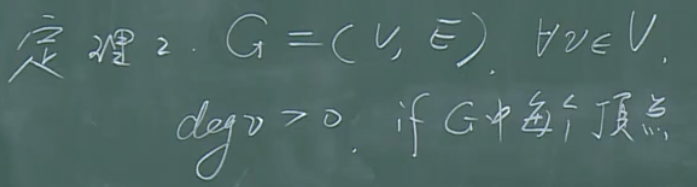

证明方法:
最长路法,图论中常用的证明方法(因为图是有穷系统上的二元关系,因此必然存在最长路)。

推论:

有意思的题目:安排大量朋友吃饭,其中每个人的朋友数(互相)大于等于m,那么,每桌安排m+1个人最合适。
因为这种安排可使每位吃饭的人左右均是朋友。
放宽条件的定理:

路和圈的另一个定理:
【定理】假设\(G=(V,E)\),\(u,v\in V\),如果u、v之间有两条路,那么图G中有圈。
【证明】
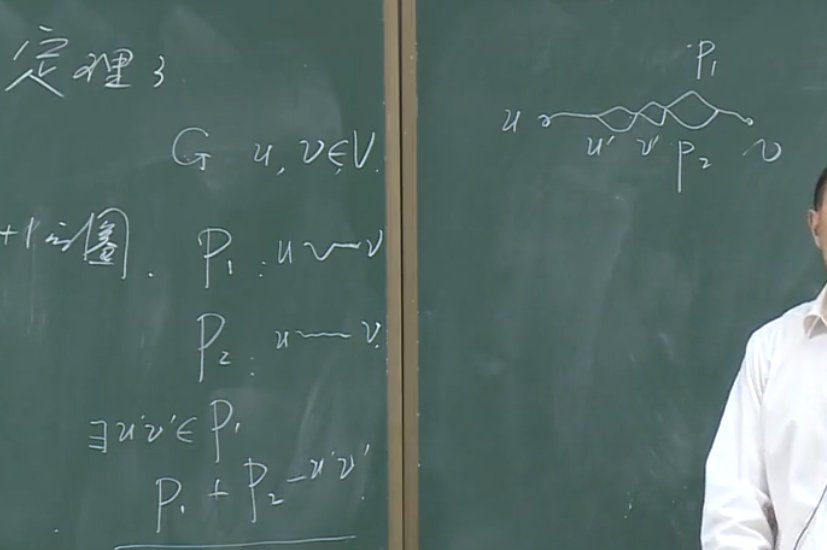
注意:
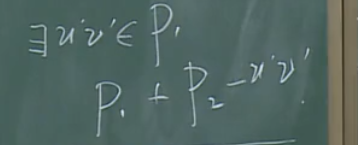
为什么\(p_1+p_2-u'v'\)连通就代表\(p_1\)、\(p_2\)是不同的路呢?
连通
连通的定义:
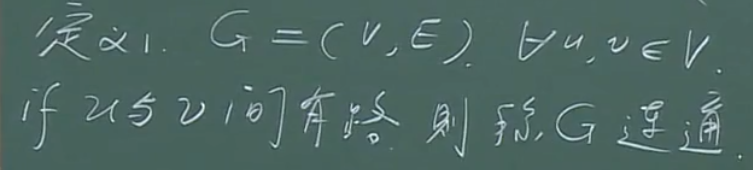
判定方法:
-
充分条件
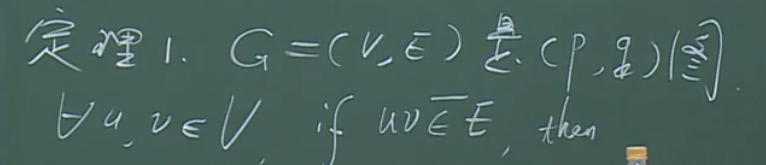
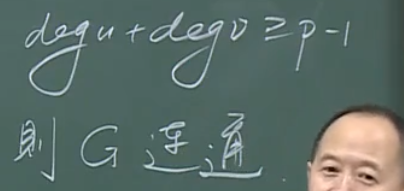
充分条件是一个很强的结论,也就意味着其条件近乎苛刻。我们更希望得到充要条件。
充要条件是很好的结论,其“要”字表明,不满足其条件的话,则一定不成立。证明方法:
推导过程:

直观的说,这个不连通的图可以说为是分块的(划分/等价)。那么,依据什么关系进行划分呢?
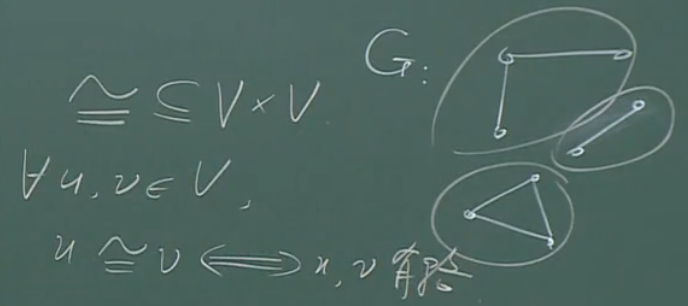
验证上述关系是不是自反、对称、传递的。
自反:自己和自己之间有路;
对称:u和v之间有路,则v和u之间有路;
传递:u和v之间有路,v和w之间有路,则u和w之间有路。对谁进行划分呢?
那么,很自然的这个等价关系就是对顶点的划分。
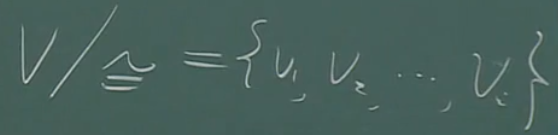
\(V/\cong\)表示的是集合V关于\(\cong\)的商集合,也称之为等价类。商集是集合论的基本概念之一,指由集合和该集合上的等价关系导出的集合。设~是非空集合A的一个等价关系,若把以A关于~的全部等价类作为元素组成一个新的集合B,则把集合B叫做A关于~的商集合,简称为商集,记作B=A/~。
例子:
A={a,b,c,d,e,f}={某大学宿舍的大学生};R是A上的同乡关系(不难证明同乡关系是等价关系),若a,b是北京人,c是广东人,d,e,f南京人,则R={(a,a)(a,b)(b,a)(b,b)(c,c)(d,d)(d,e)(d,f)(e,d)(e,e)(e,f)(f,d)(f,e)(f,f)}.A中各元素关于R的等价类分别是:
[a]R=[b]R={a,b};
[c]R={c};
[d]R=[e]R=[f]R={d,e,f};
A关于R的商集A/R={[a]R,[c]R,[d]R}={{a,b},{c},{d,e,f}}.对这个划分的准确定义是什么呢?
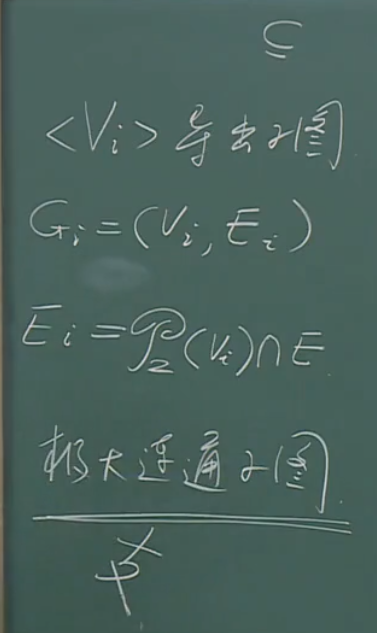
很明显,连通子图(顶点各等价类的导出子图)不仅包括顶点,还包括相应的边。
子集属于偏序关系(给定集合的子集的集合(它的幂集)按包含排序),因此采用“极大”而不是“最大”一词(极大表示找不出一个子集具备此性质(连通),且真包含这个集合)。
这个极大连通子图称之为图的一个支。图论常用证明方法:
-
演绎推理法。
-
反证法。
-
数学归纳法。
常用数学归纳法。当某一个问题与自然数相关时,数学归纳法比较好用。
由于图论是一个有穷系统上定义的唯一的二元关系,有穷系统一定与自然数关联。
但是,归纳法是一种无趣的方法。
此处使用反证法。
证明过程:
-
法1


有了支的概念,证明变得简单。
-
法2
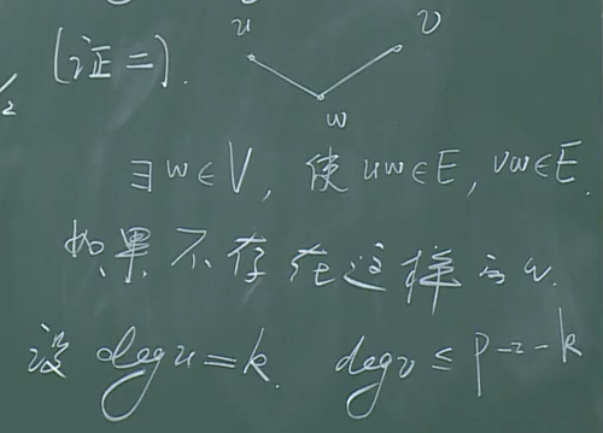
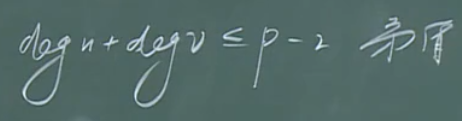
此处,\(\mbox{deg}\ v\le p-2-k\)的原因是:由于v与u之间不连通,以及v与自身不连通(?),故-2;另外,与u连通的节点均不能与v连通,故再-k。
副产品:如果\(\mbox{deg}\ u+\mbox{deg}\ v\ge p-1\),则u、v之间必然有一条长为2的路(很短)。
推论:
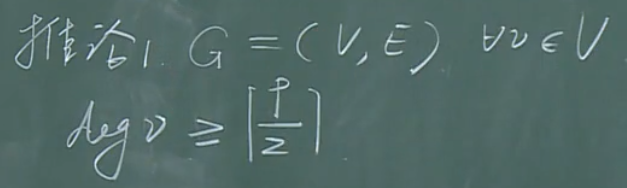
-
补图、双图(二部图)
补图
补图的定义:

注:同构的图的补图也是同构的。
注意:图和自己的补图有可能是同构的,称之为自同构,或自补。
引入补图的意义:
为了方便。在图中讨论不方便的问题,可以考虑在其补图中考虑。

在图论中,这个问题即为:
在六个顶点的无向图或者其补图中,一定存在三角形。
注:在五个顶点的无向图及其补图中得不到这样的结论。
Ramsey理论:
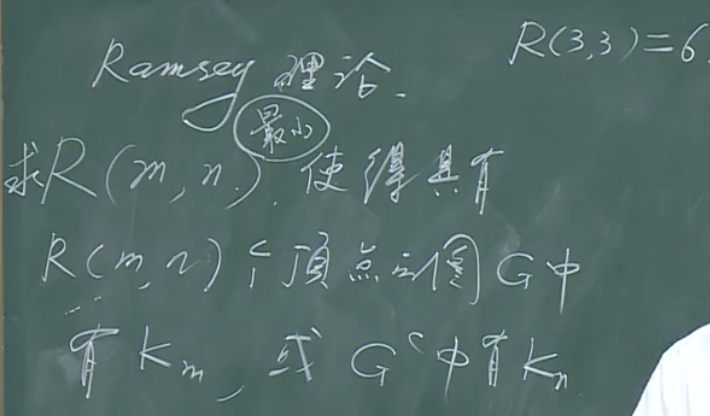
双图
双图的定义:

双图内的圈都是偶数(包括0)吗?
这个特征是本质特征吗?(是否充要)
是充要条件。

【证明1】
-
必要性。

必要性的证明是显然的,在写完之后,立马可得n是偶数。
因为相邻的顶点分别属于不同的划分,于是下标n与下标2同为偶数。 -
充分性。
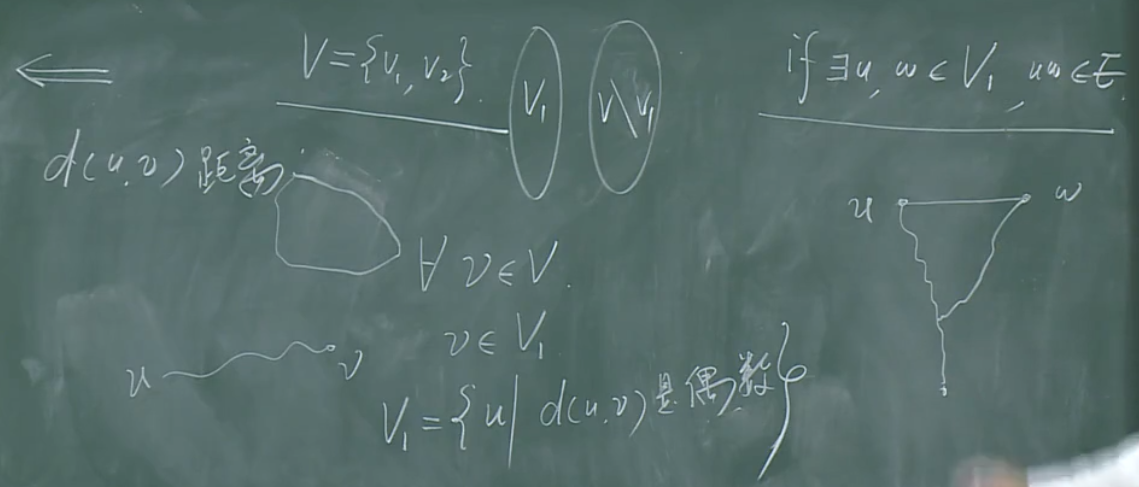
构造的方法生成\(V_1,V_2\)两个划分。
-
\(\mbox{if}\ u,w\in V_1,uv\in E\)
立马可得矛盾。因为\(V_1=\{u|d(u,v)是偶数,\forall v\in V_1\}\)。
-
\(\mbox{if}\ u,w\in V_2,uv\in E\)
亦存在矛盾。
因为\(V_2=\{u|d(u,v)是奇数,\forall v\in V_1\}\),那么
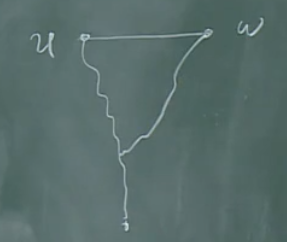
两条边的长度之和为偶数,加上u,w之间的长度为奇数(1)。
-
【证明2】
用染色法。从某个点开始逐层交叉染色,在染色过程中:
若发现有某条边的两个端点着色相同,则必定存在奇数环①,与题意相矛盾。
若没有发现,则根据染色法原理,每一条边的两端着色必然不同,那么根据二分图的定义,就可知这个图是一个二分图。
①的证明:
不妨设这条边的两个端点着色都为1,且这两点必然是由同一个源点扩展而来。那么根据染色法原理,因为这两个点的着色相同,那么从源点到这两个点所经过的边数(假设分别为x和y)的奇偶性必然相同,那么这个环的总边数为x+y+1,由数学知识得这个数必然是奇数。
证毕!
【推论】
也就是说双图中一定不存在三角形。
没有三角形并不一定是双图(也即反之不真)
【例】

问两图是否同构?
【解】显然,两图并不同构。
原因在于,上图很明显是双图,而下图中有三角形(圈长度为3)。
完全双图:
完全双图\(K_{m,n}\)是具有\(m\cdot n\)条边的双图,其中\(|V_1|=m,|V_2|=n\)。
没有三角形的图中,完全双图边最多。
图兰定理
定理
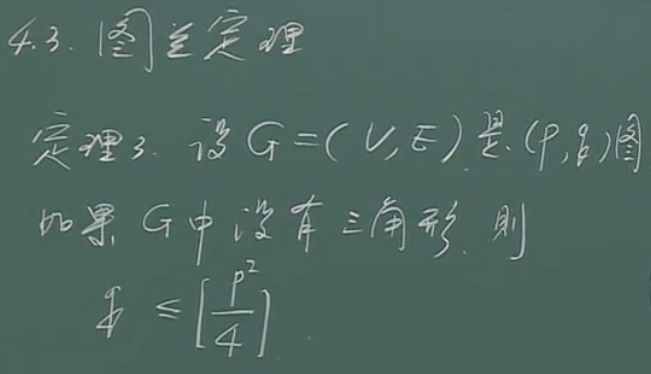
证明
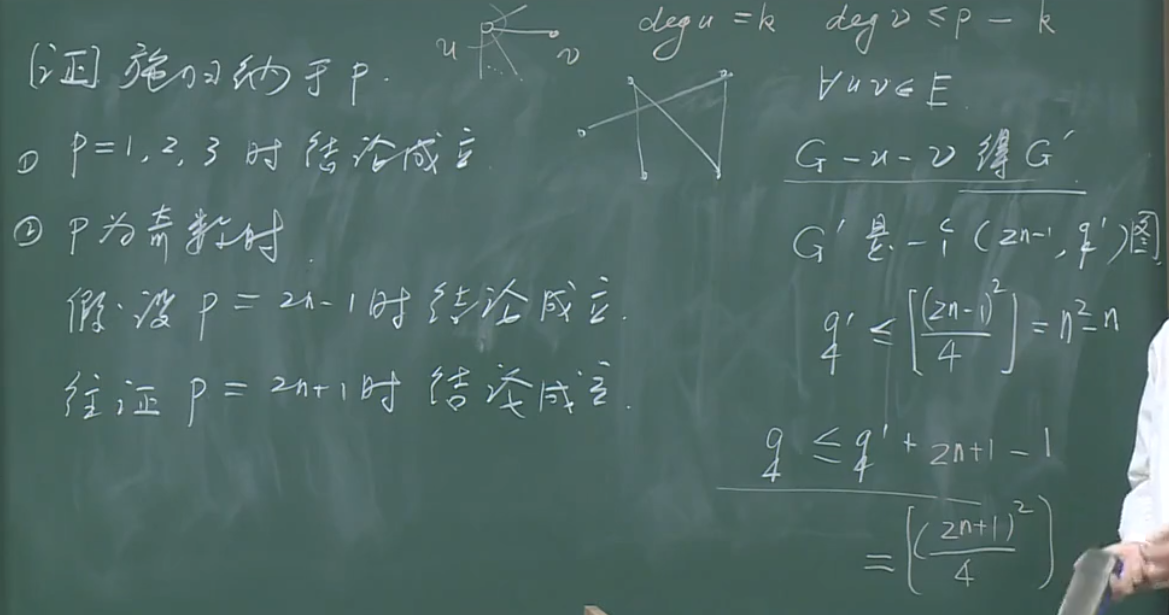
注意:利用数学归纳法证明时,从p=2n-1到p=2n+1的证明过程中所写的\(q\le q'+2n+1-1\),加上的\(2n+1=k+2n+1-k\)(从2n+1个顶点中去掉顶点u和v之后所减少的边的和),最后减一是因为u、v之间的边被重复的计算了。
极图理论
引子
工兵排雷问题
欧拉图
欧拉迹、欧拉闭迹
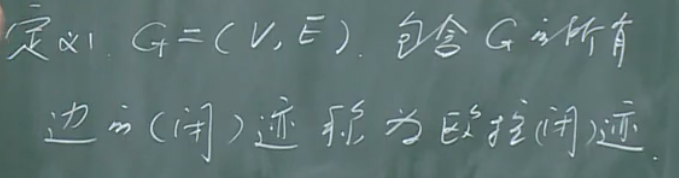
欧拉图定义

迹:没有重复边的通道。
欧拉迹:没有重复边且边全部包含的迹。(戈尼斯堡七桥问题)
欧拉图的判定(欧拉定理)
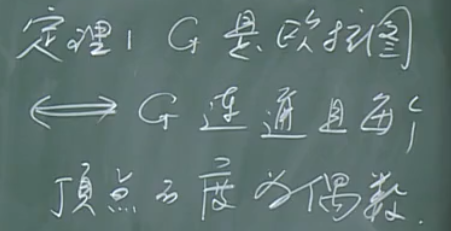
欧拉定理在伪图上的结论
伪图

多重图和带环图(违反了反自反性)统称为伪图。
欧拉定理在伪图上依然成立
一笔画问题
相比于欧拉图(一笔画成且回到原点),不再要求回到原点,一笔画成即可。
【定理2】

【证明】
在两个奇数度顶点上加一条边,使之成为伪图(多重图)。
由于欧拉定理在伪图上依然成立,因此此图中有欧拉闭迹。
那么,去掉所加的这条边,自然就存在一欧拉开迹(可一笔画)。
【定理3】

也就是说,对于不能一笔画的图,这个定理给出了所需的最少笔数。
哈密顿图
背景
哈密顿在1859年做的“环游世界”装置,正十二面体上的20个顶点,能否找到一个包含所有顶点的圈(生成圈)。
判断一个图是否为哈密顿图的充要条件是一个NP难问题。
定义
【定义1】

闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶点的路径称作哈密顿路径(Hamiltonian path)。
判断方法
判不是
【染色法】对一个图每条边两侧的顶点染不同的颜色,如果这幅图可以完全染色,并且染色后两种颜色的顶点个数不同,则此图一定不是哈密顿图。
解释:为了形成生成圈,其两种颜色的顶点必然前后相接并形成圈,因此其个数必然相等。
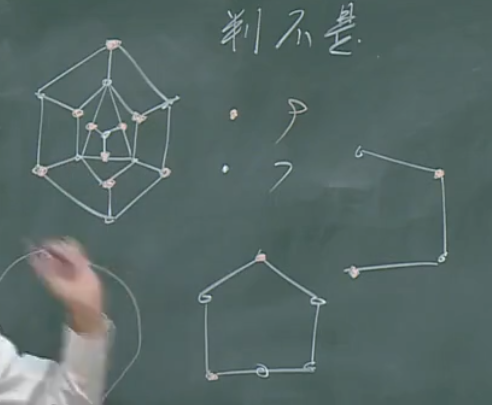
注意:这仅仅是一种判不是的方法,另外需要注意,其条件要求能完全染色。如果
1、对于无法完全染色的,方法失效(不一定不是哈密顿图);(部分可采用加边法解决,要在哈密顿圈上加边)
2、对于染色后顶点个数相同的,此方法无法判断其为哈密顿图;
必要条件
【定理1】

其中,\(G-S\)代表从图G中去掉子图S中所包括的顶点,\(w(G-S)\)表示去掉之后形成的支数。
例如在下图中,如果在右下角去掉两个顶点,仅有一个支,在中间去掉两个顶点,也仅有两个支。

充分条件
【定理1】(Dirac定理)
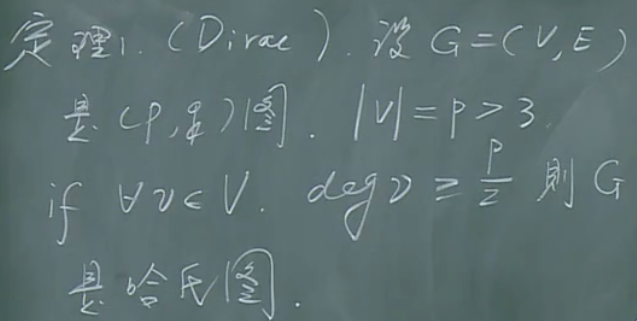
解释:当边多的时候,则存在哈密顿圈。例如,完全图中必然存在哈密顿圈。
【证明】
posa的证明方法:证明其逆否命题,如果一个图G不是哈密顿图,则\(\exists v\in V,\mbox{deg}\ v\le \frac{p}{2}\)。


原因是如果\(v_p\)与\(v_{i_j-1}\)相连(例如图中与\(v_2\)相连),则\(v_1v_3v_4\cdots v_pv_2v_1\)是一个哈密顿圈。
而此时不是一个哈密顿图,不能存在哈密顿圈。

-k的原因如上所述,是因为不能与和\(v_1\)相连的k给顶点的前一个顶点相连(也是k个),-1的原因是不与自己相连。
【定理2】(Ore定理)
这是一个由Dirac定理的上述证明过程导出的定理。
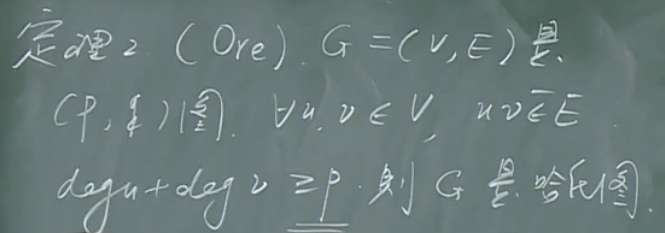
【定理3】(非充分条件)

【证明】
反证法。(仍受posa证法的启发)

注意:
1、当最长路的长度\(k<p\)时,那么最常路必然形成圈,而又由于\(k<p\),在圈外必然仍有与之连通的节点,那么,这就形成了更长的路,则与假设矛盾。
2、必然形成圈的原因在于,【定理1】的证明中所用到的关于度的证明,如果要求两点度数之和大于等于p-1,那么\(v_p\)必须与\(v_{i_j-1}\)相连,而这个相连就会导致圈的形成。
图的表示
邻接矩阵

- 邻接矩阵的阶是顶点个数。
- 对角线上全是0。
- 矩阵的是对称的。
- 每一行上1的个数是该顶点的度。
- 1的个数除以2等于边的条数。
- 同构图的邻接矩阵相似。
由上图中的\(v_3\)经过6步到达\(v_1\),问有多少种走法?
【定理1】

也就是说,走法是\((B^l)_{ij}\)种。
【证明】
证明方法使用数学归纳法,使用到的是线性代数知识。
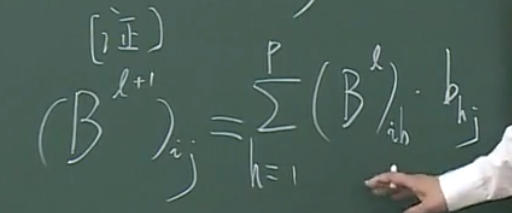
但是,值得注意的是在图论中,其意义如何。
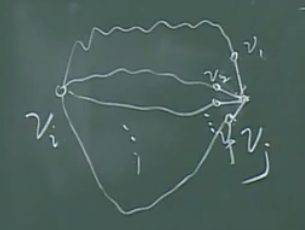
也就是说,把最后一步摘出来,这是其在图论中的意义。
邻接表

关联矩阵

图中\(e_1、e_2\)等表示相应的边,也就是说这个矩阵反映了顶点与边的关系。
应用:如表示电路节点间关系。
特点:
- 每一列都是两个1;
- 每一行是顶点的度。
图解
优点:直观,容易产生灵感。
带权图

定义
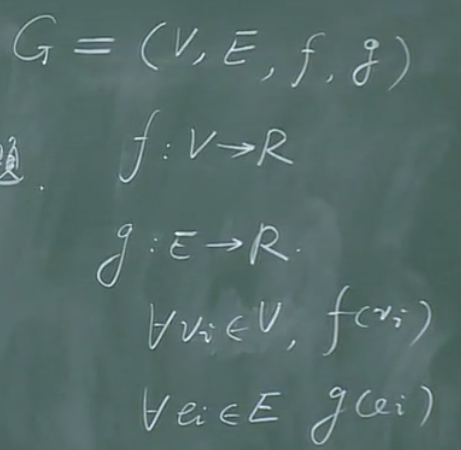
应用
异构信息网:
顶点不是一类,边可以在同类或不同类间连接。
例如:论文数据库
典型问题
最短路径问题

分类:
-
单源最短路径
不含负权重,Dijkstra算法。
-
任意两点均求最短路径
求传递闭包,Floyd算法,\(O(p^3)\)。
中国邮路问题
必须走遍所有的路。
除去权重,可视为欧拉迹。
在没有欧拉回路的情况下,所有奇度顶点之间的路需要走两遍,这就涉及到优化问题。
旅行商(货郎担)问题
必须走遍所有的顶点。
除去权重,可是为哈密顿回路。
树与割集
树
定义
森林:
没有圈的图称之为森林。
连通的森林即为树。
特殊的树:
平凡树:只有一个顶点的树。

叶子:树中度为1的节点。
推论1:

其证明方法是树也是一种图,则其有一条最长路,最长路两个端点的度均为叶子。
推论2:
数是双图。
【证明1】
一个图是双图的充分必要条件是圈为偶数个。
而树的圈为0个,符合条件。
【证明2】
可使用染色法证明。
注意:这是论证,而不是给一个具体的图通过染色结果来判断。
性质

如果互相(两两)证明为充分必要条件,则证明过于繁琐。
我们采用如下证明方法:
1到2:
这是由于,如果两个顶点间具有不同的路,则一定有圈,与树的定义相悖。可以用反证法具体论证。
2到3:
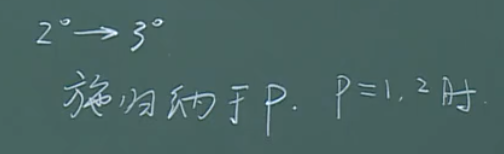
注意:这里要使用第二数学归纳法。

3到4:
连通自然是得不到无圈这样的结论的,因此必须利用好\(p=q+1\)这一条件。
圈与p、q之间的关系在于,对于圈\(p=q\)。那么,用反证法证明。

假设存在圈\(C_n\),其中有n个顶点,则\(n\ge 3\),且\(n<p\)(原因在于圈中顶点数与边数相等,故\(n\le q<p\)。
又由于此图连通,故圈与圈外顶点(p-n个)有边,边共有p条,矛盾。
(4到5):
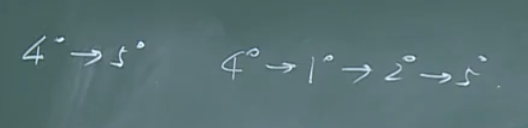
由于4到5不好证明,而2到5好证明,因此使用这种方法证明。
4到1:

假设不连通之后,就应该想到图中有至少两个支,而这些支内部是连通的。
而图是无圈的,则其支中自然无圈。
那么,每个支就是树,满足\(p_k=q_k+1\)。
相加可得\(p=q+k=q+1\),得出支为1个,矛盾。
5到1:
只需证该图连通即可。
可采用反证法,假设其不连通,则至少存在两个支。从两个支中取出两个顶点,自然是不邻接的,在两个顶点间加上一条边,图中也不会形成圈。
因此,与任意两个顶点间加一条边可形成一个圈矛盾。
极小连通图
【定义】
【解释】
连通的最弱情况,去掉一条边则不连通。
【定理】
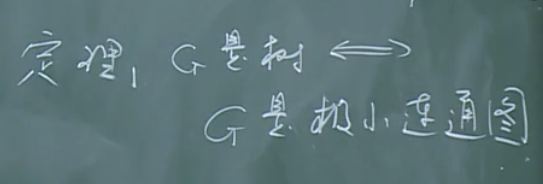
极小连通是树的等价定义。
树的中心
顶点偏心率
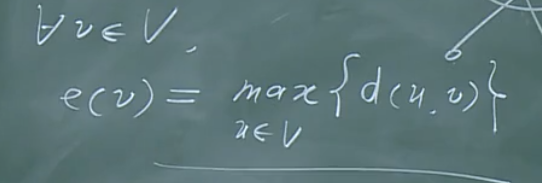
树的半径
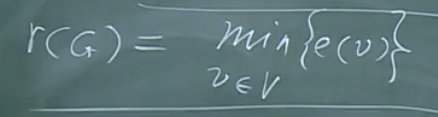
树的中心
【定义】
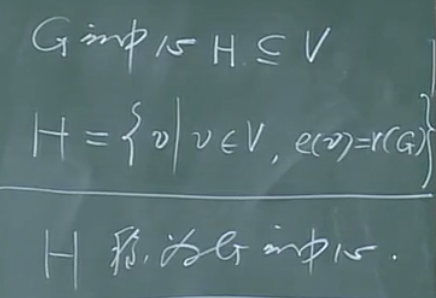
【求法】
可以像剥白菜一样求之,每次去掉其最外围的叶子节点,其中心不变,其半径减一。
【定理】
树的中心是一个或者是两个。
【证明】
两种思路:
1、不停的去叶子节点,直到最后为2个或1个才能停止。
2、从其最长路出发,最长路的节点数一定是奇数个或偶数个。
生成树
定义
【引入】
村庄自来水问题:
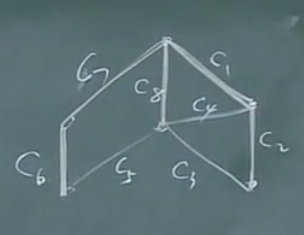
【定义】

存在性定理
是不是每个图都有生成树呢?
并不是这样的。
【定理】

【证明】

“破圈法”是指:在图G中如果存在圈,则去掉其一条边,使之保持连通且去掉这条边。如此重复,由于图是有穷的,必然可以得到其生成树。
生成树的个数
生成树的个数上界:
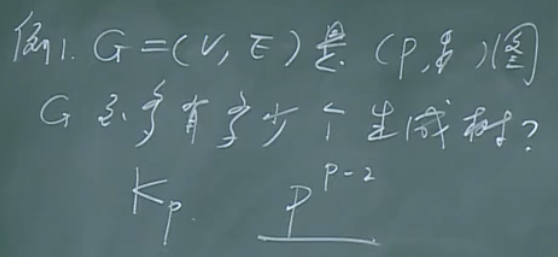
这个只是可能的上界,具体怎么求有多少个呢?
生成树的个数求法:

假设B是邻接矩阵,D是顶点度数矩阵,
其Kirchhoff矩阵\(K=BB^T=D-B\),
其n-1阶主子式的绝对值是生成树的个数。
(具体会在组合数学中探讨)
最小生成树
定义
加权图:
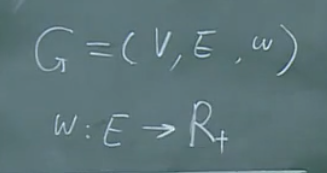
最小生成树:
【定义】

算法
Kruskal算法:
先对边按照权值排序,然后从最小的权值边开始,逐步组成生成树。
但是在这一过程中,要注意判断不要生成圈。
Prime算法:
从任一顶点出发,然后选择与已选顶点集相连且权值最小的顶点,逐步组成生成树。
但是在这一过程中,要注意判断不要生成圈。
两种算法的简单对比:
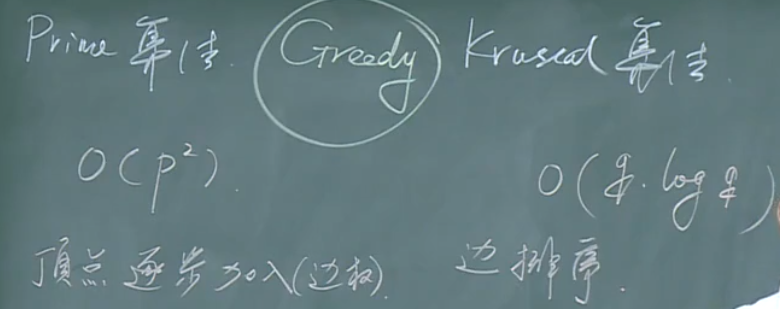
这两种算法将在数据结构中详细论述。
这两种算法,体现了Greedy策略(贪心策略)。
割点与桥
割点
割点的定义
【引入】

离散数学数学修养的要求:
1、了解背景;
2、会用图解;
3、会用数学(集合论)语言描述。
【定义】
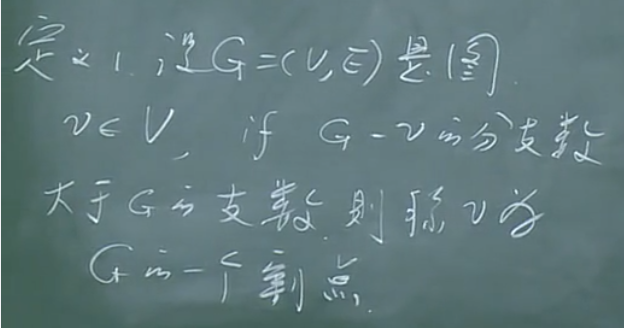
【推论】
-
哈密顿图中不存在割点。/有割点的不是哈密顿图。
哈密顿图中存在哈密顿圈,此圈中包含所有顶点,去掉里面的任一个顶点不能增大其分支数。
-
每个非平凡图中至少有两个点不是割点。
非平凡图中,考虑其最长路,最长路的两端点不可能是割点。
割点的性质
割点的特征性质(与定义等价)

此处注意:如果G不连通,此结论也是成立的,但是证明过程会更繁琐。

很明显,3得证之后,2自然可得,故选择\(1°\Rightarrow 3°\Rightarrow 2°\Rightarrow 1°\)。
证明过程并不复杂,不再赘述。
桥
桥的定义

桥的性质
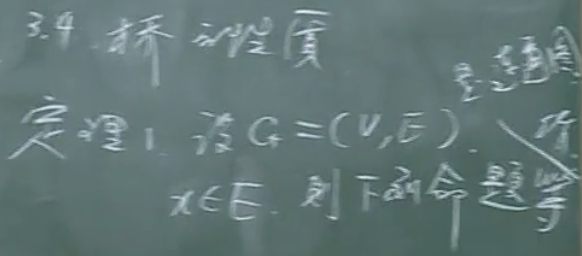

小结
许多好算法与树有关,许多模型首先得到的是图。(例如:传感器网络)
这就是树的重要性。
要知道什么样的树可以更好地表达图的性质。
有向树更有实用性。(最后一章)
【例】???
证明R的等价闭包(\(e(R)\))与传递闭包有如下关系:
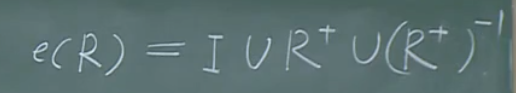
【证明】
等价闭包可以认为是自反对称传递闭包。
使用集合相等的常用证明方法:
-
左边\(\subseteq\)右边
\(e(R)\)是包含R的等价关系中最小的那个集合,因此,只需要证明右边是包含R的等价关系即可。
这几乎是显然的。因为,\(I\)是自反的,\(R^+\cup (R^+)^{-1}\)是对称且传递的。 -
右边\(\subseteq\)左边
任意找出一个S,要求\(S\supseteq R\)且S是等价的。
由于\(e(R)\)是所有S的交集,且S是任意的,
那么,要证明右边\(\subseteq e(R)\),证明右边\(\subseteq S\)即可。
可以任意假设一个序对\(<x,y>\in I\cup R^+\cup (R^+)^{-1}\),
然后分为:-
\(<x,y>\in I\)
显然,\(<x,y>\in S\)。因为S是对称的。
-
\(<x,y>\in R^+\)
显然,\(<x,y>\in S\)。
-
\(<x,y>\in (R^+)^{-1}\)
可通过若S是对称的,则\(S=S^{-1}\)来考虑证明。
-
连通度与匹配
连通度
引入
直观了解
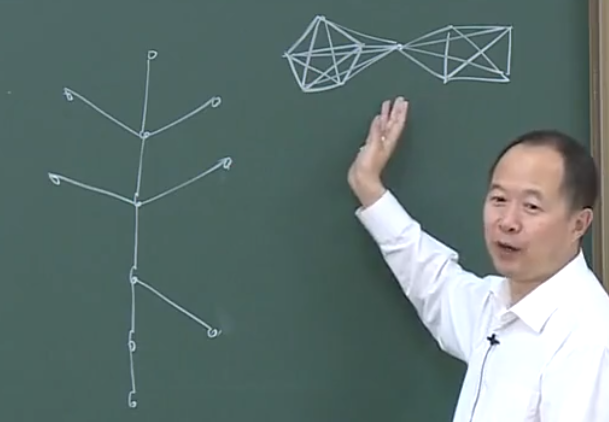
通过对这两个图连通能力的比较,可以知道在顶点上考虑,两幅图连通能力相同。(去掉1个顶点即不连通)
但在边上考虑,明显右图的连通能力更强些。(左图去掉1条边,有图去掉4条边才能不连通)
因此,连通度需要在边和顶点两个层面上考虑。

但是,对于图\(K_5\),去掉几个顶点/边才能使之不连通呢?
可见上面的说法对于这样的图并不方便。需要更方便使用的定义。
研究背景
铁路网、公路网与计算机互联网如果建设成第一幅图中的样子,会过于脆弱。
但若建设成第二幅图中的样子,又并不现实。
但是,以互联网为例,主节点之间希望可以建成如第二幅图中的样子,增强容错性。
我们需要对这种连通能力进行度量。
定义
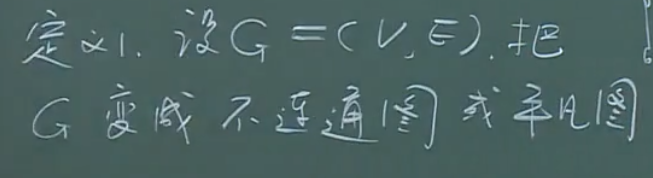
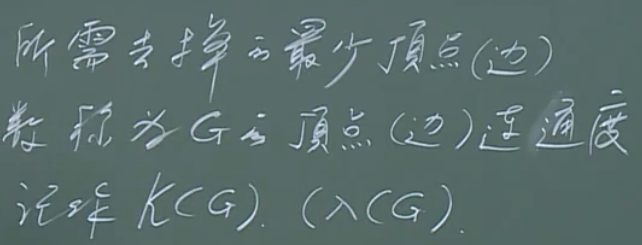
注意:
定义中没有提到图G是不是连通的,也就是说不连通的图G也有其连通度。
【例1】


其中,T表示树。
【例2】
除了连通度,最小度\(\delta (G)\)也可以反映一副图的连通程度,但没有连通度描述的精确。
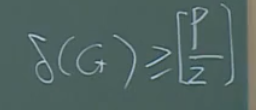
注意:这这是连通的充分条件,并不能将这个条件视为连通(不能当成充要条件)。
\(\kappa (G)\)、\(\lambda (G)\)和\(\delta (G)\)的关系
【定理1】
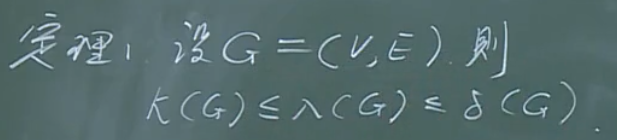
【证明】
在这个结论当中,\(\lambda (G)\le \delta (G)\)最容易证明。
(原因是在不等式关系中,越不精确的越容易证明。)
因此,先证\(\lambda (G)\le \delta (G)\)。
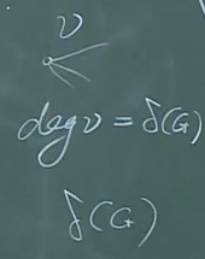
根据顶点最小度的定义,也就是说对于这样一个顶点v,只需要去掉与之关联的\(\delta (G)\)条边,则其一定不连通。
也就是说\(\lambda (G)\le \delta (G)\)。
这部分严格的证明过程如下:
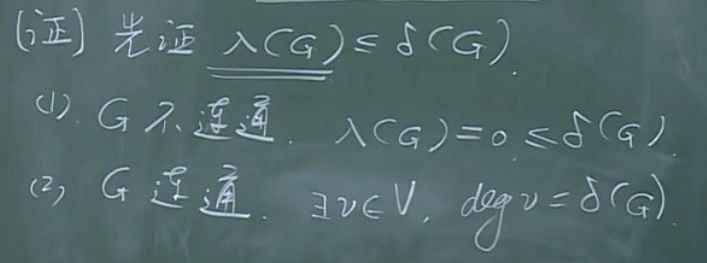
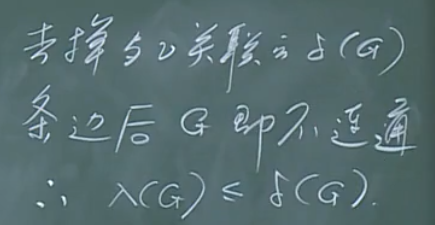
然后,证明\(\kappa (G)\le \lambda (G)\)。
在这里要注意平凡图是连通的。
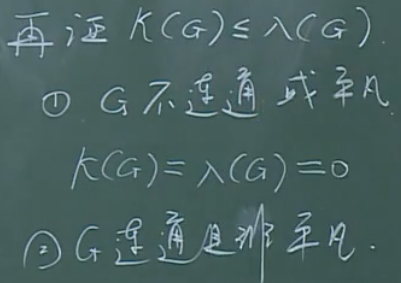
明显地,若假设去掉\(\lambda (G)\)条边之后图不连通,那么去掉与之相关联的顶点也是可使图不连通的。
进一步地,再分两种情况讨论。??这里如何证明的\(\kappa (G)<\lambda (G)\)
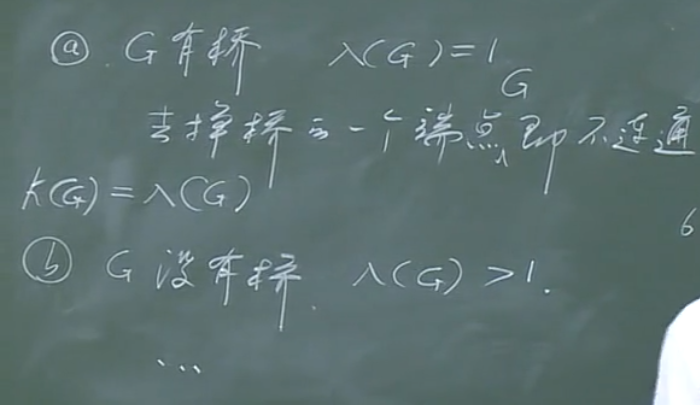
【定理2】

【证明】
证明存在性定理往往使用构造法。
但应该注意,构造法往往只能用于证明其存在,如果直接使用构造出的图,可能实际应用效果很差。
-
\(a=b=c\):
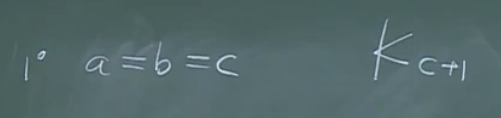
-
\(a=b<c\):
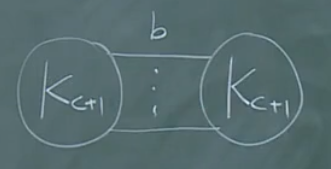
-
\(a<b=c\):
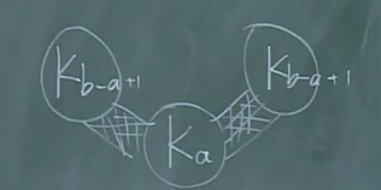
网格线代表中心子图中每个顶点均与外面顶点相连。
需要去掉的边:
使\(K_{b-a+1}\)不连接的b-a个,加上与中间相连的a个。 -
\(a<b<c\):
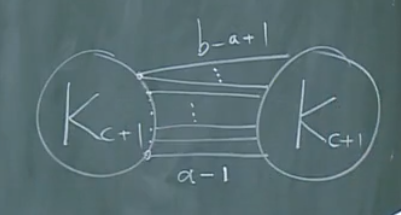
能否根据【定理2】改进【定理1】的结论呢?
答案是不能改进。
但是,如果增加一些条件(使G中的边多到一定程度),可以得到新的结论(\(\lambda (G)=\delta (G)\))。
【定理3】
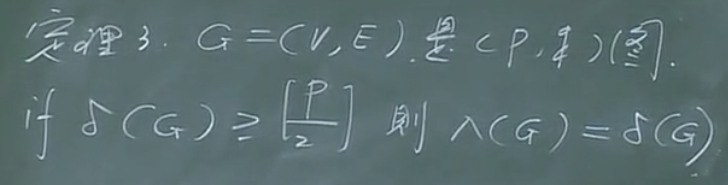
【证明】
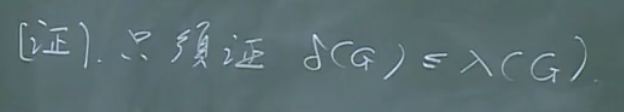
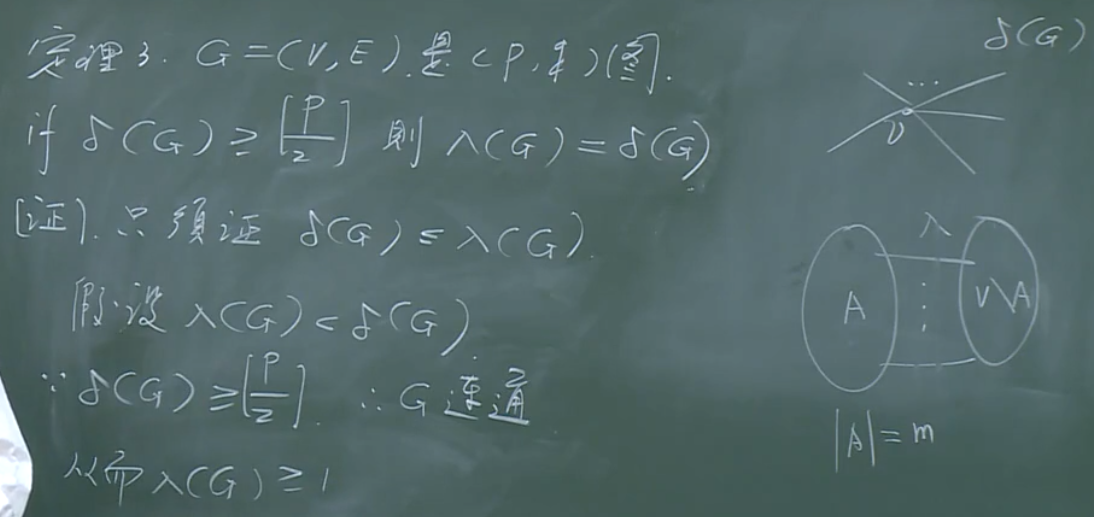
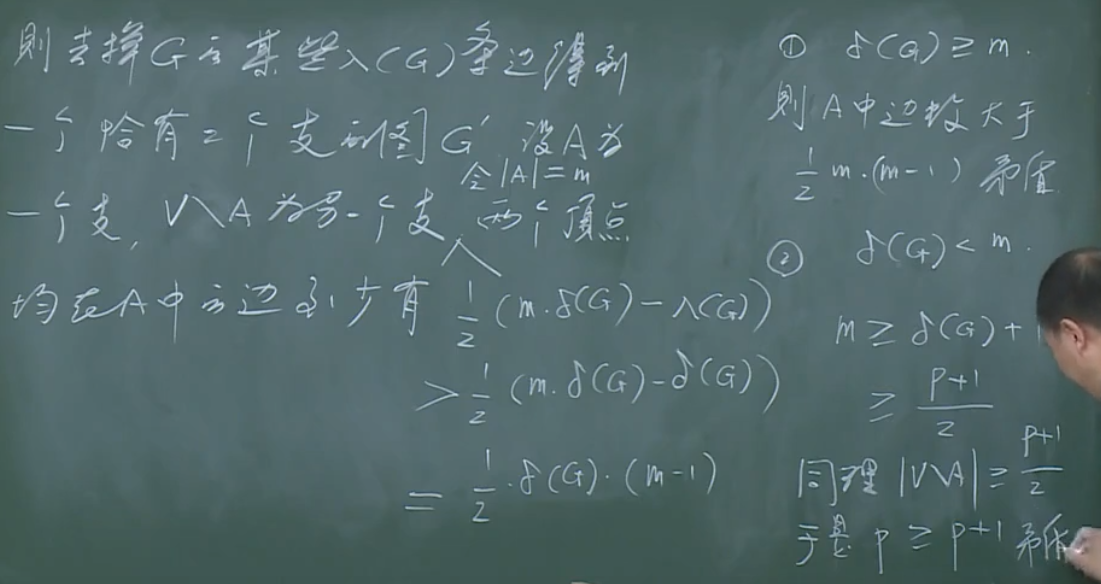
n连通
我们希望描述对一大类图的性质,因此,我们定义图集\(\mathcal{G}\)。
【定义】

n连通不仅仅是针对特定的某一个图的概念,例如,树都是1连通的。
再如,我们说这个图是2连通的,那么也就是说这幅图去掉一个顶点仍是连通的。
怎么描述这样的一幅图呢?
【定理1】

【证明】
\(\Leftarrow\)是显然的。
由于其任意两个顶点在一个圈上,也就是说这两个点不是割点,由于取点的任意性,得出图G上没有割点。
那么,\(\kappa (G)\ge 2\),也即图G是2连通的。
\(\Rightarrow\):
分析可知,找不到明确的思路正向证明,反证法也没有好的思路。
只能尝试使用数学归纳法。
由题意,如果使用归纳法,重要的找到对什么施归纳。
由于要证明的u、v之间有路,为了方便描述,我们取最短路(距离\(d(u,v)\))。
那么,只需假设\(d(u,v)<k\)时成立,证明\(d(u,v)=k\)时成立即可。
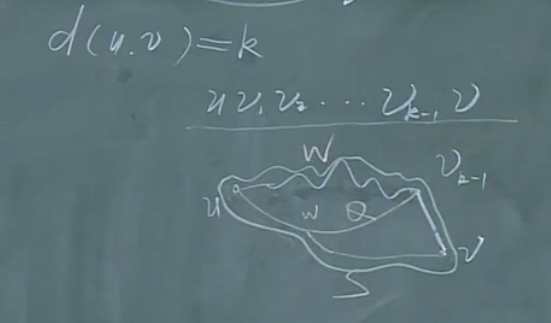
大概的思路在上图已给出。
-
\(d(u,v)=1\)
\(d(u,v)=1\)时,u、v之间有一条边,由于图G是2连通的,所以这条边不是桥。
因此,结论显然成立。 -
假设\(d(u,v)<k\)时结论成立,往证\(d(u,v)=k\)时成立。
【定理2】

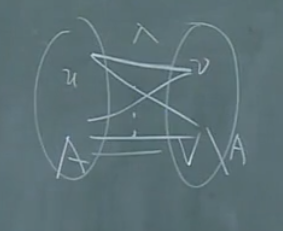
这个结论启发了明格尔研究任给两个顶点,其不相交的路(独立轨)的最大条数的最小值,可以刻画图的连通程度。
注:最大独立轨的最小值是\(\kappa (G)\)。
明格尔定理
Menger's theorem
分离
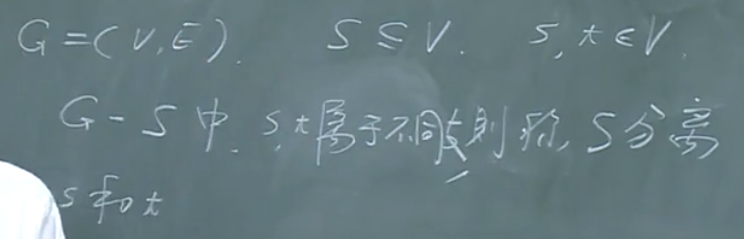
明格尔定理


柯尼希定理
Konig's theorem
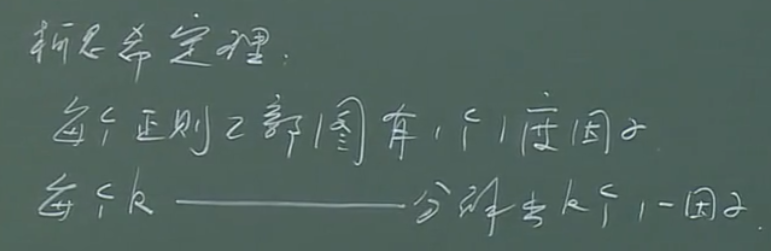
对连通度的研究(明格尔定理)与二部图匹配(柯尼希定理)联系起来了。
最大流最小割定理

对连通度的研究(明格尔定理)与网络流问题(最大流最小割定理)联系起来了。
网络流问题
算法设计与分析课程中会进一步讨论。
应用
自来水管道、运输网等一大类的组合优化问题。
模型
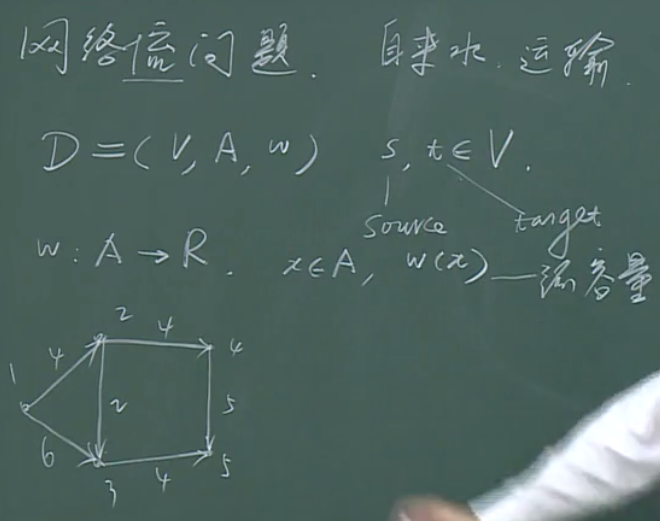
图D是一个有权的有向图,称之为容量网络。
试问从s到t的最大流量是多少?
术语介绍:
流量:在网络中实际流动的值,标有的权值视为容量;
网络流:不同弧上的流的集合;
可行流:满足容量约束(限制条件)与s流出与t流入相等(平衡条件)这两个约束的流;
零流:
伪流:满足限制条件不满足平衡条件的流;
最大流:可行流上的流量总和的最大值;
饱和弧:流量与容量相等的弧;
不饱和弧:
链:不考虑方向的路;
增广路:满足如下条件的链:
1、前向弧不饱和;
2、后向弧不为零。
残留流量:容量减去实际流;
残留网络:残留流量的网络;
割:使图不连通所去掉的最小顶点;
割边:去掉的边的集合;
割容量:割边集合容量之和;
最小割:容量最小的割。
定理
增广路定理:

最大流最小割定理:

与明格尔定理等价。
例子
网络流问题两种常用方法:

Ford-Fulkson方法、Push-Relabel方法(假设s处对网络加压,进而重新标记容量的方法)。
【例】
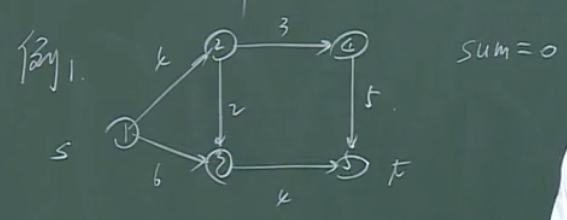
初始时刻,流量均为0(\(sum=0\))。
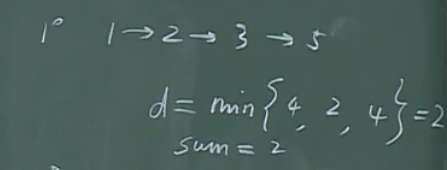
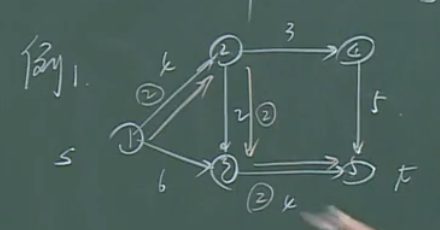
第一次迭代后,残余流量如上图所示。
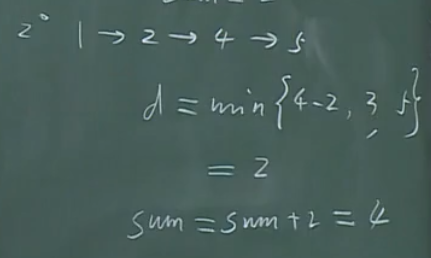

……
如此迭代,最后得出的最大网络流为7。
匹配问题
匈牙利算法(Hungarian algorithm)是求一个图的最大匹配的算法。
那什么是匹配呢?
独立集与团
独立集:
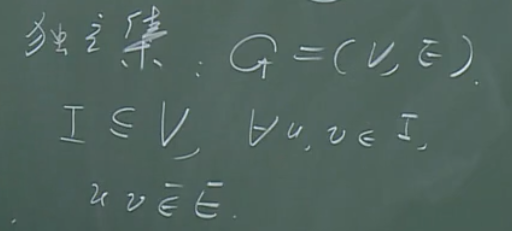
最大独立集:
所有独立集中,其顶点个数最多的称为最大独立集。
如何求最大独立集?
可使用简单的搜索法(求出所有独立集,再加以比较)。
当然,简单搜索法并不是一个好的算法。
求最大独立集是一个NPC(NP完全问题),很难找出好的算法加以解决。
P问题、NP问题、NPC问题、NP
P问题(Polynomial)
P问题,由其名字(Polynomial)我们不难看出它指的就是能在多项式时间内解决的问题,亦即解决这个问题的算法的时间复杂度是是多项式。
NP问题(Non-deterministic Polynomial)
在多项式时间内可判定其答案是否正确的问题。
也就是说,不能判定这个问题是否能在多项式时间内求得其解,但是对于这个问题的一个解可以在多项式时间内证明是否正确的。
即该问题的求解过程是不确定的,而对其某一个解的验证则能够在多项式时间内完成。
因而显然P类问题是NP问题的子集,因为倘若一个问题可以在多项式时间内被求解,那么这个解也一定可以在多项式时间内被验证是否正确。
NP问题的另一个定义是,可以在多项式的复杂度里猜出一个解的问题。
NP完全问题(NPC问题,NP-Complete问题)
存在这样一个NP问题,所有的NP问题都可以规约成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。
(1)同时满足:
- 得是一个NP问题;
- 所有的NP问题都可以约化到它。
(2) 举例
旅行商问题和集合覆盖问题都是NP完全问题。
(3)如何识别NP完全问题- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是NP完全问题。
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
- 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题。
- 如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题。
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
NP-Hard问题
NP-Hard问题是这样一种问题,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广,NP-Hard问题没有限定属于NP),即所有的NP问题都能约化到它,但是他不一定是一个NP问题。
NP-Hard问题同样难以找到多项式的算法,即使NPC问题发现了多项式级的算法,NP-Hard问题有可能仍然无法得到多项式级的算法。
事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。
很显然,所有的P类问题都是NP问题。也就是说,能多项式地解决一个问题,必然能多项式地验证一个问题的解――既然正解都出来了,验证任意给定的解也只需要比较一下就可以了。
关键是,人们想知道,是否所有的NP问题都是P类问题(注意:跟“所有的P类问题都是NP问题”表述的顺序是不同的)。
我们可以再用集合的观点来说明。如果把所有P类问题归为一个集合P中,把所有 NP问题划进另一个集合NP中,那么,显然有P属于NP。现在,所有对NP问题的研究都集中在一个问题上,即究竟是否有P=NP?通常所谓的“NP问题”,其实就一句话:证明或推翻P=NP。
从NPC定义上看,所有的NP问题都能约化成NPC问题,那么只要任意一个NPC问题找到了一个多项式的算法,那么所有的NP问题都能用这个多项式复杂度算法解决了,同时,P问题也是多项式复杂度算法解决的,所以NP也就等于P了。因此,给NPC找一个多项式算法太不可思议了。那么,前文说,“正是NPC问题的存在,使人们相信P≠NP”。我们可以就此直观地理解,NPC问题目前没有多项式的有效算法,只能用指数级甚至阶乘级复杂度的搜索。
团:
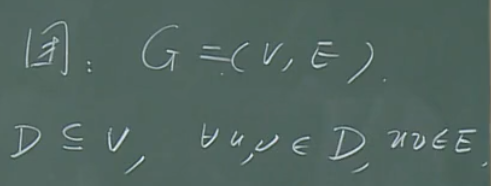
由于其对称性,求最大团问题也是NPC问题。
求最大团问题的现实意义是什么?
求最大团的现实意义:
物以类聚,人以群分。
团的意义在于寻找具有相同点的一群事物,进而精准实施某种操作。
匹配/边独立集:

偶图匹配问题

完全匹配与完美匹配:
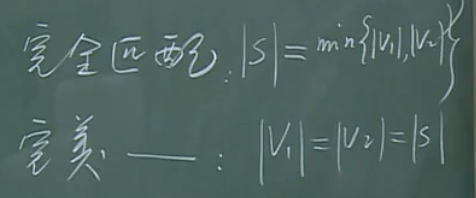
完美匹配即为正则二部图。
偶图匹配的条件
【定理1】Hall结婚定理(Hall's Marriage Theorem)



【证明】

相异代表系(匹配问题的另一种数学描述方法)
相异代表系的概念:
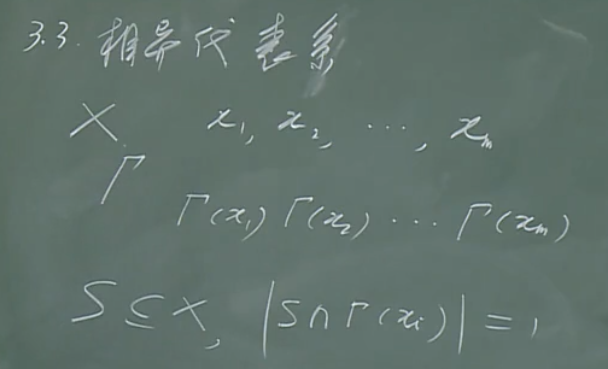
\(\Gamma (x_i)\)是\(x_i\)的映射,可以理解成结婚问题里面的对象列表。
相异代表系就是取出X的一个子集S,并同时从每个\(x_i\)的映射中取出不相同的一个。
霍尔定理:
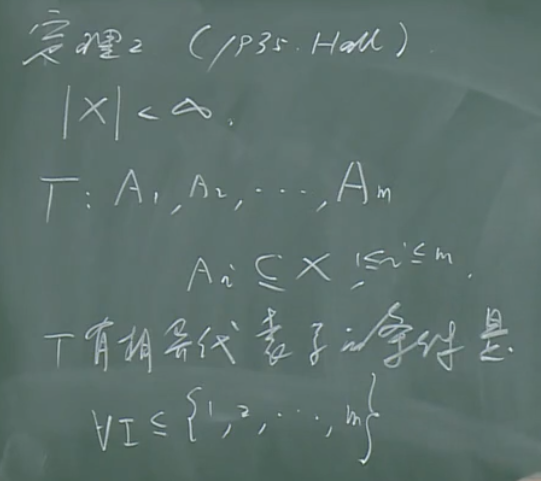

这是一种纯数学的描述,其实质与霍尔结婚定理是一样的。
结婚问题的变形

第一种是指,例如招工,一个公司所招人数超过一人。
第二种可以联想员工跳槽。

1962年,Gale-Shapley algorithm,“GS算法”,也称为 “延迟接受算法”(deferred-acceptance algorithm)。
2012年的诺贝尔经济学奖,来自哈佛大学商学院的Alvin Roth和UCLA的Lloyd Shapley分享了今年120万美元的奖金,以此表彰他们对Gale-Sapley算法的提出和改进所作的贡献。
瑞典皇家科学院表示,此次的诺贝尔经济学奖是对于“稳定分配(Lloyd Shapley)及市场设计实践理论(Alvin Roth)”的认可。
几个概念
点覆盖:

边覆盖:
类似的,可以定义。
支配集:


最小支配集越少越好。
实例:微信公众号
支配集也分为顶点支配集和边支配集。
二分图的性质

平面图与顶点着色
平面图与欧拉公式
背景
【例子1】
印刷电路板的交叉线路不能放在同一个平面
【例子2】
道路地下管道的不同系统交叉管线不能放在同一个平面
平面图、可平面图、面
可平面图:

平面图:

注意二者的辨析:
平面图是已经画在一个平面上且各边除顶点外不相交的图,可平面图是可以画在一个平面上且各边除顶点外不相交的图。
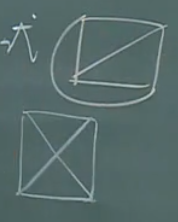
上图为平面图,下图为可平面图。
面:

给定一个图一定有面。这是因为一定有外部面,如下图所示:

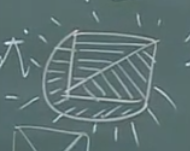
面的典型特征是什么?
由于面是由一个圈(内部不能有边)围成的不能再分割的区域,所以这个特征是圈的长度。
欧拉公式
欧拉最早从凸多面体来研究平面图的。
凸多面体定义:
任何一个面,将多面体延展后,其他所有面均在该面的一侧。
【定理】欧拉公式

【证明】
由于没有已有的结论与要证的结论接近,所以我们使用数学归纳法证明。
施归纳于f。

每个面都是圈围城的,由于此时\(f\ge 2\),因此,一定有一个内部面。
我们可以去掉这个内部面,去掉之后根据归纳假设满足该公式。
由于去掉圈中的一条边就可以破掉这个圈(生成树一节的破圈法),所以在归纳假设的式子中,q与f同时加一即可证明。
【实例】

根据右图,可以得到左侧的关系式。
注意的是,式2由握手定理得出,式3的理解要注意每条边参与构成两个面。
【推论1】
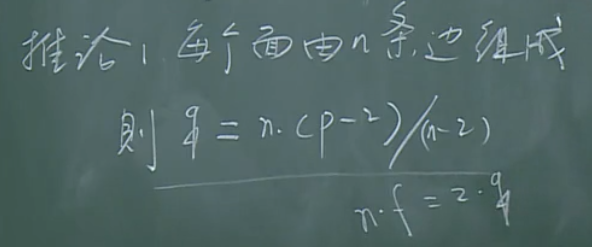
【推论2】

最大的意思在于,对于面来说,这是最大平面图。也就是说,如果再加一条边,就不再是平面图。
【推论3】

推论2、3都是由推论1令n为不同的值得到的。
【推论4】

注意:偶图(双图)中没有三角形,但是没有三角形的图不一定是偶图。
【推论5】

【证明】

【推论6】
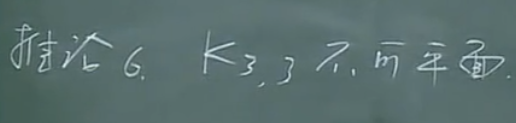
【推论7】
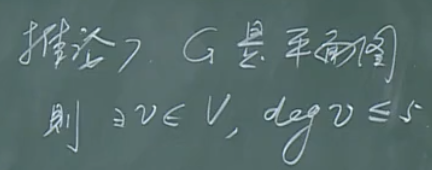
这个推论对证明五色定理有用。
【证明】
反证法。
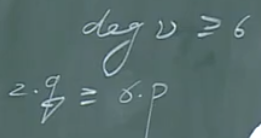
例题
【例1】
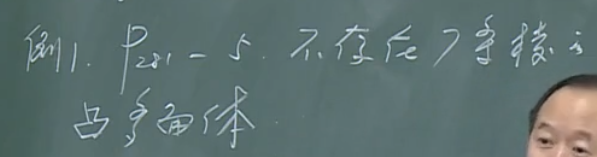
【证明】
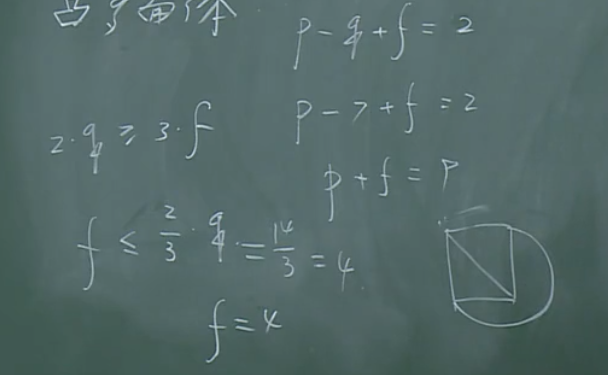
【例2】

【解】
\(q=6\)是满足条件的。也即三棱锥。
【引申】
证明\(q\ge 6\)且\(q\neq 7\)时,均存在q条棱的凸多面体。
【证明】
8条棱:

与之类似的,10条棱只需将底面变成5边形。
故偶数棱均可。
那么奇数棱呢?
自主证明。
非平面哈密顿图
Grinberg定理
【定理】
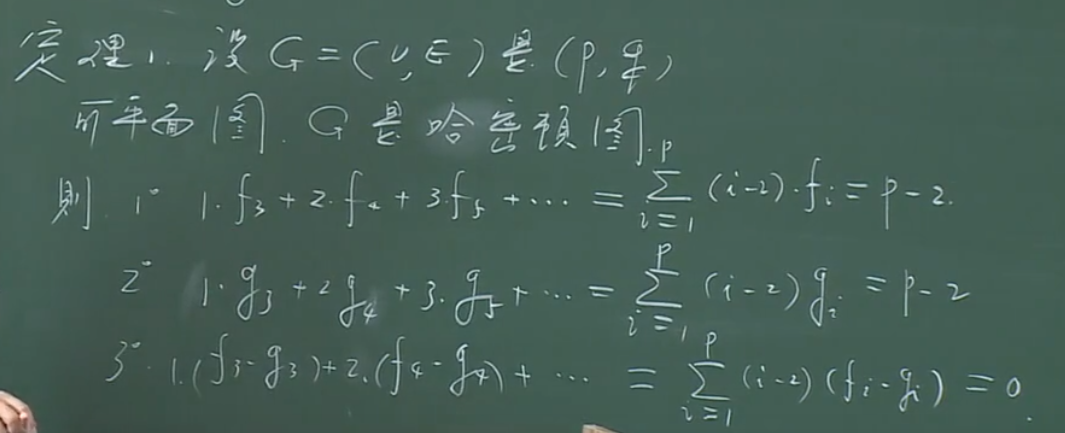

【解释】

如图,红色为哈密顿圈。此图中\(f_4=2\)、\(g_4=1\)。
【证明】
由于3式为1式减2式所得,故无需证明。
另由于1式、2式具有高度对称性(这也说明,哈密顿圈内外具有对称性),故可仅证1式。
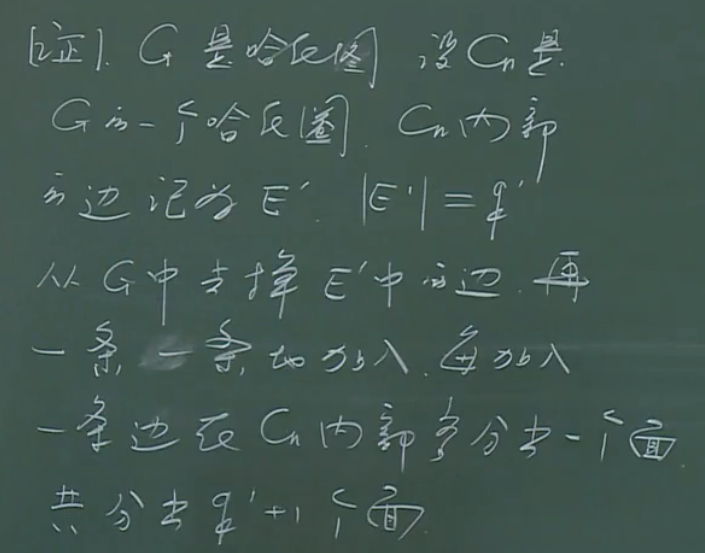
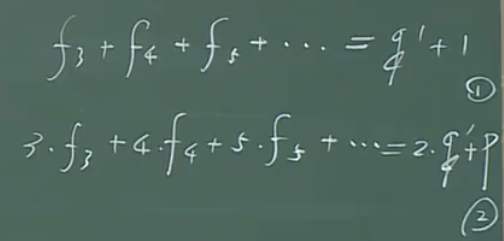
式2是由面上边的和是边数的2倍所得到的,+p的原因是因为哈密顿圈上的边参加形成面且仅参加一次。

应用
【例】
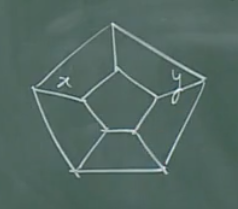
证明x、y不能在一个哈密顿圈上。
使用Grinberg定理判断一个图是不是哈密顿图依然是比较复杂的,但是相比于寻找有无哈密顿圈的方法,已经简便很多。
图的着色
顶点着色
相关术语
n-可着色:用n种颜色可着色。
色数:最小的n。
对应到考试安排上,就是考试时段。
但是,求色数是NPC问题。
有算法:用一种颜色染尽可能多的点,换一个色继续,直到完成(简单的贪心算法)。没有好的算法。(目前)
【例】
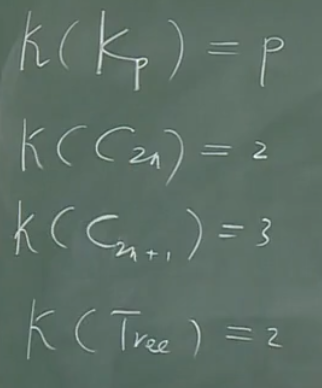
注意:树是一种典型的层次结构,色数为2。
边着色
使用较少,不再赘述。
色数的上下界
下界:

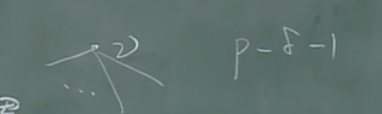
上界:
【定理1】

【解释】
可以简单地用数学归纳法证明。

去掉这个顶点,归纳假设剩下的顶点均可着色(仅用了\(\Delta (G)\))种颜色。
对刚才去掉的顶点,用另外的一种颜色着色即可。
【定理2】
\(G=(V,E)\)是平面图,则其是\(\Delta (G)\)可着色的。
【定理3】
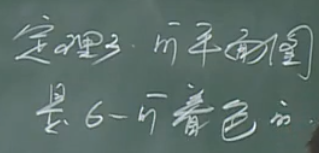
【证明思路】
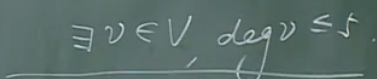
利用这个结论,用归纳法证明。
四色定理VS五色定理
五色定理
【定理】
任何一个平面图都是5-可着色的。
【证明】
施归纳于p。
考虑\(\mbox{deg}\ v\le 5\)的那个顶点:
-
\(\mbox{deg}\ v\le 4\)
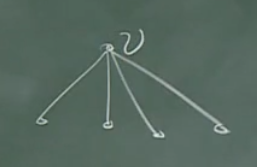
由归纳假设,除v外的顶点已5-着色。而与v邻接的顶点最多只有4个,最多用去4种。得证。 -
\(\mbox{deg}\ v=5\)
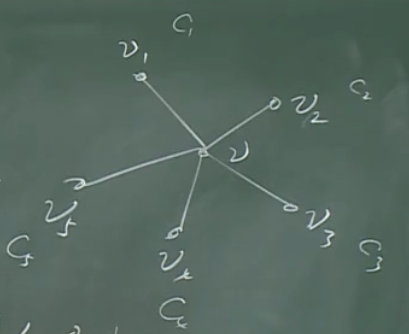
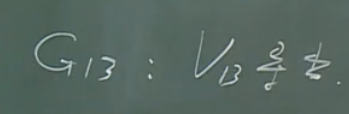
其中,\(V_{13}\)是指用\(c_1\)、\(c_3\)两种颜色染色的顶点集合,\(G_{13}\)是其导出子图(两个顶点都在\(V_{13}\)中的边才算在内)。-
\(v_1\)、\(v_3\)不在一个支
这样的话,我们在\(v_1\)所在的支里面将\(v_1\)改染\(c_3\)。
节省出的颜色用于染v即可。 -
\(v_1\)、\(v_3\)在一个支
在这种情况下,\(v_2\)、\(v_4\)必不在一个支。
原因是,如果\(v_1\)、\(v_3\)在一个支,\(v_2\)、\(v_4\)也在一个支,则这就不是一个平面图了。为什么???
用类似的方法对\(v_2\)、\(v_4\)操作,即可证明。
-
有向图
无向图与有向图的对比
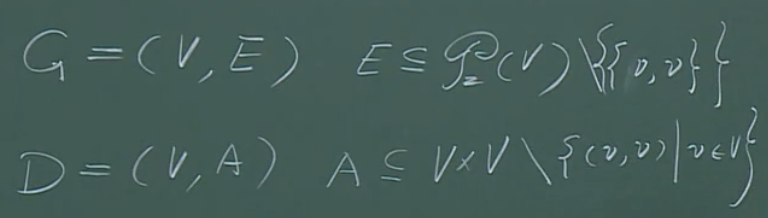
有向图不具有对称性。但是,无向图的理论可以为有向图的研究提供指导。
【例】

如果边上没有方向(也就是对于无向图来讲),这样是不符合定义的。
但是对于有向图,这样是符合定义的。
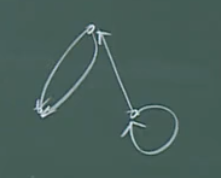
但是必须注意的是,这样的图(具有多重弧以及带环顶点)对于有向图也是不符合定义的。
这种称为有向图中的伪图。
基本概念
有向图
【定义】
与无向图类似,另注意有向图的边可以称为弧。
有向图的表示
-
用定义表示
列出V与A两个集合。
-
图解法
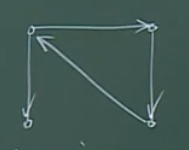
-
邻接矩阵法
-
关联矩阵法
计数问题
p个顶点能构成的图个数:
无向图:
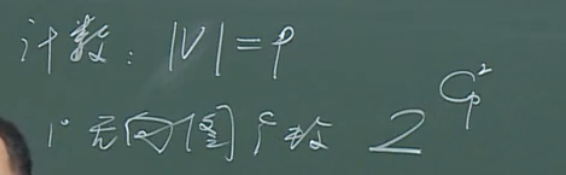
注意:
\(C_p\)是p个顶点构成的集合,\({C_p}^2\)是p个顶点构成的二元集合。
有向图:

也即在所有笛卡尔乘积中去掉自反的那些。
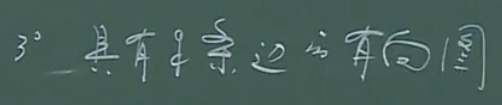

伪图
定向图

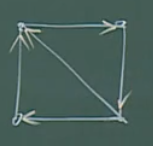
下图称为上图的定向图。
例:单向道
度
【定义】

握手定理
对于无向图:
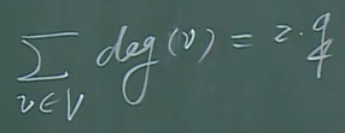
对于有向图:

注意:无向图中的握手定理在有向图中仍然成立,但是在有向图中此式更有作用。
有向完全图
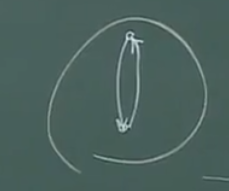
这就是一个有向完全图。
【定义】

注意:
在无向图中,满足\(G+G^c=K_p\)。
在有向图中,依然存在这样的关系,也即\(D+D^c=p阶有向完全图\),其中\(D^c=V\cup A^c\),而\(A^c=V\times V\backslash \{v,v\} \backslash A\)。
同构
【定义】
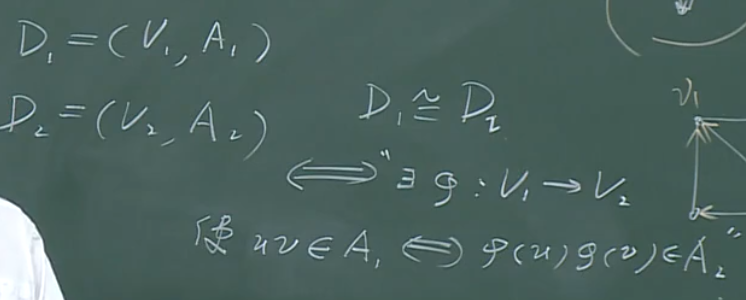
怎么找同构,在有向图中仍然是一个NPC问题。
有向路与有向圈
路的重要性在于它是用来描述图是否连通的工具。
有向通道与闭有向通道
与无向图中类似。
有向迹与有向闭迹
边不能重复的有向通道。
有向路
顶点不能重复的有向通道。
有向闭路(有向圈)
有向图的连通性
可达
【定义】

这个关系R是自反(u与u自身之间可达)和传递的。
但是不是对称的。
相互可达
在关系R的基础上具有对称性即为相互可达。
连通性
弱路与弱连通
弱路:不考虑路的方向条件下的路。
弱连通:任何顶点间有一条弱路。
单向连通
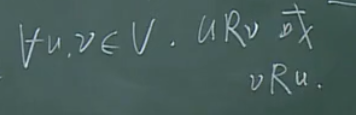
强连通
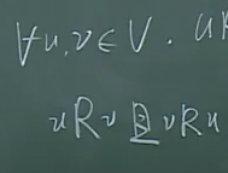
互达
对于u、v直接的这种关系R,我们定义为:
互达:\(R_D\)。

这个关系是自反、传递以及对称的(这是个等价关系)。
等价关系可以用来对事物进行分类,分类后可以用其中一个来代表。(即划分)
强支(极大强连通分量)
强支的概念
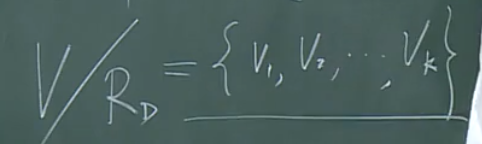
对V利用\(R_D\)关系确定一个划分,称为V相对于\(R_D\)的商集,记作\(V/R_D\)。
而这个商集正好是该等价关系的等价类的集合,该集合则是V的一个划分。
该划分中的任一个等价类\(V_i\),则其是V的一个子集。
因此,可以通过\(V_i\)导出一个子图,称之为强支,也称为D的极大强连通分量。
极大的原因在于,\(R_D\)是一个等价关系,与\(V_i\)中任一个顶点等价的其他顶点,全部在\(V_i\)之中。
利用邻接矩阵求强支
引入:
在无向图中,给定的两个顶点之间,我们可求其长为r的通道的条数。
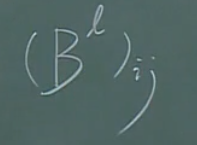
其中,B是邻接矩阵。
有向图的通道数:
在有向图中,此方法亦然。
可达矩阵:

求强支:
\(R\wedge R^T\)。
对\(v_i\)行中,其列为一的列标记为\(j_i,\cdots ,j_k\)。
其中,对应着顶点集\(v_{j_1},\cdots ,v_{j_k}\)。
这个顶点集的导出子图,则为\(v_i\)所在的强支。
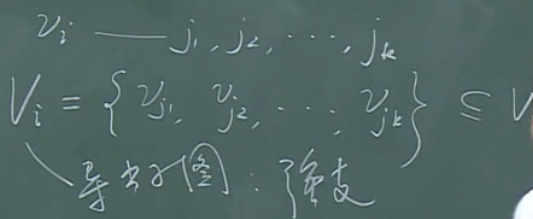
应用
有向无环路的拓扑排序
有向无环路(DAG,Directed acyclic graph),无环指不存在有向圈。
【实际场景】
例如选课时的先修课程要求,
做饭时的工序要求等。
【例】

【命题】
这幅图中,一定有一个顶点入度是零。
【证明】
有穷系统中一定有最长路,其起点入度是零,终点出度是零。
【问题描述】
假设有四道工序,1决定3能否进行,2决定4能否进行。
因此,需要合理的排序(拓扑排序)。
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
一种实现的算法为从中找出入度为零的顶点,将其排在第一个并在图中删去它。
剩下的仍有入度为零的顶点,如此循环处理。
寻找入度为零的顶点可以简单地使用遍历法。
大规模任务的分布式处理的流水式并行法也与之类似。
操作系统的资源分配图
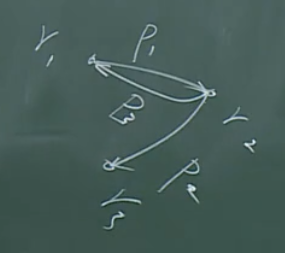
弧上的字母表示进程名,代表该进程正在使用起点的资源,而需要申请终点的资源。

如图所示,即出现了死锁问题。(以图论的观点,是出现了强支。)
早期操作系统为避免死锁问题,采用了一系列的方法:
- 进程优先级
- 操作顺序
但是这些方法造成了系统灵活性的丧失。
交通控制
与图的定向问题有关。
1939年,Robbin给出一个结论:
只要该无向图是一个没有桥的连通图,则一定有它的一个定向图是强连通的。
但是,这个结论没有考虑所产生的距离代价(有可能你到一个很近的地方,需要绕很远的路)。
有根树、有序树
有向树
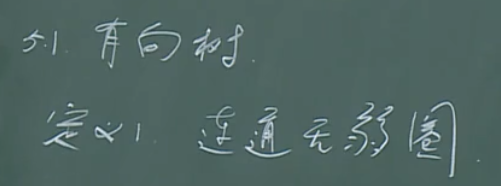
有根树
【定义】

有根树的叶子:
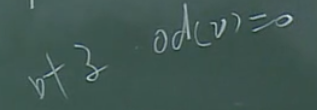
有序树
有序树是指一类特定的有根树,其兄弟节点之间也是有序的。
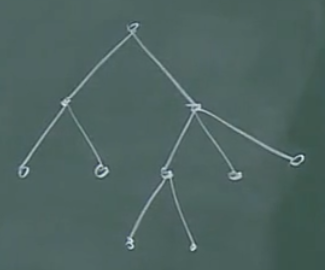
-
树是分层的。
-
深度。
即所处的层数,第一层的深度为0。
-
高度。
高度是指总层数。
m元-正则树
每个顶点的出度不是m就是0。
例如,2-正则树:
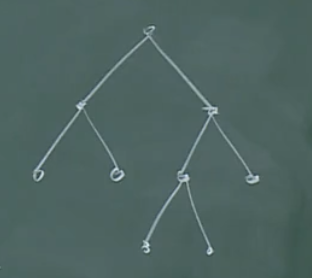
满2-正则树:

【例1】
2元-正则树,有\(n_0\)个叶子,能否求出其有几个顶点几条边?
【解】
虽然是有向图对应的有向树,其无向图无向树中的理论仍然成立,则有\(p=q+1\)成立。
另外,对于\(n_0\)个叶子,其出度均为0,而其他节点的出度均为2。
依次可以求出。
【例2】
数学语言描述的算术表达式,如何让计算机理解呢?
应该形成一个抽象的语法树表达。

与有向无环路(DAG)的关系:
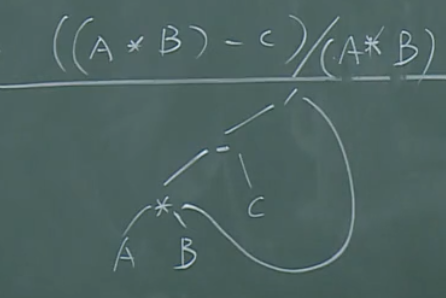
注意:
这个图在有向图中是无环的,当然其在无向图中有环。
因此,对其进行拓扑排序,即可得出生成其机器指令的顺序。
使用DAG的好处在于,对于相同的子表达式,只需生成一次。
完全二元树
“完全”不代表其是满的。
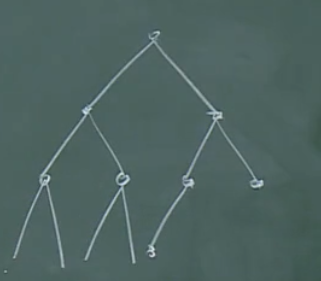
任意给定一个树,均可转化为二元树。
二元树作为数据结构,则具有广泛的可用性。
完全二元树是特殊的有根树、有序树,其倒数第二层一定是满的,且最后一层全部靠左,从完全二元树可以得到堆。
堆相比于完全二元树,又多了一种“序”,其每个节点的子节点,要么比该节点大,要么比该节点小。
这样就避免了排序,大大提高了算法效率。
最短路径、最小生成树在堆上进行,可以得到更好的算法。
在数据结构中将进一步探究。
比赛图
引入
完全图的定向图就称为比赛图。
其方向取决于“比赛”的胜负结果。
定理
【定理】
比赛图中一定存在一条哈密顿路。
【证明1】数学归纳法

只关注如何利用归纳假设。
我们寻找最后一个向新增加顶点指的弧,可以轻松地得到更长的哈密顿路。

【证明2】最长路
比赛图里的最长路就是哈密顿路。
使用反证法。
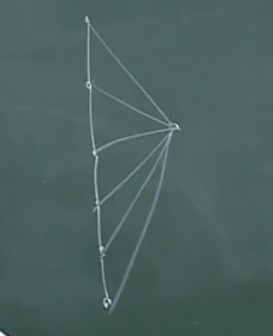
【例1】
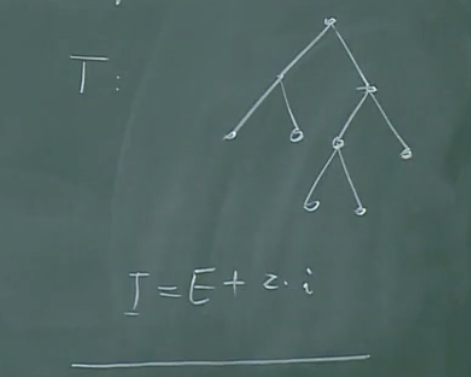
对于这样的一个正则二元树,有\(I=E+2i\)成立。
其中,I是叶子顶点的深度和,E是内定点的深度和,i是內顶点(非叶子顶点)的个数。
【证明1】数学归纳法
注意:
对于有根树来说,归纳假设要注意需要去掉的是其根节点。
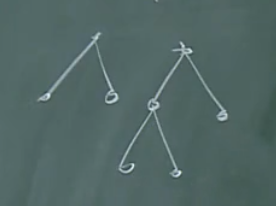
也就是说,归纳假设必须写成第二归纳法的形式。
而加上最上方的内顶点之后,只是多了一个内定点与两条边,易证结论成立。
【证明2】
对于内节点来说,其出度均为2,因此,2i刚好是其边数。
也就是说,所有叶子节点的深度总和,等于内节点的深度总和加上边数。
因此,如果对于任一条边,可以证明结论成立的话,则可以认为结论证得。
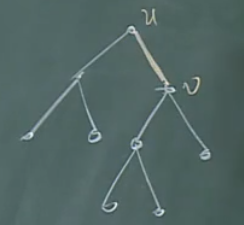
对于边uv,v的子树其内节点正好为叶子节点减一。
其正好差一条边???
【例2】
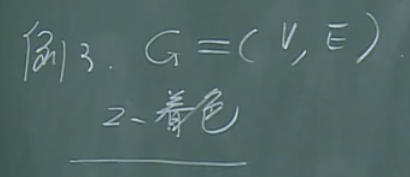
注意:不是2-可着色,也就是说仅仅是用两种颜色对其顶点进行染色,并不严格要求两个邻接顶点颜色不同。
其现实意义:
比如黑人白人合住小区,能否保证黑人的白色邻居多,白人的黑色邻居多?
【例2的不同描述】
把一些人组成一个团体,把这些人分为两组,使每个人在自己组内的朋友数至多是整个团队朋友数的一半。
即对V进行一个划分,
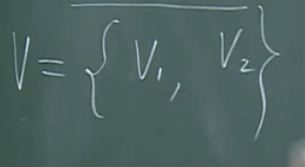
使如下数目最大:

启示:
学会从不同角度思考问题,
甚至从不同角度得到的问题可能是相同的。
【完】



 浙公网安备 33010602011771号
浙公网安备 33010602011771号