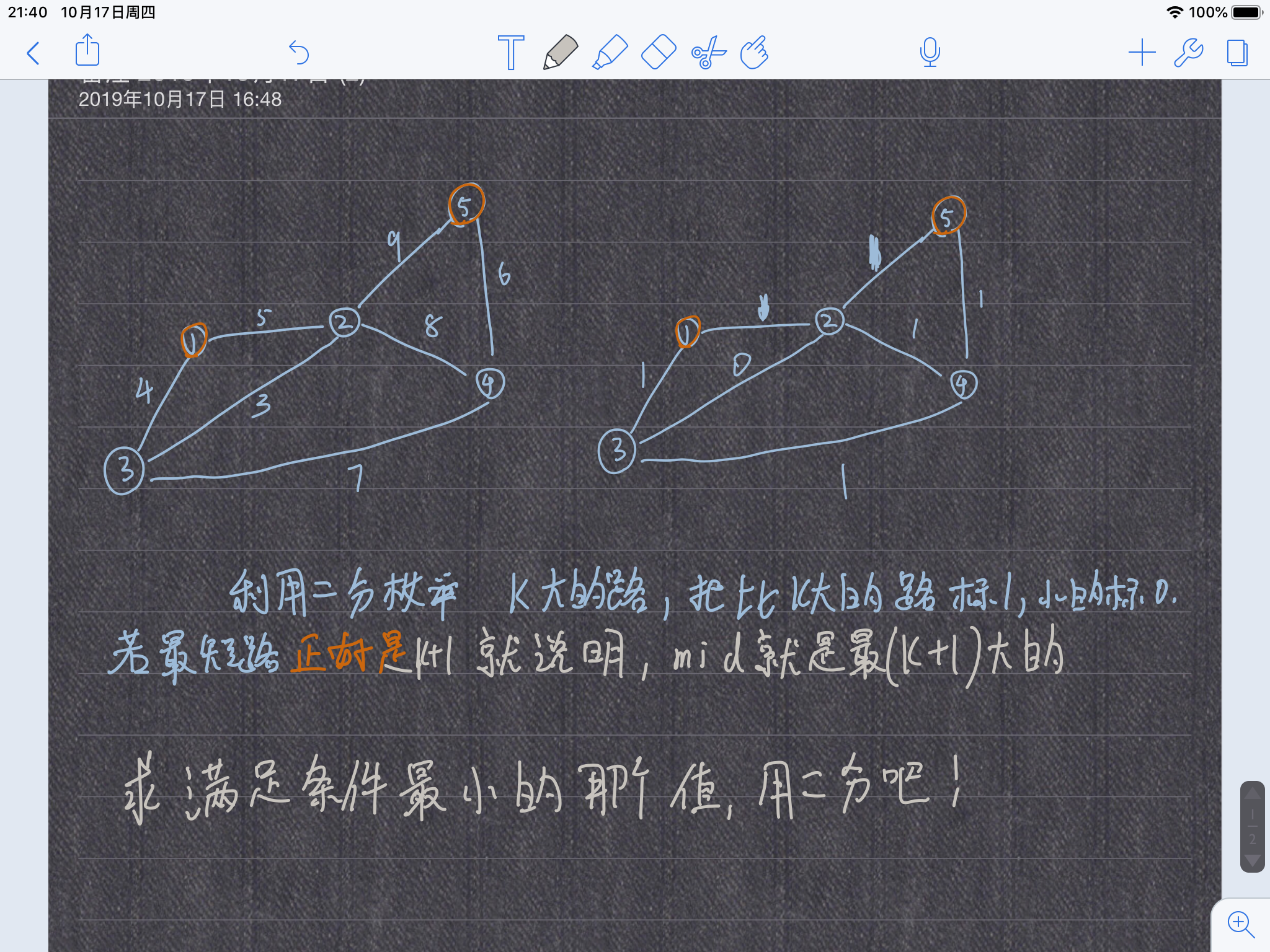
在加权无向图上求出一条从1号结点到N号结点的路径，使路径上第K+1大的边权尽量小

二分+最短路算法

 

 

 

 

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#define maxn 100010
using namespace std;
const int INF = 0x3f3f3f3f;
struct Node {
	int p;
	int len;
	Node(int a, int b) :p(a), len(b) {}
};
vector<Node>G[maxn];
void insert(int be, int en, int len) {
	G[be].push_back(Node(en, len));
}
bool operator <(const Node a, const Node b) {
	return a.len > b.len;
}
int vis[maxn];
int dis[maxn];
int n, m, k;
int dijstra(int be, int range) {
	memset(vis, 0, sizeof(vis));
	memset(dis, INF, sizeof(dis));
	priority_queue<Node>que;
	que.push(Node(be, 0));
	dis[be] = 0;
	while (!que.empty()) {
		Node ans = que.top();
		que.pop();
		if (vis[ans.p]) continue;
		vis[ans.p] = 1;
		int x = ans.p;
		for (int i = 0; i < G[x].size(); i++) {
			int p = G[x][i].p;
			int len;
			if (G[x][i].len >= range) len = 1;
			else len = 0;

			if (dis[p] > dis[x] + len) {
				dis[p] = dis[x] + len;
				que.push(Node(p, dis[p]));
			}
		}
	}
	return dis[n];
}
int check(int mid) {
	int len = dijstra(1, mid);
	if (len >= k + 1) return 0;
	else return 1;
}
int main() {
	int be, en, len;
	scanf("%d%d%d", &n, &m, &k);
	for (int i = 0; i < m; i++) {
		scanf("%d%d%d", &be, &en, &len);
		insert(be, en, len);
		insert(en, be, len);
	}
	int l = 0;
	int r = 10000000;
	int mid;
	int flag = 0;
    
	while (r - l > 1) {
		mid = (r + l) / 2;
		if (check(mid)) {//往小了压
			r = mid;
		}
		else {
			l = mid ;
		}
	}
	if (r == 10000000) cout << "-1" << endl;
	else cout << l << endl;
	return 0;
}