吴恩达机器学习笔记 - SVM

001. SVM的优化目标及损失函数

　　跟其他直接从margin出发不同，这里从Regression 的交叉熵损失函数引入，对sigmoid函数做了一点近似的拉直变形，直接引出了SVM的损失函数

 

 

 　　

 

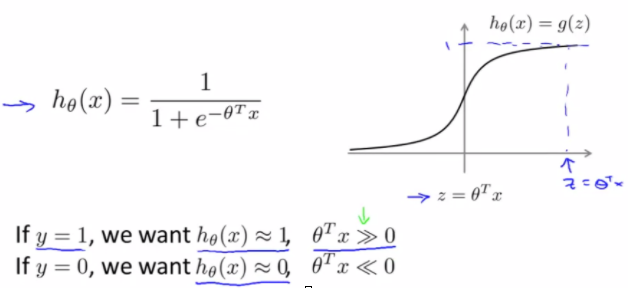
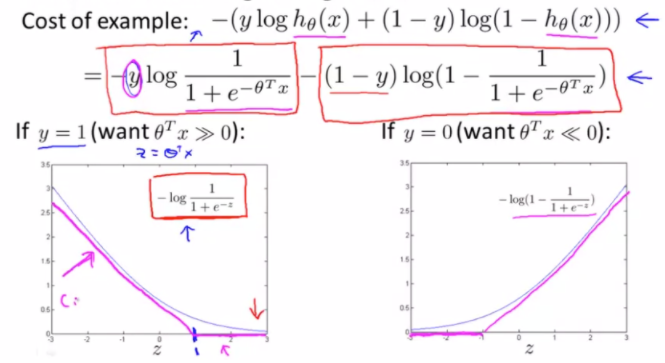
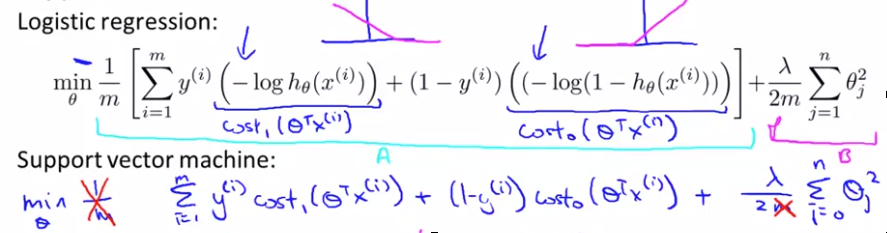
002. 大间隔的最优解

　　有超参数C开始讨论，当C 足够大时，要minimize目标函数，则需要 第一项等于0，这样就将无约束的优化，转化成了有约束的优化，及SVM的决策边界。　这一步可以看做是SVM求解过程所用到的拉格朗日乘子法的逆理解过程。

 

 

 

 

 

 

 

 

 

 

 

003.最大间隔的数学解释

　　将约束条件理解为 （ 样本到超平面法向量上的投影） * （法向量的模）

 

 

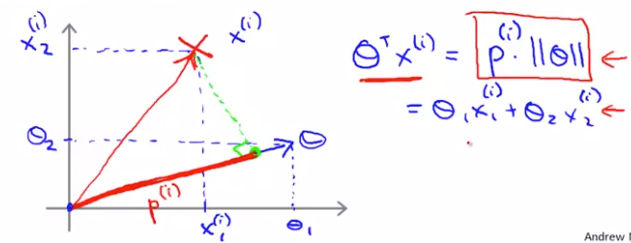
且优化目标函数理解为 法向量模的平方

 

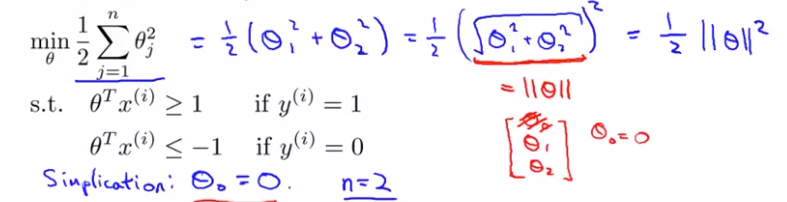
（ 样本到超平面法向量上的投影） * （法向量的模）>=1 的情况下， 投影越大，则法向量模及目标函数可以越小。 因此可以转换为找到 “法向量/超平面” 使得样本在其上的投影最大。

 

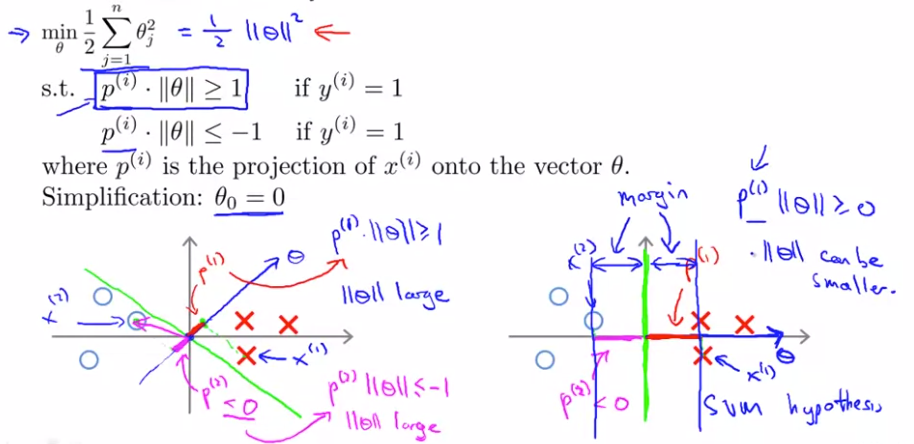
004. 核函数

　　非线性决策边界进行分类时，用多项式算法进行回归，需要计算很多高阶项，导致计算量很大

 

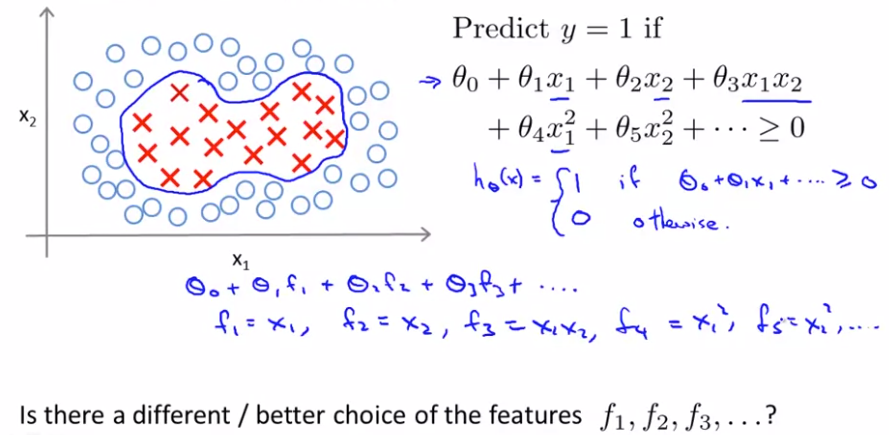
 这里寻找f1，f2，f3的另一种构造特征 - 高斯核方法

 

高斯核的可视化

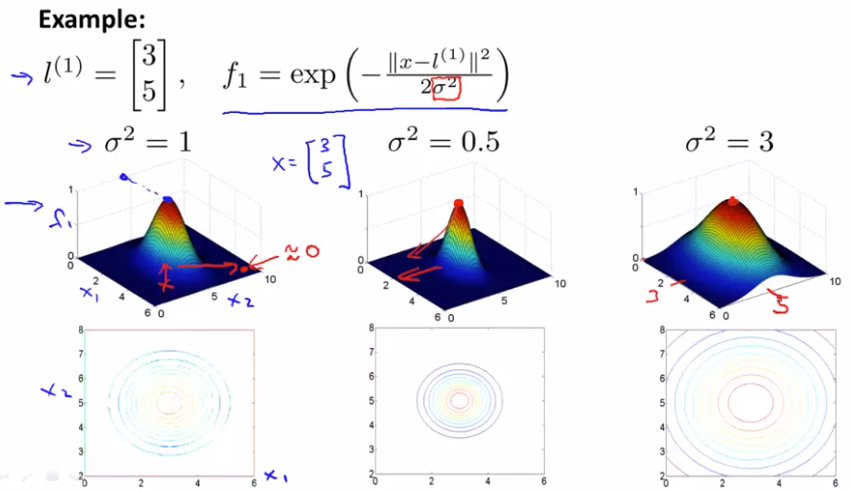
 以三点为核,通过lamda平方来控制范围，叠加求和以后将一个区域的取值提升趋近于1

 

 

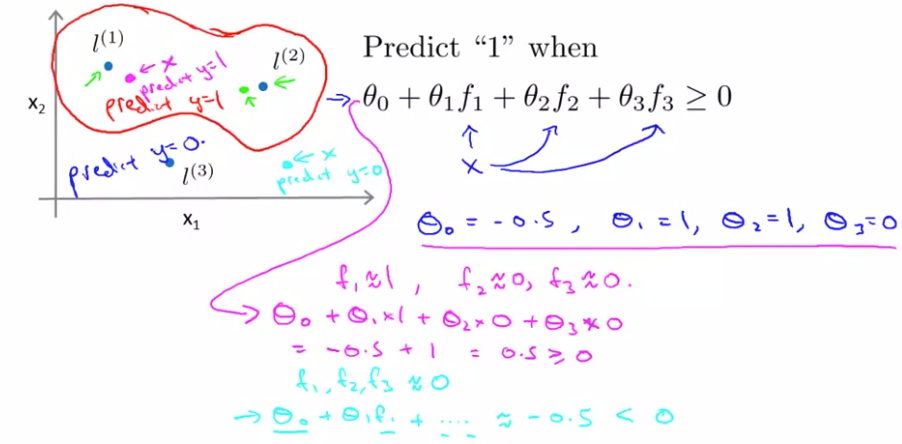
 005. SVM 核方法

　　对所有m个样本进行高斯核转换，每个样本Xi 映射到一个m+1维的特征空间F中，

 

 

 　　然后再利用线性SVM模型进行训练

 

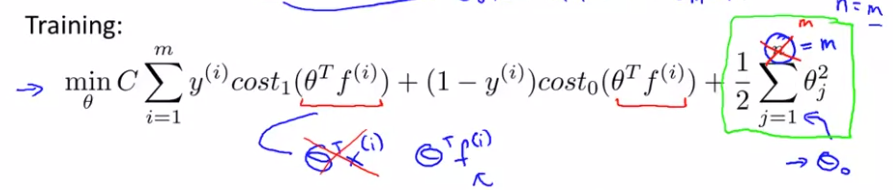
 　　补充： 核方法其实在其他的算法也可以嵌入做，比如逻辑回归，但是SVM计算过程中的tricks，并不能推广过去，因此计算会特别慢， 因此SVM跟核方法是相得益彰

 

 006. SVM 参数的设置

 　　C是正则化项lamda的倒数，因此C 越小，正则化参数越大，则模型bias 越高，variance越小

　　高斯核里面的lamda可以理解为影响了覆盖面， lamda越大，其覆盖面越大，越圆滑，因此实际模型的样本落入其中的概率大，variance就小

 

 　　结论：  overfit 时，降低C，加大高斯核lamda；

　　　　　　underfit时，增大C，降低高斯核lamda；

 

007. SVM的具体使用问题

　　　　核函数选择：

　　　　　　　　维数参数多，样本小，用线性核会合理点，因为高维容易过拟合；

　　　　　　　　维数参数少，样本多，用高斯核

　　　　　　　　

 

 　　用高斯核时，当特征的大小差异很大时，需要做归一化，否则在计算高维核特征时，较小特征范围得到的关注不够。

 

　　

　　其他核： 多项式核，String Kernels，Chi-square Kernels, Histogram intersection Kernels

 

 

　　线性核函数跟logistics regression经常拿来对比，因为算法比较相似（参考最开始的优化目标函数引进的过程），都适用于特征数量多，样本少的情形，且效果也往往也差不多

　　处理多分类问题时,跟logistics regression一样，采用one-all分类；

　　SVM的威力和魅力在于核函数对于复杂的非线性问题的处理上，样本量较大，特征数较多时，逻辑回归一般效果不好，而高斯核函数会十分突出

　　SVM的优化问题是一个凸优化，因此总是能找到全局最优解，无须担心local optima问题（在神经网络中，这是个不大不小的问题）

　　一般来说，在上面的各类样本量跟特征数上，神经网络都能取得不错的效果，但是问题是训练起来比较慢，比起SVM 会慢很多

　　不过，相对于在各类算法之间选择，实际上，在机器学习过程中，更加重要的是： 你有多少数据，你有多熟悉误差分析，debug算法调试，如何设计新的特征变量