IMU紧耦合优化——前篇

最近接手的项目要求做imu紧耦合的图优化，因此研究一下关于imu的知识
这篇文章写的会比较啰嗦，因为本人将致力于厘清遇到的每个知识点和数学推导

前置知识：李代数

在看slam十四讲和上老板课的时候就学过李代数，但认知一直停留在知其然不知其所以然的层面上，看了这个视频后感到豁然开朗：
https://www.bilibili.com/video/BV1xw4m1k7Sb/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=a024b504b5b18828fc2bd89aeee49995

(注意，以下仅为个人列举的重点，强烈建议至少倍速看一下上面的视频才能循序渐进地理解李代数)

1 - 直观认识李群李代数与流形的关系

流形引入了坐标图的概念，通过坐标图，我们可以把流形上的点用欧几里得空间中的坐标来表示。例如，对于地球表面这个二维流形，我们可以用世界地图来映射，这个例子描述了李群以及李代数的关系。

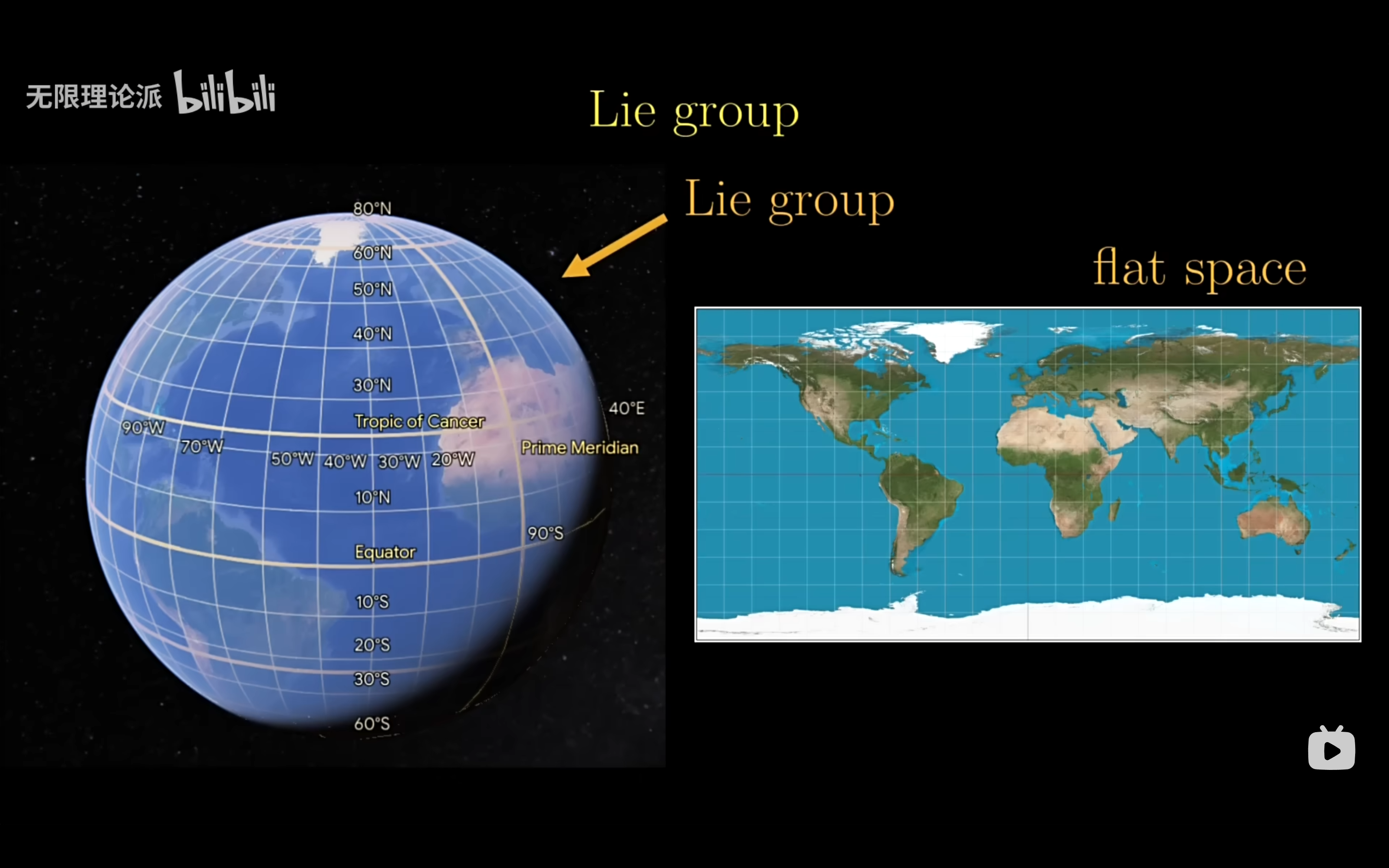
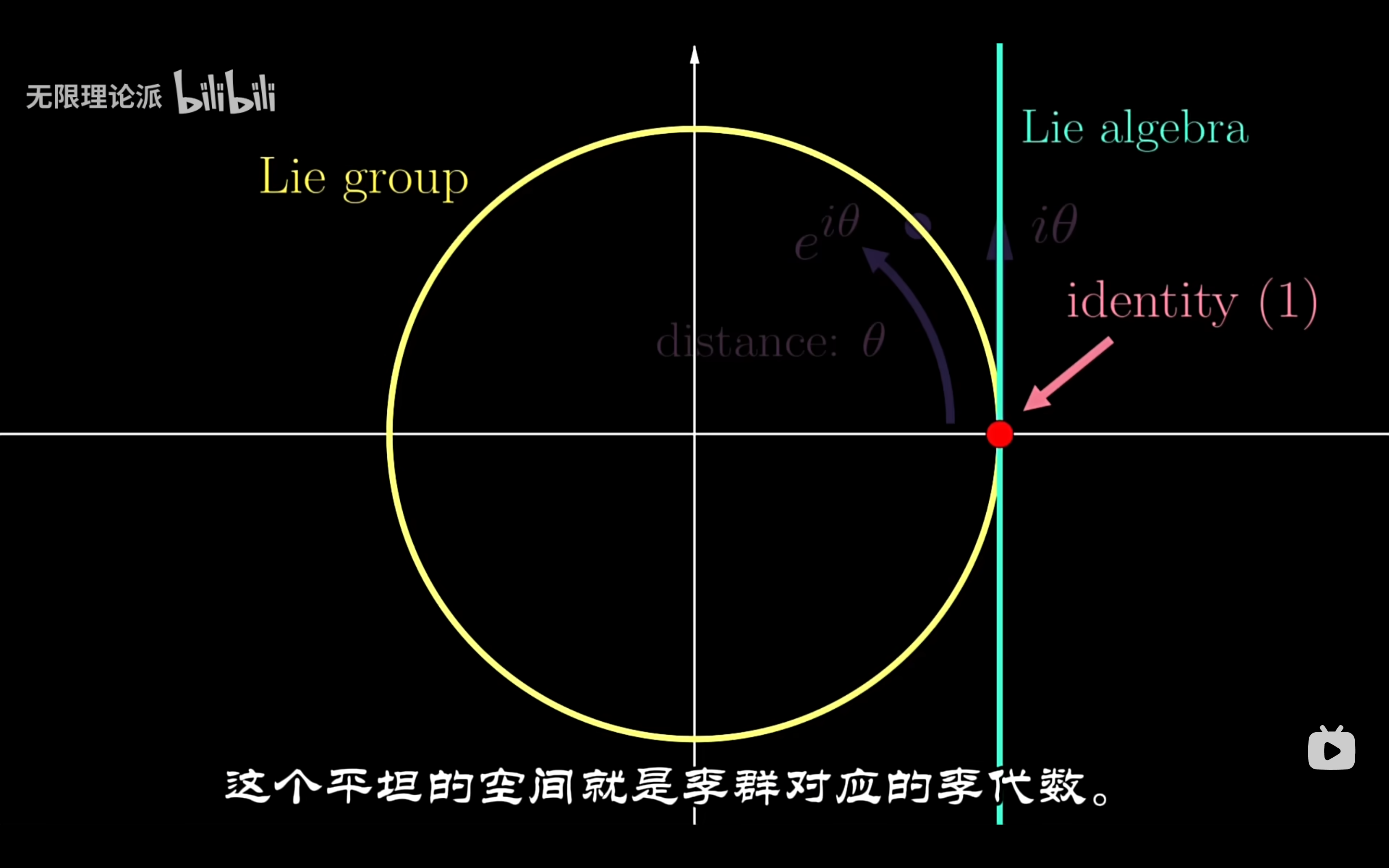
李群是一种复杂的弯曲流形，我们希望有一个平坦的空间来处理我们的坐标系，而这个平坦的空间就是李代数。

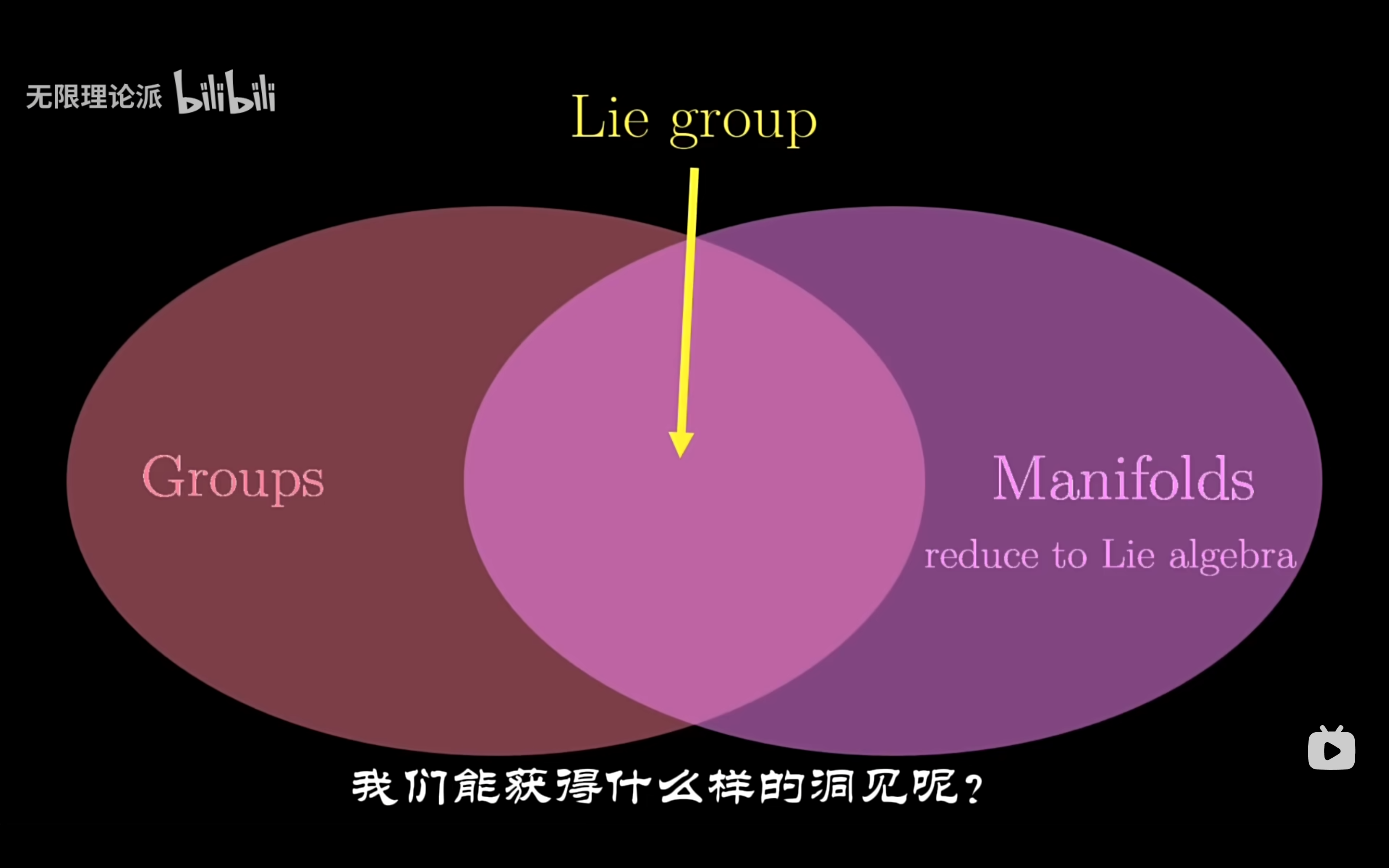
对于李群，找到了它的单位元素处的切空间，就找到了对应的李群李代数。

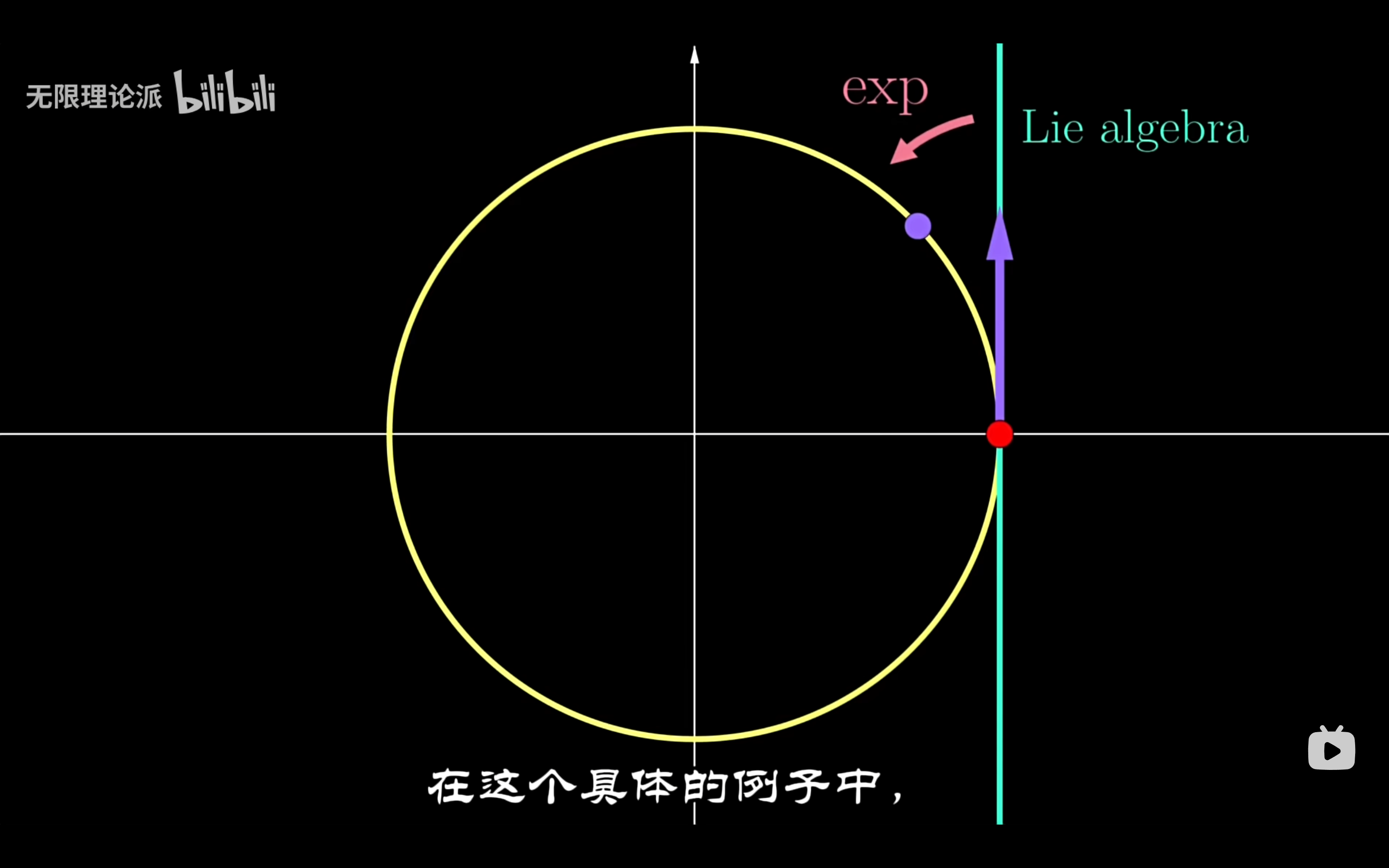
李代数作为坐标系的运作方式是：将切空间上的一个切向量“缠绕”在里群上，然后取终点。这种缠绕行为称为指数映射。

2 - 李群李代数的群性质

在李群中，最基本的运算是乘法，因此我们希望能把李群上的乘法转化为李代数上的操作。

李群的乘法到李代数运算的转化由一个无穷级数描述(BCH公式)，李括号可以被理解为一个简单但特定的操作，它将两个切向量转化为另一个切向量，使我们能够在李代数上完全复制群的乘法。

从群乘法的角度来看，我们可以只在平坦的李代数上进行操作，而不必处理弯曲的空间。

Q：为什么我们需要进行这样的转化？
A：1. 简化优化问题。
在SLAM中常需对旋转矩阵进行优化，由于旋转矩阵具有正交性和行列式为 1 的约束，直接在李群上进行优化会引入额外的约束，使问题复杂。通过将问题转换到李代数上，可以将优化问题转化为无约束的优化问题，从而简化求解过程。
2. 局部线性化
以SO(3)和so(3)为例，李群SO(3)是一个非线性流形，其上的乘法操作是矩阵乘法，计算复杂度较高。而李代数so(3)是一个线性空间，其上的操作是向量加法和数乘。通过指数映射和对数映射，可以将李群上的乘法操作转化为李代数上的加法操作，从而简化计算。

至此，我们理解了为什么要有李代数这个东西，以及为什么要在实际问题中利用这个工具

3 - 李群李代数常用公式

（这部分的详细推导可见slam十四讲）

在 \(\mathbb{R}^3\) 中使用hat算子：

\[\omega^\wedge = \begin{bmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{bmatrix}^\wedge = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \in so(3). \]

类似地，我们可以使用vee算子将斜对称矩阵映射到 \(\mathbb{R}^3\) 中的向量：

\[S^\vee = \omega \quad \text{对于斜对称矩阵} \quad S = \omega^\wedge. \]

斜对称矩阵的一个有用性质是：

\[a^\wedge b = -b^\wedge a, \quad \forall a, b \in \mathbb{R}^3. \]

指数映射（在单位元处）exp : so(3) → SO(3) 将李代数的元素与旋转关联起来：

\[\exp(\phi^\wedge) = I + \frac{\sin(\|\phi\|)}{\|\phi\|} \phi^\wedge + \frac{1 - \cos(\|\phi\|)}{\|\phi\|^2} (\phi^\wedge)^2 \in SO(3). \]

指数映射的一阶近似是：

\[\exp(\phi^\wedge) \approx I + \phi^\wedge. \]

对数映射（在单位元处）将SO(3)中的矩阵R与斜对称矩阵关联起来：

\[\log(R) = \phi \cdot \frac{R - R^T}{2 \sin(\phi)} \quad \text{其中} \quad \phi = \cos^{-1} \left( \frac{\text{tr}(R) - 1}{2} \right). \]

\[\log(R)^\vee \in \mathbb{R}^3 \]

指数映射的增量近似：

\[\exp((\phi + \Delta\phi)^{\wedge}) \approx \exp((\phi)^{\wedge}) \exp((J_r(\phi) \Delta\phi)^{\wedge}). \\ \text{或者} \\ \approx \exp((J_l(\phi) \Delta\phi)^{\wedge})\exp((\phi)^{\wedge}). \]

其中 \(J_r(\phi)\) 是 ( SO(3) ) 的右雅可比矩阵，它将切空间中的加性增量与右侧应用的乘性增量关联起来（见图2）：

\[J_r(\phi) = I - \frac{1 - \cos(\|\phi\|)}{\|\phi\|^2} \phi^\wedge + \frac{\|\phi\| - \sin(\|\phi\|)}{\|\phi\|^3} (\phi^\wedge)^2. \]

\(J_r\)的含义：SO(3)关于so(3)的线性近似

\[\frac{\delta exp(\phi^\wedge)}{\delta\Delta \phi} \]

对数映射的增量近似：

\[\log(\exp(\phi^{\wedge}) \exp(\Delta\phi^{\wedge})) \approx \phi + J_r^{-1}(\phi) \Delta\phi. \]

噪声建模

资料：
符号定义来源 - IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation, Christian Forster∗, Luca Carlone†, Frank Dellaert†, and Davide Scaramuzza∗

公式推导来源 - https://ocw.mit.edu/courses/16-485-visual-navigation-for-autonomous-vehicles-vnav-fall-2020/d5d33eb19c2ed27d98ca66348133b3af_MIT16_485F20_lec16notes.pdf

位移的噪声模型

我们可以使用多元高斯分布来建模位移在 \(\mathbb{R}^3\) 中的不确定向量：

\[t \sim \mathcal{N}(\tilde{t}, \Sigma) = \frac{1}{\sqrt{(2\pi)^3 \det(\Sigma)}} \exp \left( -\frac{1}{2} (t - \tilde{t})^\top \Sigma^{-1} (t - \tilde{t}) \right) \]

其中 \(\tilde{t}\) 是分布的均值，$\Sigma \in \mathbb{R}^{3 \times 3} $ 是协方差矩阵。

定理（不确定向量的和）： 给定两个正态分布的向量 $t_1 \sim \mathcal{N}(\tilde{t}_1, \Sigma_1) $ 和 $ t_2 \sim \mathcal{N}(\tilde{t}_2, \Sigma_2) $，则有：

\[t_1 + t_2 \sim \mathcal{N}(\tilde{t}_1 + \tilde{t}_2, \Sigma_1 + \Sigma_2) \]

根据定理，对于固定的 $ \tilde{t} $，我们可以将 $ t \sim \mathcal{N}(\tilde{t}, \Sigma) $ 等效地写成：

\[t = \tilde{t} + \epsilon_t \quad \epsilon_t \sim \mathcal{N}(0, \Sigma) \]

旋转的噪声扰动模型

在 \(SO(3)\) 中定义不确定性的自然方法是在切空间中定义分布，然后通过指数映射将其映射到 \(SO(3)\)，其中 \(\epsilon\) 是三维向量，\(\Sigma\)是3x3的矩阵：

\[\tilde{R} = R \exp(\epsilon ^ {\wedge}), \quad \epsilon \sim \mathcal{N}(0, \Sigma), \]

\[\epsilon = \log(R^{-1} \tilde{R})^{\vee} \]

\(\tilde{R}\) 的分布为：

\[\tilde{R} \sim \mathcal{W}(R, \Sigma), \]

\(\mathcal{W}\) 指代这是一个扰动模型，其分布为

\[\mathcal{W}(R, \Sigma) = \frac{1}{J_R(\log(R^\top \tilde{R})^\vee)} \frac{1}{\sqrt{(2\pi)^3 \det(\Sigma)}} \exp\left( -\frac{1}{2} (\log(R^\top \tilde{R})^\vee)^\top \Sigma^{-1} (\log(R^\top \tilde{R})^\vee) \right). \]

当 \(\Sigma\) 很小的时候（即扰动 \(\epsilon\) 很小），则 \(\log(R^\top \tilde{R})^\vee\) 也很小（高概率情况下）。在这种情况下，\(J_R(\epsilon) \approx I_3\)，因此，分布可以进一步近似为：

\[\mathcal{W}(R, \Sigma) \approx \frac{1}{\sqrt{(2\pi)^3 \det(\Sigma)}} \exp\left( -\frac{1}{2} (\log(R^\top \tilde{R})^\vee)^\top \Sigma^{-1} (\log(R^\top \tilde{R})^\vee) \right). \]

附注：

1. 指数函数左侧的项也称归一化因子

2. 如何理解这个比例因子？（这部分是我的主观理解，证明可能有误）

   \[J_r = \frac{\delta exp(\phi^\wedge)}{\delta \Delta \phi} \]

   \(J_r \cdot \Delta\epsilon\) 意味着当 \(\epsilon\) 变化这么多（\(\Delta \epsilon\)）的时候，\(\tilde{R}\)的变化量。那么：

   \[\frac{1}{J_r \cdot \Delta\epsilon} = \frac{1}{J_r(\log(R^\top \tilde{R})^\vee)} = \frac{\delta \tilde{R} }{\delta \epsilon} \]

   于是这个因子可以被理解为从 \(so(3)\) 分布到 \(SO(3)\) 分布的缩放因子

3. 指数函数中的部分也有写作：

   \[{-\frac{1}{2} \left\| \operatorname{Log}(R^{-1} \tilde{R}) \right\|_\Sigma^2} \]

   它是一个用协方差矩阵加权的二范数，展开方式：

   \[\| \text{Log}(R^{-1} \tilde{R}) \|_{\Sigma}^2 = \left( \text{Log}(R^{-1} \tilde{R}) \right)^T \Sigma^{-1} \left( \text{Log}(R^{-1} \tilde{R}) \right) \]

4. \(\Sigma^{-1}\) 也称 Information Matrix 信息矩阵