相机模型复习

计算机视觉第一节课讲了点相机模型的内容，于是顺着笔记复习一下SLAM十四讲的第五章《相机与图像》

针孔相机模型

最基本的针孔相机模型由：一个物体、相机、物理成像平面组成

其中物体叫P，相机叫O，投影到P'，焦距是f，P(X,Y,Z)中Z是物像到相机的距离

由相似三角形，有\(\frac{Z}{f}=-\frac{X}{X'}=-\frac{Y}{Y'}\)，负号仅表示物像是倒置的

得到相机内参\((\frac{f}{Z}X,\frac{f}{Z}Y)\)，刻画的是物体坐标到成像平面坐标的转换参数

为了让公式看起来更通俗，可以把实际成像平面对称到物体一侧，得到对称成像平面，进一步还有归一化成像平面(Z=1)

相机捕捉到物体图像后，在成像平面上产生一个像素平面，物体在像素平面的坐标叫做(u,v)

从成像平面坐标到像素平面坐标存在一个转换关系：\(c_x，c_y\)的偏移量以及u轴缩放\(\alpha\)倍，v轴缩放\(\beta\)倍。方便起见将\(\alpha f\)记作\(f_x\)，\(\beta f\)记作\(f_y\)

偏移量描述的是相机捕捉图像时记录位置的偏移，缩放参数也叫量化系数，来源于制作CMOS时的倾斜

这些量也是相机内参，构成了K矩阵

\(K=\begin{bmatrix}f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1\end{bmatrix}\)

外参是相机的位姿R和T，对了，$\begin{bmatrix} R & T \\ 0^T & 1 \end{bmatrix}$称为位姿的变化矩阵

为了用矩阵运算的方式表达，还需要把P的坐标表示成归一化形式(X,Y,Z,1)
最后得到\(P_{uv}=\frac{1}{Z}K[R, T]P_{w}\)

自由度分析：K有5个自由度(包括距离Z)，Rotation和Translation各3个自由度，共11个自由度

由多张图像重建三维信息的方法

找到一个物理的点在多张图像中的位置，即一个P和很多个P'，一组位置便对应了一个方程，解方程组得到空间位置，还能得到相机的位姿(R,T)

难点在于找出一个特定的物理点在每一张图像中的像素位置（例如对于玻璃幕墙的大楼就很难做这件事，因而无法重建出三维的信息）

相机内外参的理解：内参矩阵用于从相机坐标系转换到像素坐标系，外参矩阵用于从世界坐标系转变到相机坐标系
两者都用上相当于把世界中的一个点对应到了成像平面上的一个像素

---

复习：方程组有解的前提
假设有一个包含 m 个方程和 n 个未知数的多元线性方程组，可以表示为 Ax = b，其中 A 为系数矩阵，x 为未知数向量，b 为常数向量

系数矩阵 A 的秩小于增广矩阵 [A | b] 的秩，方程组无解
系数矩阵 A 的秩等于增广矩阵 [A | b] 的秩，但小于未知数的个数 n，那么方程组有无穷多解

即便通过解方程恢复出了三维点的坐标信息，也未必就是实际的那个位置！可以说不能做到真正意义上的重建

---

再研究一下前两天相机矫正的配置文件ost.yaml

image_height: 480
camera_name: narrow_stereo
camera_matrix:
  rows: 3
  cols: 3
  data: [591.8388 ,   0.     , 307.4279 ,
           0.     , 591.18428, 203.97541,
           0.     ,   0.     ,   1.     ]
distortion_model: plumb_bob
distortion_coefficients:
  rows: 1
  cols: 5
  data: [-0.506324, 0.240337, 0.004244, -0.000858, 0.000000]
rectification_matrix:
  rows: 3
  cols: 3
  data: [1., 0., 0.,
         0., 1., 0.,
         0., 0., 1.]
projection_matrix:
  rows: 3
  cols: 4
  data: [487.76517,   0.     , 300.46796,   0.     ,
           0.     , 532.66229, 197.64988,   0.     ,
           0.     ,   0.     ,   1.     ,   0.     ]

  rows: 3
  cols: 3
  data: [1., 0., 0.,
         0., 1., 0.,
         0., 0., 1.]
projection_matrix:
  rows: 3
  cols: 4
  data: [487.76517,   0.     , 300.46796,   0.     ,
           0.     , 532.66229, 197.64988,   0.     ,
           0.     ,   0.     ,   1.     ,   0.     ]

可此相机内参是\(f_x=591.8388, f_y=591.18428, c_x=307.4279, c_y=203.97541\)
畸变系数是\([-0.506324, 0.240337, 0.004244, -0.000858, 0.000000]\)，前三个是径向畸变参数\(k_1,k_2,k_3\)，后两个是切向畸变参数\(p_1,p_2\)
修复畸变的公式是
\(\left\{ \begin{matrix} x_{distorted}=x(1+k_1 r^2+k_2 r^4+k_3 r^6+2p_1 xy+p_2(r^2 +2x^2)) \\ y_{distorted}=y(1+k_1 r^2+k_2 r^4+k_3 r^6)+p_1(r^2+2y^2)+2p_2 xy \end{matrix} \right.\)
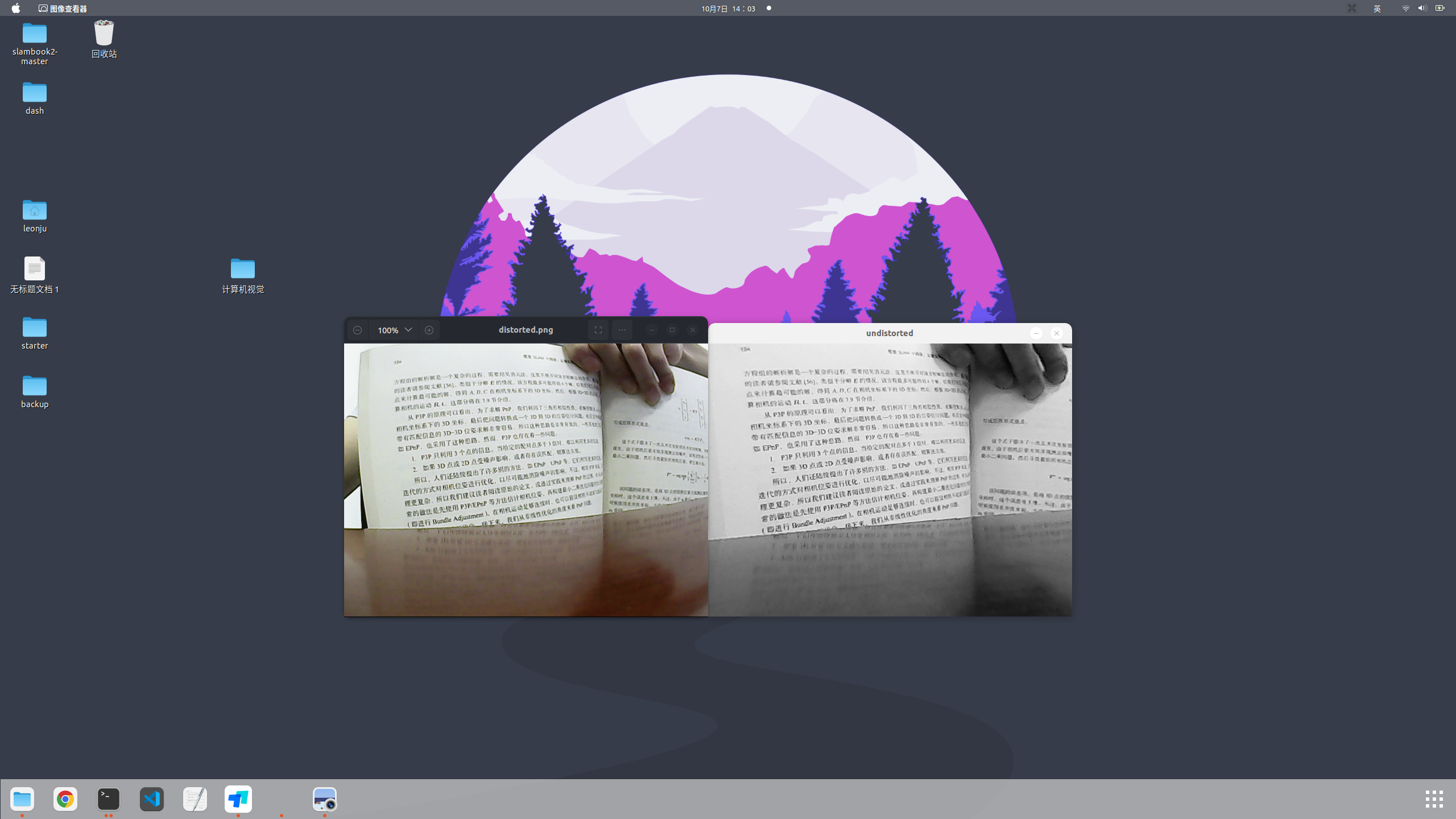
用SLAM十四讲第五章5.3.2节的图像去畸变方法，使用上面的参数调用opencv库去畸变得到效果如下：