P3 策略学习

Policy Function Approximation 策略函数

策略函数记做 π(a|s)

策略函数的输入是当前状态S 输出是一个概率分布，给每个动作一个概率值

如何得到这么一个策略函数，则需要构建一个策略神经网络，通过学习得到这么一个近似函数，还是以马里奥为例（包含左右上 三个动作，也就是三个维度）：

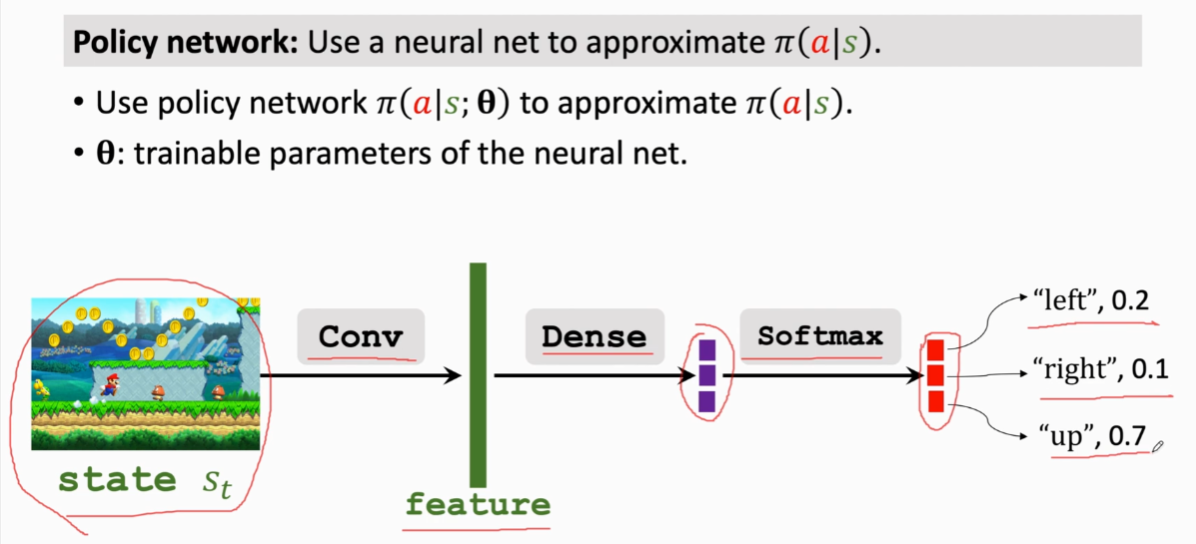
\[1.我们使用策略网络来近似得到策略函数，对于策略网络来说，\theta是神经网络的参数，开始\\是随机初始化的，后续通过学习来改进\theta 2.图中以马里奥为例，输入当前状态S，然后通过卷积层将状态变成特征向量，之后\\3.通过全连接层映射为3维向量，最后用softmax激活函数得到概率分布的三维向量\\ 4.概率函数的密度的性质我们知道相加和要为1 这里图中0.1+0.2+0.7=1 符合定义\\(这也是为什么要用softmax的原因，因为它可以让输出的是正数且和为1) \]

State—Value Function Approximation 状态价值函数

当状态是离散的时候，可以展开成π函数和Qπ的乘积形式（若是连续型的则是需要用积分来代替连加

Policy—Based Reinforcenment Learing 策略学习

主要思想：

V是来评价状态s的，对于输入的状态s，策略网络越好，V的值也就越高 。那么如何改进策略网络呢，我们可以改进模型参数θ，来让V(s;θ)变大。基于此想法，我们可以将目标函数设为θ的期望。

这是一个基于θ的目标函数，将状态S作为随机变量，然后对s求期望消掉s，这样只会剩下一个变量 θ

如何提高θ，则需要用到策略梯度的算法

β是学习因子，而后对于θ的求导则是策略梯度（policy gradient，即v函数对于神经网络参数θ的导数）

policy gradient

推导：

两种形式（等价的：

使用情况：

1. 若是离散型，如马里奥运动是 左、右、上的 则用第一种（本质上也就是每个离散值的累加 PS：不适用连续的

2. 若是连续型的，则用第二种，由于π函数是个神经网络，非常复杂，用普通的积分是求不出的，因此这里要使用蒙特卡洛近似来近似得到期望（PS:对于离散的也是适用的

   \[1.随机抽样得到动作\\ 2，3.用g(a,\theta)来近似表示当前动作的策略梯度（因为是其的无偏估计\\ \]

总结：

\[1.观察得到当前状态S_t\\ 2.随机抽样得到动作a_t\\ 3.计算价值函数Q_π的值，并记为q_t\\ 4.对策略网络π求导，得到策略网络π对于θ的导数d_{\theta,t}，其大小和θ是一样的\\ 5.近似的算策略梯度，用之前所提到的蒙特卡洛近似g(a_t,\theta)=q_t*d_{\theta,t}\\ 6.更新新的策略参数\theta_{t+1} \]

上述算法中还有一个没解决的问题，这个Qπ我们并不知道，因此算不出来这个值，因此我们需要近似计算这个值

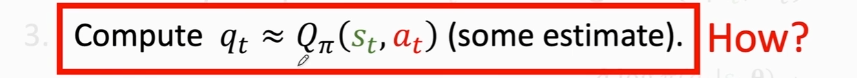
两个方法：

1. 

   \[1.完整的进行一局过程，记录每一次的状态，动作，奖励（s,a,r）\\ 2.使用上述公式得到u_t,u_t是所有奖励r的加权求和\\ 3.由于价值函数的Q_π是U_t的期望，因此我们可以用U_t的观测值u_t来近似Q_π\\ 4.我们用u_t来近似表示q_t\\ 总结：REINFORCE方法需要先执行一次，然后通过处理记录的数据来更新网络 \]

2. 

   \[使用另外一个神经网络来近似价值函数Q_π\\ 这也就是 演员—评论家方法 （具体见P4 \]

总结