由前序和中序序列重构二叉树
重构二叉树要根据需不需要 建树分成两种情况:
- 不建树:已知了前序和中序的序列时直接分割前,中序列就行
1 #include<iostream> 2 #include<cmath> 3 #include<string> 4 #include<cstdio> 5 using namespace std; 6 string a, b; //a前b中 7 void houxu(int x, int y, int p, int q) { //x~y为前序遍历 p~q为中序遍历 8 if (x > y || p > q) return;//规定边界条件 9 else { 10 int i = 0; 11 for (i = p; i <= q; i++) 12 { 13 if (a[x] == b[i]) break; 14 } 15 //int i = b.find(a[x]); //利用根左右的特性来在中序队列中查找 16 houxu(x + 1, x + i - p, p, i - 1); //递归左子树,因为前序先左再右,所以前序分割为左右子树两部分 17 houxu(x + i - p + 1, y, i + 1, q); //递归右子树 18 cout << a[x]; 19 }
20 } 21 int main() { 22 cin >> b >> a;//反一下输入 23 int l = a.length() - 1;//因为是0开始,所以要减一 24 houxu(0, l, 0, l);//递归 25 return 0; 26 }
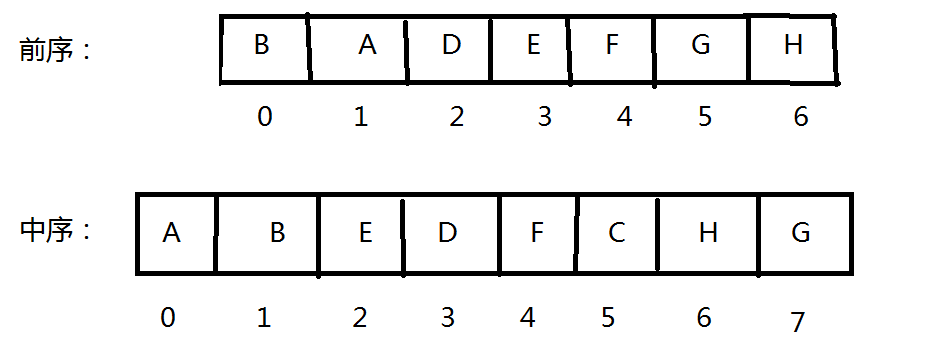
注意第16,17行的细节,C是根,前序中根后面紧跟着0~4为左孩子,个数为中序中确定共 i-p=5 个,所以递归左孩子时 传参x+ i-p,右孩子传参左孩子末尾的后一位 x+i-p+1
而中序中传参需要确定根的位置,循环在中序序列中找前序第一位元素的位置i,p~i-1是左孩子,i+1~q是右孩子
- 建树:需要在分割的同时构建T的结点和关系,最后得到一颗完整的树
1 void Recreatetree(TElemType* pr, TElemType* mid, int loc, BiTree& T) 2 { 3 if (loc == 0) 4 { 5 T = NULL; 6 return; 7 } 8 //赋值 9 T = (BiTNode*)malloc(sizeof(BiTNode)); 10 T->data.key = (*pr).key; 11 strcpy(T->data.others, (*pr).others); 12 // 13 int i = 0; 14 for (i = 0; i < loc; i++)//中序中定位 15 { 16 if (mid[i].key == (*pr).key) break; 17 } 18 //分割数组 19 Recreatetree(pr + 1, mid, i, T->lchild); 20 Recreatetree(pr + i + 1, mid + i + 1, loc - (i + 1), T->rchild); 21 }
因为传入前序 和 中序 序列的首地址后
- 给根赋值为前序的首位置对应的结点
- 找到中序中位置之后,前序首位值向后移一位,中序首位置不变,末位置即左孩子长度i ;并传入根的左孩子进行递归
- 找右孩子时,参照不建树类型,左孩子个数i-0个,所以右孩子序列的前序首位置应该后移i+1位,中序首位置后移i+1位,末位置即右孩子长度为总长loc-(i+1) ; 并传入根右孩子进行递归


