题解:B4400 [蓝桥杯青少年组国赛 2025] 第五题
闲话
板题,有一定码量和小细节(但是写起来很快,对称的复制粘贴即可),在这种只有 \(90\) 分钟的比赛中出这种题的组委会有点难评。
因此虽然思路简单,放个 T5 还是合适的。
题意
简要题意:有三个牛奶瓶 A、B、C,容积分别为 v,x,y 升,其中最开始 A 灌满了 v 升,B、C 没有牛奶。
每次操作可以任选两个瓶子倒牛奶:
- 如果可以倒满那就倒满。
- 否则全部倒入。
求是否可能让其中一个瓶子恰好有 \(\dfrac{v}{2}\) 升牛奶,如果可以输出最小操作次数,否则输出 -1。
做法
首先过掉一部分无解的情况,如果 \(A\) 是奇数那整数内部加减当然不可能有分数,因此是无解的。
鉴于数据范围很小,那当然是考虑搜索、枚举啦。稍微有些经验应该能看出来这是道经典的 BFS 入门练习题。
BFS 的做法是,我们维护一个状态队列,每次不断从队首得到新的状态然后将队首出队。如果队首已经有满足情况的就直接结束了,否则继续搜索。初始状态当然是 \(A\) 中有 \(v\) 升,\(B\) 和 \(C\) 没有,操作次数是 \(0\),可以用一个结构体维护。
接着,我们模拟题目中的倒牛奶过程,即 A 倒入 B、A 倒入 C、B 倒入 C,然后每种操作再分两类讨论。由于大差不差的,直接复制粘贴 3 组 \(6\) 条判断语句即可。操作完得到新的状态之后,将操作次数 +1 得到新的操作次数然后重新丢进队列里就算结束了。
但是这样子会超时的!考虑如下情况:
6 2 1
第一次,我们将 A 倒入 B,此时 A 还剩 \(4\) 升,\(B\) 有 \(2\) 升。
第二次,我们将 B 倒入 A,此时 A 有 \(6\) 升,B 空了。
哎这怎么又回去了?
我们发现我们需要存下来已经搜索过的状态,开一个三维数组记录即可(这也是为什么这题数据范围这么小,大一些开三维就 MLE 了)。
如果之前搜索过了就不用继续搜了(因为只会搜以前搜过的状态,反而步数更多了不优,某种意义上这也算是一个简单的最优性剪枝)。
最后,注意如果状态队列空了但是还没有结果那也是无解的,仍然返回 -1。
然后就结束啦!
DFS 也差不多,也可以做,也需要维护一个状态数组,只不过从队列改成递归搜索就好啦!
代码
赛场 ACCode:
:::success[代码]
图片版: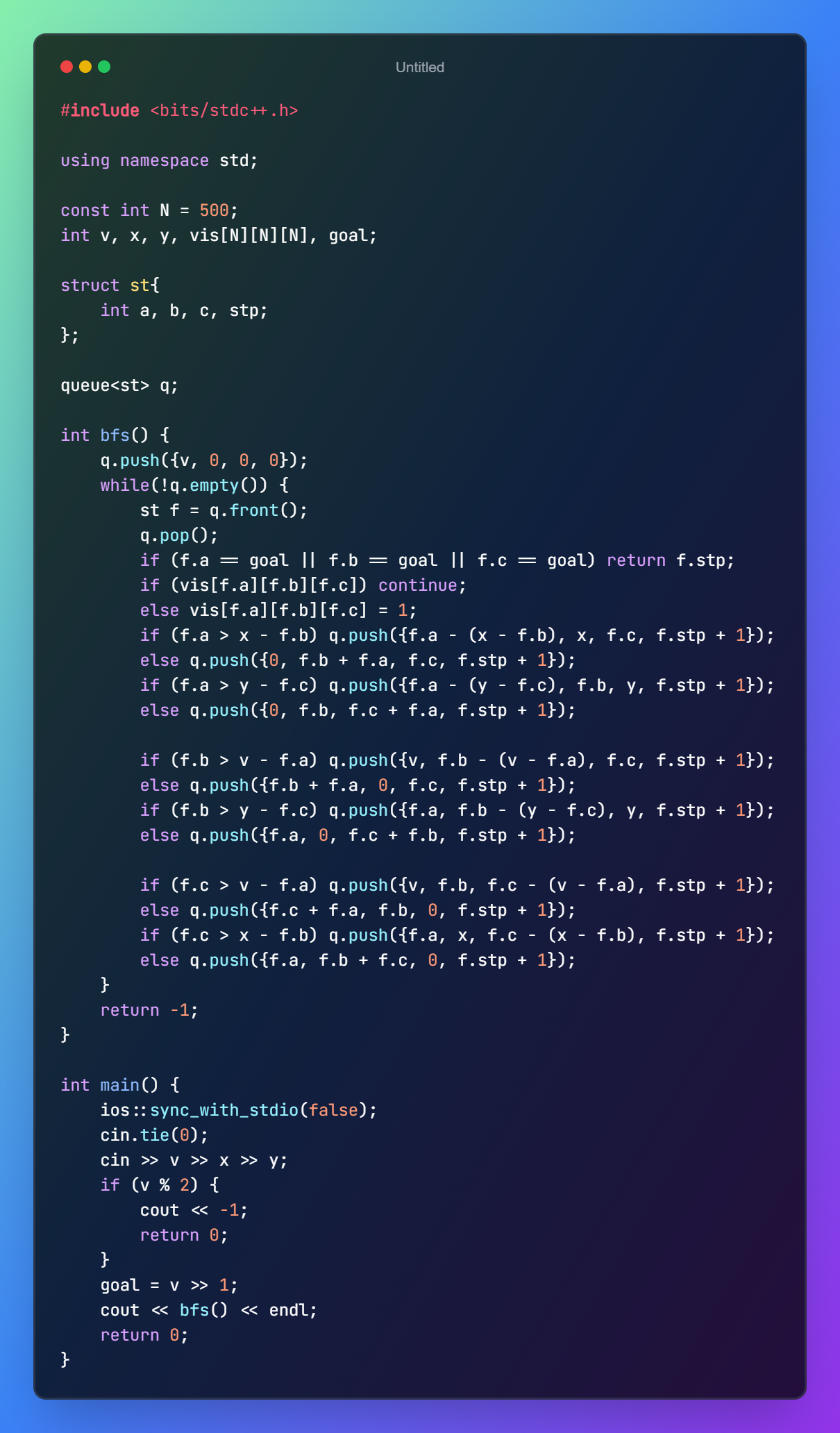
#include <bits/stdc++.h>
using namespace std;
const int N = 500;
int v, x, y, vis[N][N][N], goal;
struct st {
int a, b, c, stp;
};
queue<st> q;
int bfs() {
q.push({v, 0, 0, 0});
while (!q.empty()) {
st f = q.front();
q.pop();
if (f.a == goal || f.b == goal || f.c == goal) return f.stp;
if (vis[f.a][f.b][f.c]) continue;
else vis[f.a][f.b][f.c] = 1;
if (f.a > x - f.b) q.push({f.a - (x - f.b), x, f.c, f.stp + 1});
else q.push({0, f.b + f.a, f.c, f.stp + 1});
if (f.a > y - f.c) q.push({f.a - (y - f.c), f.b, y, f.stp + 1});
else q.push({0, f.b, f.c + f.a, f.stp + 1});
if (f.b > v - f.a) q.push({v, f.b - (v - f.a), f.c, f.stp + 1});
else q.push({f.b + f.a, 0, f.c, f.stp + 1});
if (f.b > y - f.c) q.push({f.a, f.b - (y - f.c), y, f.stp + 1});
else q.push({f.a, 0, f.c + f.b, f.stp + 1});
if (f.c > v - f.a) q.push({v, f.b, f.c - (v - f.a), f.stp + 1});
else q.push({f.c + f.a, f.b, 0, f.stp + 1});
if (f.c > x - f.b) q.push({f.a, x, f.c - (x - f.b), f.stp + 1});
else q.push({f.a, f.b + f.c, 0, f.stp + 1});
}
return -1;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); // 常数优化
cin >> v >> x >> y;
if (v % 2) { // 偶数 % 2 是 0,判断为 false,不会进入判断
cout << -1;
return 0;
}
goal = v >> 1; // 对于正整数,右移一位相当于除以 2
cout << bfs() << endl;
return 0;
}
如有除注释以外的差异以图片为准,文字版可以通过。
AC 记录:https://www.luogu.com.cn/record/233679115。
:::
DFS 的也有:
:::success[ACCode with 注释]
#include <bits/stdc++.h>
using namespace std;
const int N = 500;
int v, x, y, vis[N][N][N], ret = INT_MAX, goal; // ret 最开始要是一个极大值,否则怎么找都是 0
struct st {
int a, b, c, stp;
};
void dfs(int a, int b, int c, int stp) {
if (a == goal || b == goal || c == goal) {
ret = min(ret, stp); // 取最小值,dfs 不能保证第一次搜到的是最小的因此要记录一下,而 bfs 可以因此搜到了就可以直接返回结束了
return; // 不 return 就会继续搜下去然后就无限递归啦!
}
if (stp > vis[a][b][c]) return; // dfs 不能保证第一次搜到的就是最小的,因此只有步数大于已经搜过的步数时候才是更劣的
else vis[a][b][c] = stp; // 仍然记录步数
if (a > x - b) dfs(a - (x - b), x, c, stp + 1); // A 倒 B
else dfs(0, b + a, c, stp + 1);
if (a > y - c) dfs(a - (y - c), b, y, stp + 1); // A 倒 C
else dfs(0, b, c + a, stp + 1);
if (b > v - a) dfs(v, b - (v - a), c, stp + 1); // B 倒 A
else dfs(b + a, 0, c, stp + 1);
if (b > y - c) dfs(a, b - (y - c), y, stp + 1); // B 倒 C
else dfs(a, 0, c + b, stp + 1);
if (c > v - a) dfs(v, b, c - (v - a), stp + 1); // C 倒 A
else dfs(c + a, b, 0, stp + 1);
if (c > x - b) dfs(a, x, c - (x - b), stp + 1); // C 倒 B
else dfs(a, b + c, 0, stp + 1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
memset(vis, 0x3f, sizeof(vis)); // 初始化为一个极大值
cin >> v >> x >> y;
if (v % 2) {
cout << -1;
return 0;
}
goal = v >> 1;
dfs(v, 0, 0, 0);
cout << (ret == INT_MAX ? -1 : ret) << endl; // 不行就是 -1,注意判断 ret
return 0;
}
AC 记录:https://www.luogu.com.cn/record/233679675。
:::
完结撒花!
提示:这里情况比较多,空行区分和注释可以大幅减少 debug 的时间和代码阅读难度,相比于花大量的时间调不可读的代码甚至比赛结束也做不完,敲它们的时间是非常划算的。
推荐练习
P1135 奇怪的电梯。和这道题差不多,但是状态要少很多(因为只有向上和向下两种情况)因此要简单一丢丢。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号