散题练习：抱歉了我们是 焦点

UNR #8 D1T1

考虑这样一个事情：每次排序我们可以把一个小的值放到前面去，也可以把一个大的值放到后面去。但是我们发现，如果要把一个大的值放到 \(i\) 位之后，那么必须要有 \(i\) 个比它小的数在它后面给它垫背。而这说明在目标位及其之后必然有一个比它更小的。所以大胆猜测我们永远只会把小的值放到前面去。

所以容易导出一个做法。倒着扫，每次把一个最小的没用过的数挪到“酷的位”上，用一个小根堆即可。仔细分析一下在挪动区间包含的时候会有挪不过去的情况，但是显然可以调整一下让它们只交叉不包含。

CF1733D2 Zero-One (Hard Version)

dp 是可以的，但是我真的不想去想那个写挂两次的东西了。

来个很精妙的 \(\mathcal O(n)\) 做法。对很多题目都有启发性。

记 \(dif\) 为两个数组中不相同的位的数量。

显然，\(dif\) 为奇数是无解的。

首先考虑 \(y\leq x\) 怎么做。注意到这时候能和不相邻的换就和不相邻的换，所以只要 \(dif>2\) 就可以对折着来，答案是 \(\frac{dif\cdot y}{2}\)。特别地，对于 \(dif=2\) 且两个不同位挨在一起的情况，需要特判，答案是 \(\min(2y,x)\)（\(2y\) 源自于可以找一个其他点当中转）。

然后考虑 \(y>x\)。容易想到 dp，\(f_i\) 表示前 \(i\) 个差异被消灭的最小花费。考虑第 \(i\) 个差异的做法。当然可以把它和前面那个匹配在一起，这样转移：

\[f_i\gets f_{i-2}+(pos_i-pos_{i-1})\cdot x \]

或者进行半次 \(y\)。

\[f_i\gets f_{i-1}+\frac{y}{2} \]

看起来很神奇！考虑两个问题。

为什么不会出现半个 $y$？

考虑有解时必然有偶数个 $dif$，第一种转移消灭的 $dif$ 是偶数个，所以用第二种转移消灭的 $dif$ 也是偶数个。

进行半次 $y$ 时不用考虑相邻？

$y>x$，不合法不优。

感受一下就很对了，于是完成了一个难想但是十分自然的 \(\mathcal O(n)\) 做法。

trick：对于这种二元操作，可以考虑费用提前计算。

P8314 [COCI2021-2022#4] Parkovi

抽象题。

显然二分答案，然后转换成计算至少要多少个关键点才能覆盖掉整个树。覆盖的要求是到关键点的距离小于等于 \(mid\)。

我们考虑一个比较自然的想法：我们把树有根起来，然后考虑自下而上的一个过程。这样我们容易想到在必须要放的时候才放一个关键点干掉子树里面没被管到的点。

通过链部分分也能想到这个。

显然在最优解中，任何一个关键点往更深的地方走都是不优的，所以这样做确实非常有道理。并且我们不关心根选什么，因为最优方案并不关心树是什么形态的。

问题是怎么写。首先肯定是一边 DFS 一边贪。很明显 DFS 路途中我们需要确定一个点 \(x\) 是不是必须要放的点，具体来说，是不是 \(x\) 子树内有些没被管到的点，如果 \(x\) 不是关键点，那关键点再往父亲挪就管不到了。那么我们只需要考虑离 \(x\) 距离最远的没被管的点就行了。

这里我们可以考虑每一个儿子子树中最远的没被管的点并继承过来，然后考虑它会不会被别的子树里的关键点管到（很明显这里只需要考虑别的子树中到这里的最近关键点距离），如果不会，则它对 \(x\) 是不是关键点有决策作用，做贡献。

最后看一下最远的那个没被管的点到 \(x\) 的距离和到 \(x\) 父亲的距离来 check 一下 \(x\) 关不关键就完事了。

P8162 [JOI 2022 Final] 让我们赢得选举 (Let's Win the Election)

终于会了这题，比一年前的我强。一时间感慨万千。

下文的 \(A,B\) 指代对每一项的选择。

显然，看完题就会有一些我们一眼秒的性质：

• 确定 \(B\) 的选法后一定从小到大选
• 剩下的 \(A\) 一定在剩下的部分从小到大选
• 一定先做 \(B\) 再做 \(A\)

那么我们容易得出一个按照 \(B\) 从小到大选择的贪心，可这是错的。你考虑你选了一个小一些的 \(B\)，但是损失了一个极小的 \(A\)，我们可以用一个略大的 \(B\) 换取这个极小的 \(A\) 自由，那么可能会更优秀。

选择方法有这么多性质，怎么做呢？

我会刻画答案形态！

按照 \(B\) 排序之后，我们选出一个 \(B\) 的 \(len\) 长子序列顺序操作 然后在剩下的部分顺序选择 \(k-len\) 个 \(A\)。我们发现，\(B\) 的最后一项之前是一定没有不取的项的，不然可以把最后一个拿过去更优秀（反正 \(A\) 也不选它）。

所以 \(B\) 的最后一项之前一定是填充满了的。如果前面还不够票数，需要再在后面选择最小的几个 \(A\)。

这个填充满了的性质很漂亮，可以帮助我们 dp，后面的部分可以贪心选择。具体来说，枚举 \(len\)，\(dp_{i,j}\) 表示前 \(i\) 个数里面有 \(j\) 个选择 \(B\) 的前半部分最小答案，那剩下的 \(i-j\) 个都是 \(A\)。转移比较显然。右边还有 \(k-i\) 个最小的数是 \(A\)，容易合并在一起。这两者合并就是这一种情况对状态的贡献。

最后直接输出最小贡献即可。

非常棒的刻画答案形态题。答案性质很多就考虑仔细刻画！刻画完之后一般容易用一个 dp 来表示或者直接贪心。

代码：https://atcoder.jp/contests/joi2022ho/submissions/56386223

P3589 [POI2015] KUR

你考虑 \(c\) 串中的一个匹配串，那么它从头开始的连续 \(m\) 位 \((ai+b)\bmod n\) 和 \(p\) 的关系都确定了。很自然想到把“头” \(s\) 分离出来得到每一位 \(i'\in[0,m)\) 的 \([a(i'+s)+b]\bmod n\) 和 \(p\) 的关系都确定了。

此时我们容易想到，“头”的个数其实就是出现次数，而且 \(i'\) 是可一位一位枚举确定的，所以我们分离常数：

\[\begin{aligned} &[a(i'+s)+b]\equiv x\pmod n\\ &\iff as+ai'+b\equiv x\pmod n \end{aligned} \]

因为 \(a\perp n\) 并且 \(s<n\)，所以对于任意 \(as\bmod n\) 的值我们一定可以通过逆元解出唯一对应的 \(s\)。换句话说，我们想数“头”\(s\) 的数量可以改成数有多少个合法的 \(as\)，只不过要去掉不符合要求的 \(s\in[n-m+1,n)\)。

因为我们知道 \(x\) 和 \(p\) 的大小要求，所以我们也可以得出 \(as+ai'+b\) 和 \(p\) 的大小要求。因为 \(i'\) 可枚举，所以 \(ai'+b\) 事实上是常数，那么我们也能分离出 \(as\) 的大小区间（因为 \(\bmod n\) 是环状区间所以可能有两端）。

对所有 \(i'\) 分离出的 \(as\) 大小区间使用离散化差分或直接在 set 中差分求区间交即可。

当然还要取出不合法的 \(s\)。我们可以提前预处理所有的不合法 \(as\)，所以排序之后 lower_bound 去除一下就行。

P9520 [JOISC2022] 监狱

tricky 题。

我们考虑不合法的路径集怎么判断，你画一下发现不是很好做。所以我们考虑怎么判定合法路径集。

直接弄一头雾水，考虑刻画合法路径集的行走方式。

你考虑把每条路径单独拿出来看，那么它一定是“每次在最短路径上走一步”的原走法的子序列，那么容易想到刻画该子序列相邻两项之间的情况，这里拉一张原题解的图：

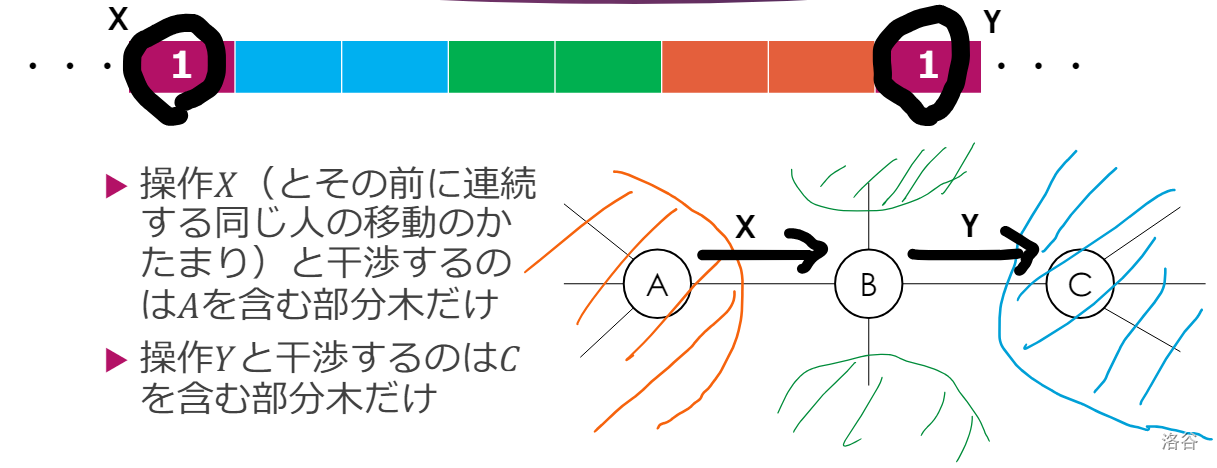
考虑 \(X\) 是 \(A\to B\) 行走，\(Y\) 是 \(B\to C\) 行走，它们是一条路径的行走子序列中的相邻两项。

显然，在 \(X\) 之前 \(B\) 这里不能有挡路的。

两项中间的行动有三类：绿色区域内的移动、橙色区域内的移动、蓝色区域内的移动。我们显然可以重排使得：进行蓝色、\(A\to B\to C\)、进行橙色绿色。这样我们就把不连续的行动变成连续的了。

容易发现，走到 \(C\) 之后，这边的“橙色绿色”会是下一步的橙色，所以合并过去，就能造出一条连续的合法走法。容易发现子序列之间是独立的，所以最终方案一定是一个一个连续走完。

感性理解是：如果有人走到半路要停下来等别人走，那也可以让那个人先走完或者自己先走。

画一画也能观察到这个。

那唯一的阻碍就是有些路径必须比一些先走（因为走过去不能有挡路的），也就是起点在其他路径上的必须比其他路径先走，终点在其他路径上的必须比其他路径晚走。有环显然就无解了。

树剖后线段树优化建图，拓扑排序即可。

没那么即可。我们发现我们要做的是一个点向路径上的一堆有效点连边，或者路径上的一堆有效点向一个点连边，怎么确保只连接有效点呢？我们考虑只让有效点有效。

我们要在原树上弄树点方便连边，还要一堆路径点来表示路径之间的拓扑序关系。

具体来说考虑所有路径 \((u_i,v_i)\)：

• 在上行树（起点树）上，这一条路径上的所有树点向路径点 \(i\) 连边，表示这些树点背后可能含有的起点要先于 \(i\) 行动。
• 在下行树（终点树）上，这一条路径上的所有树点被路径点 \(i\) 连边，表示这些树点背后可能含有的终点要后于 \(i\) 行动。

为了联络树点和路径点，把“背后”这个东西在合理的时间复杂度内体现出来，而又不影响无关的点，根据起点要先于、终点要后于的拓扑序，我们显然要从路径点连到树上起点，再从树上终点连到路径点。这样做后可以发现，去掉无用的树点后其实就相当于直接用路径点的关系连边，但是每条边上插了一个树上起点或树上终点搭桥方便优化。

比较有意思的题。

CF279E Beautiful Decomposition

好题。

首先我们可以发现每个 \(2^k\) 最多用一次。

然后我们容易想到一个 dp：我们从高位往低位，让高位全部弄好（因为低位也干涉不了高位），记录现在更低位是需要加还是需要扣。可以发现，需要加就是要直接加出后面的位就行，需要扣则需要把后面的位全部反过来然后看成是加法。

那么我们设计状态 \(f_{i,0/1}\) 表示目前处理到第 \(i\) 位，后面的位要加还是要扣的最小值。你可以把扣看成是加出来它的补码，初值设置为 \(1\)（因为一开始为了变反还需要一步），然后应该就可以了。

没怎么细想，之后可能需要回来看。

CF2006C Eri and Expanded Sets

简单题啊。。。

考虑合法状态一定是无法操作的，那么考虑无法操作的充分必要条件，显然是整个集合构成一个等差数列且公差为奇数（任意两个相邻元素差不能是偶数，且差必须相等）。

那么你发现你的要求就是最终相邻两个数差分的绝对值的 \(\gcd\) 是 \(1\)，这显然等价于任意两个数差的绝对值的 \(\gcd\) 是 \(1\)。在这个题里面，我们能做的只有把两个数的差除以 \(2\) 放回去继续 \(\gcd\)，所以我们猜测只有原 \(\gcd\) 是 \(2\) 的幂次才是一个合法方案（其他质因数是消除不掉的），事实也的确如此。

接下来我们发现所有数的差的 \(\gcd\) 其实就是排序后两两相邻差的 \(\gcd\)，这容易用辗转相除证明。

其实不用排序，这也容易用辗转相除证明。

发现固定端点后这个东西显然是单调的一段后缀可行，双指针加线段树即可。

P10371 「LAOI-4」石头

想出来了写不出来。。

你考虑刻画什么样的端点是可行的。你发现，\(i,j\) 之间的最大值 \(mx\) 是一个必须要跨过的门槛，那么为了跨过它，所有 \(i\) 左侧的小于 \(mx\) 的数都会被染色，\(j\) 右侧的小于 \(mx\) 的数都会被染色。由于中间被染色的数量总是 \(j-i+1\)，我们就比较这两段就行了。这种贡献我们容易通过直接枚举最大值位置，看左右两侧第一个比自己大的数的位置来确定。

问题是最大值 \(mx\) 可能是其中一个端点，此时门槛就变成了次大值 \(cm\)。我们仍然枚举次大值，然后不妨假设最大值位于 \(i\) 侧。对于 \(i\) 的部分，因为 \(mx\) 自然染好所以只需要跨越 \(cm\)，那么所有 \(i\) 左侧的小于 \(cm\) 的数都会被染色，而 \(j\) 的部分仍然需要跨过 \(mx\)，所以 \(j\) 右侧的小于 \(mx\) 的数都会被染色，我们尝试让这两个东西相等。

\(i\) 左侧小于 \(cm\) 的数的个数容易通过计算 \(cm\) 左边第一个、第二个比它大的数来确定，因为显然如果最大值在 \(i\)，那么 \(cm\) 左侧第一个比它大的数就是 \(i\) 这个位置。\(j\) 向右染色的右界显然是 \(mx\) 右边第一个比它大的数，所以我们可以根据两侧相等算出 \(j\) 的位置，然后判定 \(j\) 是否没有达到 \(cm\) 右边第一个比它大的数（因为达到了 \(cm\) 就不再是次大值了）。

画图之后特别好理解。场上没有想清楚原理。

tsx Round 1 树状数组（fenwick）

好难……

你容易翻译两种操作形如：

• 1 操作：一整个区间的树状数组对应节点所表示的区间加。
• 2 操作：区间求和。

注意我们容易把它刻画成在树状数组上的操作，但是我们不要这样做。我们把树状数组和数组拆开。

1 操作本质是区间套区间，你先考虑单点修改，那么就是个纯粹的区间加，这个玩意形如在树状数组的一个节点上打上懒标记，这个标记我们要下推给它管理的所有树状数组节点，本质是要推给数组上它管理的所有位置。

怎么推？用线段树来推！

把 \(n\) 扩展到 \(2^k\)，那么树状数组的每一个节点对应的区间都对应线段树上一个节点。我们想做的这件事情就是在这个节点上打一个区间加标记，在线段树上查询的时候线段树会帮我们推的。

现在换成区间加。那么我们本质上是要给一个区间的树状数组节点都打上区间加懒标记。那么我们直接进行套娃，我们打一个懒标记的懒标记，当推到树状数组节点的时候我们就把它挪到区间加标记上，然后正常推区间加标记即可。

写的时候需要注意不能直接给 \([l,r]\) 做 modify，因为我们考虑的树状数组节点是所有右端点在 \([l,r]\) 的节点，左端点不确定。所以要做一次 \([1,r]\) 再做一次 \([1,l)\) 来容斥。

pushdown 的时候需要注意“懒标记的懒标记”对和的影响，这个东西在数组上的贡献应该是区间内所有树状数组节点状区间，所以预处理这玩意的长度和来 pushdown 即可。

时间复杂度 \(\mathcal O(n\log n)\)，有一个树状数组写法，但是需要很先进的树状数组理解，交给 SA 好了。

tsx Round 1 括号序列 (bracket)

先考虑一个暴力做法：经典地，我们维护左括号栈，考虑每次进来的右括号想要拿到自己的左括号，就必须和中间还没走的左括号对立。那么我们就可以连边，然后跑二分图染色。

形式化地，所有 \(l_1<l_2<r_1<r_2\) 的 \(1,2\) 之间进行连边。

正确性显然。

现在我们考虑优化。

注意到，所有连通块都是不相交的。事实上这是容易证明的，只要刻画一下 \(l_1<l_2<r_1<r_2\) 情况下 \(l_3,r_3\) 的位置就会发现 \(l_3,r_3\) 要么不交要么连通。鉴于括号匹配可以拉得很长跨过一整个连通块去连通，所以可以存在包含。

我们继承第一个想法。经典地，我们从左向右扫括号序列，但是维护一个连通块栈。显然这些连通块中都必须包含未被匹配好的左括号，否则已经完备可以弹出不影响。

扫到左括号时，它暂时单独成为一个新连通块。扫到右括号时，我们考虑它的左括号所在的连通块。

首先中间所有的连通块因为都有没匹配的左括号所以要连通在一起。然后我们考虑染色。中间这些连通块中因为必须保留未匹配的左括号（不能和这个右括号匹配），所以在弹出的连通块的并中不能两种颜色的未匹配左括号都存在，如果存在就是无解。否则就是都存在一边，那么这个括号必须和那边的所有括号颜色相对，这个限制我们先不考虑怎么在图上表示。

我们考虑合并连通块怎么完成。现在我们已经弹到了这个右括号的对应左括号的连通块。首先这个左括号必须是这个连通块某种颜色的最右端未匹配左括号，否则中间还有其他括号，那样无解。如果可以，那么删掉那个左括号，然后把后面的一堆连通块合并。合并时我们需要把所有未匹配左括号全部扔到对面的颜色里面去，同时又需要保证每次删掉顶上的括号之后下一个括号是最靠右的，那么我们尝试使用链表。

用链表维护连通块中两种颜色的未匹配左括号，且按照从前到后从左到右的顺序连接。可以发现，无论连通块形态如何（被包含的连通块或是不相交的连通块），所有连通块中的未匹配左括号一定是整体按顺序排好的。换句话说，我们想在合并的时候连接链表，直接首尾相连就能保证未匹配左括号顺序正确。

证明可以考虑，不相交的肯定是对的，如果出现被包含，可以发现，那么一定是存在跨过整个本身连接的未匹配左括号或者是一个跨过去匹配的右括号，这两者都必然是右括号进来合并的结果，那么不可能不合并这个连通块，所以矛盾了。这也侧面证明了在我们这种维护方式下这个栈里面的所有连通块都是不相交且不包含的。

现在都说得通了。现在我们考虑怎么表示某个括号必须和某一边的所有括号颜色相对。首先一个很容易理解的做法是我们随便连一个左括号就行了（最简单的办法是连头头的那个括号），因为那些括号早已经被钦定颜色相同。这个做法的本质是，其实现在我们已经确定了一个合法方案（显然是的，同色的在一个链表里面，不同色的在另一个链表里面），但是我们需要染一遍色来保留方案（因为链表里面不会留下所有项），所以我们只需要把不同色的连成一个树形结构来进行最终染色就行。

可以发现每合并一次连通块就会加至多一条边，且每条边的一个端点都是新括号，所以最后一定会产生一个森林，这就是合法方案的一个生成森林，直接跑染色即可。

CF513D1 Constrained Tree

神级 *2600 构造题。想了半天端出来一坨史。唉，没想清楚啊。

首先我们容易想到把限制挂到根上然后递归构造，然后我们会发现每个点上的限制其本质是要求左右儿子用的点在一个区间里面。这个区间首先受到先序遍历的制约（左儿子为这个点 \(+1\)，右儿子为左儿子最大值 \(+1\)），其次受到输入的子树限制制约。

通过制约一可以发现，左儿子的编号永远是确定的。所以我们考虑先递归构造左儿子。同时因为右儿子受到制约二，所以我们希望左儿子在构造时尽可能不多占用点。

我们维护 \(x\) 表示目前在构造 \(x\) 子树。那么先考虑左子树，左子树在这个点上挂有若干制约，其中要求了一些点必须被构造在左子树里面。因为左子树必然是一个区间，那么这些制约的最大值往前都一定会被构造进去。所以我们同时 \(lim\) 表示这个子树至少要构造到编号为 \(lim\) 的点，要求这个子树必须构造到点 \(lim\)。

制约不会传递吗？只考虑这个点上挂的制约会不会错误构造？

制约会传递，但是能传递到这个点上的制约总会在往子树递归构造时被考虑到。注意 $lim$ 表示的是至少要构造到哪个点。

这样就做完了。判无解是容易考虑的。

CF354B Game with Strings

咕一下，\(\min-\max\) 对抗原来可以正推吗。

CF1499F Diameter Cuts

很厉害的设计状态题，容易想到子树合并型 dp。也不知道为啥我这么笨。

我们很想把直径塞进状态里面，但是我们发现怎么都不行。那么另一个呼之欲出的想法就顺理成章上位了：\(f_{i,j}\) 表示以 \(i\) 为根的子树内从根下去最长的链长度为 \(j\)，并且满足条件的方案数。

我们考虑在子树合并转移的时候保证这个条件。

首先考虑这条边断开，那么没有什么影响，对于所有 \(j\) 我们都更新 \(tmp_{u,i}\gets dp_{u,i}\times dp_{v,j}\)。注意这里必须拿另一个数组来帮忙转移，因为我们要用原数组的答案又要更新原数组。

考虑这条边不断开，那么显然我们要求 \(i+j+1\le K\)，才能使得根连通块的直径不到 \(K\)。那么转移 \(tmp_{u,\max(i,j+1)}\gets dp_{u,i}\times dp_{v,j}\) 即可。

然后就做完了。整个东西形如一个树形背包，直接写就是 \(\mathcal O(n^2)\) 的。

CF1630D Flipping Range

首先想到两次操作可以发生改变 \(a_i,a_{i+k}\) 正负性的这么一个操作，那么继续下去可以改变 \(a_i,a_{i+xk}\) 正负性。

然后发现这个 \(B\) 就是搞笑的，有用的只有它们的 \(\gcd\)，假设就是 \(k\)。

这样只剩一个数了。那么你可以按照顺理成章想到按照 \(\bmod k\) 剩余系分类，那么每个剩余系的贡献容易通过讨论负数个数奇偶性取得（因为每次操作可以去掉任意 \(0/2\) 个负数），而我们发现这是符号无关的，每个剩余系都贡献自己里面绝对值最小的数。也就是说，我们现在已经不关心数了，我们的最终答案只由每个剩余系的负数个数奇偶性决定。

但是没完。你发现还可以有一些散装操作。每一个操作恰好覆盖到每个剩余系里面的一个数，所以会改变每个剩余系的负数个数奇偶性。所以把每个剩余系的负数个数奇偶性正过来倒过来各做一次即可。

做题的时候没有想到那个符号无关的观察，导致后面一直被散装操作卡瓶颈了。

CF417E Square Table

逆天构造题。

首先你发现行列独立。为什么？因为你任何一个 \(n=1,m=1\) 的方案可以合在一起。

我们发现任何一个方案整体乘一个常数是不影响方案是方案的。如果我们现在有一个 \(n=1\) 的方案 \(\{a_n\}\) 和一个 \(m=1\) 的方案 \(\{b_m\}\)，那么我们在最终答案里面 \(M_{ij}=a_i\times b_j\) 就很合理。每一列上都是 \(M_{i1}\) 方案的一个扩倍（扩 \(a_j\) 倍），每一行上都是 \(M_{1i}\) 方案的一个扩倍（扩 \(b_j\) 倍），所以就合法了。

然后我们考虑怎么做 \(n=1,m=1\)。我们考虑一个比较套路的思考：放一堆一样的数，只改几个数。然后我们打表或者观察构造发现，对于偶数可以先放一堆 \(1\) 然后放 \(\frac{n-2}{2}\) 就可以，对于奇数先放一堆 \(2\) 然后放 \(n-2\) 就可以。然后就做完了。

CF1237E Balanced Binary Search Trees

一道很幽默的题。

我手玩了 \([1,14]\)，发现只有 \(1,2,4,5,9,10\) 是有解的。

手玩途中发现，\(9\) 是左边一个 \(n=4\) 右边一个 \(n=4\) 拼起来的，\(10\) 是左边一个 \(n=5\) 右边一个 \(n=4\) 拼起来的。这很好理解，根据 BST 性质，总是可以按照根的值划分出两个区间给子树，所以新树应该是由一个合法左子树和一个根为偶数的合法右子树拼起来的。

然后我们发现这个 Balanced 的条件很强，\(4,5\) 必须用 \(1,2\) 拼起来，\(9,10\) 必须用 \(4,5\) 拼起来，下一层必须用 \(9,10\) 拼起来，否则就会有层空缺。于是事情就很简单了，我们直接往后面递推，看一下根的奇偶性拼一下就行。答案就是 \(0\) 或 \(1\)。

CF1819C The Fox and the Complete Tree Traversal

首先容易发现，找出直径之后不存在挂着深度大于 \(1\) 的树（也就是一条长度大于 \(1\) 的链），否则无解。

容易通过讨论从哪个点跳上这条链证明是无法同时能够过去回来的（因为必须要构成一个环），也容易感受，这里不细讲了。

主要说说怎么构造方案。

一个比较精妙的想法是你发现黑白染色就是对的，先一条线过去把黑点走完，一条线回来把白点走完就行。显然任意两个黑点或白点到最近的同类点的距离都不超过 \(2\)，两边也衔接得起来，最重要的是黑白点的分布很有规律，直接一条直径扫过去就可以了，非常好写。

有点脑电波的题。

LPH Cup T2 破

本题灵感点：一个对观察的重新上树的思考维度转化。

其实是比较简单的题。

首先容易猜测每次答案一定是继承过去的。其实这也容易用 Exchange Argument 证明，有 \(+2\) 不用用一次 \(+1\) 是不优的。

然后容易有一个观察（无论是看大样例还是感受）：这个答案应该是形如一堆 \(+1\) 和一堆 \(+2\) 构成的。然后你马上就能证明答案至少增加 \(1\) 至多增加 \(2\)。

手画一下可以发现这个的原理：我们一开始选了一个叶子之后我们可以选择一些点和它一起点 LCA，这样就会产生 \(+2\) 的贡献。但是有的时候我们点不了了就要另开一个叶子接着点。

这样我们会有些贪心的想法，现在没有得到证实的，所以不讲。

我们考虑答案形态形如一堆 \(+1,+2,+2,+2,+2,\cdots\)，我们把这样的分成一段，考虑这一段在树上的形态。我们发现，每个被使用的 LCA 最多实现一次 \(+2\)，所以我们可以直接把这种 LCA 归进它 \(+2\) 的那一段里面，这样每一段在树上就是一堆 \(+2\) 的 LCA 和一堆叶子，其中恰好有一个是 \(+1\)。然后对于同一段在树上用虚树的方式连起来，你发现刚好连成连通块并且非常刚好：

• 首先，除了二度点可以不属于任何一段以外，其他点都会被当做 LCA 使用，也就刚好会成为一个划分。
• 其次，任意一个连通块里的点都是至多二叉的，因为一个点有三叉，那么第三个子树里面第一个被选的点就是 \(+1\)。
• 连通块里面深度最小的点是一个被使用的 LCA。

此时思路就比较明了了，我们要在树上划分一些这样的连通块，让连通块的大小之和最大，就是答案。由于是划分而且每个连通块都有一个深度最小点的特征，所以子树之间是独立的，我们可以一个子树一个子树从下向上划分统计连通块，每次把儿子连通块往根合并就可以了。

我们考虑 \(f_i\) 表示 \(i\) 为最小深度点的这种连通块最大能有多大。然后我们考虑从下往上 dfs，然后合并在一起：

• 一度点 / 二度点无所谓。一度点连通块大小是 \(1\)（叶子嘛），二度点继承上去，删掉儿子连通块。
• 多度点因为连通块每个点最多二叉，所以可以合并两个儿子的连通块，你发现很 amazing，其中后一个儿子的连通块里面的 \(+1\) 可以被这个根点成 \(+2\)，所以直接加在一起合并上来就行。因为我们最后需要一个划分，所以这两个儿子的连通块不再存在。

然后你贪心地发现我们取最大的两个连通块合并上来是很行的。

最后我们就能得到一堆连通块的划分，全部从大到小排序还原回去就行。

妈的，怎么这题这么难表达做法，但是感受起来特别容易。

LPH Cup T3 Q

本题灵感点：一个从贪心方法得出的 dp，还有一个比较 tricky 的斐波那契分治。

一眼可以秒掉，这个东西先子序列再子串，其实就等价于在串里面找一个位置开始子序列匹配，那么从这个位置开始的最小子串长度就是最后一个匹配位置和这个位置的距离差，这是比较显然的。

这样我们能直接得到一个 \(\mathcal O(S^2)\) 做法，但是没啥 p 用。

数学直觉告诉我们答案串不可能是 \(S_{\infty}\)，肯定不会太长。事实上确实如此。观察发现这个串的性质就是每三个字符有一个 \(\texttt{a}\) 或者 \(\texttt{b}\)，所以 \(3n\) 的长度就肯定可以贡献一个答案。暂不清楚题解如何证明在 \(3n\) 的界内能找到最短答案（主要是可以拼接串），但是题解宣称在 \(|S_{30}|\approx 8\times 10^5\) 内可以找到最短答案。

那么现在我们可以枚举从哪个串匹配到答案，但仍然不能直接 \(\mathcal O(n^2)\)。

此时肯定要利用串是斐波那契的性质。你考虑这个字符串的子序列匹配在它的最短被匹配串 \(S_i\) 里面长成什么样：肯定是一段前缀在 \(S_{i-1}\) 里面，剩下的一段后缀在 \(S_{i-2}\) 里面。

于是你容易想到一种办法怎么判定一个区间合不合适：进行一个分治。把 \(S_{i-1}\) 的拿给 \(S_{i-1}\)，把 \(S_{i-2}\) 的拿给 \(S_{i-2}\)。如果区间不完整就继续划分下去，这样我们就会像线段树一样把整个区间划分开，每个划分出来的段都恰好是一个 \(S_{x}\)。由于斐波拉契性质，每一次拆都会把区间长度除以 \(2\)，所以我们最后只有 \(\log\) 层，而每一层除了最底层至多贡献一个串，所以划分只有 \(\log\) 个串。于是我们试图合并这些区间，看能不能合并出来一个完整的匹配。

直接暴力扫肯定不合适，此时容易想到考虑弄一个 dp 合并，因为整个东西长成一段一段拼起来的，每一段都有一个子序列匹配的贪心，我们沿用它：\(f_{i,j}\) 表示在串 \(j\) 中从 \(i\) 开始最远能贪心匹配到哪之前，那么转移显然就是：

\[f_{i,j}\gets f_{i,j-1}+f_{i+f_{i,j-1},j-2} \]

比较显然！

这样我们就能在 \(\mathcal O(\log n)\) 的时间复杂度用一个线段树状物判定了。

然后你回到我们原来的问题。我们是要找一个最小的区间满足把这个区间扣下来可以匹配完整个串。首先我们枚举 \(S_{30}\) 里面所有串的所有位置当做左端点，然后考虑右端点。可以发现单调性，右端点随着左端点向右移动肯定向右，直接上双指针用判定即可。因为左端点级别是 \(\mathcal O(n\log n)\) 的所以整个东西复杂度是 \(\mathcal O(n\log^2n)\)。由于 \(\log\) 来自数量级，所以没有常数，跑得很快，好像 \(\mathcal O(n\log^3n)\) 都过了。

SA Cup T2 门铃的余音

很好的题。

首先你要读对题，你可以积蓄很多次能量然后狂按门铃。

那么这样你会有一个显然的想法，就是一开始就一直在按照某个 \(b\) 的顺序不断积蓄能量，剩下的按就是了。这样每个 \(b_i\) 所对应得到的按铃就投入在一个后缀里的任何一个点。我们可以看成对 \(b\) 垒前缀和之后放了一堆点，每个点都可以往后移动。

这样会有另一个显然的想法，就是把积蓄需要的时间按照从小到大的顺序垒前缀和，显然可以用 Exchange Argument 证明。

于是问题变成，\(a\) 把整个时间轴划分成很多段，你现在有一堆点在时间轴上，每个点都能往后移，并且每个点都能覆盖到所在段的末尾，求覆盖的最长总长度。

我们考虑从后往前扫，每遇到一个点可以往后管一个区间，那么我们用一个大根堆维护后面所有可管区间的代价。

首先我们发现，每一段里面可能有很多点，但是只有第一个是有用的（因为它产生的覆盖严格包含后面的点产生的覆盖），后面的点可以当成没用的点拿去管后面最大的一些区间。但是这里可能会有一个问题，如果把第一个点拿走了，会不会把后面的点重新放回来产生更大的贡献呢？（伏笔）

我们考虑第一个点挪或者不挪。如果后面能有一个更好的，那么就挪过去，然后把这个位置空出来的代价放进堆里。因为这一步是更优的，所以这一步放过去肯定不会反悔，只会多出这个空段一个决策。此时可以证明，被挪走的后面的点不可能放回来造成更大的贡献，因为它们的后移造成了比这整段还长的贡献（因为第一个点挪到后面去了，证明大根堆前面出去的点都比这段的长度大）。

如果后面的不够好，就先暂时把它留在这里，往堆里面插入弄个点过来占这段然后这个点挪走到最好的位置的代价，显然是很正确的。

特别地，如果这一段里面没有点，就直接扔进堆里面表示一个决策。

SA Cup T3 错过的追逐

好题。

首先看完题立马反应到欧拉回路，立马反应到当前弧优化，灵感思考一番可以得到一个很正确的做法：

• 从一个点开始 DFS。
  • 如果 DFS 到没有经过的点，那么接着走。
  • 如果 DFS 到来的点（即 DFS 树上的父亲节点），那么可以记录是怎么过来的，走回来即可。
  • 如果 DFS 到返祖边，那么走到返祖边，显然按照 DFS 性质这条边肯定没有走过，所以我们直接走回那个点接着正常做，直到再次遇到这条边，就回来继续刚刚的过程。

做法正确性比较显然，而且一算可以发现返祖边走了恰好两次，树边走了恰好四次，在题目限制内。

麻烦的是实现。如果我们直接用传统 DFS 的话想继续过程 return 回去会很麻烦（因为调用栈中间卡着很多状态），所以我们魔改 DFS，我们把它改成移动到一个点上，这样的改变只有回溯的时候也需要写函数而不能直接 return，并且每次只能往一个儿子里面走，走回来在另一个过程里面接着走。用当前弧优化当全局指针避免走重就行。

很厉害的技巧。